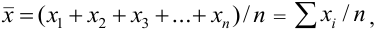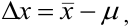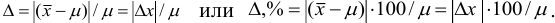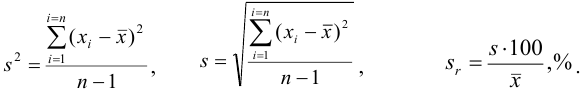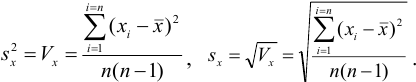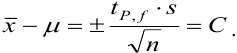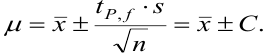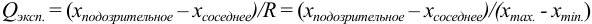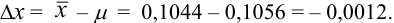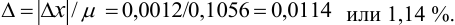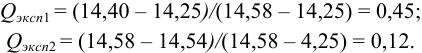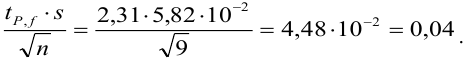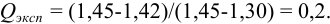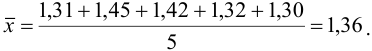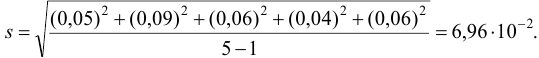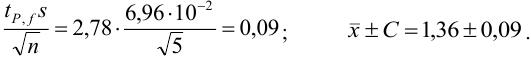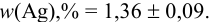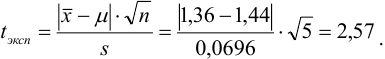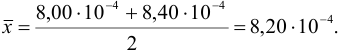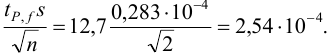Абсолютная и относительная ошибки анализа
В
любом анализе всегда неизбежны ошибки.
Различают абсолютную и относительную
ошибки анализа. Разница в абсолютных
цифрах между истинным (или наиболее
достоверным) значением определяемой
величины н полученный результат
называется абсолютной ошибкой. При
определении содержания бария в BaCl2•2H20
она равна;
56,24 – 56,11 = +0,13
Относительная
ошибка представляет собой отношение
абсолютной ошибки к истинному (или
среднему) значению определяемой величины,
выраженное в процентах:
При гравиметрических
определениях относительная ошибка
допускается обычно не более ± 0,2 — ±0,4%.
2.3.2 Лабораторная работа № 7. Определение содержания бария в BaCl2•2h20. Принцип определения.
В основе
определения содержания бария в указанном
кристаллогидрате лежит реакция,
выражаемая уравнением:
Образующийся
осадок сульфата бария малорастворим в
воде
(ПРва50 == 1,08·10-10).
Для понижения его растворимости осаждение
ведут серной кислотой при некотором
избытке одноименного с ним иона S042-
(по сравнению с эквивалентным количеством).
Серная кислота может частично
адсорбироваться осадком, но при его
прокаливании она улетучивается. Сульфат
бария имеет ярко выраженную склонность
к образованию довольно мелких кристаллов,
легко проходящих при фильтровании,
через поры фильтровальной бумаги.
Осаждение нужно вести при условиях,
благоприятствующих образованию
крупнокристалличеекого осадка BaS04.
Собранный, на фильтре осадок (отфильтрованный
и промытый.) вместе с воронкой помещается
в сушильный шкаф для высушивания. Затем
фильтр с осадком помещают в тигель и
прокаливают в муфельной печи. После
охлаждения тигля с веществом в эксикаторе
приступают к взвешиванию. Затем производят
вычисления.
Оборудование:
технохимические и аналитические весы,
разновес, бюкс, стаканы (емкость 200 мл)
.стеклянная палочка (с резиновым
наконечником), аналитическая: воронка,
металлический штатив с кольцом, беззольные
фильтры («синяя лента»), промывалка,
ножницы, тигель, сушильный шкаф, муфельная
печь (или горелка), эксикатор, тигельные
щипцы, набор ареометров (денситометров),
мерные цилиндры (или бюретки), водяная
баня, часовое стекло, асбестовая сетка,
фарфоровый треугольник, пробирки.
Реактивы:
кристаллогидрат BaCl2•2H20,
2 н. H2S04,
промывная жидкость (серная кислота или
нитрат аммония), дистиллированная вода,
2 н. НСl,
0,02 н. AgNO3.
Ход
определения
1.
Взятие навески
и ее растворение.
На аналитических весах взвешивают бюкс
и записывают его массу в журнал. На
техно-химических весах отвешивают (на
листе чистой бумаги) 0,4—0,5 г BaCl2•2H20,
пересыпают вещество в бюкс и взвешивают
на аналитических весах, записав его
массу (вместе с массой пустого бюкса).
Вычисляют массу взятого для анализа
вещества. Навеску количественно переносят
в химический стакан (емкость 200 мл) и
растворяют в 100 мл дистиллированной
воды. После прибавления в полученный
раствор 3—5 мл 2 н. соляной кислоты (для
растворения части центров кристаллизации
и предупреждения образования BaS04
в коллоидном — состоянии), анализируемую
систему закрывают часовым стеклом и
нагревают почти до кипения.
2.
Приготовление
раствора осадителя.
Вычисляют количество 2 н. раствора H2SO4,
требующееся для осаждения ионов бария,
содержащихся в анализируемом образце,
полученном при растворении в воде
навески. При анализе берут полуторное
ее количество (расчет см. выше). Найденное
количество 2н. H2SO4
отмеривают и переносят в другой (чистый)
химический стакан и разбавляют взятую
серную кислоту дистиллированной водой
(примерно до 40 мл). Содержимое второго
стакана нагревают почти до кипения.
3.
Осаждение.
К горячему раствору хлорида бария, при
помешивании стеклянной палочкой,
приливают по каплям (по стеклянной
палочке) нагретый раствор серной кислоты.
При перемешивании нужно стараться не
касаться стеклянной палочкой стенок и
дна стакана, чтобы избежать прилипания
осадка к стеклу.
Перед
концом осаждения оставить несколько
мл раствора серной кислоты (для дальнейшей
проверки на полноту осаждения ионов
Ва2+).
Стакан
с осадком (палочка остается в стакане;
резиновый наконечник ее направлен
вверх) тотчас же помещают на 2—3-часа на
кипящую водяную баню, чтобы сульфат
бария мог осесть на дно стакана и
получился прозрачный раствор. Затем
проверяют полноту осаждения. К прозрачному
маточному раствору по стеклянной палочке
осторожно приливают 1—2 капли оставленной
серной кислоты. Если раствор останется
прозрачным, то осаждение считается
полным. Помутнение раствора укажет «на
то, что ионы бария осаждены не полностью
и нужно прилить к раствору с осадком
еще 2—3 мл оставшейся серной кислоты.
После отстаивания раствора еще раз
провести пробу на полноту осаждения. В
случае повторного помутнения раствора,
вероятно, расчет количества осадителя
проведен неверно и его следует проверить,
внося соответствующие изменения в
количество взятого осадителя. Часовое
стекло ополаскивается
над стаканом
с осадком.
Убедившись в
полноте осаждения, стакан с осадком
(стеклянная палочка не вынимается)
накрывают чистой бумагой (с указанием
фамилии студента) и оставляют до
следующего занятия. Медленное охлаждение
благоприятствует образованию
крупнокристаллического осадка, который
после созревания отфильтровывают.
4. Фильтрование
и промывание осадка.ОсадокBaS04отфильтровывают с помощью беззольного
фильтра («синяя лента»). Такой фильтр
вкладывают в аналитическую воронку,
расправляют и смачивают дистиллированной
водой. Воронку помещают в кольцо штатива.
Когда на фильтр по палочке будет слита
с осадка почти вся жидкость, сульфат
бария декантируют, приливая в стакан
по 10 мл примерно 0,1% серной кислоты (3—4
раза), каждый раз возможно полнее сливая»
жидкость с осадка на фильтр.
Соблюдая
правила предосторожности, осадок
количественно переносят на фильтр,
пользуясь промывалкой, заполненной
промывной жидкостью. Осадок промывается
на фильтре до тех. пор, пока в последних
порциях фильтрата при помощи нитрата
серебра (реакция проводится в пробирке)
нельзя будет обнаружить наличие
хлорид-ионов». Часто при окончательном
промываний осадка на фильтре используют
1% раствор нитрата аммония (3 мл 33% NH4NO3
в 100 мл дистиллированной воды), который
при прокаливании улетучивается и не
загрязняет осадка. Эта добавка препятствует
пептизации и в некоторой степени
способствует вытеснению с осадка и
фильтра серной кислоты, которая придает
фильтру хрупкость в процессе его
высушивания. Осадок, находящийся в
хрупком фильтре, может быть легко потерян
при перенесении его в тигель.
5.
Вылушивание
и прокаливание осадка.
По окончании промывания воронку с
осадком (BaS04)
накрывают чистым листом бумаги, загибают
края,
чтобы она не падала, и ставят в: сушильный
шкаф» предназначенный для сушки веществ,
находящихся на фильтре, в воронке. Не
следует высушивание доводить до конца,
если осадок далее будут прокаливать. В
этом случае фильтр нужно оставлять
слегка влажным, так как он (совершённо
сухой) при завертывании в него осадка
ломается, Свернутый фильтр вместе с
осадком аккуратно помещают в предварительно
вымытый, прокаленный (до постоянной
массы) и взвешенный фарфоровый тигель.
Прокаливание последнего ведут при тех
же условиях, при которых будет прокаливаться
осадок BaS04.
Поместив содержимое в тигель, приступают
к осторожному обугливанию фильтра.
Прокаливание проводится при температуре
600 — 800°C
в течение 40 минут (до полного, озоления
фильтра). Прокаливание при более высокой
температуре может привести к разложению
частиц осадка и к ошибке анализа (без
применения соответствующих операций):
По окончании
прокаливания горячий тигель щипцами
осторожно переносят в эксикатор, где
он охлаждается до комнатной температуры,
а затем взвешивается. Прокаливание
осадка и его взвешивание повторяют до
тех пор, пока не получат в результате
взвешивания разницу не более 0,0002 г. Если
масса тигля с осадком (при дальнейшем
его прокаливании) практически не
меняется, производят вычисления.
6.
Вычисление результатов анализа.
а)
По массе осадка и формуле вещества
вычислите количество бария в BaSO4.
б)
Найдите истинное содержание бария в
BaCl2•2H20.
в) Вычислите
абсолютную и относительную ошибки
анализа и сделайте вывод о точности
определения.
Опредёление
влажности и кристаллизационной воды в
кристаллогидратах
Принцип
определения.
Определение влажности веществ и
кристаллизационной воды в кристаллогидратах
(например, в BaCl2•2H20)
основано да нахождении уменьшения массы
исходной навески после высушивания (до
постоянной массы) в сушильном шкафу при
определенной температуре.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Разница между абсолютной ошибкой и относительной ошибкой
Автор:
Charles Brown
Дата создания:
9 Февраль 2021
Дата обновления:
2 Июнь 2023
Содержание
- Ключевое различие — абсолютная ошибка против относительной ошибки
- Что такое абсолютная ошибка?
- Что такое относительная ошибка?
- В чем разница между абсолютной ошибкой и относительной ошибкой?
-
Ключевое различие — абсолютная ошибка против относительной ошибки
Абсолютная ошибка и относительная ошибка — это два способа указания ошибок в экспериментальных измерениях, хотя существует разница между абсолютной ошибкой и относительной ошибкой на основе их расчета. Большинство измерений в научных экспериментах содержат ошибки из-за инструментальных ошибок и ошибок человека. В некоторых случаях для конкретного измерительного прибора существует заранее определенное постоянное значение абсолютной погрешности. (Наименьшее показание. Например: — линейка = +/- 1 мм.) Это разница между истинным значением и экспериментальным значением. Однако относительная ошибка варьируется в зависимости от экспериментального значения и абсолютной ошибки. Он определяется отношением абсолютной ошибки к экспериментальному значению. Таким образом ключевое отличие между абсолютной ошибкой и относительной ошибкой, абсолютная ошибкаэтовеличина разницы между точным значением и приближением в то время как Относительная погрешность рассчитывается путем деления абсолютной погрешности на величину точного значения.
Что такое абсолютная ошибка?
Абсолютная ошибка — это показатель неопределенности измерения. Другими словами, он измеряет, в какой степени истинное значение может отличаться от экспериментального. Абсолютная погрешность выражается в тех же единицах, что и измерения.
Пример: Допустим, мы хотим измерить длину карандаша с помощью линейки с миллиметровыми отметками. Мы можем измерить его длину с точностью до миллиметра. Если вы получите значение 125 мм, оно будет выражено как 125 +/- 1 мм. Абсолютная погрешность составляет +/- 1 мм.
Что такое относительная ошибка?
Относительная ошибка зависит от двух переменных; абсолютная погрешность и экспериментальное значение измерения. Следовательно, эти два параметра должны быть известны для расчета относительной ошибки. Относительная ошибка вычисляется как отношение абсолютной ошибки к экспериментальному значению. Выражается в процентах или дробях; так что в нем нет единиц.
Относительная ошибка интегрирования Монте-Карло для вычисления числа пи
В чем разница между абсолютной ошибкой и относительной ошибкой?
Определение абсолютной ошибки и относительной ошибки
Абсолютная ошибка:
Абсолютная ошибка — это значение Δx (+ или — значение), где x — переменная; это физическая погрешность измерения. Он также известен как фактическая ошибка измерения.
Другими словами, это разница между истинным значением и экспериментальным значением.
Абсолютная ошибка = фактическое значение — измеренное значение
Относительная ошибка:
Относительная ошибка — это отношение абсолютной ошибки (Δx) к измеренному значению (x). Он выражается либо в процентах (процентная погрешность), либо в виде дроби (дробная погрешность).
Единицы и расчет абсолютной погрешности и относительной погрешности
Единицы
Абсолютная ошибка:
Он имеет те же единицы измерения, что и измеренное значение. Например, если вы измеряете длину книги в сантиметрах (см), абсолютная ошибка также будет иметь те же единицы.
Относительная ошибка:
Относительная погрешность может быть выражена в виде дроби или процента. Однако у обоих нет единицы в стоимости.
Расчет ошибок
Пример 1:Фактическая длина земли составляет 500 футов. Измерительный прибор показывает, что длина составляет 508 футов.
Абсолютная ошибка:
Абсолютная ошибка = [Фактическое значение — измеренное значение] = [508-500] футов = 8 футов
Относительная ошибка:
В процентах:
В виде дроби:
Пример 2:
Студент хотел измерить высоту стены в комнате. Он измерил значение с помощью метровой линейки (с точностью до миллиметра), оно составило 3,215 м.
Абсолютная ошибка:
Абсолютная погрешность = +/- 1 мм = +/- 0,001 м (Наименьшее значение, которое можно прочитать с помощью линейки)
Относительная ошибка:
Относительная погрешность = Абсолютная погрешность ÷ Экспериментальное значение = 0,001 м ÷ 3,215 м * 100 = 0,0003%
УДК 517
Николаева И.В. студент магистратуры 1 курс, институт «Экономики и управления» Самарский национальный исследовательский университет имени академика С.П.Королева
Россия, г. Самара ОСОБЕННОСТИ ПРИМЕНЕНИЯ АБСОЛЮТНОЙ И ОТНОСИТЕЛЬНОЙ ОШИБКИ АППРОКСИМАЦИИ В РЕГРЕССИОННОМ АНАЛИЗЕ Аннотация: Статья посвящена абсолютной, и относительной ошибкам аппроксимации для линейных регрессионных моделей, как наиболее часто встречающихся на практике.
Ключевые слова: регрессионный анализ, аппроксимация, относительная ошибка, абсолютная ошибка.
Nikolaeva I. V. student magistracy 1 course, Institute «Economy and management» Samara national research University named after academician S. P.
Korolev Russia, Samara APPLICATION FEATURES ABSOLUTE AND RELATIVE APPROXIMATION ERRORS IN REGRESSION ANALYSIS Abstract: the Article deals with both absolute and relative approximation errors for linear regression models, as the most common in practice.
Key words: regression analysis, approximation, relative error, absolute
error.
Разработка эконометрических моделей является целью эконометрического анализа, позволяющая спрогнозировать тенденции развития экономических процессов для принятия обоснованных решений. Эконометрические модели позволяют выявить особенности функционирования объекта и благодаря этому предсказать будущее его поведение при изменении какого-либо параметра. Для любого субъекта возможность прогнозирования ситуации значит получение наилучших результатов, избежание потерь, минимизация рисков. Построение эконометрических моделей с целью анализа и прогнозирования экономических процессов является важной задачей при проведении исследования любого уровня. Однако проблема оценки качества полученной модели является ключевой в моделировании.
Оценка значимости как уравнения в целом, так и отдельных его параметров проводится после того как уравнение регрессии найдено. Значимость уравнения регрессии — это установление соответствия математической модели, выражающей зависимость между переменными, эмпирическим данным и определение достаточного количества включенных
в уравнение объясняющих переменных для описания зависимой переменной. При подборе уравнения тренда, значение ошибки аппроксимации может служить для выбора наиболее подходящего уравнения. Аппроксимация результатов наблюдений может идти по разным моделям, но наилучшей аппроксимацией является та, в которой минимально отклонение между моделью и реальными данными в относительных значениях.
Фактические значения результативного признака отличаются от теоретических значений, рассчитанных по уравнению регрессии, т. е. у и ух. Чем меньше эти отличия, тем ближе теоретические значения к эмпирическим данным, тем лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака (у — ух) по каждому наблюдению представляет собой ошибку аппроксимации. Их число соответствует объему совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Отклонения (у — ух) несравнимы между собой, исключая величину, равную нулю. Для сравнения используются величины отклонений, выраженные в процентах к фактическим значениям.
Отклонения (у — ух) можно рассматривать как абсолютную ошибку аппроксимации. Поскольку (у — ух) может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю. Относительная ошибка аппроксимации рассчитывается по формуле:
У-Ух
* 100 (1)
У
Чем ближе измеренное значение к истинному значению, тем точнее измерение. Если экспериментальное значение меньше реального, то абсолютная ошибка отрицательна, а если экспериментальное значение больше реального, то абсолютная ошибка положительна.
Таким образом, величина отклонения теоретического значения результативного признака от фактического значения, взятая по модулю, представляет собой абсолютную ошибку аппроксимации. А величина, равная отношению абсолютной ошибки к фактическим значениям результативного признака, выраженная в процентах, является относительной ошибкой аппроксимации.
Для иллюстрации приведены данные опроса шести семей (в которой два работающих взрослых и один ребенок) г.Самара по связи расходов на продукты питания с уровнем доходов этих семей.
_Таблица 1 — Данные опроса
Расходы семьи на продукты питания, y, руб/месяц Доходы семьи, x, руб/месяц
8000 21000
18000 50000
10000 23000
15000 40000
11000 27000
12000 30000
На основе поля корреляции можно сделать предположение, что связь между доходами и расходами на продукты питания — линейная.
б
у
я р
К
и ь м 64 и К т
е Н
с и
ы С
д о ы
х
с гг1 у
Рн до
р
с
20000 15000 10000 5000 0
10000 20000 30000 40000 Доходы семьи, руб.
50000
60000
Рисунок 2 — Поле корреляции по данным опроса
Предположительно зависимость является линейной, поэтому получены следующие параметры линейного уравнения парной регрессии.
Ь = 0,322112
а = 2079,451
А уравнение парной регрессии для представленных данных будет следующее:
% = 2079,451 + 0,322112 * х
Рисунок 3 — Поле корреляции и линия тренда
Из уравнения можно сделать вывод, что с увеличением доходов семьи на 1000 рублей, расходы на питание увеличиваются на 322,112 рублей.
0
Таблица 2 — Расчет абсолютной, относительной, средней ошибки _аппроксимации
х у х*у X2 У2 ух у-ух |у-ух 1 /у*100
1 21000 8000 168000000 441000000 64000000 8843,8 843,8 10,5
2 50000 18000 900000000 2500000000 324000000 18185,0 185,0 1,0
3 23000 10000 230000000 529000000 100000000 9488,0 512,0 5,1
4 40000 15000 600000000 1600000000 225000000 14963,9 36,1 0,2
5 27000 11000 297000000 729000000 121000000 10776,5 223,5 2,0
6 30000 12000 360000000 900000000 144000000 11742,8 257,2 2,1
Итого 191000 74000 2555000000 6699000000 978000000 74000,0 — 21,1
Ср. знач 31833,3 12333,3 425833333,3 1116500000 163000000 12333,3 — 3,5
Таким образом, средняя ошибка аппроксимации А = 3,5%, что говорит о хорошем качестве уравнения регрессии, т.е. свидетельствует о хорошем подборе модели к исходным данным и показывает, что линия регрессии хорошо приближает исходные данные.
На основе проведенного расчета можно сделать следующие выводы. Чем ближе измеренное значение к реальному значению, тем точнее измерение. Абсолютная ошибка является недостаточно показательной. Поэтому нагляднее точность измерения будет характеризоваться отношением абсолютной ошибки к полученному значению измеренной величины, а именно относительная ошибка. Если в ряде данных имеются значения у, близкие к нулю, то значение абсолютной ошибки аппроксимации также становится чрезмерно завышенным вне зависимости от адекватности построенной модели. Кроме того, если значение ух имеет значение равное нулю или близко к нулю, то, относительная ошибка аппроксимации перестает учитывать разницу между фактическим и расчетным значениями — под знаком суммы получается единица. А также, если фактические данные ряда имеют очень большие значения, то есть измеряются в тысячах единиц, то знаменатель становится очень большим, в результате чего средняя ошибка аппроксимации существенно занижается, вне зависимости от качества построенной модели.
Таким образом, можно сделать вывод, что объективно оценить качество модели только по абсолютной, относительной ошибкам аппроксимации не представляется возможным, так как абсолютная ошибка зависит от выбора масштаба измерения, а относительная ошибка завышает вклад ошибки вблизи нулевого значения.
Использованные источники: 1.Эконометрика : учебник для бакалавриата и магистратуры /И. И. Елисеева [и др.] ; под ред. И. И. Елисеевой. — М. : Издательство Юрайт, 2015. — 449 с. — Серия : Бакалавр и магистр. Академический курс.
2.О.В. Любимцев, О.Л. Любимцева, Линейные регрессионные модели в эконометрике. Методическое пособие. Нижний Новгород, ННГАСУ, 2016. З.Федеральная служба государственной статистики http://www.gks.ru
УДК 378.1(063)
Овакимян М.А., кандидат экономических наук, доцент кафедра «Государственное и муниципальное управление» Южно-Российский институт управления-филиал РАНХиГС
Россия, г. Ростов-на-Дону Андриасова К.Г. студент магистратуры 2 курс, факультет управления Южно-Российский институт управления-филиал РАНХиГС
Россия, г. Ростов-на-Дону ОЦЕНКА КАДРОВОГО ПОТЕНЦИАЛА ОБРАЗОВАТЕЛЬНОЙ ОРГАНИЗАЦИИ Аннотация: проблема кадрового потенциала в системе высшего образования представляется ключевой. Именно от уровня кадрового потенциала ВУЗа в конечном итоге будет зависеть уровень квалификации, полученный выпускником. Образовательная система является фундаментом развития общества в целом, что актуализирует необходимость определения критериев оценки кадров и формирование системы аттестационных мероприятий в соответствии с требованиями времени.
Основой для повышения эффективности кадрового потенциала ВУЗа является разработка профессиональных стандартов, определяющая уровень компетенций сотрудников. Важно понимать, что оценочная система должна учитывать различные формы оценивания, с учетом специфики ВУЗа.
Ключевые слова: оценка, компетенция, инновация, аттестация, квалификация, подготовка и т.д.
Оvakimyan M.A., Candidate of Economic Sciences, Associate Professor
Public Administration South-Russia Institute of Management RANEPA
Russia, Rostov-on-Don Andriasova K. G. master’s student 2nd year, Faculty Public Administration, South-Russia Institute of Management RANEPA
Russia, Rostov-on-Don ASSESSMENT OF PERSONNEL POTENTIAL OF THE EDUCATIONAL ORGANIZATION Abstract: the problem of human resources in the higher education system seem to be key. It is the level of personnel potential of the University will
Классификация и оценка погрешностей количественного анализа
По способу вычисления различают абсолютную 

Если среднее арифметическое значение 
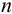
то абсолютную погрешность выражают как
где 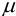
Относительная погрешность может быть выражена в долях или процентах и обычно не имеет знака:
По происхождению погрешности делят на систематические, случайные и промахи (грубые ошибки).
Погрешность определения, обусловленная постоянно действующей причиной, неизменная во всех измерениях, сохраняющая знак от опыта к опыту или закономерно изменяющаяся, называется систематической погрешностью. Погрешность, случайным образом изменяющаяся от опыта к опыту, называется случайной погрешностью. Грубые погрешности или промахи резко искажают результат анализа, вызываются небрежностью и обычно легко обнаруживаются.
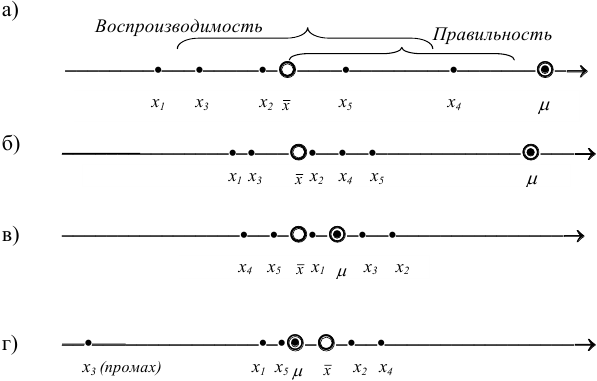
Рис. 9.1. Воспроизводимость и правильность химического анализа. Результаты: а) невоспроизводимы и неправильны; б) воспроизводимы, но неправильны; в) воспроизводимы и правильны; г) воспроизводимы и правильны, но есть промах.
С систематическими погрешностями связана правильность анализа, со случайными погрешностями — воспроизводимость. Правильность и воспроизводимость являются метрологическими характеристиками анализа и входят в понятие «точность анализа».
Воспроизводимость результатов анализа характеризует рассеяние единичных результатов относительно среднего.
Правильность характеризует отклонение полученного результата от истинного и показывает, насколько близка к нулю систематическая погрешность. Систематические погрешности выявляют и устраняют. Если же устранение невозможно, то при постоянном значении систематической погрешности ее учитывают, вводя поправку. Для выявления используют различные приемы и методы, например “введено — найдено”, анализ стандартного образца, “двойной или тройной добавки”.
Оценка случайных погрешностей проводится методами математической статистики. В обычной практике выполняют ограниченное число параллельных измерений п (обычно 3-5), называемое выборочной совокупностью данных или просто выборкой (в отличие от генеральной совокупности — при 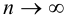
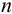
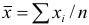
Характеристики случайной погрешности (воспроизводимости) для выборки: выборочная дисперсия 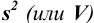
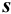
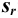
С ними связаны дисперсия среднего 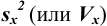
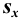
При обработке данных химического анализа определяют границы доверительного интервала 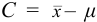
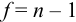
Доверительный интервал (С) — это интервал значений, в котором для данного вида распределения случайных величин (при отсутствии систематических погрешностей), при заданной доверительной вероятности Р и числе степеней свободы 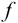
Доверительная вероятность попадания величины внутрь доверительного интервала в химическом анализе принята равной 0,95 или 95 %. Это означает, что в рассчитанный интервал попадут 95 из 100 значений. Коэффициенты 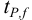
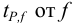
Оценка промахов (выбраковка результатов). Перед обработкой данных методами математической статистики необходимо выявить промахи и исключить их из числа обрабатываемых результатов. Для выявления промахов используют различные критерии, в частности, 

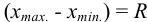
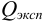
и сравнивают с критическим значением 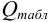
Если 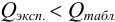
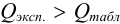

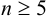
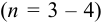
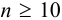
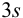
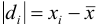
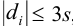
Пример 9.1.
Контрольный раствор соли кальция имеет концентрацию 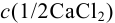
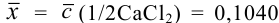
Решение:
Абсолютная погрешность результата:
Относительная погрешность:
Пример 9.2.
При определении содержания аскорбиновой кислоты в пробе картофеля по новой методике пробоподготовки получены следующие результаты (мг/100 г): 14,50; 14,43; 14,54; 14,45; 14,44; 14,52; 14,58; 14,40; 14,25; 14,49. Оцените:
а) наличие грубых погрешностей (промахов);
б) воспроизводимость результатов анализа.
Решение:
а) наличие промахов оценим по 

Из табл. 9 приложения при 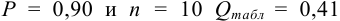
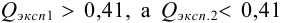
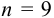
б) после исключения промаха найдем среднее и характеристики воспроизводимости: дисперсию 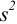
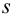
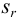
Пример 9.3.
Используя условия примера 9.2 и считая, что содержание аскорбиновой кислоты для той же пробы картофеля, определенное по стандартной методике составляет 14,58 мг/100 г, рассчитайте доверительный интервал и установите, свидетельствуют ли полученные результаты о наличии систематической погрешности при работе по новой методике?
Решение:
Для расчета доверительного интервала при числе степеней свободы 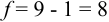
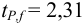
Находим полуширину доверительного интервала, оставляя значащие цифры:
Таким образом, среднее содержание аскорбиновой кислоты лежит в границах
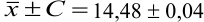
Пример 9.4.
При анализе стандартного образца, содержащего 1,44 % 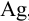
Решение:
Проверим наличие грубых погрешностей по 

Для 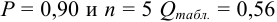

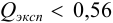
Находим среднее значение из пяти определений:
Вычисляем стандартное отклонение:
По табл. 8 приложения для 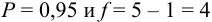
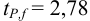
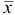
Результат представляем в виде:
Наличие систематической погрешности можно выявить, как в предыдущем примере, проверяя попадает ли истинное значение содержания серебра в доверительный интервал. В данном случае для 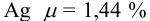
Ответить на вопрос задачи о присутствии систематической погрешности можно, используя критерий Стьюдента и сравнивая вычисленное значение 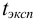
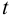
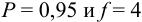
Поскольку 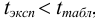
Пример 9.5.
При определении ванадия были получены результаты: 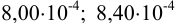
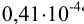
Решение:
Находим среднее значение:
Вычислим стандартное отклонение:
По табл. 8 приложения находим 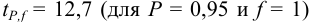
Требуется же получить доверительный интервал с полушириной 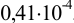
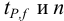
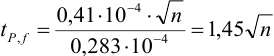
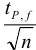
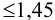
При 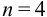
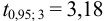
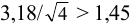
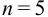
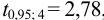
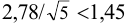
Таким образом, для сужения границ доверительного интервала до 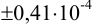
Эти примеры взяты со страницы примеров решения задач по аналитической химии:
Решение задач по аналитической химии
Возможны вам будут полезны эти страницы: