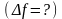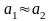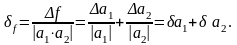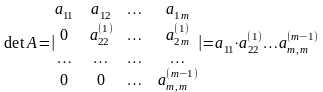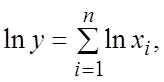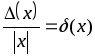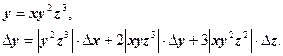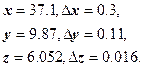Абсолютная и относительная ошибка функции

Вычисления
с конечной точностью и их особенности.
Абсолютная (предельная абсолютная) и
относительная (предельная относительная)
погрешности. Источники возникновения
погрешностей в вычислительной математике.
Погрешности арифметических операций
и погрешность вычисления функции.

Любое
приближенное вычисление связано с
ошибкой (погрешностью).

Виды
ошибок:

Погрешность
математической модели, связанная с
неполными знаниями о процессе.
Погрешность
упрощения модели.
Погрешность,
связанная с приближенным характером
начальных данных.
Погрешность
приближения.

Первые
две погрешности относятся к систематическим,
а две последние – к статистическим.

Абсолютные и относительные погрешности.

Абсолютная
(предельная) погрешность определяет
интервал, в котором лежит точное значение
величины.

Пусть
А – точное значение величины (оно нам
неизвестно). а – приближенное
значение величины (известно). За абсолютную
погрешность Δ принимается минимальное
число Δа, удовлетворяющее условию:
Δ≥|А-а|.

При
статических измерениях погрешность Δа
задается с определенной достоверностью,
т.е. вероятность события |А-а|≤ Δа больше
определенной величины γ: P(|A-a|≤
Δa)≥ γ≤1

Перепишем
определение: а- Δа≤А≤а+ Δа; точное
значение А лежит в заданном интервале.

Для
оценки качества измерений вводится
относительная погрешность

Заданные
величины Δа и δа позволяют записать
точное значение А в символическом виде:
А=а(1± δа)

Погрешность функций.

Пусть
дана функция

от n приближенных
значений

,
погрешности которых известны. Требуется
определить погрешность функции

.

,
где

—
абсолютная погрешность приближенной
величины

.
Если

,
то разность, стоящую в формуле можно
оценить в линейном приближении:

Отсюда
следует оценка погрешности:

Погрешность простейших функций двух переменных

Погрешность
суммы:

Погрешность
разности:

При

качество измерений разности ухудшается.

Замечание:
Абсолютная
погрешность суммы и разности n
приближенных
величин равна сумме их абсолютных
погрешностей.

Погрешность
произведения:

То
есть предпочтительней сначала найти
относительную погрешность, а затем
искать абсолютную:

Замечания:

Относительная
погрешность степени есть произведение
модуля показателя на относительную
погрешность основания степени:
.
Относительная
погрешность произведения n
сомножителей приближенных величин
равна сумме относительных погрешностей
сомножителей:

.

Погрешность
частного:

Все
замечания сделанные для произведения
справедливы и в этом случае.

Решение
систем линейных уравнений методом
Гаусса. Метод исключения Гаусса без
выбора ведущего элемента, возможность
роста погрешности. Схемы с частичным
и полным выбором ведущего элемента.
Количество
операций для рассматриваемых алгоритмов.

Метод
Гаусса (Метод исключений)

Численное
решение систем вида:

(1)

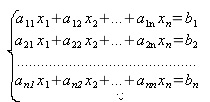
или
Ax=b методом Гаусса заключается в
последовательном исключении неизвестных.
Система (1) поэтапно приводится к
треугольному виду. Сначала исключается
x1 из 2-го, 3-го, …, n-го уравнений, для этого
необходимо сложить уравнения 2,3,…,n с
первым уравнением, умноженным на
-a21/a11, -a31/a11,…, -an1/a11 соответственно .

(2)

Потом
x2 из 3-го,…, n-го умножением второго
уравнения на -a¹32/a¹22, -a¹42/a¹22,…,

-a¹n2/a¹22
и сложением с 3,4,..n уравнениями.

И
дальше по аналогии система приводится
к треугольному виду:

процесс
приведения системы к треугольному виду
называется прямым ходом. Общие фомулы
для прямого хода:

k
=1,…,n – 1; i,j = k+1,…,n .

Для
нахождения решения теперь необходимо
вычислить неизвестные, начиная с n-го
уравнения. Процесс вычисления значений
неизвестных называется обратным ходом.

На
каждом этапе xk находится по формуле

k
= n, n-1, …, 1.

Один
из основных недостатков метода Гаусса
связан с тем, что при его реализации
накапливается вычислительная погрешность.
В книге [ Самарский , Гулин] показано,
что для больших систем порядка m
число действий умножений и делений
близко к

.

Для
того, чтобы уменьшить рост вычислительной
погрешности применяются различные
модификации метода Гаусса. Например,
метод Гаусса с выбором главного элемента
по столбцам, в этом случае на каждом
этапе прямого хода строки матрицы
переставляются таким образом, чтобы
диагональный угловой элемент был
максимальным. При исключении
соответствующего неизвестного из других
строк деление будет производиться на
наибольший из возможных коэффициентов
и следовательно относительная погрешность
будет наименьшей.

Существует
метод Гаусса с выбором главного элемента
по всей матрице. В этом случае переставляются
не только строки, но и столбцы^¹.
Использование модификаций метода Гаусса
приводит к усложнению алгоритма
увеличению числа операций и соответственно
к росту времени счета. Поэтому
целесообразность выбора того или иного
метода определяется непосредственно
программистом^².

Выполняемые
в методе Гаусса преобразования прямого
хода, приведшие матрицу А
системы к треугольному виду позволяют
вычислить определитель матрицы

Метод
Гаусса позволяет найти обратную матрицу.
Для этого необходимо решить матричное
уравнение

где
Е
единичная матрица. Его решение сводится
к решению m
систем

у
вектора

j
–я компонента равна единице, а остальные
компоненты равны нулю.

Метод
Гаусса-Жордана для решения системы
уравнений

Метод
Гаусса-Жордана является еще одной
вариацией метода Гаусса для решений
систем уравнений. Его отличием является
отсутствие обратного хода, но при этом
количество действий, выполняемых для
решения системы увеличивается. Рассмотрим
следующую систему уравнений 3-го порядка:

Первым
этапом производится нормирование
первого уравнения, далее исключается
переменная x1. Отличием является то, что
выражение для xkподставляется во все
уравнения кроме k-го (с ведущим элементом).
Далее действия повторяются и исключается
вторая переменная, а затем и третья.

Нормирование
1-го уравнения, исключение x1,

Нормирование
2-го уравнения, исключение x2

Нормирование
3-го уравнения, исключение x3

Достоинством
метода Гаусса-Жордана является простота
программирования за счет отсутствия
обратного хода.

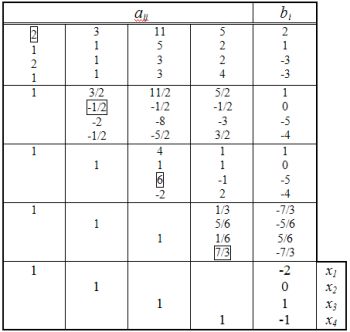
Табличное
представление решения системы уравний
методом Гаусса-Жордана.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Вычисление погрешности функций. Определение допустимой погрешности аргументов по допустимой погрешности функций

Страницы работы

Фрагмент текста работы

б) 0,096835; . б)
0,66385; .

3) а)12,688 ; б)
4,636. 3) а) 6,743; б) 0,543 .

18.4.
ВЫЧИСЛЕНИЕ ПОГРЕШНОСТИ ФУНКЦИЙ

18.4.1. Функции одной переменной. Абсолютная погрешность дифференцируемой
функции , вызываемая достаточно малой погрешностью
аргумента , оценивается величиной

,
(18.12)

Если значения функции положительны, то для относительной погрешности
имеет место оценка

. (18.13)

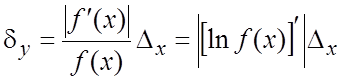
Например, для
тригонометрических функций абсолютные погрешности синуса и косинуса не
превосходят абсолютных погрешностей аргумента:

, . (18.14)

18.4.2. Функции нескольких
переменных. Пусть
задана некоторая функция , от п аргументов
и пусть значения каждого из аргументов , определены с некоторыми погрешностями , i = 1, 2,…, п.
Требуется найти погрешность данной функции.

Для
решения этой задачи будем предполагать, что функция является
дифференцируемой в некоторой области D. Абсолютная погрешность функции
y при заданных абсолютных погрешностях
аргументов равна

. (18.15)

Предполагая, что величины , i = 1, 2,…, п достаточно
малы, можно записать приближенные равенства

(18.16)

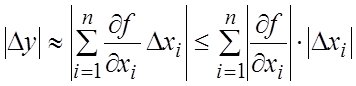
Следовательно, предельная абсолютная
погрешность функции y равна

,
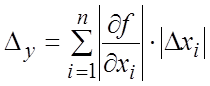
(18.17)

где предельная
абсолютная погрешность аргумента .

Оценка для относительной
погрешности функции получается путем деления обеих частей неравенства (18.15)
на

(18.18)

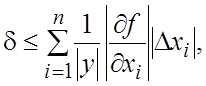
Из формулы (18.18) получаем выражение
для предельной относительной погрешности функции у

(18.19)

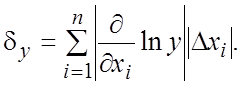
Рассмотрим
отдельные примеры на вычисление погрешностей различных функциональных
соотношений. Будем предполагать, что в каждом примере заданы те или иные
погрешности аргументов.

1. Пусть .
По формуле (18.17) предельная абсолютная погрешность суммы п слагаемых
равна

. (18.20)

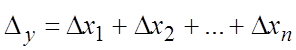
2. Пусть . По
формуле (18.17) предельная абсолютная погрешность разности двух чисел равна

3. Пусть , причем x_i (i=1, 2, …, п) положительны. В соответствии с формулой (18.19)
проведем преобразования с целью получения выражения для предельной
относительной погрешности произведения п сомножителей

4. Пусть 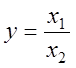. По
формуле (18.19) предельная относительная погрешность частного равна

5. Пусть . Тогда .

6. Пусть .
Следовательно, .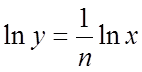

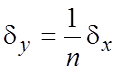
18.5. Определение допустимой погрешности аргументов по допустимой
погрешности функций

Задача определения какими должны быть
погрешности исходных приближений, чтобы полученный результат имел заданную
степень точности, имеет однозначное решение только для функции одной переменной
: если эта функция дифференцируема и , то

.
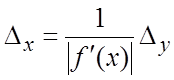
(18.21)

Для функций
нескольких переменных эта задача решается
неоднозначно. Для ее решения необходимо наложить какие-либо условия на
погрешность исходных данных. Если использовать принцип равных влияний, считая что в формуле (18.17) все
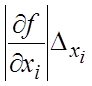
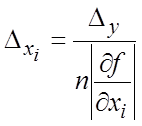
слагаемые равны между собой, получим

.
(18.22)

Пример
8. Даны числа ; . Тогда
. Причем последняя цифра сомнительная.

Пример
9. Найти сумму , где ; ; . Причем
все цифры верные.

Имеем . Предельная абсолютная погрешность суммы . Стало быть, 7.84 < y< 7.87. В результате верными будут
цифры 7.8. Последняя цифра 4 сомнительная. #

Информация о работе

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание — внизу страницы.

Источник

Погрешности значения функции

При
вычислении значения функции
в точке(считаемприближенным значением точного числа)
возникают погрешности – предельная
абсолютнаяи предельная относительная.
Выразим эти погрешности через погрешности
числа(будем полагать, что функциядифференцируема в точке).

Так
как функция
дифференцируема в точке,
то

,
(4.1)

где
мало при малом(иными словами, слагаемымв формуле (4.1) можно пренебречь, еслимало).

Учитывая
равенство (4.1), истинная абсолютная
погрешность
будет оцениваться неравенством
(приближенным)

откуда по определению
предельной абсолютной погрешности

. (4.2)

Итак,
предельная
абсолютная погрешность значения функции
в точке
(– приближенное число) равна произведению
модуля производной этой функции в точкена предельную абсолютную погрешность
числа.

Соответственно
предельная относительная погрешность
вычисляется следующим образом

=. (4.3)

Найдем
с помощью формул (4.2), (4.3) погрешности
значений основных элементарных функций.

Пусть
(– действительное число). Тогда

,
.

В
частности при
:.

Пусть
.
Тогда

,
.

Пусть
.
Тогда

,
.

В
частности, если
,
то.

Аналогично
определяются погрешности значений
других основных элементарных функций
(см. таблицу 4.1).

Таблица 4.1.

№
1
2
3
4
5
6
7
8
9

Пример
4.1. Дана
функция
.
Протабулировать ее на отрезке(считать),
разбив его наравных частей (все расчеты проводить с
4 знаками после запятой). Вычислить
предельные абсолютные, относительные
погрешности значений функции в узлах
табулирования.

Решение:
Протабулировать функцию
на отрезкес постоянным шагомозначает составить таблицу значений,(точкиназываются узлами табулирования), где

. (4.4)

В
нашем случае
,,;
узлы определяются следующим образом:

. (4.5)

Вычислим значения
функции в узлах табулирования (4.5):

Имеем
,;

,
3,3261,

и так далее.

Все
вычисления значения функции в узлах
табулирования заполняем в таблицу 4.2.

Учитывая
формулы (4.2), (4.3), находим погрешности в
узлах (4.5) (при этом число
можно считать точным, а тогда;
в остальных же узлах (4.5),00005)

,
.

Таблица 4.2.

i
0	0	0	1	3	0	0
1	0,6284	0,7927	0,5334	3,3261	4,8678	1,46
2	1,2568	1,2111	0,2846	3,4057	8,0695	2,37
3	1,8852	1,3730	0,1518	3,5248	1,0618	0,3
4	2,5136	1,5854	0,0809	3,6663	1,1724	0,32
5	3,1420	1,7726	0,0432	3,8158	1,1944	0,31

Полиномиальные интерполяции

Весьма
редко удается решить задачу прямыми
аналитическими методами, тем более
реализовать решение в виде вычислительного
алгоритма. Основными требованиями к
алгоритму являются:

—
изменяемость в зависимости от начальных
(исходных) условий, т.е. путь решения
должен быть по возможности универсальным;

—
схематизированность (однозначно должна
быть определена последовательность
действий),

—
рекурсированность – рекурсированный
алгоритм состоит из небольших частей,
которые неоднократно реализуются для
различных наборов значений;

—
решение, реализуемое алгоритмом должно
быть конечным, т.е. должно приводить к
конечному результату за конечное число
шагов. Другими словами, не должно
существовать различного рода расходимостей
(например, часто встречаются т.н.
логарифмические расходимости вида
,
разрывы первого и второго родов, скачки
значений производных и т.д.), которые
могут оказать существенное влияние на
конечный результат. Поэтому реализации
алгоритма непосредственно на ЭВМ должен
предшествовать тщательный анализ задачи
с целью выявления различных особенностей
в поведении исследуемого процесса.

Последнее требование
представляется авторам наиболее важным
с точки зрения достоверности получаемых
результатов вычисления.

Часто
при обработке статистических данных
возникает задача замены аналитического
описания некоторого реального процесса
на другое, более удобное с точки зрения
дальнейших математических преобразований.
Т.е. мы заменяем некоторую функцию f(x)
(известную, неизвестную, частично
известную), другой ψ(x),
полученной в результате некоторых
преобразований. В зависимости от цели
исследования выбирается метод
интерполяции^¹
или экстраполяции — процесс построения
приближенного или аппроксимирующего
многочлена соответственно внутри и вне
промежутка исследования. Так как методики
интерполяции и экстраполяции практически
не отличаются друг от друга, то в
дальнейшем будем ограничиваться
примерами интерполяции. В связи с этим
вышеупомянутую процедуру должен
предварять анализ исходной зависимости
f(x),
а именно:

Способ
и интервал задания функции (аналитический
или табличный);
Оценка степени
гладкости функции, имеется ли возможность
определения производных;
Требования
к интерполирующей функции ψ(x)
(определение ее класса);
Определение
критерия качества интерполяции, иначе
говоря, задание способа оценки погрешности
интерполяции. Необходимо в первую
очередь определить источники погрешностей.
Чаще всего наиболее существенное
влияние оказывают следующие:

— погрешность
исходных данных;

— погрешность
метода;

— погрешность
округления;

Погрешность
исходных данных, как правило, легче
всего поддается оценке и соответствующей
корректировке. Более того, часто удается
получить точную аналитическую формулу
ошибок, исходя из выводов теории
вероятностей и математической статистики.

Так
как вычислительный алгоритм является
рекурсивным, состоящим из целого ряда
операций, то происходит т.н. накопление
погрешностей: погрешности результата
каждого шага оказываются исходными для
следующей операции, поэтому точный
анализ погрешностей оказывается
трудновыполнимым и приходится
ограничиваться доверительными оценками.

Сформулируем
основные положения.

Первое.
Будем рассматривать как таблично, так
и аналитически заданные функции.

Второе.
В основном будем использовать
полиномиальную или кусочно-полиномиальную
интерполяцию, т.е. рассматривать в
качестве аппроксимирующих функций ψ(x)
только многочлены. Данная форма ψ(x)
выглядит в большинстве случаев более
предпочтительной с точки зрения упрощения
дальнейших математических действий
(дифференцирования, интегрирования).
Другие виды приближений (тригонометрическое,
экспоненциальное и пр.) будут применены
в следующих разделах.

Третье.
Построение аппроксимирующего многочлена
и оценку погрешности будем производить
с помощью функционалов

(1)

(2)

соответственно
для непрерывных и дискретных функций.
Оценка погрешности (степени близости
функций f(x)
и ψ(x))
по формулам (1) и (2) смысл среднеквадратичной
погрешности.

Будем
называть вычислительный метод устойчивым,
если для любого
существует такое,
что максимальная погрешность результата
вычислений меньшепри максимальной погрешности исходных
данных меньше.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Абсолютная погрешность дифференцируемой функции y = f(x), вызываемая достаточно малой погрешностью аргумента Dx, оценивается величиной :.

Если значения функции f(x) положительны, то для относительной погрешности имеет место оценка:

Пример 1

Абсолютные погрешности синуса и косинуса находится по формулам:

D sin x = |cos x|×Dx,

D cos x = |sin x|×Dx, где x изменяется в радианах.

Погрешность вычисления значения функции нескольких переменных (общая формула для погрешности)

Абсолютная погрешность дифференцируемой функции y = f(x₁, x₂, x₃, …, x_n), вызываемая достаточно малыми погрешностями Dx₁, Dx₂,…,Dx_n аргументов x₁, x₂, x₃,…,x_n, оценивается величиной:

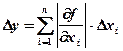
Пример 2

Если значения функции положительны, то для относительной погрешности имеет место оценка:

Пример 3

Вычислить значение функции f, абсолютную и относительную погрешности вычисления f, если

Сначала найдем относительную погрешность вычисления значения f, а затем абсолютную погрешность. Функция f положительна и дифференцируема, поэтому воспользуемся формулой:

; ;

;

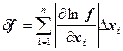
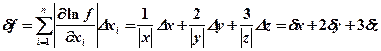
Найдем относительные погрешности аргументов:

; .

Относительная погрешность является величиной порядка 1 %, следовательно, значение f содержит 2 верные значащие цифры. Следовательно, в записи f нужно указать три значащие цифры, две из которых будут верными и одна сомнительная. Вычислим xy²z³ = 801133.57, оставляя три значащие цифры, получим: f = 801*10³. Зная значение f и её относительную погрешность, найдем абсолютную погрешность:

Основная задача теории погрешности заключается в следующем: с какой точностью можно найти значение функции Y=f(X1*, x2*,…, xn*), если аргументы XI* Известны с некоторой точностью. И обратная задача: с какой точностью надо задать значения аргументов функции, чтобы погрешность функции не превосходила заданной величины? Решение таких задач опираются на теорему Лагранжа, согласно которой предельная абсолютная погрешность функции равна произведению абсолютной величины ее производной на предельную абсолютную погрешность аргумента D(F*)=|F ’|D(X*). Если задана дифференцируемая функция Y= f(X1, x2,…, xn) и ее приближенное значение Y*= f(X1*, x2*,…, xn*), где Xi — Точные значения аргументов функции, а Xi* – приближенные к ним, и пусть D(Xi*) (I=1,2,…,n) абсолютные погрешности аргументов функции.

Определение. Предельной абсолютной погрешностью функции А(Y*) называют наилучшую при имеющейся информации оценку погрешности величины Y*= f(X1*+D(X1*), x2+D(X2*) , …, xn+D(Xn*) ),

Т. е. А(Y*)=Sup| F(X1, X2,…, Xn)- F(X1*, X2*,…, Xn*)|.

Линейная оценка погрешности функции записывается в виде:

Разделив обе части неравенства на y*, будем иметь оценку для Предельной относительной погрешности функции D (Y*):

=D(Y*).

< Предыдущая		Следующая >

Загрузить PDF

Абсолютная ошибка – это разность между измеренным значением и фактическим значением.^[1] Эта ошибка характеризует точность измерений. Если вам известны фактическое и измеренное значения, можно с легкостью вычислить абсолютную ошибку. Но иногда фактическое значение не дано, поэтому в качестве абсолютной ошибки пользуются максимально возможной ошибкой.^[2] Если даны фактическое значение и относительная ошибка, можно вычислить абсолютную ошибку.

1

Запишите формулу для вычисления абсолютной ошибки. Формула: $Delta x=x_{{0}}-x$ , где – абсолютная ошибка (разность между измеренным и фактическим значениями), $x_{{0}}$ – измеренное значение, – фактическое значение.^[3]
2
Подставьте в формулу фактическое значение. Фактическое значение должно быть дано; в противном случае используйте принятое опорное значение. Фактическое значение подставьте вместо .
- Например, нужно измерить длину футбольного поля. Фактическая длина (принятая опорная длина) футбольного поля равна 105 м (именно такое значение рекомендуется FIFA). Таким образом, фактическое значение равно 105 м: $Delta x=x_{{0}}-105$ .
3
Подставьте в формулу измеренное значение. Оно будет дано; в противном случае измерьте величину (длину или ширину и так далее). Измеренное значение подставьте вместо $x_{0}$ .
- Например, вы измерили длину футбольного поля и получили значение 104 м. Таким образом, измеренное значение равно 104 м: .
4
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».^[4] Так вы вычислите абсолютную ошибку.
- В нашем примере: , то есть абсолютная ошибка измерения равна 1 м.
Реклама

1

Запишите формулу для вычисления относительной ошибки. Формула: $delta x={frac {x_{{0}}-x}{x}}$ , где – относительная ошибка (отношение абсолютной ошибки к фактическому значению), $x_{{0}}$ – измеренное значение, – фактическое значение.^[5]
2
Подставьте в формулу относительную ошибку. Скорее всего, она будет дана в виде десятичной дроби. Относительную ошибку подставьте вместо .
- Например, если относительная ошибка равна 0,02, формула запишется так: $0,02={frac {x_{{0}}-x}{x}}$ .
3
Подставьте в формулу фактическое значение. Оно будет дано. Фактическое значение подставьте вместо .
- Например, если фактическое значение равно 105 м, формула запишется так: $0,02={frac {x_{{0}}-105}{105}}$ .
4

Умножьте обе стороны уравнения на фактическое значение. Так вы избавитесь от дроби.
5

Прибавьте фактическое значение к каждой стороне уравнения. Так вы найдете $x_{{0}}$ , то есть измеренное значение.
6
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».^[6] Так вы вычислите абсолютную ошибку.
- Например, если измеренное значение равно 107,1 м, а фактическое значение равно 105 м, вычисления запишутся так: . Таким образом, абсолютная ошибка равна 2,1 м.
Реклама

1
Определите единицу измерения. То есть выясните, было ли значение измерено с точностью до сантиметра, метра и так далее. Возможно, эта информация будет дана (например, «длина поля измерена с точностью до метра»). Чтобы определить единицу измерения, посмотрите на то, как округлено данное значение.^[7]
- Например, если измеренная длина поля равна 106 м, значение было округлено до метров. Таким образом, единица измерения равна 1 м.
2
3
Используйте максимально возможную ошибку в качестве абсолютной ошибки.^[9] Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».^[10] Так вы вычислите абсолютную ошибку.
- Например, если измеренная длина поля равна м, то есть абсолютная ошибка равна 0,5 м.
Реклама