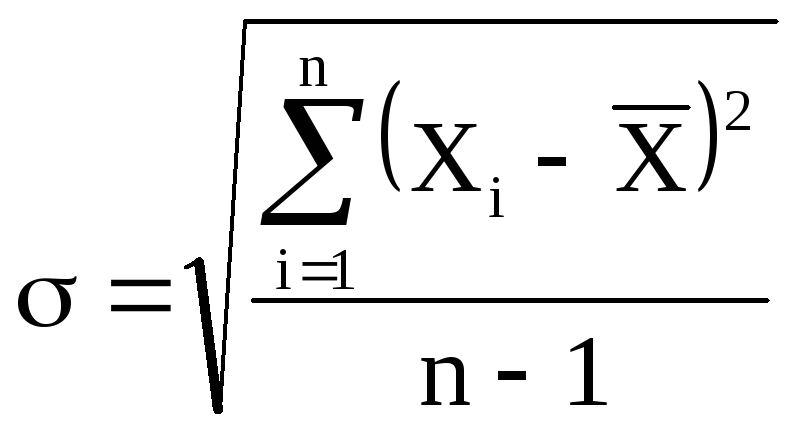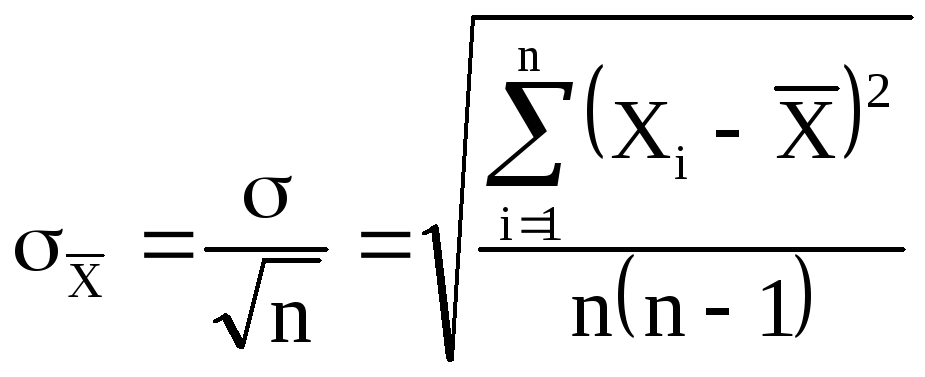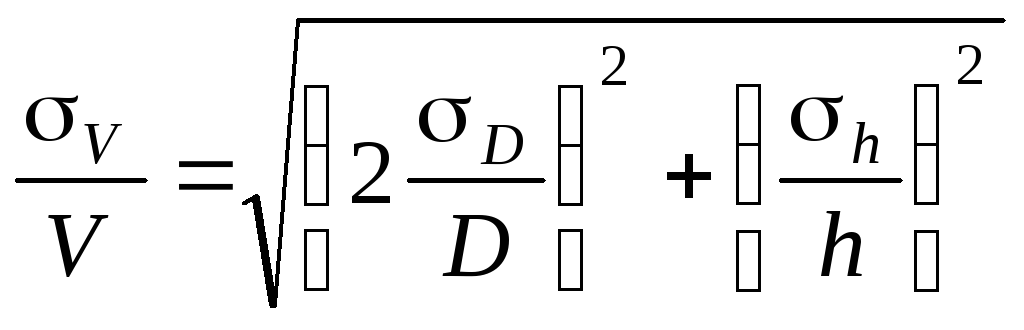Перевод
Ссылка на автора
Каждая модель машинного обучения пытается решить проблему с другой целью, используя свой набор данных, и, следовательно, важно понять контекст, прежде чем выбрать метрику. Обычно ответы на следующий вопрос помогают нам выбрать подходящий показатель:
- Тип задачи: регрессия? Классификация?
- Бизнес цель?
- Каково распределение целевой переменной?
Ну, в этом посте я буду обсуждать полезность каждой метрики ошибки в зависимости от цели и проблемы, которую мы пытаемся решить. Часть 1 фокусируется только на показателях оценки регрессии.
Метрики регрессии
- Средняя квадратическая ошибка (MSE)
- Среднеквадратическая ошибка (RMSE)
- Средняя абсолютная ошибка (MAE)
- R в квадрате (R²)
- Скорректированный R квадрат (R²)
- Среднеквадратичная ошибка в процентах (MSPE)
- Средняя абсолютная ошибка в процентах (MAPE)
- Среднеквадратичная логарифмическая ошибка (RMSLE)
Средняя квадратическая ошибка (MSE)
Это, пожалуй, самый простой и распространенный показатель для оценки регрессии, но, вероятно, наименее полезный. Определяется уравнением
гдеyᵢфактический ожидаемый результат иŷᵢэто прогноз модели.
MSE в основном измеряет среднеквадратичную ошибку наших прогнозов. Для каждой точки вычисляется квадратная разница между прогнозами и целью, а затем усредняются эти значения.
Чем выше это значение, тем хуже модель. Он никогда не бывает отрицательным, поскольку мы возводим в квадрат отдельные ошибки прогнозирования, прежде чем их суммировать, но для идеальной модели это будет ноль.
Преимущество:Полезно, если у нас есть неожиданные значения, о которых мы должны заботиться. Очень высокое или низкое значение, на которое мы должны обратить внимание.
Недостаток:Если мы сделаем один очень плохой прогноз, возведение в квадрат сделает ошибку еще хуже, и это может исказить метрику в сторону переоценки плохости модели. Это особенно проблематичное поведение, если у нас есть зашумленные данные (то есть данные, которые по какой-либо причине не совсем надежны) — даже в «идеальной» модели может быть высокий MSE в этой ситуации, поэтому становится трудно судить, насколько хорошо модель выполняет. С другой стороны, если все ошибки малы или, скорее, меньше 1, то ощущается противоположный эффект: мы можем недооценивать недостатки модели.
Обратите внимание, чтоесли мы хотим иметь постоянный прогноз, лучшим будетсреднее значение целевых значений.Его можно найти, установив производную нашей полной ошибки по этой константе в ноль, и найти ее из этого уравнения.
Среднеквадратическая ошибка (RMSE)
RMSE — это просто квадратный корень из MSE. Квадратный корень введен, чтобы масштаб ошибок был таким же, как масштаб целей.
Теперь очень важно понять, в каком смысле RMSE похож на MSE, и в чем разница.
Во-первых, они похожи с точки зрения их минимизаторов, каждый минимизатор MSE также является минимизатором для RMSE и наоборот, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора предсказаний, A и B, и скажем, что MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. И это также работает в противоположном направлении. ,
Что это значит для нас?
Это означает, что, если целевым показателем является RMSE, мы все равно можем сравнивать наши модели, используя MSE, поскольку MSE упорядочит модели так же, как RMSE. Таким образом, мы можем оптимизировать MSE вместо RMSE.
На самом деле, с MSE работать немного проще, поэтому все используют MSE вместо RMSE. Также есть небольшая разница между этими двумя моделями на основе градиента.
Это означает, что путешествие по градиенту MSE эквивалентно путешествию по градиенту RMSE, но с другой скоростью потока, и скорость потока зависит от самой оценки MSE.
Таким образом, хотя RMSE и MSE действительно схожи с точки зрения оценки моделей, они не могут быть сразу взаимозаменяемыми для методов на основе градиента. Возможно, нам нужно будет настроить некоторые параметры, такие как скорость обучения.
Средняя абсолютная ошибка (MAE)
В MAE ошибка рассчитывается как среднее абсолютных разностей между целевыми значениями и прогнозами. MAE — это линейная оценка, которая означает, чтовсе индивидуальные различия взвешены одинаковов среднем. Например, разница между 10 и 0 будет вдвое больше разницы между 5 и 0. Однако то же самое не верно для RMSE. Математически он рассчитывается по следующей формуле:
Что важно в этой метрике, так это то, что онанаказывает огромные ошибки, которые не так плохо, как MSE.Таким образом, он не так чувствителен к выбросам, как среднеквадратическая ошибка.
MAE широко используется в финансах, где ошибка в 10 долларов обычно в два раза хуже, чем ошибка в 5 долларов. С другой стороны, метрика MSE считает, что ошибка в 10 долларов в четыре раза хуже, чем ошибка в 5 долларов. MAE легче обосновать, чем RMSE.
Еще одна важная вещь в MAE — это его градиенты относительно прогнозов. Gradiend — это пошаговая функция, которая принимает -1, когда Y_hat меньше цели, и +1, когда она больше.
Теперь градиент не определен, когда предсказание является совершенным, потому что, когда Y_hat равен Y, мы не можем оценить градиент. Это не определено.
Таким образом, формально, MAE не дифференцируемо, но на самом деле, как часто ваши прогнозы точно измеряют цель. Даже если они это сделают, мы можем написать простое условие IF и вернуть ноль, если это так, и через градиент в противном случае. Также известно, что вторая производная везде нулевая и не определена в нулевой точке.
Обратите внимание, чтоесли мы хотим иметь постоянный прогноз, лучшим будетсрединное значение целевых значений.Его можно найти, установив производную нашей полной ошибки по этой константе в ноль, и найти ее из этого уравнения.
R в квадрате (R²)
А что если я скажу вам, что MSE для моих моделей предсказаний составляет 32? Должен ли я улучшить свою модель или она достаточно хороша? Или что, если мой MSE был 0,4? На самом деле, трудно понять, хороша наша модель или нет, посмотрев на абсолютные значения MSE или RMSE. Мы, вероятно, захотим измерить, как Во многом наша модель лучше, чем постоянная базовая линия.
Коэффициент детерминации, или R² (иногда читаемый как R-два), является еще одним показателем, который мы можем использовать для оценки модели, и он тесно связан с MSE, но имеет преимущество в том, чтобезмасштабное— не имеет значения, являются ли выходные значения очень большими или очень маленькими,R² всегда будет между -∞ и 1.
Когда R² отрицательно, это означает, что модель хуже, чем предсказание среднего значения.
MSE модели рассчитывается, как указано выше, в то время как MSE базовой линии определяется как:
гдеYс чертой означает среднее из наблюдаемогоyᵢ.
Чтобы сделать это более ясным, этот базовый MSE можно рассматривать как MSE, чтопростейшиймодель получит. Простейшей возможной моделью было бывсегдапредсказать среднее по всем выборкам. Значение, близкое к 1, указывает на модель с ошибкой, близкой к нулю, а значение, близкое к нулю, указывает на модель, очень близкую к базовой линии.
В заключение, R² — это соотношение между тем, насколько хороша наша модель, и тем, насколько хороша модель наивного среднего.
Распространенное заблуждение:Многие статьи в Интернете утверждают, что диапазон R² лежит между 0 и 1, что на самом деле не соответствует действительности. Максимальное значение R² равно 1, но минимальное может быть минус бесконечность.
Например, рассмотрим действительно дрянную модель, предсказывающую крайне отрицательное значение для всех наблюдений, даже если y_actual положительно. В этом случае R² будет меньше 0. Это крайне маловероятный сценарий, но возможность все еще существует.
MAE против MSE
Я заявил, что MAE более устойчив (менее чувствителен к выбросам), чем MSE, но это не значит, что всегда лучше использовать MAE. Следующие вопросы помогут вам решить:
Взять домой сообщение
В этой статье мы обсудили несколько важных метрик регрессии. Сначала мы обсудили среднеквадратичную ошибку и поняли, что наилучшей константой для нее является среднее целевое значение. Среднеквадратичная ошибка и R² очень похожи на MSE с точки зрения оптимизации. Затем мы обсудили среднюю абсолютную ошибку и когда люди предпочитают использовать MAE вместо MSE.
Спасибо за чтение, и я с нетерпением жду, чтобы услышать ваши вопросы 
P.SСледите за моей следующей статьей, которая изучает другие более продвинутые метрики регрессии. Если вы хотите больше узнать о мире машинного обучения, вы также можете подписаться на меня в Instagram, напишите мне напрямую или найди меня на linkedin, Я хотел бы услышать от вас.
Ресурсы:
[1] https://dmitryulyanov.github.io/about
In the previous post, we saw the various metrics which are used to assess a machine learning model’s performance. Among those, the confusion matrix is used to evaluate a classification problem’s accuracy. On the other hand, mean squared error (MSE), and mean absolute error (MAE) are used to evaluate the regression problem’s accuracy.
The F1 score is useful when the size of the positive class is relatively small.
ROC Area Under Curve is useful when we are not concerned about whether the small dataset/class of dataset is positive or not, in contrast to the F1 score where the class being positive is important.

In today’s post, we will understand what MAE is and explore more about what it means to vary these metrics. In addition to this, we will discuss a few more metrics that will help us decide if the machine learning model would be useful in real-life scenarios or not.
1. What is Mean Absolute Error or MAE
Mean Absolute Error(MAE) is the mean size of the mistakes in collected predictions. We know that an error basically is the absolute difference between the actual or true values and the values that are predicted. The absolute difference means that if the result has a negative sign, it is ignored.
Hence, MAE = True values – Predicted values
MAE takes the average of this error from every sample in a dataset and gives the output.
This can be implemented using sklearn’s mean_absolute_error method:
from sklearn.metrics import mean_absolute_error
# predicting home prices in some area
predicted_home_prices = mycity_model.predict(X)
mean_absolute_error(y, predicted_home_prices)But this value might not be the relevant aspect that can be considered while dealing with a real-life situation because the data we use to build the model as well as evaluate it is the same, which means the model has no exposure to real, never-seen-before data. So, it may perform extremely well on seen data but might fail miserably when it encounters real, unseen data.
The concepts of underfitting and overfitting can be pondered over, from here:
Underfitting: The scenario when a machine learning model almost exactly matches the training data but performs very poorly when it encounters new data or validation set.
Overfitting: The scenario when a machine learning model is unable to capture the important patterns and insights from the data, which results in the model performing poorly on training data itself.
P.S. In the upcoming posts, we will understand how to fit the model in the right way using many methods like feature normalization, feature generation, and much more.
2. What is Mean Squared Error or MSE
The Mean Absolute Error is the squared mean of the difference between the actual values and predictable values.
How do you Calculate MSE?
Steps to calculate the MSE from a set of X and Y values:
- First, Find the regression line.
- Insert the X values into the linear regression equation to find the new Y values (Y’).
- Subtract the new Y value from the original to get the error.
- Square the values that you go as errors.
- Add up the errors
- Find the mean.
Hence, MSE =
Here N is the total number of observations/rows in the dataset. The sigma symbol denotes the difference between actual and predicted values taken on every i value ranging from 1 to n.
This can be implemented using sklearn‘s mean_squared_error method:
from sklearn.metrics import mean_squared_error
actual_values = [3, -0.5, 2, 7]
predicted_values = [2.5, 0.0, 2, 8]
mean_squared_error(actual_values, predicted_values)In most regression problems, mean squared error is used to determine the model’s performance.
3. What is Root Mean Squared Error or RMSE
RMSE is the standard deviation of the errors which occur when a prediction is made on a dataset. This is the same as MSE (Mean Squared Error) but the root of the value is considered while determining the accuracy of the model.
from sklearn.metrics import mean_squared_error
from math import sqrt
actual_values = [3, -0.5, 2, 7]
predicted_values = [2.5, 0.0, 2, 8]
mean_squared_error(actual_values, predicted_values)
# taking root of mean squared error
root_mean_squared_error = sqrt(mean_squared_error)4. R Squared
It is also known as the coefficient of determination. This metric gives an indication of how good a model fits a given dataset. It indicates how close the regression line (i.e the predicted values plotted) is to the actual data values. The R squared value lies between 0 and 1 where 0 indicates that this model doesn’t fit the given data and 1 indicates that the model fits perfectly to the dataset provided.
import numpy as np
X = np.random.randn(100)
y = np.random.randn(60) # y has nothing to do with X whatsoever
from sklearn.linear_model import LinearRegression
from sklearn.cross_validation import cross_val_score
scores = cross_val_score(LinearRegression(), X, y,scoring='r2')Where to use which Metric to determine the Performance of a Machine Learning Model?
MAE: It is not very sensitive to outliers in comparison to MSE since it doesn’t punish huge errors. It is usually used when the performance is measured on continuous variable data. It gives a linear value, which averages the weighted individual differences equally. The lower the value, the better the model’s performance.
MSE: It is one of the most commonly used metrics, but least useful when a single bad prediction would ruin the entire model’s predicting abilities, i.e when the dataset contains a lot of noise. It is most useful when the dataset contains outliers, or unexpected values (too high or too low values).
RMSE: In RMSE, the errors are squared before they are averaged. This basically implies that RMSE assigns a higher weight to larger errors. This indicates that RMSE is much more useful when large errors are present and they drastically affect the model’s performance. It avoids taking the absolute value of the error and this trait is useful in many mathematical calculations. In this metric also, the lower the value, the better the performance of the model.
Conclusion
Mean Squared Error (MSE), Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and R-Squared (R2) are all popular metrics for assessing the precision of machine learning algorithms. MSE and MAE report the average difference between predicted and real values, whereas RMSE reports the same information but in the same unit as the objective variable. R2 is the percentage of variance in the objective variable described by the model. These metrics are useful for evaluating model success and comparing various models.
Frequently Asked Questions(FAQs)
1. What is the purpose of Mean Squared Error (MSE) in machine learning?
MSE measures the average difference between predicted and actual values.
2. How do you calculate Root Mean Squared Error (RMSE)?
RMSE is the square root of the average squared difference between predicted and actual values.
3. What is the significance of R-Squared (R²) in machine learning?
R² measures the proportion of variance in the target variable that is explained by the model.
4. How can Mean Absolute Error (MAE) help to evaluate model performance?
MAE measures the average absolute difference between predicted and actual values, providing a more easily interpretable metric for non-normal distributions.
5. How do you calculate MSE?
- First, Find the regression line.
- Insert the X values into the linear regression equation to find the new Y values (Y’).
- Subtract the new Y value from the original to get the error.
- Square the values that you go as errors.
- Add up the errors
- Find the mean.
You may also like:
- How Good is my Machine Learning Model? How do I improve its Performance?
- Machine Learning — How to deal with missing data using Python?
- Machine Learning and Data Visualization using Orange
- Designing a Learning System | The first step to Machine Learning
17 авг. 2022 г.
читать 3 мин
Модели регрессии используются для количественной оценки взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика .
Всякий раз, когда мы подбираем регрессионную модель, мы хотим понять, насколько хорошо модель может использовать значения переменных-предикторов для прогнозирования значения переменной отклика.
Две метрики, которые мы часто используем для количественной оценки того, насколько хорошо модель соответствует набору данных, — это средняя абсолютная ошибка (MAE) и среднеквадратическая ошибка (RMSE), которые рассчитываются следующим образом:
MAE : метрика, которая сообщает нам среднюю абсолютную разницу между прогнозируемыми значениями и фактическими значениями в наборе данных. Чем ниже MAE, тем лучше модель соответствует набору данных.
MAE = 1/n * Σ|y i – ŷ i |
куда:
- Σ — это символ, который означает «сумма»
- y i — наблюдаемое значение для i -го наблюдения
- ŷ i — прогнозируемое значение для i -го наблюдения
- n — размер выборки
RMSE : метрика, которая сообщает нам квадратный корень из средней квадратичной разницы между прогнозируемыми значениями и фактическими значениями в наборе данных. Чем ниже RMSE, тем лучше модель соответствует набору данных.
Он рассчитывается как:
СКО = √ Σ(y i – ŷ i ) 2 / n
куда:
- Σ — это символ, который означает «сумма»
- ŷ i — прогнозируемое значение для i -го наблюдения
- y i — наблюдаемое значение для i -го наблюдения
- n — размер выборки
Пример: Расчет RMSE и MAE
Предположим, мы используем регрессионную модель, чтобы предсказать количество очков, которое 10 игроков наберут в баскетбольном матче.
В следующей таблице показаны прогнозируемые очки по модели и фактические очки, набранные игроками:
Используя калькулятор MAE , мы можем рассчитать MAE как 3,2.
Это говорит нам о том, что средняя абсолютная разница между прогнозируемыми значениями модели и фактическими значениями составляет 3,2.
Используя Калькулятор RMSE , мы можем рассчитать RMSE, чтобы он был равен 4 .
Это говорит нам о том, что квадратный корень из среднеквадратичной разницы между предсказанными набранными очками и фактическими набранными очками равен 4.
Обратите внимание, что каждая метрика дает нам представление о типичной разнице между прогнозируемым значением, сделанным моделью, и фактическим значением в наборе данных, но интерпретация каждой метрики немного отличается.
RMSE против MAE: какую метрику следует использовать?
Если вы хотите придать больший вес наблюдениям, которые находятся дальше от среднего (т. е. если «отклонение» на 20 более чем в два раза хуже, чем отклонение на 10 дюймов), то лучше использовать RMSE для измерения ошибки, потому что RMSE более чувствителен к наблюдениям, которые далеки от среднего.
Однако, если «выключиться» в 20 раз хуже, чем в 10, то лучше использовать MAE.
Чтобы проиллюстрировать это, предположим, что у нас есть один игрок, который явно отличается по количеству набранных очков:
Используя онлайн-калькуляторы, упомянутые ранее, мы можем рассчитать MAE и RMSE следующим образом:
- МАЭ : 8
- Среднеквадратичное значение : 16,4356
Обратите внимание, что RMSE увеличивается намного больше, чем MAE.
Это связано с тем, что в формуле RMSE используются квадраты разницы, а квадрат разницы между наблюдаемым значением 76 и прогнозируемым значением 22 довольно велик. Это приводит к значительному увеличению значения RMSE.
На практике мы обычно подгоняем несколько моделей регрессии к набору данных и вычисляем только одну из этих метрик для каждой модели.
Например, мы можем подобрать три разные регрессионные модели и рассчитать RMSE для каждой модели. Затем мы выберем модель с самым низким значением RMSE в качестве «лучшей» модели, потому что именно она делает прогнозы, наиболее близкие к фактическим значениям из набора данных.
В любом случае просто убедитесь, что вы вычисляете одну и ту же метрику для каждой модели. Например, не рассчитывайте MAE для одной модели и RMSE для другой модели, а затем сравнивайте эти две метрики.
Дополнительные ресурсы
В следующих руководствах объясняется, как рассчитать MAE с помощью различных статистических программ:
Как рассчитать среднюю абсолютную ошибку в Excel
Как рассчитать среднюю абсолютную ошибку в R
Как рассчитать среднюю абсолютную ошибку в Python
В следующих руководствах объясняется, как рассчитать RMSE с помощью различных статистических программ:
Как рассчитать среднеквадратичную ошибку в Excel
Как рассчитать среднеквадратичную ошибку в R
Как рассчитать среднеквадратичную ошибку в Python
Полиномиальная регрессия и метрики качества модели
Время на прочтение
4 мин
Количество просмотров 11K

Давайте разберемся на примере. Скажем, я хочу спрогнозировать зарплату специалиста по данным на основе количества лет опыта. Итак, моя целевая переменная (Y) — это зарплата, а независимая переменная (X) — опыт. У меня есть случайные данные по X и Y, и мы будем использовать линейную регрессию для прогнозирования заработной платы. Давайте использовать pandas и scikit-learn для загрузки данных и создания линейной модели.
import pandas as pd
from sklearn.linear_model import LinearRegression
sal_data={"Exp":[2,2.2, 2.8, 4, 7, 8, 11, 12, 21, 25],
"Salary": [7, 8, 11, 15, 22, 29, 37 ,45.7, 49, 52]}
#Load data into a pandas Dataframe
df=pd.DataFrame(sal_data)
df.head(3)from bokeh.plotting import figure, show, output_file
p=figure(title="Actual vs Predicted Salary", width=450, height=300)
p.title.align = 'center'
p.circle(df.Exp, df.Salary)
p.line(df.Exp, df.Salary, legend_label='Actual Salary', line_width=3, line_alpha=0.4)
p.circle(df.Exp, yp, color="red")
p.line(df.Exp,yp, color="red",legend_label='Predicted Salary', line_width=3, line_alpha=0.4)
p.xaxis.axis_label = 'Experience'
p.yaxis.axis_label = 'Salary'
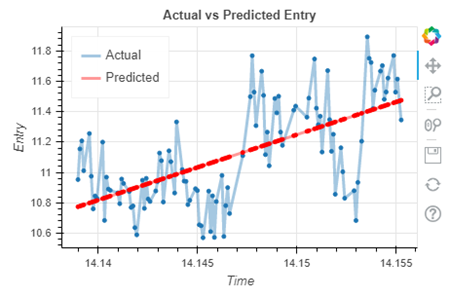
show(p)Из приведенного выше графика мы видим, что существует разрыв между прогнозируемыми и фактическими точками данных. Получается, что линейная функция не может достаточно хорошо описать наши данные. Исходя из жизненного опыта, мы так же можем предположить, что увеличение зарплаты сотрудника происходит не линейно, а в зависимости от опыта работы: чем больше опыт – тем больше повышение!
Статистически разрыв / разница между графиками называется остатками и обычно является ошибкой в RMSE и MAE.
Среднеквадратичная ошибка (RMSE) и средняя абсолютная ошибка (MAE) — это метрики, используемые для оценки работы модели регрессии. Эти показатели говорят нам, насколько точны наши прогнозы и какова величина отклонения от фактических значений.
Технически, RMSE — это корень среднего квадрата ошибок, а MAE — это среднее абсолютное значение ошибок. Здесь ошибки — это различия между предсказанными значениями (значениями, предсказанными нашей регрессионной моделью) и фактическими значениями переменной. По своей сути разница лишь в том, что RMSE из-за квадрата в формуле будет сильнее наказывать нас за ошибку, т.е. будет увеличивать вес / значение самой ошибки. Метрики рассчитываются следующим образом:
Yi – настоящее значение
Yp – предсказанное значение
n – кол-во наблюдений
Scikit-learn предоставляет библиотеку показателей для расчета этих значений. Однако мы будем вычислять RMSE и MAE, используя приведенные выше математические выражения. Оба метода дадут одинаковый результат.
import numpy as np
print(f'Residuals: {y-yp}')
np.sqrt(np.mean(np.square(y-yp))) #RMSE
np.mean(abs(y-yp)) #MAE
#RMSE/MAE computation using sklearn library
from sklearn.metrics import mean_squared_error, mean_absolute_errornp.sqrt(mean_squared_error(y, yp))
mean_absolute_error(y, yp)6.48
5.68Давайте попробуем составить полиномиальное преобразование (X) и совершить предсказание с той же моделью, чтобы посмотреть, уменьшатся ли наши ошибки. Для этого используем Scikit-learn PolynomialFeatures
from sklearn.preprocessing import PolynomialFeatures
pf=PolynomialFeatures()
#Linear Equation of degree 2
X_poly=pf.fit_transform(X)
lm.fit(X_poly, y)
yp=lm.predict(X_poly)То же действие можно сделать вручную и для любой степени полинома:
def generate_degrees(source_data: list, degree: int):
return np.array([source_data**n for n in range(1, degree + 1)]).TВычисляем метрики:
#RMSE and MAE
np.sqrt(np.mean(np.square(y-yp)))
np.mean(abs(y-yp))2.3974
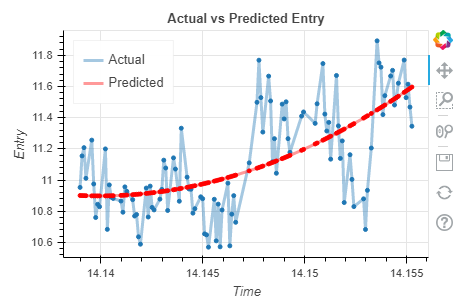
1.6386На этот раз они намного ниже. Давайте построим графики y и yp (как мы делали раньше), чтобы проверить совпадение:
Разрыв между двумя строками уменьшился, а метрики качества модели стали лучше!
Давайте разберем подобную задачу не на искусственных, а на реальных данных. Посмотрим на уже предобработанные данные по входам в систему онлайн трейдинга.
В переменной y_train хранится количество людей, зашедших во время x_train. Вполне обычная задача, решаемая линейной регрессией:
Модель отработала с ошибками MAE и RMSE в 0.602 и 0.616 соответственно. Такое высокое число ошибок связанно с тем, что данные имеют сильный разброс относительно линии регрессии. Однако, мы можем предположить, что для такого примера так же недостаточно лишь функции линейной регрессии. Давайте проверим эту гипотезу и попробуем применить полиномиальную регрессию и посмотреть метрики качества модели для полинома 2 степени:
Данная же модель отработала с ошибками MAE и RMSE в 0.498 и 0.543 соответственно, и визуально мы можем интерпретировать, что наша модель лучше стала описывать данные.
Почему же не использовать функцию большего количества степеней, 3, 15, 100? Ведь тогда метрики качества модели будут лишь улучшаться! Но не все так просто. Конечно, модель лучше станет описывать наши данные, а при совсем большом количестве степеней график станет аналогичен изначальному графику, но обобщающая способность модели сильно снизится, и она будет работать хорошо только лишь в данном наборе данных и не сможет должным образом сделать predict новых значений.
Таким образом мы разобрались в основных метриках качества работы модели и на их примере показали, что использование полиномиальной регрессии зачастую дает лучшие результаты, чем линейная. Однако всегда нужно отталкиваться от поставленной задачи.
Хочу отметить, что повысить метрики качества модели MAE и RMSE можно и другими способами. Некоторые из методов, которые мы можем использовать, включают в себя:
-
Функции преобразования / масштабирования
-
Обработка выбросов (если их много)
-
Добавление новых фичей
-
Использование разных алгоритмов
-
Настройка гиперпараметров модели
Для того чтобы модель линейной регрессии можно было применять на практике необходимо сначала оценить её качество. Для этих целей предложен ряд показателей, каждый из которых предназначен для использования в различных ситуациях и имеет свои особенности применения (линейные и нелинейные, устойчивые к аномалиям, абсолютные и относительные, и т.д.). Корректный выбор меры для оценки качества модели является одним из важных факторов успеха в решении задач анализа данных.
«Хорошая» аналитическая модель должна удовлетворять двум, зачастую противоречивым, требованиям — как можно лучше соответствовать данным и при этом быть удобной для интерпретации пользователем. Действительно, повышение соответствия модели данным как правило связано с её усложнением (в случае регрессии — увеличением числа входных переменных модели). А чем сложнее модель, тем ниже её интерпретируемость.
Поэтому при выборе между простой и сложной моделью последняя должна значимо увеличивать соответствие модели данным чтобы оправдать рост сложности и соответствующее снижение интерпретируемости. Если это условие не выполняется, то следует выбрать более простую модель.
Таким образом, чтобы оценить, насколько повышение сложности модели значимо увеличивает её точность, необходимо использовать аппарат оценки качества регрессионных моделей. Он включает в себя следующие меры:
- Среднеквадратичная ошибка (MSE).
- Корень из среднеквадратичной ошибки (RMSE).
- Среднеквадратичная ошибка в процентах (MSPE).
- Средняя абсолютная ошибка (MAE).
- Средняя абсолютная ошибка в процентах (MAPE).
- Cимметричная средняя абсолютная процентная ошибка (SMAPE).
- Средняя абсолютная масштабированная ошибка (MASE)
- Средняя относительная ошибка (MRE).
- Среднеквадратичная логарифмическая ошибка (RMSLE).
- Коэффициент детерминации R-квадрат.
- Скорректированный коэффициент детеминации.
Прежде чем перейти к изучению метрик качества, введём некоторые базовые понятия, которые нам в этом помогут. Для этого рассмотрим рисунок.
Рисунок 1. Линейная регрессия
Наклонная прямая представляет собой линию регрессии с переменной, на которой расположены точки, соответствующие предсказанным значениям выходной переменной widehat{y} (кружки синего цвета). Оранжевые кружки представляют фактические (наблюдаемые) значения y . Расстояния между ними и линией регрессии — это ошибка предсказания модели y-widehat{y} (невязка, остатки). Именно с её использованием вычисляются все приведённые в статье меры качества.
Горизонтальная линия представляет собой модель простого среднего, где коэффициент при независимой переменной x равен нулю, и остаётся только свободный член b, который становится равным среднему арифметическому фактических значений выходной переменной, т.е. b=overline{y}. Очевидно, что такая модель для любого значения входной переменной будет выдавать одно и то же значение выходной — overline{y}.
В линейной регрессии такая модель рассматривается как «бесполезная», хуже которой работает только «случайный угадыватель». Однако, она используется для оценки, насколько дисперсия фактических значений y относительно линии среднего, больше, чем относительно линии регрессии с переменной, т.е. насколько модель с переменной лучше «бесполезной».
MSE
Среднеквадратичная ошибка (Mean Squared Error) применяется в случаях, когда требуется подчеркнуть большие ошибки и выбрать модель, которая дает меньше именно больших ошибок. Большие значения ошибок становятся заметнее за счет квадратичной зависимости.
Действительно, допустим модель допустила на двух примерах ошибки 5 и 10. В абсолютном выражении они отличаются в два раза, но если их возвести в квадрат, получив 25 и 100 соответственно, то отличие будет уже в четыре раза. Таким образом модель, которая обеспечивает меньшее значение MSE допускает меньше именно больших ошибок.
MSE рассчитывается по формуле:
MSE=frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y}_{i})^{2},
где n — количество наблюдений по которым строится модель и количество прогнозов, y_{i} — фактические значение зависимой переменной для i-го наблюдения, widehat{y}_{i} — значение зависимой переменной, предсказанное моделью.
Таким образом, можно сделать вывод, что MSE настроена на отражение влияния именно больших ошибок на качество модели.
Недостатком использования MSE является то, что если на одном или нескольких неудачных примерах, возможно, содержащих аномальные значения будет допущена значительная ошибка, то возведение в квадрат приведёт к ложному выводу, что вся модель работает плохо. С другой стороны, если модель даст небольшие ошибки на большом числе примеров, то может возникнуть обратный эффект — недооценка слабости модели.
RMSE
Корень из среднеквадратичной ошибки (Root Mean Squared Error) вычисляется просто как квадратный корень из MSE:
RMSE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y_{i}})^{2}}
MSE и RMSE могут минимизироваться с помощью одного и того же функционала, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора результатов работы модели, A и B, и MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. Справедливо и обратное: если MSE(A)<MSE(B), то и RMSE(A)<RMSE(B).
Следовательно, сравнение моделей с помощью RMSE даст такой же результат, что и для MSE. Однако с MSE работать несколько проще, поэтому она более популярна у аналитиков. Кроме этого, имеется небольшая разница между этими двумя ошибками при оптимизации с использованием градиента:
frac{partial RMSE}{partial widehat{y}_{i}}=frac{1}{2sqrt{MSE}}frac{partial MSE}{partial widehat{y}_{i}}
Это означает, что перемещение по градиенту MSE эквивалентно перемещению по градиенту RMSE, но с другой скоростью, и скорость зависит от самой оценки MSE. Таким образом, хотя RMSE и MSE близки с точки зрения оценки моделей, они не являются взаимозаменяемыми при использовании градиента для оптимизации.
Влияние каждой ошибки на RMSE пропорционально величине квадрата ошибки. Поэтому большие ошибки оказывают непропорционально большое влияние на RMSE. Следовательно, RMSE можно считать чувствительной к аномальным значениям.
MSPE
Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error) представляет собой относительную ошибку, где разность между наблюдаемым и фактическим значениями делится на наблюдаемое значение и выражается в процентах:
MSPE=frac{100}{n}sumlimits_{i=1}^{n}left ( frac{y_{i}-widehat{y}_{i}}{y_{i}} right )^{2}
Проблемой при использовании MSPE является то, что, если наблюдаемое значение выходной переменной равно 0, значение ошибки становится неопределённым.
MSPE можно рассматривать как взвешенную версию MSE, где вес обратно пропорционален квадрату наблюдаемого значения. Таким образом, при возрастании наблюдаемых значений ошибка имеет тенденцию уменьшаться.
MAE
Cредняя абсолютная ошибка (Mean Absolute Error) вычисляется следующим образом:
MAE=frac{1}{n}sumlimits_{i=1}^{n}left | y_{i}-widehat{y}_{i} right |
Т.е. MAE рассчитывается как среднее абсолютных разностей между наблюдаемым и предсказанным значениями. В отличие от MSE и RMSE она является линейной оценкой, а это значит, что все ошибки в среднем взвешены одинаково. Например, разница между 0 и 10 будет вдвое больше разницы между 0 и 5. Для MSE и RMSE, как отмечено выше, это не так.
Поэтому MAE широко используется, например, в финансовой сфере, где ошибка в 10 долларов должна интерпретироваться как в два раза худшая, чем ошибка в 5 долларов.
MAPE
Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error) вычисляется следующим образом:
MAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{left | y_{i} right |}
Эта ошибка не имеет размерности и очень проста в интерпретации. Её можно выражать как в долях, так и в процентах. Если получилось, например, что MAPE=11.4, то это говорит о том, что ошибка составила 11.4% от фактического значения.
SMAPE
Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error) — это мера точности, основанная на процентных (или относительных) ошибках. Обычно определяется следующим образом:
SMAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{(left | y_{i} right |+left | widehat{y}_{i} right |)/2}
Т.е. абсолютная разность между наблюдаемым и предсказанным значениями делится на полусумму их модулей. В отличие от обычной MAPE, симметричная имеет ограничение на диапазон значений. В приведённой формуле он составляет от 0 до 200%. Однако, поскольку диапазон от 0 до 100% гораздо удобнее интерпретировать, часто используют формулу, где отсутствует деление знаменателя на 2.
Одной из возможных проблем SMAPE является неполная симметрия, поскольку в разных диапазонах ошибка вычисляется неодинаково. Это иллюстрируется следующим примером: если y_{i}=100 и widehat{y}_{i}=110, то SMAPE=4.76, а если y_{i}=100 и widehat{y}_{i}=90, то SMAPE=5.26.
Ограничение SMAPE заключается в том, что, если наблюдаемое или предсказанное значение равно 0, ошибка резко возрастет до верхнего предела (200% или 100%).
MASE
Средняя абсолютная масштабированная ошибка (Mean absolute scaled error) — это показатель, который позволяет сравнивать две модели. Если поместить MAE для новой модели в числитель, а MAE для исходной модели в знаменатель, то полученное отношение и будет равно MASE. Если значение MASE меньше 1, то новая модель работает лучше, если MASE равно 1, то модели работают одинаково, а если значение MASE больше 1, то исходная модель работает лучше, чем новая модель. Формула для расчета MASE имеет вид:
MASE=frac{MAE_{i}}{MAE_{j}}
MASE симметрична и устойчива к выбросам.
MRE
Средняя относительная ошибка (Mean Relative Error) вычисляется по формуле:
MRE=frac{1}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y}_{i}right |}{left | y_{i} right |}
Несложно увидеть, что данная мера показывает величину абсолютной ошибки относительно фактического значения выходной переменной (поэтому иногда эту ошибку называют также средней относительной абсолютной ошибкой, MRAE). Действительно, если значение абсолютной ошибки, скажем, равно 10, то сложно сказать много это или мало. Например, относительно значения выходной переменной, равного 20, это составляет 50%, что достаточно много. Однако относительно значения выходной переменной, равного 100, это будет уже 10%, что является вполне нормальным результатом.
Очевидно, что при вычислении MRE нельзя применять наблюдения, в которых y_{i}=0.
Таким образом, MRE позволяет более адекватно оценить величину ошибки, чем абсолютные ошибки. Кроме этого она является безразмерной величиной, что упрощает интерпретацию.
RMSLE
Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error) представляет собой RMSE, вычисленную в логарифмическом масштабе:
RMSLE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(log(widehat{y}_{i}+1)-log{(y_{i}+1}))^{2}}
Константы, равные 1, добавляемые в скобках, необходимы чтобы не допустить обращения в 0 выражения под логарифмом, поскольку логарифм нуля не существует.
Известно, что логарифмирование приводит к сжатию исходного диапазона изменения значений переменной. Поэтому применение RMSLE целесообразно, если предсказанное и фактическое значения выходной переменной различаются на порядок и больше.
R-квадрат
Перечисленные выше ошибки не так просто интерпретировать. Действительно, просто зная значение средней абсолютной ошибки, скажем, равное 10, мы сразу не можем сказать хорошая это ошибка или плохая, и что нужно сделать чтобы улучшить модель.
В этой связи представляет интерес использование для оценки качества регрессионной модели не значения ошибок, а величину показывающую, насколько данная модель работает лучше, чем модель, в которой присутствует только константа, а входные переменные отсутствуют или коэффициенты регрессии при них равны нулю.
Именно такой мерой и является коэффициент детерминации (Coefficient of determination), который показывает долю дисперсии зависимой переменной, объяснённой с помощью регрессионной модели. Наиболее общей формулой для вычисления коэффициента детерминации является следующая:
R^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}}
Практически, в числителе данного выражения стоит среднеквадратическая ошибка оцениваемой модели, а в знаменателе — модели, в которой присутствует только константа.
Главным преимуществом коэффициента детерминации перед мерами, основанными на ошибках, является его инвариантность к масштабу данных. Кроме того, он всегда изменяется в диапазоне от −∞ до 1. При этом значения близкие к 1 указывают на высокую степень соответствия модели данным. Очевидно, что это имеет место, когда отношение в формуле стремится к 0, т.е. ошибка модели с переменными намного меньше ошибки модели с константой. R^{2}=0 показывает, что между независимой и зависимой переменными модели имеет место функциональная зависимость.
Когда значение коэффициента близко к 0 (т.е. ошибка модели с переменными примерно равна ошибке модели только с константой), это указывает на низкое соответствие модели данным, когда модель с переменными работает не лучше модели с константой.
Кроме этого, бывают ситуации, когда коэффициент R^{2} принимает отрицательные значения (обычно небольшие). Это произойдёт, если ошибка модели среднего становится меньше ошибки модели с переменной. В этом случае оказывается, что добавление в модель с константой некоторой переменной только ухудшает её (т.е. регрессионная модель с переменной работает хуже, чем предсказание с помощью простой средней).
На практике используют следующую шкалу оценок. Модель, для которой R^{2}>0.5, является удовлетворительной. Если R^{2}>0.8, то модель рассматривается как очень хорошая. Значения, меньшие 0.5 говорят о том, что модель плохая.
Скорректированный R-квадрат
Основной проблемой при использовании коэффициента детерминации является то, что он увеличивается (или, по крайней мере, не уменьшается) при добавлении в модель новых переменных, даже если эти переменные никак не связаны с зависимой переменной.
В связи с этим возникают две проблемы. Первая заключается в том, что не все переменные, добавляемые в модель, могут значимо увеличивать её точность, но при этом всегда увеличивают её сложность. Вторая проблема — с помощью коэффициента детерминации нельзя сравнивать модели с разным числом переменных. Чтобы преодолеть эти проблемы используют альтернативные показатели, одним из которых является скорректированный коэффициент детерминации (Adjasted coefficient of determinftion).
Скорректированный коэффициент детерминации даёт возможность сравнивать модели с разным числом переменных так, чтобы их число не влияло на статистику R^{2}, и накладывает штраф за дополнительно включённые в модель переменные. Вычисляется по формуле:
R_{adj}^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}/(n-k)}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}/(n-1)}
где n — число наблюдений, на основе которых строится модель, k — количество переменных в модели.
Скорректированный коэффициент детерминации всегда меньше единицы, но теоретически может принимать значения и меньше нуля только при очень малом значении обычного коэффициента детерминации и большом количестве переменных модели.
Сравнение метрик
Резюмируем преимущества и недостатки каждой приведённой метрики в следующей таблице:
| Мера | Сильные стороны | Слабые стороны |
|---|---|---|
| MSE | Позволяет подчеркнуть большие отклонения, простота вычисления. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. Сложность интерпретации из-за квадратичной зависимости. |
| RMSE | Простота интерпретации, поскольку измеряется в тех же единицах, что и целевая переменная. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. |
| MSPE | Нечувствительна к выбросам. Хорошо интерпретируема, поскольку имеет линейный характер. | Поскольку вклад всех ошибок отдельных наблюдений взвешивается одинаково, не позволяет подчёркивать большие и малые ошибки. |
| MAPE | Является безразмерной величиной, поэтому её интерпретация не зависит от предметной области. | Нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю. |
| SMAPE | Позволяет корректно работать с предсказанными значениями независимо от того больше они фактического, или меньше. | Приближение к нулю фактического или предсказанного значения приводит к резкому росту ошибки, поскольку в знаменателе присутствует как фактическое, так и предсказанное значения. |
| MASE | Не зависит от масштаба данных, является симметричной: положительные и отрицательные отклонения от фактического значения учитываются одинаково. Устойчива к выбросам. Позволяет сравнивать модели. | Сложность интерпретации. |
| MRE | Позволяет оценить величину ошибки относительно значения целевой переменной. | Неприменима для наблюдений с нулевым значением выходной переменной. |
| RMSLE | Логарифмирование позволяет сделать величину ошибки более устойчивой, когда разность между фактическим и предсказанным значениями различается на порядок и выше | Может быть затруднена интерпретация из-за нелинейности. |
| R-квадрат | Универсальность, простота интерпретации. | Возрастает даже при включении в модель бесполезных переменных. Плохо работает когда входные переменные зависимы. |
| R-квадрат скорр. | Корректно отражает вклад каждой переменной в модель. | Плохо работает, когда входные переменные зависимы. |
В данной статье рассмотрены наиболее популярные меры качества регрессионных моделей, которые часто используются в различных аналитических приложениях. Эти меры имеют свои особенности применения, знание которых позволит обоснованно выбирать и корректно применять их на практике.
Однако в литературе можно встретить и другие меры качества моделей регрессии, которые предлагаются различными авторами для решения конкретных задач анализа данных.
Другие материалы по теме:
Отбор переменных в моделях линейной регрессии
Репрезентативность выборочных данных
Логистическая регрессия и ROC-анализ — математический аппарат
RMSE
- Среднеквадратичная ошибка, среднеквадратичная ошибка
- Это квадратный корень из отношения суммы квадратов отклонения между значением наблюдения и истинным значением к количеству m наблюдений.
- Он используется для измерения отклонения между наблюдаемым значением и истинным значением.
MAE
- Средняя абсолютная ошибка, средняя абсолютная ошибка
- Среднее значение абсолютных ошибок
- Он может лучше отражать реальную ситуацию с ошибкой предсказанного значения.
Стандартное отклонение
- Стандартное отклонение, стандартное отклонение
- Квадратный корень из дисперсии
- Используется для измерения степени разброса набора чисел
Сравнение RMSE и стандартного отклонения:
Стандартное отклонение используется для измерения степени разброса набора чисел, а среднеквадратичная ошибка используется для измерения отклонения между наблюдаемым значением и истинным значением. Их объекты исследования и исследовательские цели различны, но процесс расчета аналогичен.
Сравнение RMSE и MAE:
RMSE эквивалентно норме L2, а MAE эквивалентно норме L1. Чем больше число раз, тем больше результат вычисления связан с большим значением, в то время как меньшее значение игнорируется, поэтому RMSE более чувствителен к выбросам (то есть, если есть прогнозируемое значение, которое сильно отличается от истинного значения, то RMSE Будет огромно).
Средняя квадратичная ошибка.
При ответственных
измерениях, когда необходимо знать
надежность полученных результатов,
используется средняя квадратичная
ошибка (или
стандартное отклонение), которая
определяется формулой
(5)
Величина
характеризует отклонение отдельного
единичного измерения от истинного
значения.
Если мы вычислили
по n
измерениям среднее значение
по формуле (2), то это значение будет
более точным, то есть будет меньше
отличаться от истинного, чем каждое
отдельное измерение. Средняя квадратичная
ошибка среднего значения
равна
(6)
где — среднеквадратичная
ошибка каждого отдельного измерения,
n
– число
измерений.
Таким образом,
увеличивая число опытов, можно уменьшить
случайную ошибку в величине среднего
значения.
В настоящее время
результаты научных и технических
измерений принято представлять в виде
(7)
Как показывает
теория, при такой записи мы знаем
надежность полученного результата, а
именно, что истинная величина Х с
вероятностью 68% отличается от
не более, чем на
.
При использовании
же средней арифметической (абсолютной)
ошибки (формула 2) о надежности результата
ничего сказать нельзя. Некоторое
представление о точности проведенных
измерений в этом случае дает относительная
ошибка (формула 4).
При выполнении
лабораторных работ студенты могут
использовать как среднюю абсолютную
ошибку, так и среднюю квадратичную.
Какую из них применять указывается
непосредственно в каждой конкретной
работе (или указывается преподавателем).
Обычно если число
измерений не превышает 3 – 5, то
можно использовать среднюю абсолютную
ошибку. Если число измерений порядка
10 и более, то следует использовать более
корректную оценку с
помощью средней квадратичной ошибки
среднего (формулы 5 и 6).
Учет систематических ошибок.
Увеличением числа
измерений можно уменьшить только
случайные ошибки опыта, но не
систематические.
Максимальное
значение систематической ошибки обычно
указывается на приборе или в его паспорте.
Для измерений с помощью обычной
металлической линейки систематическая
ошибка составляет не менее 0,5 мм; для
измерений штангенциркулем –
0,1 – 0,05 мм;
микрометром – 0,01 мм.
Часто в качестве
систематической ошибки берется половина
цены деления прибора.
На шкалах
электроизмерительных приборов указывается
класс точности. Зная класс точности К,
можно вычислить систематическую ошибку
прибора ∆Х по формуле
где К – класс
точности прибора, Хпр – предельное
значение величины, которое может быть
измерено по шкале прибора.
Так, амперметр
класса 0,5 со шкалой до 5А измеряет ток с
ошибкой не более
Среднее значение
полной погрешности складывается из
случайной и систематической
погрешностей.
Ответ с учетом
систематических и случайных ошибок
записывается в виде
Погрешности косвенных измерений
В физических
экспериментах чаще бывает так, что
искомая физическая величина сама на
опыте измерена быть не может, а является
функцией других величин, измеряемых
непосредственно. Например, чтобы
определить объём цилиндра, надо измерить
диаметр D и высоту h, а затем вычислить
объем по формуле
Величины D и h будут измерены с
некоторой ошибкой. Следовательно,
вычисленная величина
V
получится также с некоторой ошибкой.
Надо уметь выражать погрешность
вычисленной величины через погрешности
измеренных величин.
Как и при прямых
измерениях можно вычислять среднюю
абсолютную (среднюю арифметическую)
ошибку или среднюю квадратичную ошибку.
Общие правила
вычисления ошибок для обоих случаев
выводятся с помощью дифференциального
исчисления.
Пусть искомая
величина φ является функцией нескольких
переменных Х,
У, Z…
φ(Х,
У, Z…).
Путем прямых
измерений мы можем найти величины
,
а также оценить их средние абсолютные
ошибки
…
или средние квадратичные ошибки Х,
У,
Z…
Тогда средняя
арифметическая погрешность
вычисляется по формуле
где
— частные
производные от φ по
Х, У, Z. Они
вычисляются для средних значений
…
Средняя квадратичная
погрешность вычисляется по формуле
Пример.
Выведем формулы погрешности для
вычисления объёма цилиндра.
а) Средняя
арифметическая погрешность.
Величины
D и h
измеряются соответственно с ошибкой
D
и h.
Погрешность
величины объёма будет равна
б) Средняя
квадратичная погрешность.
Величины
D и h
измеряются соответственно с ошибкой
D, h.
Погрешность
величины объёма будет равна
Если формула
представляет выражение удобное для
логарифмирования (то есть произведение,
дробь, степень), то удобнее вначале
вычислять относительную погрешность.
Для этого (в случае средней арифметической
погрешности) надо проделать следующее.
1. Прологарифмировать
выражение.
2. Продифференцировать
его.
3. Объединить
все члены с одинаковым дифференциалом
и вынести его за скобки.
4. Взять выражение
перед различными дифференциалами по
модулю.
5. Заменить
значки дифференциалов d
на значки абсолютной погрешности .
В итоге получится
формула для относительной погрешности
Затем,
зная ,
можно вычислить абсолютную погрешность
=
Пример.
Аналогично можно
записать относительную среднюю
квадратичную погрешность
Правила
представления результатов измерения
следующие:
-
погрешность должна
округляться до одной значащей цифры:
правильно = 0,04,
неправильно —
= 0,0382;
-
последняя значащая
цифра результата должна быть того же
порядка величины, что и погрешность:
правильно
= 9,830,03,
неправильно —
= 9,8260,03;
-
если результат
имеет очень большую или очень малую
величину, необходимо использовать
показательную форму записи — одну и ту
же для результата и его погрешности,
причем запятая десятичной дроби должна
следовать за первой значащей цифрой
результата:
правильно —
= (5,270,03)10-5,
неправильно —
= 0,00005270,0000003,
= 5,2710-50,0000003,
=
= 0,0000527310-7,
= (5273)10-7,
= (0,5270,003)
10-4.
-
Если результат
имеет размерность, ее необходимо
указать:
правильно – g=(9,820,02)
м/c2,
неправильно – g=(9,820,02).
Соседние файлы в папке Отчеты_Погрешность
- #
- #
- #
- #
- #