Логическая ошибка тавтология является разновидностью логической ошибки

Тавтология (от греч. ταὐτός – тот же самый и λόγος – слово), термин классической формальной логики, означающий формулу (суждение, высказывание), которая остаётся тождественно истинной для любого набора истинностных значений ее переменных. Тождественная истинность такой формулы обусловлена исключительно её логической структурой.

Например, в логике предикатов 1-го порядка любая атомарная формула A вида a  =  a   (где a суть терм (термин)) является тавтологией: если a  =  МАСЛО, то атомарная формула A имеет вид

МАСЛО  =  МАСЛО («Масло масленное»).

Это значение термина «тавтология» было введено Л.Витгенштейном, а позднее сфера его применения была расширена: «тавтологией» стали называть вообще логически истинные формулы классических логических исчислений – законы классической логики. В соответствии с этим термин «тавтология» естественно относить не к «чистым», а к прикладным формальным исчислениям, в которых зафиксирована область изменения переменных (предметная область рассмотрения или универсум), не смотря на то, что тавтология не зависит от того, каков этот универсум.

Почему? Потому что известна область интерпретации абстрактной формулы: вы всегда имеете возможность проверки её тождественной истинности, а не просто выполнимости в какой-то части универсума.

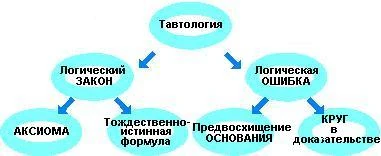
В классической формальной логике термины «тавтология», «логический закон», «тождественно истинная формула» являются синонимами. Одновременно в классической формальной логике термин «тавтология» используется в качестве особой разновидности логической ошибки.

Позиция автора статьи

Витгенштейн, назвав «тавтологией» любую тождественно истинную формулу или логический закон формального исчисления, фактически закрепил уже применяемую десятилетиями многими логиками и философами лексику. Так Г.В.Ф.Гегель применял термин «тавтология» именно в смысле логического закона. Широко известна данная им характеристика для классической формальной логики: «Эта логика ничего кроме формальных тавтологий дать не в состоянии…»

Двусмысленность понятия «Тавтология» в обыденной речи

В обыденной речи (в отличие от, например, текстов юридических законов или инструкций по эксплуатации) достаточно часто используются тавтологичные конструкции, которые, однако, не вводят в заблуждение, так как верификация высказываний осуществляется в «режиме реального времени». В этом случае мы легко различаем, какой смысл «здесь и сейчас» (тавтология это логический закон или логическая ошибка) имеет понятие «Тавтология»:

Тавтология как логическая ОШИБКА:

1) крайний случай логической ошибки «предвосхищение основания» (лат. peti-tio principii), а именно: когда нечто определяется или доказывается тем же самым (лат. idem per idem).

2) “п о р о ч н ы й круг”, т. е. когда тезис обосновывается аргументами, а аргументы обосновываются этим же тезисом.

Например, “Опиум усыпляет потому, что имеет усыпляющую силу”.

В среде формализованного языка (будь то формальная или содержательная логика), очевидно, что такая двусмысленность не допустима, так как верификация суждения осуществляется «наедине с текстом».

Тавтологии диалектической логики

Диалектическими противоположностями в марксизме традиционно являются следующие пары:

сущность и явление, качество и количество, пространство и время, причина и следствие, необходимость и случайность, действительность и возможность, материя и сознание, объект и субъект и др.

Будучи диалектическими противоположностями эти категории образуют диалектически тождественные пары (диады), которые являются элементарными тавтологиями диалектической логики:

СУЩНОСТЬ     ЯВЛЕНИЕ

КАЧЕСТВО     КОЛИЧЕСТВО

ЕДИНСТВО     БОРЬБА

МАТЕРИЯ     СОЗНАНИЕ

ПРИЧИНА     СЛЕДСТВИЕ

НЕОБХОДИМОСТЬ     СЛУЧАЙНОСТЬ

Производительные СИЛЫ     Производственные ОТНОШЕНИЯ

Потребительная СТОИМОСТЬ     Меновая СТОИМОСТЬ

Здесь символ «» суть знак диалектической тождественности.

Тавтологиями Гегель и Маркс в собственных логиках считали также триады. При этом необходимо учитывать, что эти триады никогда не проходили интерсубъективной верификации, а считались эпигонами безусловно истинными как результаты божественного откровения. В марксистско-ленинской диалектике истинной считается единственная гегелевская триада:

При этом не может не возникнуть вопрос: как это в диалектико-материалистическую идеализацию мог попасть как тождественно истинный логический закон из диаметрально противоположной диалектико-идеалистической идеализации? Как это стало возможным? Подумайте!!!

Всё предельно элементарно: гегелевские суждения становятся правдоподобными тогда, когда Гегель забывает о своём Принципе препозиции (ИДЕЯ — первична, МАТЕРИЯ — вторична), а мыслит в соответствие с реальным развитием процесса, т.е. материалистически…

Тавтология в Дианомике

Тавтология (от греч. tauto — то же самое и logos — слово) суть категория Дианомики — логически истинная формула, логический закон. Категория ТАВТОЛОГИЯ суть результат диалектического отрицания категории ПАРАДОКС. В своей экзогенной сети категория ТАВТОЛОГИЯ суть акциденция категории РАЗРЕШЕНИЕ.

Тавтологией в Дианомической логике является любая диада, триада, а также любое суждение, которое корректно образовано из категорий с помощью логических операций и принадлежащее Диалектической сети.

Тавтология и парадокс

Краткий миг торжества… между двумя бесконечностями времени…

Из энциклопедических словарей:

• Википедия

• Философия: Энциклопедический словарь. — М.: Гардарики. Под редакцией А.А. Ивина. 2004.

• БСЭ, 1969-1978

См. также

• Логическая истинность

• Апория

• АНТИНОМИЯ
• Парадокс логический
• Вопрос

• Категории АПОРИЯ и АНТИНОМИЯ, ПАРАДОКС и ТАВТОЛОГИЯ
• Диалектическая логика

Литература

• Л.Витгенштейн. Логико-философский трактат
• Чёрч Α., Введение в математическую логику, пер. с англ., [т.] 1, [M.], 1960, § 15, 19, 23.

• Никлас Луман. Тавтология и парадокс в самоописаниях современного общества.

Ссылки

Обобщить
понятие
— значит
перейти от понятия с меньшим объемом,
но с большим содержанием к понятию с
большим объемом, но с меньшим содержанием.
Например, обобщая понятие «Минис­терство
юстиции Российской Федерации», мы
переходим к понятию «министерство
юстиции»,которое более шире по объёму.

Ограничить
понятие
— значит
перейти от понятия с большим объемом,
но с меньшим содержанием к понятию с
меньшим объемом, но большим содержанием.
Иначе говоря, чтобы ограничить понятие
«юрист», мы переходим к поня­тию
«следователь», которое в свою очередь
можем ограничить, об­разовав понятие
«следователь прокуратуры». Пределом
ограниче­ния понятия является
единичное
понятие.

Обобщение-переход
от единичного к общему,а ограничение-от
общего к единичному.

8. Определение понятий. Правила и ошибки определения.

Логическая
операция, раскрывающая содержание
понятия,
на­зывается определением понятий.

Правила определения:

1. Определение
должно быть соразмерным.

Правило соразмерности
требует, чтобы объем определяемого
по­нятия был равен объему определяющего.
Иначе говоря,
эти понятия должны находиться в отношении
равнообъемности.

2. Определение
не должно заключать в себе круга.

Если при определении
мы прибегаем к другому понятию, кото­рое,
в свою очередь, определяется при помощи
первого, то такое определение содержит
в себе круг. Разновидностью круга в
определении является
тавтология
— ошибочное
определение, в котором определяющее
понятие повто­ряет определяемое.
Тавтология, отличается от круга в
определении меньшей сложностью
построения. Опреде­ляющее понятие
является повторением определяемого.

3. Определение
должно быть ясным.

Оно должно указывать
на известные признаки, не нуждающиеся
в определении и не содержащие
двусмысленности. Если же понятие
определяется через другое понятие,
признаки которого неизвестны и которое
само нуждается в определении, то это
ведет к ошибке, называемой
определением
неизвестного через неизвестное, или
оп­ределением х через
у.

4. Определение
не должно быть отрицательным. Отрицательное
определение не раскрывает определяемого
поня­тия. Оно указывает, чем не является
предмет, не указывая, чем он является.

Ошибки
определения:

а)
широкое определение, когда определяющее
понятие по объему шире, чем определяемое
понятие. Такая ошибка содержится в
следующих определениях: “Лампа — источник
света”.

б)
узкое определение, когда определяющее
понятие по объему уже, чем определяемое
понятие. Например, “совесть — это
осознание человеком ответственности
перед самим собой за свои действия и
поступки” (а перед обществом?);

в)
определение в одном отношении широкое,
в другом — узкое. Например, “бочка — сосуд
для хранения жидкостей”. С одной стороны,
это широкое определение, так как сосудом
для хранения жидкостей может быть и
ведро, а с другой стороны, это узкое
определение, так как бочка пригодна для
хранения и твердых тел, а не только
жидкостей.

9. Деление понятий. Правила деления. Ошибки в делении.

Логическая операция,
раскрывающая объем понятия,
называ­ется делением.

В операции деления
следует различать
делимое
понятие—
объем которого
следует раскрыть,
члены
деления
— соподчиненные
виды, на которые делится понятие, и
основание
деления
— признак,
по которому произво­дится деление.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Тавтология как речевая ошибка

В речи тавтология рассматривается как ошибка.

Термин «тавтология» имеет греческое происхождение. Он возник от слияния двух слов:

• «тавто», что можно перевести как «то же самое»,
• «логос» — «слово».

Тавтология является одной из разновидностей плеоназма.

Примеры плеоназмов:

• прайс-лист цен (по своей сути прайс-лист – это список товаров с указанием цен, слово «прайс» переводится с английского как «цена»);
• своя автобиография (автобиография всегда «своя»; если человек пишет чужую биографию, она не называется «авто»);
• коллеги по работе (слово «коллеги» уже означает общность профессиональной или трудовой деятельности, уточнение «по работе» не требуется).

В тавтологии слова не просто лишние, но еще и однокоренные или повторяющиеся.

Примеры тавтологий:

• подарить в дар;
• объединиться воедино;
• написанное писателем.

Иногда употребление однокоренных слов в словосочетании не является тавтологией; некоторые подобные словосочетания даже стали устойчивыми: «варить варенье», «писать письма», «белое белье».

В риторике не разделяют понятие тавтологии и плеоназма; тавтологию рассматривают более обобщенно, без обязательного требования на неиспользование однокоренных слов.

Тавтология при умелом использовании из ошибки превращается в стилистический прием, создающий образность, эмоциональность и выразительность художественного произведения.

Примеры тавтологий в пословицах и поговорках:

• Дружба дружбой, а служба службой.
• Без вины виноватый.

Иногда тавтологии приобретают дополнительный смысл, определяемый контекстом.

Логические законы как тавтологии

Логические законы представляют собой важный элемент механизма мышления, что определяет их неразрывную связь с другими элементами этого механизма, и в первую очередь – с понятием логического следования, центральным понятием логики как науки. В современной логике эта связь выражается следующим образом: доказать утверждение – это значит показать, что оно логически следует из других утверждений, определенно истинных. Логическое следование заключения из принятых посылок определяется логическими законами. Если нет логического закона, разрушается логическое следование и сам принцип доказательства.

Все логические законы представляют собой логические тавтологии. Если заменить в формуле, представляющей закон, переменные на любые постоянные выражения (подходящей категории), эта формула станет истинным высказыванием:

• закон тождества («если А, то А»): «Если светит солнце, то светит солнце», «Если сейчас зима, то сейчас зима», «Если я иду, значит, я иду»;
• закон исключенного третьего («А или не-А»): «Сейчас идет дождь или не идет дождь», «Два плюс два равно два или два плюс два не равно два»;
• закон противоречия («Неверно, что А и не-А»): «Неверно, что дважды два четыре и дважды два не четыре»;
• закон двойного отрицания («Если неверно, что А неверно, то А верно»): «Если неверно, что сейчас не идет дождь, то сейчас идет дождь».

Все полученные подстановкой сложные высказывания истинны. Они не зависят от рассматриваемой предметной области.

Тавтологический характер логических законов может стать отправной точкой для спекуляций. Тавтология не дает нам новой информации. Так, из высказывания «Сейчас идет дождь или не идет дождь» нельзя понять, какая погода на улице и нужно ли брать с собой зонт. Тавтологию нельзя рассматривать как описание реального положения вещей, поскольку она совместима с любой ситуацией; тавтологию нельзя опровергнуть. Эти специфические особенности логической тавтологии послужили основанием для предположения об отсутствии связи между законами логики и действительностью. Однако подобное предположение неверно. Дело в том, что законы логики занимают «исключительное положение» среди всех высказываний. Они являются априорными, известными до любого опыта истины. Они не бессмысленны – но при том не имеют содержательного смысла; они не могут быть ни подтверждены, ни опровергнуты эмпирическим путем.

Если бы законы логики не несли никакой информации, они бы по своей сути отличались от других научных законов (которые описывают действительность, сообщают какие-то сведения о ней). Основой мысли об информационной пустоте законов логики является узость толкования опыта, который может подтвердить или опровергнуть научный закон. Опыт нельзя сводить к изолированным, фрагментарным ситуациям и фактам. Такого опыта недостаточно для того, чтобы судить об истинности теоретических обобщений, имеющих абстрактный характер и опирающихся на систематический, совокупный опыт. Даже в естественных науках – физике, биологии – нельзя обосновать закон простой ссылкой на наблюдаемые факты. Тем более нельзя это сделать для законов логики, имеющих большую степень абстракции. Законы логики черпают свое обоснование из максимально расширенного опыта теоретической мыслительной деятельности. Конечно, за законами логики тоже стоит опыт – как и за остальными научными законами – но это конденсированный опыт, сложившийся за всю историю познания действительности человеком.