Максимальная
динамическая ошибка
– наибольшее
отклонение регулируемой переменной от
заданного значения Узад:
.
(3.1)
В
устойчивой САР максимальным является
первое отклонение. Таким образом,
показатель
характеризует динамическую точность
регулирования [14].
Время
регулирования
tp
–промежуток времени от момента нанесения
возмущающего воздействия до момента,
начиная с которого отклонение регулируемой
переменной от установившегося значения
становится и остается меньше наперед
заданного значения ].
Остаточное
отклонение (остаточная неравномерность)
—
абсолютная статическая ошибка
регулирования, определяемая как разность
между установившимся значением
регулируемой величины и ее заданным
значением:
=Ууст
– Узад.
(3.2)
Показатель
характеризует точность регулирования
в статическом режиме [5].
Во
всех системах регулирования обязательно
имеется статическая ошибка. Ее можно
уменьшать путем увеличения общего
коэффициента усиления регулятора.
Однако она все равно остается, так как
увеличение коэффициента усиления
регулятора всегда ограничено.
Причиной
статической ошибки системы регулирования
является то, что в равновесном состоянии
регулятора положение регулирующего
органа жестко связано с величиной
регулируемой величины [6].
Система
регулирования, которая по принципу
своего действия обладает статической
ошибкой, называется статической
системой, а
регулятор в этом случае называется
статическим
регулятором.
Статический регулятор осуществляет
следующий закон регулирования:
y
= kрегх,
(3.3)
где
х
– отклонение регулируемой величины, у
– регулирующее воздействие регулятора
на объект.
Система
автоматического регулирования, не
обладающая статической ошибкой,
называется астатической
системой автоматического
регулирования,
а регулятор называется астатическим
регулятором [3].
3.2. Критерии устойчивости сар
Понятие
устойчивости САР связано с способностью
системы возвращаться в состояние
равновесия после исчезновения внешних
сил, которые вывели ее из этого состояния.
Устойчивость
систем автоматического управления
является одним из важнейших условий их
работоспособности, так как устойчивость
включает в себя требование затухания
переходных процессов во времени.
Очевидно, что система с расходящимся
процессом была бы неработоспособной.
Рассмотрим
дифференциальное уравнение движения
линеаризованной системы автоматического
регулирования, записанное для регулируемой
величины у(t)
при наличии управляющего воздействия
g(t)
и при равенстве нулю возмущающих
воздействий (см. формулу (2.4)):
.(3.4)
Процесс
регулирования определяется решением
дифференциального уравнения, как сумма
двух решений – частного решения
неоднородного уравнения (3.4)
с правой частью и общего решения уравнения
(3.4)
без правой части [1].
Характеристическое
уравнение САР имеет вид:
.
(3.5)
Корни
характеристического уравнения (3.5)
определяются только видом левой части
уравнения (3.4).
Постоянные интегрирования определяются
также и видом правой части. Поэтому
быстрота затухания и форма переходного
процесса определяются как левой, так и
правой частями исходного дифференциального
уравнения. Однако поскольку в понятие
устойчивости входит только факт наличия
или отсутствия затухания переходного
процесса (независимо от быстроты
затухания и формы переходного процесса),
то устойчивость линейной системы не
зависит от вида правой части
дифференциального уравнения (3.4)
и определяется только характеристическим
уравнением (3.5)
[13].
Так
как получающаяся при решении линейного
дифференциального уравнения (3.4) формула
переходного процесса содержит составляющие
в виде экспонент от вещественных частей
корней характеристического уравнения
САР (3.5) (см. главу 2), то для того, чтобы
САР была устойчивой и переходный процесс
затухал, необходимо, чтобы вещественные
части корней были отрицательными.
Следовательно,
для устойчивости линейной САР необходимо,
чтобы все корни лежали слева от мнимой
оси, в левой полуплоскости комплексных
чисел. Если хотя бы один корень окажется
справа от мнимой оси, то система будет
неустойчивой. Система будет находиться
на границе устойчивости при наличии:
нулевого корня
();
пары чисто мнимых корней
;
бесконечного корня
().
Во всех трех случаях предполагается,
что все остальные корни имеют отрицательные
вещественные части.
Необходимым
(но не достаточным) условием устойчивости
САР является положительность всех
коэффициентов характеристического
уравнения [7]. Это означает, что система
является неустойчивой, если хотя бы
один из коэффициентов характеристического
уравнения отрицателен. Если все
коэффициенты характеристического
уравнения положительны, то требуются
дополнительные исследования САР на
устойчивость с помощью критериев
устойчивости Гурвица, Михайлова или
Найквиста [3].
В
программе «SAU»
для определения устойчивости САР
используется критерий устойчивости
Гурвица, как наиболее удобный с точки
зрения компьютерной реализации. В методе
Гурвица для характеристического
уравнения (3.5) составляется квадратная
матрица коэффициентов, содержащая n
строк и n
столбцов:

(3.6)
Критерий
устойчивости сводится к тому, что при
а0>0
должны быть больше нуля все n
определителей Гурвица, получаемых из
квадратной матрицы коэффициентов.
Определители
Гурвица составляются по следующему
правилу:
;
;
(3.7)
Последний
определитель включает в себя всю матрицу.
Но так как в последнем столбце матрицы
все элементы, кроме нижнего, равны нулю,
то последний определитель Гурвица
выражается через предпоследний следующим
образом:
.
(3.8)
Однако
в устойчивой системе предпоследний
определитель тоже должен быть
положительным. Поэтому условие
положительности последнего определителя
сводится к условию
,
т.е. к положительности свободного члена
характеристического уравнения [1].
Условия
нахождения системы на границе устойчивости
можно получить, приравнивая к нулю
последний определитель ()
при положительности всех остальных
определителей. Как следует из (3.8),
это условие распадается на два условия:
и
.
Первое
условие соответствует границе устойчивости
первого типа (апериодическая граница
устойчивости), а второе – границе
устойчивости второго типа (колебательная
граница устойчивости).
Для
уравнения второго порядка необходимым
и достаточным условием устойчивости
является положительность всех
коэффициентов характеристического
уравнения. Для уравнений более высокого
порядка необходимо исследование с
помощью составления определителей
Гурвица и проверки их на положительность.
Существенным
недостатком критерия Гурвица является
то, что для уравнений высоких порядков
в лучшем случае можно получить ответ о
том, устойчива или неустойчива система
автоматического регулирования. При
этом в случае неустойчивой системы
критерий не дает ответа на то, каким
образом надо изменять параметры системы,
чтобы сделать ее устойчивой. Это
обстоятельство привело к поискам других
критериев, которые более удобны в
инженерной практике.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Максимальная
динамическая ошибка
– наибольшее
отклонение регулируемой переменной от
заданного значения Узад:
.
(3.1)
В
устойчивой САР максимальным является
первое отклонение. Таким образом,
показатель
характеризует динамическую точность
регулирования [14].
Время
регулирования
tp
–промежуток времени от момента нанесения
возмущающего воздействия до момента,
начиная с которого отклонение регулируемой
переменной от установившегося значения
становится и остается меньше наперед
заданного значения ].
Остаточное
отклонение (остаточная неравномерность)
—
абсолютная статическая ошибка
регулирования, определяемая как разность
между установившимся значением
регулируемой величины и ее заданным
значением:
=Ууст
– Узад.
(3.2)
Показатель
характеризует точность регулирования
в статическом режиме [5].
Во
всех системах регулирования обязательно
имеется статическая ошибка. Ее можно
уменьшать путем увеличения общего
коэффициента усиления регулятора.
Однако она все равно остается, так как
увеличение коэффициента усиления
регулятора всегда ограничено.
Причиной
статической ошибки системы регулирования
является то, что в равновесном состоянии
регулятора положение регулирующего
органа жестко связано с величиной
регулируемой величины [6].
Система
регулирования, которая по принципу
своего действия обладает статической
ошибкой, называется статической
системой, а
регулятор в этом случае называется
статическим
регулятором.
Статический регулятор осуществляет
следующий закон регулирования:
y
= kрегх,
(3.3)
где
х
– отклонение регулируемой величины, у
– регулирующее воздействие регулятора
на объект.
Система
автоматического регулирования, не
обладающая статической ошибкой,
называется астатической
системой автоматического
регулирования,
а регулятор называется астатическим
регулятором [3].
3.2. Критерии устойчивости сар
Понятие
устойчивости САР связано с способностью
системы возвращаться в состояние
равновесия после исчезновения внешних
сил, которые вывели ее из этого состояния.
Устойчивость
систем автоматического управления
является одним из важнейших условий их
работоспособности, так как устойчивость
включает в себя требование затухания
переходных процессов во времени.
Очевидно, что система с расходящимся
процессом была бы неработоспособной.
Рассмотрим
дифференциальное уравнение движения
линеаризованной системы автоматического
регулирования, записанное для регулируемой
величины у(t)
при наличии управляющего воздействия
g(t)
и при равенстве нулю возмущающих
воздействий (см. формулу (2.4)):
.(3.4)
Процесс
регулирования определяется решением
дифференциального уравнения, как сумма
двух решений – частного решения
неоднородного уравнения (3.4)
с правой частью и общего решения уравнения
(3.4)
без правой части [1].
Характеристическое
уравнение САР имеет вид:
.
(3.5)
Корни
характеристического уравнения (3.5)
определяются только видом левой части
уравнения (3.4).
Постоянные интегрирования определяются
также и видом правой части. Поэтому
быстрота затухания и форма переходного
процесса определяются как левой, так и
правой частями исходного дифференциального
уравнения. Однако поскольку в понятие
устойчивости входит только факт наличия
или отсутствия затухания переходного
процесса (независимо от быстроты
затухания и формы переходного процесса),
то устойчивость линейной системы не
зависит от вида правой части
дифференциального уравнения (3.4)
и определяется только характеристическим
уравнением (3.5)
[13].
Так
как получающаяся при решении линейного
дифференциального уравнения (3.4) формула
переходного процесса содержит составляющие
в виде экспонент от вещественных частей
корней характеристического уравнения
САР (3.5) (см. главу 2), то для того, чтобы
САР была устойчивой и переходный процесс
затухал, необходимо, чтобы вещественные
части корней были отрицательными.
Следовательно,
для устойчивости линейной САР необходимо,
чтобы все корни лежали слева от мнимой
оси, в левой полуплоскости комплексных
чисел. Если хотя бы один корень окажется
справа от мнимой оси, то система будет
неустойчивой. Система будет находиться
на границе устойчивости при наличии:
нулевого корня
();
пары чисто мнимых корней
;
бесконечного корня
().
Во всех трех случаях предполагается,
что все остальные корни имеют отрицательные
вещественные части.
Необходимым
(но не достаточным) условием устойчивости
САР является положительность всех
коэффициентов характеристического
уравнения [7]. Это означает, что система
является неустойчивой, если хотя бы
один из коэффициентов характеристического
уравнения отрицателен. Если все
коэффициенты характеристического
уравнения положительны, то требуются
дополнительные исследования САР на
устойчивость с помощью критериев
устойчивости Гурвица, Михайлова или
Найквиста [3].
В
программе «SAU»
для определения устойчивости САР
используется критерий устойчивости
Гурвица, как наиболее удобный с точки
зрения компьютерной реализации. В методе
Гурвица для характеристического
уравнения (3.5) составляется квадратная
матрица коэффициентов, содержащая n
строк и n
столбцов:

(3.6)
Критерий
устойчивости сводится к тому, что при
а0>0
должны быть больше нуля все n
определителей Гурвица, получаемых из
квадратной матрицы коэффициентов.
Определители
Гурвица составляются по следующему
правилу:
;
;
(3.7)
Последний
определитель включает в себя всю матрицу.
Но так как в последнем столбце матрицы
все элементы, кроме нижнего, равны нулю,
то последний определитель Гурвица
выражается через предпоследний следующим
образом:
.
(3.8)
Однако
в устойчивой системе предпоследний
определитель тоже должен быть
положительным. Поэтому условие
положительности последнего определителя
сводится к условию
,
т.е. к положительности свободного члена
характеристического уравнения [1].
Условия
нахождения системы на границе устойчивости
можно получить, приравнивая к нулю
последний определитель ()
при положительности всех остальных
определителей. Как следует из (3.8),
это условие распадается на два условия:
и
.
Первое
условие соответствует границе устойчивости
первого типа (апериодическая граница
устойчивости), а второе – границе
устойчивости второго типа (колебательная
граница устойчивости).
Для
уравнения второго порядка необходимым
и достаточным условием устойчивости
является положительность всех
коэффициентов характеристического
уравнения. Для уравнений более высокого
порядка необходимо исследование с
помощью составления определителей
Гурвица и проверки их на положительность.
Существенным
недостатком критерия Гурвица является
то, что для уравнений высоких порядков
в лучшем случае можно получить ответ о
том, устойчива или неустойчива система
автоматического регулирования. При
этом в случае неустойчивой системы
критерий не дает ответа на то, каким
образом надо изменять параметры системы,
чтобы сделать ее устойчивой. Это
обстоятельство привело к поискам других
критериев, которые более удобны в
инженерной практике.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Статическая ошибка — регулирование
Cтраница 1
Статическая ошибка регулирования может задаваться в абсолютной величине или в безразмерной: по отношению к номинальному значению регулируемого параметра или к диапазону шкалы вторичного прибора.
[1]
Статическая ошибка регулирования теоретически равна нулю, а практически определяется возможной точностью задания и измерения скорости.
[2]
Статическая ошибка регулирования указывает на величину остаточного отклонения параметра; она нежелательна в любом контуре регулирования.
[3]
Статическая ошибка регулирования получается тем меньше, чем больше коэффициент усиления регулятора.
[5]
Статическая ошибка регулирования системы гармонического компаундирования определяется различием воздействия поля реакции якоря по первой и высшим гармоникам. Снижение напряжения определяется воздействием продольной и поперечной составляющих тока якоря, компаундирующее же действие, то есть увеличение напряжения гармонической обмотки и соответственно тока возбуждения генератора, определяется только продольной составляющей тока якоря. Статическую ошибку регулирования возможно, по-видимому, свести к минимуму соответствующим выбором параметров xd и xq генератора.
[6]
Уменьшение статической ошибки регулирования ( ошибки в установившемся режиме) и увеличение быстродействия системы может быть достигнуто последовательным включением в контур системы автоматического регулирования ( в регулятор, осуществляющий основную обратную связь) безынерционного звена с большим коэффициентом усиления.
[8]
Для устранения статической ошибки регулирования ( остаточного отклонения регулируемой величины) напряжение небаланса, снимаемое с движка реостата Лр, подается на сетку левого триода лампы Лг, где усиливается по величине. Усиленное напряжение затем поступает на вход лампы Л3, в анодную цепь которой включена управляющая обмотка асинхронного конденсаторного двигателя Д-32. Скорость вращения двигателя пропорциональна величине сигнала небаланса. Перемещение движка сопротивления Л2 направлено в ту же сторону, что и движка реостата обратной связи RO. Частота импульсов может изменяться в пределах от 45 в минуту до 40 в час путем изменения положения движка переменного сопротивления Д4, изменяющего время разряда RC-цетш.
[9]
Для уменьшения статической ошибки регулирования иногда рекомендуется установка в приточной камере двух калориферов ( или двух рядов калориферов), соединенных последовательно по воздуху и параллельно по воде. Теплопроизводительность каждого калорифера составляет приблизительно 50 % от общей требуемой. Благодаря этому статическая ошибка выбранного регулятора может быть снижена вдвое, так как регулируется только половина нагрузки. Первый по ходу воздуха калорифер отключается двухпозиционным регулятором, датчик которого установлен на входе наружного воздуха, когда достигается температура, при которой требуется только половина нагрузки — теплопроизводительности. Для определения температуры настройки двухпозиционного регулятора требуется провести дополнительные несложные расчеты.
[10]
Говоря о статической ошибке регулирования, считают, что после каждого изменения нагрузки или после отклонения от заданного режима работы, которое вызывается другими причинами, снова устанавливается постоянная скорость вращения вала, пусть не та, что была раньше, но постоянная, и остается дальше неизменным положение всех элементов регулятора.
[11]
Что называется статической ошибкой регулирования.
[12]
При этом условии статическая ошибка регулирования может быть сведена до весьма малой величины.
[13]
Теоретически при kpoo статическая ошибка регулирования становится равной нулю.
[14]
Страницы:
1
2
3
4
5
Демьян Бондарь
Эксперт по предмету «Автоматизация технологических процессов»
преподавательский стаж — 5 лет
Задать вопрос автору статьи
Качество систем управления в переходном режиме
Определение 1
Качество системы управления – это комплексная оценка работы системы управления в зависимости от ее назначения.
Самыми распространенными показателями качества системы в переходном процессе являются:
- Интегральные критерии.
- Статическая ошибка регулирования.
- Степень колебательности.
- Динамическая ошибка регулирования.
- Время регулирования.
- Степень устойчивости.
Статическая ошибка регулирования представляет собой разность между установившемся значением регулируемого параметра и его заданным значением. Динамическая ошибка регулирования равняется наибольшему отклонению регулируемой величины от ее установившегося значения. Время регулирования определяется, как время, за которое разность между текущим значением регулируемого параметра и его заданным значением становится меньше допустимого отклонения. Степень устойчивости автоматической системы управления характеризует запас устойчивости в плоскости корней характеристического уравнения и равняется расстоянию до оси ближайшего корня. Данный критерий характеризует интенсивность затухания наиболее медленно затухающей неколебательной составляющей переходного процесса.

Подработка для студентов
Начни работу по профессии и зарабатывай первые деньги еще будучи студентом
Найти стажировку
Степень колебательности равняется минимальному модулю отношения действительной и мнимой частей корня, то есть:
Рисунок 1.
Если в плоскости корней характеристического уравнения устойчивой системы провести из начала координат два луча (как показано на рисунке ниже) таким образом, чтобы одна пара корней находилась на данных лучах, а остальные лежали слева от них, то тангенс угла, который заключен между лучами и мнимой осью, равный отношению действительной и мнимой частей корней, лежащих на лучах АОВ, является степенью колебательности системы.
Рисунок 2. График. Автор24 — интернет-биржа студенческих работ
«Качество систем управления в установившемся и переходном режимах» 👇
Степень затухания является количественной оценкой интенсивности затухания колебательного процесса:
Рисунок 3.
Между степенью затухания и степенью колебательности существует однозначная зависимость:
Рисунок 4.
Степень затухания может изменяться в пределах от 0,1 до 1, а степень колебательности от 0 до бесконечности. В отличии от прямых показателей интегральные критерии дают обобщенную оценку качества системы, они делятся на:
- линейный интегральный критерий,
- модульные интегральные критерии,
- квадратичный интегральный критерий,
- обобщенные интегральные критерии.
Качество системы управления в установившемся режиме
Определение 2
Установившийся режим – это режим, параметры которого не изменяются во времени или меняются в соответствии с периодическим законом.
Рассмотрим схему одноконтурной системы, которая представлена на рисунке ниже.
Рисунок 5. Схема одноконтурной системы. Автор24 — интернет-биржа студенческих работ
Рассматриваемая схема может быть упрощена следующим образом.
Рисунок 6. Упрощенная схема. Автор24 — интернет-биржа студенческих работ
Для того, чтобы согласовать сигналы u3(t) и uoc(t) надо подобрать одинаковые передаточные функции Wбз(р) и Wби(р), поэтому должно выполняться следующее равенство:
$Wбз(р) = Wби(р)$
С учетом представленного выше равенства схему рассматриваемой системы можно представить в следующем виде.
Рисунок 7. Схема системы. Автор24 — интернет-биржа студенческих работ
В этом случае ошибка регулирования входит в формулу для определения сигнала рассогласования:
$ΔU(р) = Δ(р) WБИ(р)$
Ошибка δ(t) зависит от величины параметров, задающего и возмущающего воздействия, таким образом ее значение может быть выражено как сумма ошибок данных воздействий:
$δ(t) =δy(t) + δf(t)$
Передаточные функции выражаются следующим образом:
Рисунок 8.
Рисунок 9.
Передаточная функция разомкнутого контура выражается следующим образом
$Wрк (р) =WБИ(р) WБУ (р) WОУ(р)$
Исходя из представленных выше выражений величина изображения ошибки определяется следующим образом:
Рисунок 10.
Существую типовые законы оценки установившегося режима, установленные условиями:
- Возмущающее и задающее воздействия не изменяются во времени и постоянны, то есть — yз(t), f (t) = const.
- Изменения в системе происходят с постоянной скоростью, то есть — yз (t) = a t и f (t) = const.
- Изменения в системе происходят с постоянным ускорением, то есть — y(t) = b t2/2и f (t) = const.
- Изменения в системе происходят по гармоническому закону, то есть — yз (t) = y0 sin(ω t) и f (t) = const.
Определение 3
Статическая ошибка – это значение ошибки регулирования при постоянной величине входного воздействия.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Глава 8. Типовые законы регулирования. Одноконтурные САР
8.1. Основные типы автоматических регуляторов
Регулятор на основе усилительного звена называется П-регулятором (пропорциональный). Его положительной характеристикой является высокое быстродействие: при отклонении регулируемой величины от заданного значения регулятор выдает регулирующее воздействие, пропорциональное величине отклонения x, что обеспечивает быструю компенсацию возмущения. Существенным недостатком П-регулятора является наличие статической ошибки в переходном процессе АСР с П-регулятором (рис. 37). Статическая ошибка возникает потому, что у П-регулятора между регулируемой величиной x и регулирующим воздействием xр существует зависимость, однозначно определяемая коэффициентом K. Поэтому генерировать регулирующее воздействие xр для компенсации возмущения xв П-регулятор может только путем изменения регулируемой величины x, что и создает статическую ошибку.
Регулятор на основе интегрирующего звена (48) называется И‑регулятором:
Если xвых усилительного звена (П-регулятор) однозначно определяется величиной правой части уравнения, что является причиной возникновения статической погрешности в АСР с П-регулятором, то правая часть уравнения (48) интегрирующего звена (И-регулятор) определяет не величину, а скорость изменения xвых. Величина xвых будет изменяться до тех пор, пока правая часть уравнения (48) не станет равна нулю, т. е. пока регулируемая величина x при наличии возмущения xв не вернется к заданному значению. Следовательно, в АСР с И-регулятором не возникает статическая погрешность.
Однако у И-регулятора имеется свой недостаток сравнительно с П-регулятором: в случае возникновения возмущения регулирующее воздействие П-регулятора меняется быстрее, чем у И-регулятора с его конечной скоростью, что замедляет процесс компенсации возмущения и ухудшает критерии качества регулирования (рис. 40).
Рис. 40. Переходные процессы в АСР с П- и И-регуляторами
Таким образом, П-регулятор обеспечивает высокое быстродействие (что уменьшает динамическую ошибку), но не может обеспечить при наличии возмущения заданное значение регулируемой величины (статическая ошибка). И-регулятор, наоборот, не создает статическую ошибку, но вследствие относительно медленного изменения xр имеет большую динамическую ошибку.
Сравнивая характеристики П- и И-регуляторов можно сделать вывод: если включить усилительное и интегрирующие звенья параллельно, то автоматический регулятор будет лишен указанных недостатков. Такой регулятор называется ПИ-регулятором (рис. 41).
Рис. 41. Принципиальная схема АСР с ПИ-регулятором
Действительно, быстродействие ПИ-регулятора обеспечивает усилительное звено, а статическую ошибку снимает интегрирующее звено. Для управления производственными процессами чаще всего используются ПИ-регуляторы.
Кривая разгона идеального ПИ-регулятора показана на рис. 42 .
Уравнение ПИ-регулятора при нулевых начальных условиях имеет вид:

Отношение коэффициентов Kp1/Kp определяет степень влияния интегрирующей части, и его обратная величина называется временем изодрома Tи.

Время изодрома – это время, в течение которого интегрирующее звено изменяет регулирующее воздействие xр ПИ-регулятора на величину Dxр, равную предварительному изменению Dxр усилительного звена (рис. 42). Поэтому иногда время изодрома называют временем удвоения.
Рис. 42. График кривой разгона идеального ПИ-регулятора:
а – скачкообразное изменение входного воздействия x;
б – реакция (кривая разгона) ПИ-регулятора xр
Уравнение ПИ-регулятора можно записать как
откуда передаточная функция
Амплитудно-фазовая характеристика:

В том случае, если рассмотренные регуляторы не обеспечивают требуемое качество регулирования, необходимо увеличить интенсивность процесса компенсации возмущения. Этого можно достигнуть увеличением регулирующего воздействия, которое в свою очередь определяется коэффициентом усиления автоматического регулятора Kp
. Однако ниже будет показано, что увеличение коэффициента усиления регулятора в АСР приводит к тому, что в системе начинают генерироваться незатухающие колебания.
В связи с этим представляет интерес рассмотреть алгоритм, который реализует дифференцирующее звено.
Входной величиной любого регулятора является кривая разгона регулируемой величины (рис. 27), которая определяется величиной возмущения и передаточной функцией объекта регулирования (9). В свою очередь, регулирующее воздействие xp (рис. 27) определяется кривой разгона x и передаточной функцией регулятора.
На рис. 43 показана реакция дифференцирующего звена (Д‑регулятора) на входное воздействие в виде кривой разгона в соответствии с уравнением (51).
Рис. 43. Реакция дифференцирующего звена на кривую разгона
а –изменение входного воздействия x в виде кривой разгона;
б – реакция xр дифференцирующего звена
Из рис. 43,а следует, что дифференцирующее звено обеспечивает большее регулирующее воздействие в начале переходного процесса. Это означает, что дифференцирующий регулятор активно компенсирует возмущение и исключает возникновение незатухающих колебаний.
Если включить дифференцирующее звено параллельно ПИ‑регулятору (рис. 44), то получим ПИД-регулятор, обеспечивающий интенсивную компенсацию возмущений. При этом недостаток дифференцирующего звена (при Хвх = const, Хвых = 0 ) компенсируется усилительным и интегрирующим звеньями.
Рис. 44. Принципиальная схема АСР с ПИД-регулятором
На рис. 45 показана кривая разгона ПИД-регулятора.
Рис. 45. Кривая разгона ПИД-регулятора
На рис. 46 показаны переходные процессы на с различными регуляторами. ПИД-регулятор уменьшает динамическую ошибку сравнительно с ПИ-регулятором на 25–30%. Также можно объединить дифференцирующее звено с усилительным звеном и улучшить показатели П-регулятора, получив ПД-регулятор.

Все пять типов рассмотренных автоматических регуляторов имеют общую особенность своего функционирования – обеспечивают стабилизацию регулируемой величины после окончания переходного процесса.
8.2. Критерии качества регулирования
Качество процесса регулирования в АСР характеризуют следующие показатели (критерии) (рис. 16):
Рис. 16. Показатели качества регулирования:
1 – переходной процесс без статической ошибки;
2 – переходной процесс со статической ошибкой
1. Максимальное отклонение в процессе регулирования от заданного значения (динамическая ошибка) ΔХдин.
2. Статическая ошибка ΔХст — возможные отклонения от заданного значения по окончании переходного процесса при использовании некоторых типов регуляторов (подробнее такие АСР рассмотрены ниже).
3. Длительность переходного процесса Тр – период времени с момента начала отклонения регулируемого параметра от задания до возвращения его к заданному значению с определенной степенью точности регулирования ±Δ.
Например, если ±Δ=±25%, это означает, что для заданного значения температуры в 100 °С процесс регулирования будет завершен при достижении диапазона (100 ± 2,5) °С.
4. Степень затухания показывает характер затухания переходного процесса регулирования:
Для того, чтобы переходный процесс затухал за 2 ¸ 3 периода колебаний, степень затухания должна быть равна

5. Степень колебательности процесса m определяет характер колебательности процесса и равна отношению действительной части корня характеристического уравнения к коэффициенту при его мнимой части. Степень колебательности связана со степенью затухания следующим соотношением:
6. Интегральный квадратичный критерий – критерий, определяющий площадь под кривой переходного процесса, возведенной в квадрат (рис. 17):
Уменьшение интегрального критерия соответствует ускорению процесса регулирования.
Рис. 17. Интегральный квадратичный критерий качества регулирования
Однако все приведенные шесть критериев качества не определяют величину потерь производства при отклонениях регулируемой величины от оптимального значения в переходных процессах регулирования. Для определения таких потерь можно использовать экономический критерий.
7. Экономический критерий рассмотрим на примере, регулирования температуры химического реактора θ, когда степень превращения Q в реакторе определяется температурой (рис. 18а).
Разделим переходной процесс на равные интервалы времени Δt и запишем значения θ
в этих точках по графику (18, б). На графике (18, а) для этих температур определим уменьшение степени превращения вследствие отклонения от оптимального режима, а затем сделаем расчет потерь исходных продуктов для каждого интервала Δθ, суммируем эти потери для всего переходного процесса и представим потери в денежном выражении.
Рис. 18. Экономический критерий качества регулирования:
а – зависимость степени превращения Q от температуры θ;
б – переходный процесс регулирования температуры
Совместно со специалистом по технологии или по его заданию необходимо определить, какой из указанных критериев для рассматриваемой АСР является превалирующим, и задать максимально допустимую величину этого критерия, т. е. определить, какое качество регулирования должна обеспечить проектируемая АСР.
8.3. Выбор закона регулирования
При выборе регулятора следует определиться с группой регулирующих устройств – непрерывного, релейного или импульсного действия. Такой выбор ориентировочно может быть сделан по величине отношения запаздывания к постоянной времени объекта τ/Tоб:
· при отношении τ/Tоб меньше 0.2 целесообразно использовать регулятор релейного действия;
· если отношение τ/Tоб от 0.2 до 1.0, то нужно использовать регулятор непрерывного действия;
· при отношении τ/Tоб больше единицы можно использовать регулятор импульсного действия, или специальные регуляторы, например, регулятор («предиктор») Смита.
Затем необходимо определиться с типом регулятора, т.е. выбрать определенный закон регулирования: П-, И-, ПИ-, ПД- или ПИД-закон
8.4. Методы расчета одноконтурных САР
Как указывалось выше, качество автоматического регулирования определяется свойствами системы в целом, т. е. суммарными свойствами объекта и регулятора. Поскольку объект обычно является неизменяемой частью системы, то обеспечить определенные свойства системы, а следовательно и заданное качество регулирования, можно соответствующим подбором свойств автоматического регулятора, что зависит от параметров его настройки. В свою очередь, параметры настройки являются коэффициентами передачи в уравнении автоматического регулятора.
Таким образом, параметры настройки автоматического регулятора определяются свойствами объекта регулирования, т. е. величинами τоб, Тоб, Коб.
8.4.1. Расчет по «приближенным» формулам
Приближенные формулы для расчета параметров настройки автоматических регуляторов (Kр – коэффициент усиления; Tи – время изодрома; Тд – время дифференцирования) сведены в следующую таблицу:
Таблица 8.1. Формулы для приближенного расчета
параметров настройки регуляторов

Формулы сгруппированы в столбцы в зависимости от характера переходного процесса, который желательно получить, используя рассчитанный таким образом регулятор: апериодический или с перерегулированием в 20 %. В формулы входят следующие свойства объекта регулирования: Коб – коэффициент усиления; Тоб – постоянная времени; τоб – время запаздывания (полного).
Рис. 53. Кривые разгона:
1 – фактическая кривая разгона промышленного объекта;
2 – аппроксимированная (приближенная) кривая разгона
Необходимо отметить, что для пневматических регуляторов требуется определять не Kp, а диапазон дросселирования:
Рассмотрим методику более точного определения параметров настройки на примере расчета наиболее «популярного» регулятора – ПИ-регулятора.
8.4.2. Метод незатухающих колебаний
(метод Циглера-Никольса)
При использовании метода незатухающих колебаний [6], который иногда также называется по именам авторов методом Циглера-Никольса, поиск оптимальных параметров настройки осуществляется по величине критического коэффициента усиления П-регулятора и величине периода автоколебательного процесса.
Рис. 54. К поиску параметров настройки методом Циглера-Никольса
Расчет параметров настройки регуляторов проводится в два этапа.
1. На исследуемом объекте устанавливается П-регулятор и, последовательно увеличивая коэффициент усиления (уменьшая диапазон дросселирования), АСР выводится в режим незатухающих колебаний (автоколебаний на границе устойчивости). При этом фиксируется величина коэффициента усиления П-регулятора Ккрр и период незатухающих автоколебаний Т (рис. 54).
2. На втором этапе по величинам Кркр и Т определяются параметры настройки П-, ПИ- и ПИД-регуляторов:
Метод незатухающих колебаний не требует сложных вычислений, но имеет свои характерные недостатки:
· получить Кркр и Т можно только на действующем объекте, оснащенном АСР с П-регулятором;
· не все объекты химической технологии допускают режим автоколебаний;
· практически трудно уловить момент начала автоколебаний.
Данные недостатки имеют место лишь при настройке регулятора методом Циглера-Никольса непосредственно на действующем объекте. Если заменить реальный объект его математической моделью, данный метод лишается указанных недостатков, кроме того, моделирование позволяет на порядок ускорить процесс поиска параметров настройки. Но для выполнения моделирования требуется достаточно точное математическое описание объекта регулирования, а получить его удается не всегда.
8.4.3. Метод расширенных частотных характеристик
Уравнение ПИ-регулятора (65) или (66):
Передаточная функция ПИ-регулятора:

Знак «минус» указывает, что действие регулятора направлено против возмущения.
Из передаточной функции получаем амплитудно-фазовую характеристику ПИ-регулятора путем замены p на iw:

Так как по формуле Эйлера


с затуханием за три периода
Заменив iw на комплексную переменную (-mw+iw), получаем расширенную амплитудно-фазовую характеристику (РАФХ)Ю

Расширенными такие характеристики называются потому, что они как бы «расширены» по отношению к обычной АФХ (рис. 56).
Предположим, что объект регулирования имеет передаточную функцию второго порядка следующего вида:

Для дальнейшего математического моделирования АСР передаточную функцию необходимо преобразовать:

Рис. 56. АФХ объекта регулирования с самовыравниванием:
1 – обычная; 2 – расширенная
Расширенная амплитудно-фазовая характеристика объекта регулирования при замене p на (-mw+iw) будет иметь вид:



Где Rоб(m,w) -расширенная амплитудно-частотная характеристика объекта; Fоб(m,w) -расширенная фазочастотная харктеристика объекта. Величина 40w в выражении для Fоб (m,w) опеделяет угол в радианах и для пересчета в градусы неоходимо 40w умножить на 57,3
Условием нахождения замкнутой АСР на границе устойчивости является уравнение:

Аналогично, исходным уравнением для получения заданной степени колебательности m, а следовательно, определенной степени затухания y, является соотношение:
Это соотношение двух комплексных чисел возможно в том случае, если произведение модулей РАФХ равно единице, а аргументы (фазы) равны между собой, т. е.

Решая эти уравнения относительно S0 и Kp, получаем:


Обычно принимают степень колебательности m = 0,221, что соответствует степени затухания ψ=0,75 и обеспечивает затухание процесса регулирования примерно за три периода. Тогда

Уравнения для определения параметров настройки ПИ-регулятора можно преобразовать:


Подставляя в приведенные уравнения численные значения частоты w от 0 до значения, когда S0 становится отрицательной величиной, строим на плоскости параметров настройки кривую равной степени колебательности


Пример кривых равной степени колебательности в плоскости параметров настройки ПИ-регулятора показан на рис. 57. Графики процессов регулирования с различными параметрами настройки ПИ-регулятора при m = 0,221 показаны на рис. 58. Все процессы регулирования, показанные на рис. 58, реализованы ПИ-регулятором с параметрами настройки, полученными по кривой равной степени колебательности в точках 1, 2, 3, 4 (рис. 57), и все имеют m = 0,221, т. е. затухают примерно за три периода, но обладают существенно различным характером.
В связи с этим возникает задача определения оптимальных параметров настройки на кривой равной степени колебательности.
Рис. 57. Кривые равной степени колебательности
В качестве критерия оптимальности выбираем продолжительность переходного процесса – время регулирования (т. е. быстродействие АСР) и отсутствие постоянной или врéменной статической ошибки. Это исключает из рассмотрения параметры настройки в точке 4 (параметры настройки П-регулятора) и в точке 3 (врéменная статическая ошибка) (рис. 58).
Рис. 58. Графики процессов регулирования для ПИ-регулятора
с различными параметрами настройки в точках 1, 2, 3 и 4
при степени колебательности m =0,221
Быстродействие автоматического регулятора прежде всего зависит от величины регулирующего воздействия, которое для ПИ-регулятора, как следует из уравнения (65), прямо пропорционально величине коэффициента усиления Kp и обратно пропорционально времени изодрома Tи. Расчеты показывают, что если двигаться по кривой равной степени колебательности вправо, то величина регулирующего воздействия при прочих равных условиях сначала возрастает и достигает максимального значения на кривой равной степени колебательности вблизи ее вершины, когда
а затем начинает уменьшаться в связи с резким увеличением Tи (рис. 57).
Рис. 59. Выбор оптимальных параметров настройки
Таким образом, оптимальные параметры настройки ПИ-регулятора находятся в точке 2 на кривой равной степени колебательности (рис. 59).
Источник
Плютто В. П., Дубровский И. И. Элементы теории управления химико-технологическими процессами и системами. Конспект лекций: Учеб. пособие – М.: РХТУ им. Д. И. Менделеева, 2003. – 127 с.
К системам автоматического регулирования (САР) предъявляются требования не только
устойчивости процессов регулирования. Для работоспособности системы не менее необходимо, чтобы процесс автоматического регулирования осуществлялся при обеспечении определенных показателей качества процесса управления.
Если исследуемая САР является устойчивой, возникает вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям обьекта управления.На практике качество регулирования определяется визуально по графику переходной характеристики. Однако, имеются точные но более сложные математические методы, дающие конкретные числовые значения (которые не рассматриваются в данной методике).
Классификация показателей качества состоит из нескольких групп:
- прямые — определяемые непосредственно по переходной характеристике процесса,
- корневые — определяемые по корням характеристического полинома,
- частотные — по частотным характеристикам,
- интегральные — получаемые путем интегрирования функций.
Прямыми показателями качества процесса управления, определяемые непосредственно по
переходной характеристике являются:
- Установившееся значение выходной величины Yуст,
- Степень затухания ?,
- Время достижения первого максимума tmax,
- Время регулирования tp,
- Ошибка регулирования Ест (статистическая или среднеквадратическая составляющие),
- Перерегулирование у,
- Динамический коэффициент регулирования Rd,
- Показатель колебательности М.
Например, переходная характеристика, снятая на объекте управления при отработке ступенчатого воздействия, имеет колебательный вид и представлена на рис.1.
Рисунок 1 — Определение показателей качества по переходной характеристике
Установившееся значение выходной величины Yуст
Установившееся значение выходной величины Yуст определяется по переходной характеристике,представленной на рис.1.
Степень затухания ?
Степень затухания ? определяется по формуле:
где А1 и А3 — соответственно 1-я и 3-я амплитуды переходной характеристики рис.1.
Время достижения первого максимума tmax
Время достижения первого максимума tmax определяется по переходной характеристике,представленной на рис.1.
Время регулирования tp
Время регулирования tp определяется согласно рис.1 следующим образом:Находится допустимое отклонение Д, например, задано Д = 5%Yуст и строится «зона» толщиной 2 Д(см. рис.1). Время tp соответствует последней точке пересечения Y(t) с данной границей. То есть время,когда колебания регулируемой величины перестают превышать 5 % от установившегося значения.
Настройки регулятора необходимо выбирать так, чтобы обеспечить минимально возможное значение общего времени регулирования, либо минимальное значение первой полуволны переходного процесса.
В непрерывных системах с типовыми регуляторами это время бывает минимальным при так называемых оптимальных апериодических переходных процессах. Дальнейшего уменьшения времени регулирования до абсолютного минимума можно достичь при использовании специальных оптимальных по быстродействию систем регулирования.
Ошибка регулирования Ест
Статическая ошибка регулирования Ест = Ув — Ууст, где Ув — входная величина (см. рис.1).В некоторых САР наблюдается ошибка, которая не исчезает даже по истечении длительногоинтервала времени — это статическая ошибка регулирования Ест. Данная ошибка не должна превышатьнекоторой наперед заданной величины. У регуляторов с интегральной составляющей ошибки в установившемся состоянии теоретическиравны нулю, но практически незначительные ошибки могут существовать из-за наличия зоннечувствительности в элементах системы.
Перерегулирование у
Величина перерегулирования у зависит от вида отрабатываемого сигнала.При отработке ступенчатого воздействия (по сигналу задания) – см. рис.1 величина перерегулирования у определяется по формуле:
где значения величин Ymax и Yуст определяются согласно рис.1.
При отработке возмущающего воздействия, величина перерегулирования у определяется изсоотношения:
где значения величин Xm и X1 определяются согласно рис. 2.
Рисунок 2 — График переходного процесса при отработке возмущения
Динамический коэффициент регулирования Rd
Динамический коэффициент регулирования Rd определяется из формулы:
где значения величин Y1 и Y0 определяются согласно рис. 3.
Рисунок 3 — К понятию динамического коэффициента регулирования
Величина динамического коэффициента Rd характеризует степень воздействия регулятора напроцесс, т.е. степень понижения динамического отклонения в системе с регулятором и без него.
Показатель колебательности М
Показатель колебательности M характеризует величину максимума модуля частотной передаточной функции замкнутой системы (на частоте резонанса) и, тем самым, характеризует колебательные свойства системы. Показатель колебательности наглядно иллюстрируется на рисунке 4.
Рисунок 4 — График модуля частотной передаточной функции замкнутой системы
Условно считается, что значение М=1,5-1,6 является оптимальным для промышленных САР, т.к. вэтом случае у обеспечивается в районе от 20% до 40%. При увеличении значения M колебательность всистеме возрастает.
В некоторых случаях нормируется полоса пропускания системы щп, которая соответствует уровню усиления в замкнутой системе 0,05. Чем больше полоса пропускания, тем больше быстродействие замкнутой системы. Однако при этом повышается чувствительность системы к шумам в канале измерения и возрастает дисперсия ошибки регулирования.
Вид возмущения –
скачек.
Построим
переходной процесс САР (рисунок 18)
Рисунок 18 – Переходной процесс САР с рекомендуемыми
параметрами
Максимальная
динамическая ошибка = 4,53058.
Степень затухания = 0,991192.
Время регулирования = 30,3160.
Переходная
характеристика имеет большое динамическое отклонение, но без перерегулирования.
Выполним
проверку САР на грубость, получим переходной процесс (рисунок 19).
Сплошная – САР с исходным объектом; пунктир – САР с
объектом, у которого коэффициент усиления и запаздывания увеличены на 20%
Рисунок 19 – Проверка САР на грубость
Максимальная
динамическая ошибка = 5,64977.
Степень затухания = 0,923628.
Время регулирования = 56,0560.
По графикам на
рисунке 17 видно, что при увеличении коэффициента усиления и запаздывания на
20% качество ухудшается. Максимальная динамическая ошибка увеличивается на
24,72%, а время регулирования на 25,74 с, переходной процесс становится
колебательным.
Проведем
оптимизацию параметров регулятора методом поиска.
Выбираем
критерий ITAE.
Оптимальные
значения:
Критерий
Кр Ти
1010,4 0,12258 6,8936
Построим
переходной процесс системы с оптимальными параметрами (рисунок 20).
Сплошная – выход САР с исходными параметрами;
пунктир – с оптимальными.
Рисунок 20 – Переходной процесс системы с оптимальными
параметрами
Максимальная
динамическая ошибка = 4,43428.
Степень затухания = 0,939782.
Время регулирования = 26,3120.
Качество
переходного процесса системы в оптимальными параметрами выше чем с исходными.
Уменьшилась динамическая ошибка и вдвое сократилось время регулирования.
3.2.1
Настройка САР с опережающим импульсом. Схема с дифференциатором.
Расчет
параметров дифференциатора:
ПИ-регулятор Wp = Кр[1+1/(Tи*s),
где Кр = 0,03; Ти
= 0,78.
Дифференциатор
Wg = 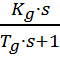
где Кg =
21,261; Тg = 3,84.
Возмущение
на входе объекта (по нагрузке) – единичный скачек.
Построим
переходной процесс (рисунок 21).
Сплошная – выход одноконтурной САР;
пунктир – выход САР с опережающим импульсом.
Рисунок 21 – Переходные процессы САР
Максимальная
динамическая ошибка = 2,06053.
Степень затухания = 0,99501.
Время регулирования = 26,8840.
САР с
опережающим импульсом (схема с дифференциатором) имеет намного меньшую
динамическую ошибку чем одноконтурная САР.
Проверим
САР на грубость (рисунок 22).
Сплошная – выход
Y1 САР с исходным объектом; пунктир – выход Y1 САР с объектом, у которого
коэффициент усиления и запаздывания увеличены на 20%.
Рисунок 22 – Проверка САР на грубость
Максимальная
динамическая ошибка = 2,46921.
Степень затухания = 0,982544.
Время регулирования = 26,312.
При увеличении
коэффициента усиления и запаздывания на 20% наблюдается увеличение
динамической ошибки на 16,6%.
Проведем
оптимизацию параметров регулятора методом поиска.
Оптимальные
параметры:
Критерий
Кр Ти
210,76 0,052712 0,58067
Построим
переходной процесс САР с дифференциатором при оптимальных параметрах (рисунок 23).
Сплошная – выход одноконтурной САР; пунктир – выход
САР с опережающим импульсом; сплошная(низ) – выход САР с опережающим импульсом
при оптимальным параметрах
Рисунок 23 – Переходные процессы САР
Максимальная
динамическая ошибка = 1,55769.
Степень затухания = 0,923489.
Время регулирования = 20,5920.
Здравствуйте, на этой странице я собрала краткий курс лекций по предмету «теория автоматического управления».
Лекции подготовлены для студентов любых специальностей и охватывают предмет «теория автоматического управления ».
В лекциях вы найдёте основные законы, теоремы, формулы, примеры.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Теория автоматического управления (ТАУ) — научная дисциплина, которая изучает процессы автоматического управления объектами разной физической природы. При этом при помощи математических средств выявляются свойства систем автоматического управления и разрабатываются рекомендации по их проектированию. Является составной частью технической кибернетики и предназначена для разработки общих принципов автоматического управления, а также методов анализа (исследования функционирования) и синтеза (выбора параметров) систем автоматического управления (САУ) техническими объектами. wikipedia.org/wiki/Теория автоматического управления
Что такое теория автоматического управления
Теория автоматического управления (ТАУ) — научная дисциплина,
предметом изучения которой являются информационные процессы,
протекающие в системах управления техническими и технологическими объектами. Теория автоматического управления выявляет общие закономерности функционирования, присущие автоматическим системам различной физической природы, и на основе этих закономерностей разрабатывает принципы построения высококачественных систем управления.
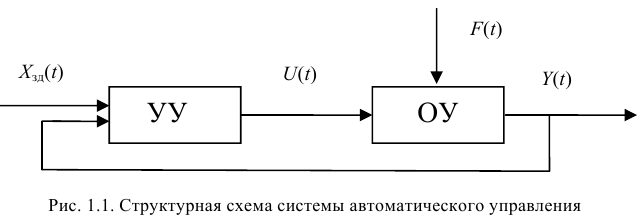
Введение в теорию автоматического управления
Систему автоматического управления условно можно представить состоящей из двух частей: объекта управления (ОУ) и управляющего устройства (УУ) (рис. 1.1).
На вход системы управления подается задающее воздействие 
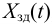
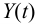
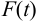
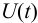
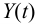
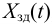
При разработке автоматических систем управления чаще всего ставится задача, заключающаяся в том, чтобы система выполняла свое функциональное назначение, определяемое целыо управления. Иногда может быть поставлена и более сложная задача: разработать автоматическую систему с наилучшими показателями качества. При разработке таких систем используется принцип оптимальности, позволяющий обеспечить наилучшее выполнение цели управления.
Понятия и постановка задачи оптимального управления
Автоматическую систему регулирования, обеспечивающую наилучшие показатели качества при отработке задающих и возмущающих воздействий, называют оптимальной. Оценку достижимости цели в процессе управления объектом, представленную в формализованном виде (аналитической форме), принято называть критерием оптимальности, или целевой функцией.
Разработка наилучшей системы, удовлетворяющей заданным требованиям, представляет собой задачу синтеза оптимальной системы.
Возможны два основных типа задач синтеза оптимальных систем. В задачах первого типа (параметрическая оптимизация) известна структура системы (передаточные функции устройства управления и объекта управления). Необходимо найти оптимальные значения параметров динамической настройки устройства управления (регулятора), при которых обеспечиваются требуемые значения заданного показателя качества. В задачах второго типа структура системы полностью неизвестна и требуется вначале ее определить по исходной динамике объекта, а затем рассчитать параметры динамической настройки устройства управления, чтобы система была оптимальной по показателям качества. На практике обычно задан объект управления, поэтому задача синтеза состоит в определении структуры и параметров динамической настройки оптимального регулятора. Такая задача может быть названа задачей структурно-параметрической оптимизации.
Переменные выхода 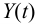
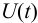
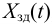
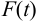
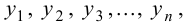
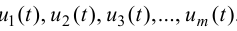
Предположим, что момент 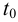
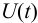
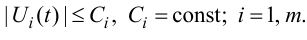
Совокупность ограничений формирует область возможных значений управляющих воздействий. Обозначим эту область символом 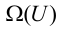
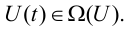
В этом случае управления называются допустимыми и, как правило, являются кусочно-непрерывными функциями. Аналогично компоненты вектора состояния
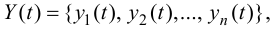
в общем случае так же должны удовлетворять определенным ограничениям, то есть вектор 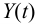
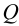
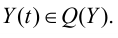
Пусть в области допустимых состояний 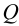
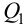
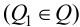
Тогда цель управления заключается в том, чтобы перевести объект из начального состояния 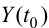
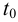
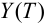
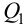
Отметим, что момент 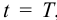
Задача управления заключается в том, чтобы в области допустимых управлений (1.2) подобрать такое управление, при котором будет достигнута цель управления. Иными словами, требуется отыскать такое допустимое управление 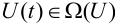
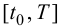
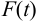
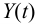
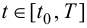
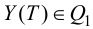
Наиболее типична ситуация, когда задача управления имеет бесконечное число решений, то есть существует бесконечное число допустимых управлений, переводящих объект из начального состояния в конечное в соответствии со всеми введенными ограничениями. В этом смысле все управления, реализующие цель управления, являются равноценными.
Однако к системе управления, как правило, предъявляется ряд требований, не участвующих в формулировке задачи управления, но характеризующих успешность продвижения по пути к цели управления.
Чтобы судить о степени соответствия системы предъявляемым к ней требованиям, вводят в рассмотрение числовые показатели, отражающие качественную сторону процесса движения к цели управления и формирующие понятия качества управления.
Формально качество управления можно описать двояко:
- в форме совокупности показателей качества, например, значений допустимого перерегулирования, времени регулирования, установившихся ошибок при типовых воздействиях и т. п.;
- в форме некоторого обобщенного показателя, определяемого всеми процессами:
(задающее воздействие может быть также многомерным).
При каждом управлении, на котором достигается его цель, качество будет принимать определенное значение. Очевидно, что из числа управлений, реализующих цель, следует выбирать такие, при которых качество будет обеспечено в соответствии с существующими требованиями.
При первом подходе качество управления оценивают совокупностью показателей, по существу представляющих параметры реакции системы на некоторое детерминированное входное воздействие. Такой подход свойственен раннему этапу развития теории автоматического управления (ТАУ), хотя используется и в настоящее время. В этом случае выбор рационального управления заменяется выбором структуры и параметров регулятора, которые обеспечивают показатели качества, не худшие относительно их заданных значений.
При втором подходе качество управления описывают некоторым обобщенным показателем, представляющим собой меру эффективности достижения цели управления средствами конкретного управления 
Обобщенный показатель качества — числовая характеристика, в общем случае зависящая от 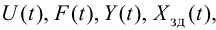
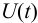
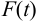
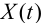
Качество может содержать различный физический смысл и отражать в зависимости от технического назначения объекта такие свойства системы управления, как, например, энергетические затраты на управление, точность поддержания заданного режима работы объекта управления, время достижения цели управления, значение максимальной ошибки в определенном режиме функционирования, качество выпускаемой продукции, затраты сырья или электроэнергии, себестоимость продукции и т. д.
Наиболее часто обобщенный показатель качества представляет функционал, который можно описать в форме следую-щего интегрального соотношения:
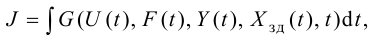
где функция 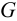
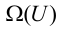
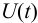
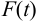
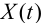
а объект управления переводится из начального состояния 
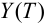
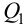
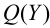
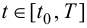
Условие (1.5) в этом случае называют критерием оптимальности, а управление, удовлетворяющее условиям задачи, называют оптимальным.
Решение уравнения ОУ, соответствующее оптимальному управлению и удовлетворяющее цели управления, называют оптимальной траекторией движения ОУ. Систему управления, которая с позиций критерия (1.5) оказывается наилучшей среди всех других систем, называют оптимальной.
Критерии оптимальности систем автоматического регулирования
При разработке оптимальных систем важным моментом является формулировка цели оптимизации, которая математически выражается как требование обеспечения минимума или максимума некоторого показателя качества, называемого критерием оптимальности, или целевой функцией.
Основными критериями качества автоматических систем являются: максимальная точность управления объектом; максимальное быстродействие перехода системы из одного состояния в другое при ограничении управляющего воздействия; минимальные затраты энергии на управление объектом при заданных внешних условиях; минимальная стоимость системы управления при заданном качестве управления объектом и т. д. При этом необходимо иметь в виду, что оптимизация одного из указанных качеств системы управления обычно может приводить к ограничению ее других характеристик. Учет указанных ограничений при оптимизации системы очень важен, поскольку любая система автоматического управления характеризуется ограниченной мощностью, точностью, надежностью, инерционностью и т. д. Каждый из этих критериев является некоторой функцией нескольких переменных, характеризующих систему управления в целом.
При разработке локальных систем управления обычно рассматривают задачу оптимизации по критериям, характеризующим качество функционирования системы (точность и быстродействие), а остальные частные критерии не учитывают. Тогда задача оптимизации сводится к выбору структуры регулятора и параметров его настройки, при которых свойства системы оптимальны, то есть сводится к выбору лучшего варианта из числа возможных.
Каждый из таких вариантов системы характеризуется отклонением 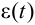
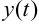
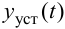
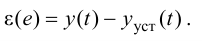
Тогда качество вариантов системы определяют некоторым показателем — численной характеристикой, показывающей, насколько 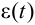
Такие показатели качества можно рассматривать как функциональные выражения, в которых роль независимых переменных играют функции, кривые, векторы, характеризующие варианты системы.
В зависимости от конкретных условий функционирования систем управления обычно рассматривают две задачи оптимизации режимов: динамическую и статическую.
Рассмотрим некоторые типы критериев оптимальности в зависимости от принадлежности к переходному или установившемуся режиму работы системы управления.
В качестве критерия оптимальности может быть принято время переходного процесса:
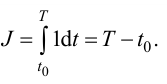
Полученная система управления является оптимальной по быстродействию, если обеспечивается минимум интеграла (1.5) с учетом ограничений координат.
В качестве критерия оптимальности могут быть использованы интегральные оценки качества переходных процессов.
Например, при использовании квадратичной оценки система будет оптимальной, если обеспечивается минимум интеграла
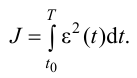
Полученная система управления является оптимальной по точности в динамических режимах при отработке единичного задающего воздействия 
Часто, помимо критерия оптимизации, необходимо учитывать и ограничения, налагаемые на переменные системы. Они могут быть заданы в виде
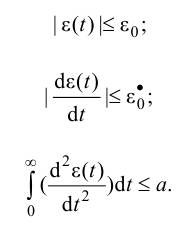
Ограничения (1.1), (2.4) и (2.5) требуют, чтобы отклонения 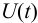
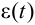
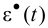
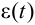
Кроме рассмотренного интегрального критерия, для оптимизации используют и более общие показатели, например:
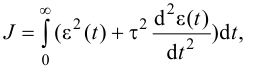
где
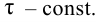
Этот показатель оптимальности эквивалентен в определенном смысле квадратичному показателю оптимальности (2.3) при учете ограничений вида (2.6). Выбор параметров системы так, чтобы минимизировать критерий (2.7), позволяет получить не только оптимальные по быстродействию, но и плавные переходные процессы без значительных колебаний при отработке единичных задающих воздействий.
Особый интерес представляет выбор критерия оптимальности в виде оптимальной передаточной функции системы по задающему воздействию 
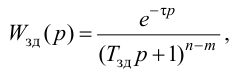
где 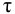
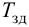
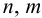
Передаточная функция системы по задающему воздействию (2.8) входит в передаточную функцию оптимального регулятора:
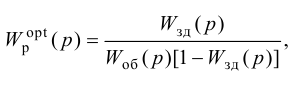
где 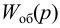
Передаточную функцию оптимального регулятора (2.9) можно представить в виде произведения инверсной передаточной функции объекта регулирования на заданную передаточную функцию разомкнутой системы:
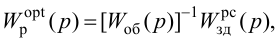
где 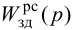
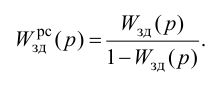
Выбор функционалов, соответствующих критерию оптимальности, представляет собой трудную задачу, поскольку связан с учетом многих конкретных условий, как, например, требований, предъявляемых к системе управления, обоснования максимальной величины регулирующего воздействия, простоты последующего определения структуры и динамической настройки оптимальной системы и т. п.
Экспериментальные методы определения динамических характеристик теплоэнергетических объектов регулирования
Идентификация объектов регулирования с использованием переходных характеристик
При изучении объекта исследования, прежде всего, выбирают входную и выходную переменную. Если определяют динамические характеристики объекта управления, то в качестве входной величины принимают положение регулирующего органа, а в качестве выходной — сигнал измерительного преобразователя, поступающий на вход регулятора. При исследовании замкнутой системы регулирования входное воздействие наносят перемещением задатчика, фиксируя при этом изменение выходной величины — сигнал измерительного преобразователя.
Обработка результатов эксперимента включает в себя целый ряд операций, которые завершаются аппроксимацией переходной характеристики с помощью типовых элементарных звеньев.
Предварительный выбор передаточной функции можно сделать по начальному участку переходной функции (рис. 3.1).
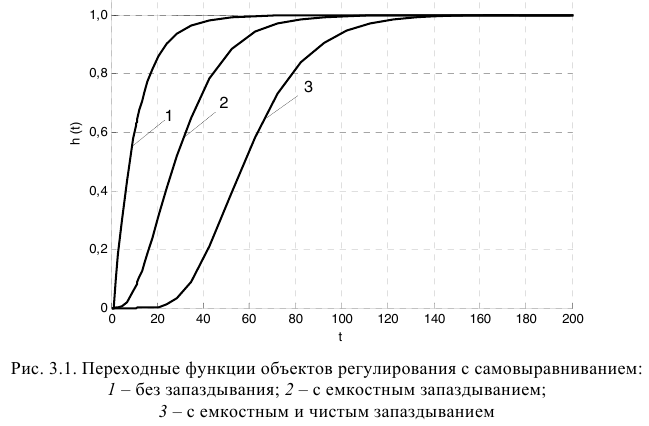
Передаточной функцией 1 (табл. 3.1) аппроксимируют переходные функции, наклон графиков которых в начальный момент времени максимален, то есть переходные функции объектов без запаздывания (кривая 1 на рис. 3.1). Применение такой передаточной функции требует определения наименьшего числа параметров -двух для объектов с самовыравниваиием.
Однако переходные функции большинства промышленных объектов имеют, как правило, вид кривых 2 и 3 (см. рис. 3.1). Для аппроксимации таких переходных функций используют передаточные функции 2 и 3 (см. табл. 3.1).

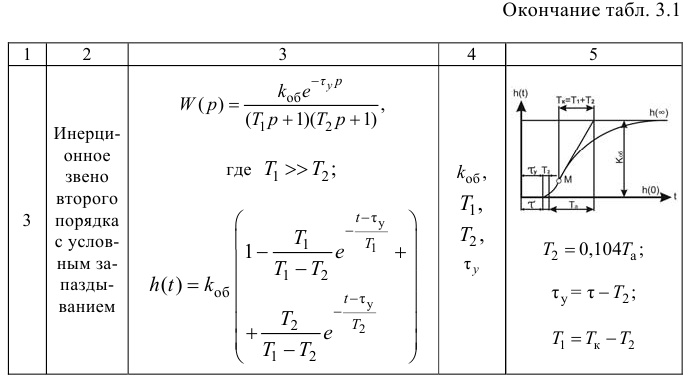
Для объектов с малым емкостным запаздыванием наиболее распространена передаточная функция 2, которой аппроксимируют переходные функции объектов, для которых свойственно только емкостное запаздывание (кривая 2 на рис. 3.1).
Передаточную функцию 3 (см. табл. 3.1) обычно используют для аппроксимации переходных функций объектов с большим запаздыванием, для которых свойственно только емкостное и чистое запаздывание (кривая 3 на рис. 3.1).
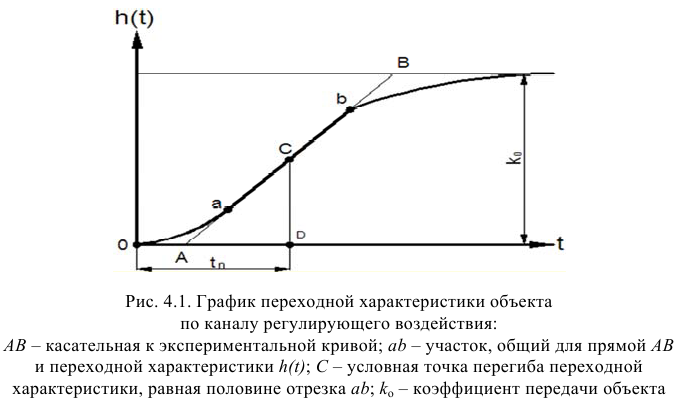
Динамические параметры объекта по его экспериментально снятой переходной характеристике определяют графическими или графоаналитическими методами. При определении динамических параметров объекта вначале проводят касательную к переходной характеристике объекта таким образом, чтобы как можно больше точек прямой и переходной характеристики объекта совпали, затем определяют динамические параметры передаточной функции.
В табл. 3.2 приведены наиболее распространенные методы определения динамических параметров объекта без самовыравиивания и показаны графические построения, выполняемые при их использовании.
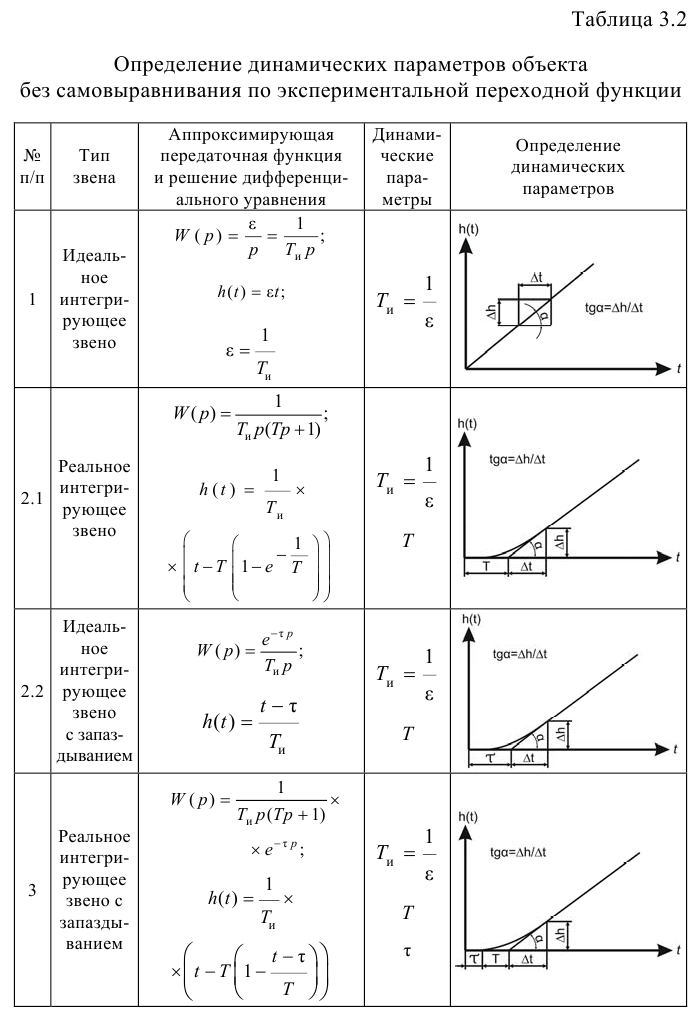
Предварительный выбор передаточной функции можно сделать по начальному участку переходной функции (рис. 3.2).
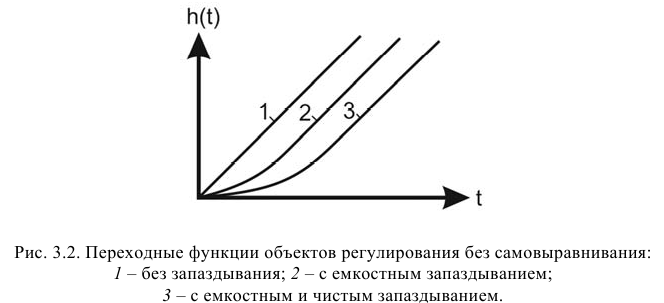
Передаточной функцией 1 (табл. 3.2) аппроксимируют переходные функции, наклон графиков которых в начальный момент времени максимален, то есть переходные функции объектов без запаздывания (кривая 1 на рис. 3.2). Применение такой передаточной функции требует определения наименьшего числа параметров -одного для объектов без самовыравнивания.
Однако переходные функции большинства промышленных объектов без самовыравнивания имеют, как правило, вид кривых 2 и 3 (см. рис. 3.2). Для аппроксимации таких переходных функций используют передаточные функции 2 и 3 (см. табл. 3.2).
Наиболее распространена передаточная функция 2, которой аппроксимируют как переходные функции объектов, для которых свойственно только емкостное запаздывание (кривая 2 на рис. 3.2), так и переходные функции объектов, обладающих емкостным и чистым запаздыванием (кривая 3 на рис. 3.2).
Передаточную функцию 3 (см. табл. 3.2) обычно используют для аппроксимации переходных функций объектов, для которых свойственно только емкостное запаздывание (кривая 2 на рис. 3.2).
Динамические параметры объекта по его экспериментально снятой переходной характеристике определяют графическими или графоаналитическими методами. При определении динамических параметров объекта вначале проводят касательную к переходной характеристике объекта таким образом, чтобы как можно больше точек прямой и переходной характеристики объекта совпали, затем определяют динамические параметры передаточной функции.
Идентификация объектов регулирования с использованием импульсных характеристик
При снятии импульсных характеристик для успешного проведения исследований существенное значение имеет правильный выбор длительности импульса. Чем меньше время импульса, тем ближе экспериментальная временная характеристика к истинной импульсной. Однако при малых значениях длительности импульса обработка результатов становится затруднительной из-за малых отклонений выходной переменной от своих первоначальных значений. Поэтому на практике идут на определенное искажение импульсной характеристики, увеличивая длительность импульса. При снятии импульсных характеристик длительность импульса чаще всего определяют опытным путем в процессе проведения эксперимента.
В основе этого метода лежит определение площадей, ограниченных кривыми изменения входной и выходной величины. Вначале определяют время запаздывания 
Время запаздывания определяют по формуле
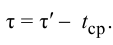
Остальные параметры для объекта с самовыравииванием находят по формулам
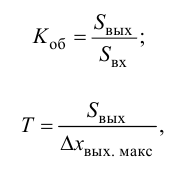
где 
Для объекта без самовыравнивания — по формуле
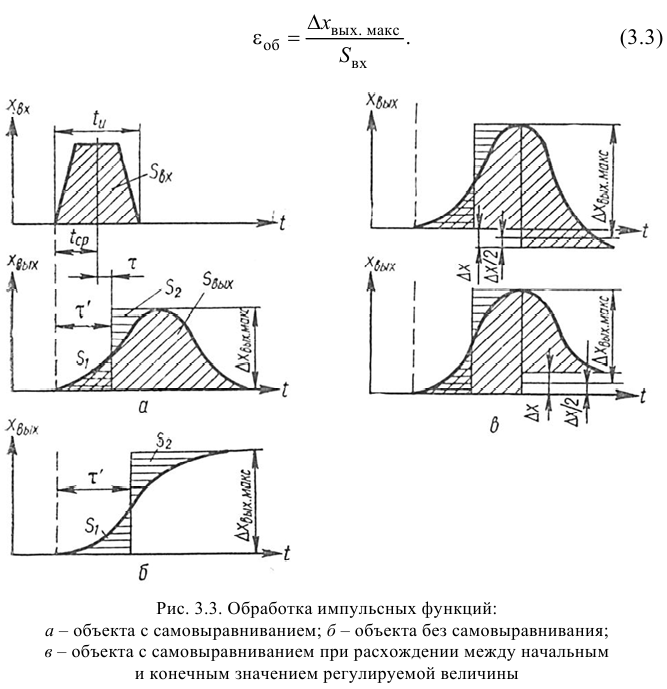
На рис. 3.3, в показана особенность определения 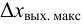
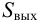
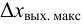
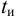
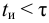
Идентификация объектов регулирования с использованием частотных характеристик
При выборе диапазона частот входного воздействия, прежде всего, учитывают назначение частотных характеристик. Для расчета параметров динамической настройки регулятора наибольшее значение в соответствии с критерием устойчивости Найквиста имеют частоты при фазовых сдвигах, находящихся вблизи 180°. Поэтому при наладке систем автоматического регулирования эксперимент проводят либо на одной частоте 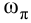
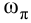
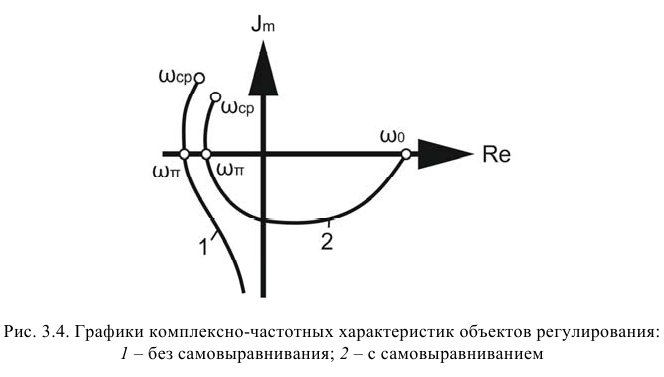
Точку с частотой 
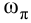
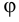
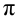
Для этого после достижения установившегося режима работы регулируемого объекта (момент времени 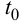
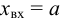
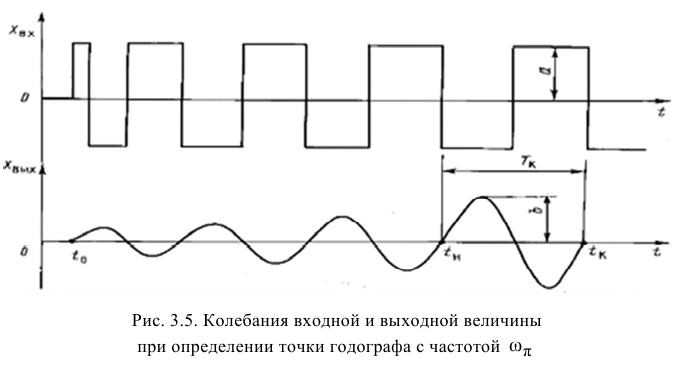
После того как отклонение регулируемой величины под действием этого воздействия станет заметным, регулирующий орган быстро перемещают в противоположную сторону на величину 
Обработку результатов эксперимента начинают с определения 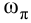
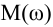
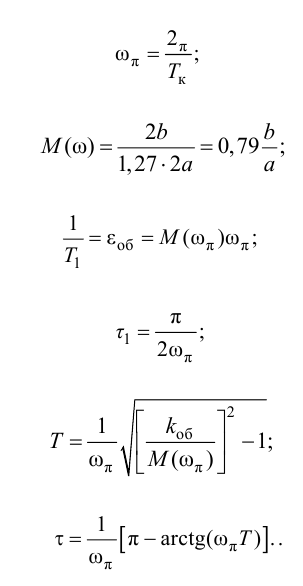
В результате искомая передаточная функция объекта регулирования без самовыравнивания с учетом формул (3.6) и (3.7) примет вид
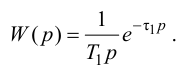
Для объектов с самовыравниванием соответственно с учетом формул (3.8) и (3.9):
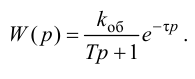
Универсальная методика описания динамики объекта регулирования передаточными функциями различной структуры
При проведении сравнительного анализа различных методов расчета параметров динамической настройки типовых регуляторов зачастую необходимо передаточную функцию объекта регулирования исходной структуры преобразовать в другую структуру, которая используется каким-либо автором для оптимизации динамики типовых регуляторов.
Если исходной является экспериментально снятая реакция объекта на единичный скачок и требуется аппроксимировать динамику объекта регулирования передаточной функцией инерционного звена 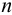
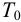
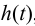
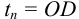
Затем определяют интегральную постоянную времени объекта 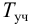
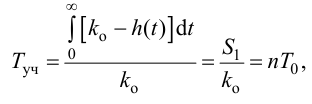
где 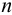
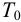
Численное значение 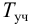
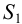
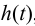
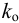
Для модели с 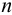
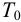
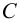
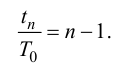
Откуда находят численное значение постоянной времени 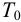
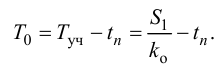
Затем из (4.2) с учетом (4.3) определяют порядок модели объекта регулирования 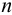
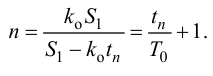
Иногда вместо экспериментальных динамических характеристик объектов регулирования на стадии проектирования объекта используют расчетные методы. Например, если исходными являются характерные параметры пароперегревателя 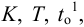
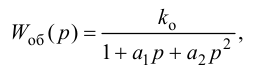
где
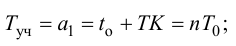
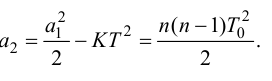
Откуда находят порядок математической модели объекта
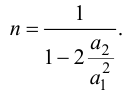
Определив порядок модели передаточной функции объекта регулирования из равенства (4.6), находим постоянную времени 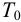
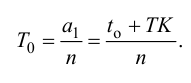
Если аппроксимация динамики объекта регулирования задана передаточной функцией инерционного звена первого порядка с запаздыванием
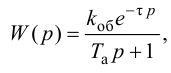
где 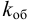
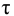
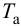
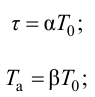
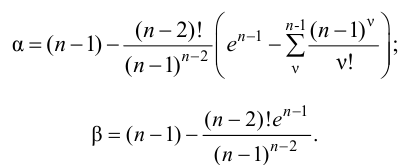
При моделировании переходных процессов систем автоматического регулирования (САР) широко используют модель объекта в виде инерционного звена второго порядка с запаздыванием:
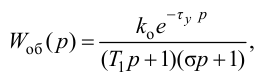
где 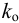
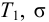
В этом случае величину условного запаздывания определяют по формуле
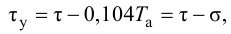
где 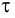
Если требуется заменить передаточную функцию объекта (4.15) на инерционное звено 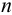
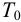
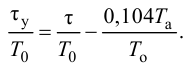
Откуда с учетом (4.11) и (4.12) получим
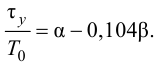
Поскольку малую постоянную времени о передаточной функции (4.15) объекта находят по формуле (4.19):
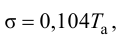
то ее относительное значение с учетом (4.12) примет вид
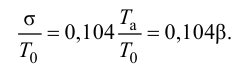
Обозначив сумму постоянных времени знаменателя передаточной функции (4.15) через 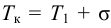
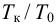
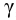
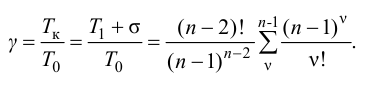
Так как большая постоянная времени передаточной функции объекта(4.15)
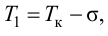
то ее относительное значение с учетом (4.20) и (4.21) примет следующий вид:
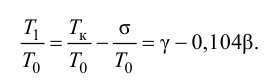
На основе полученных соотношений получена универсальная номограмма, позволяющая экспресс-методом определять численные значения параметров передаточных функций объектов регулирования в требуемом виде как на стадии проектирования, так и на основе экспериментальных переходных характеристик (рис. 4.2).
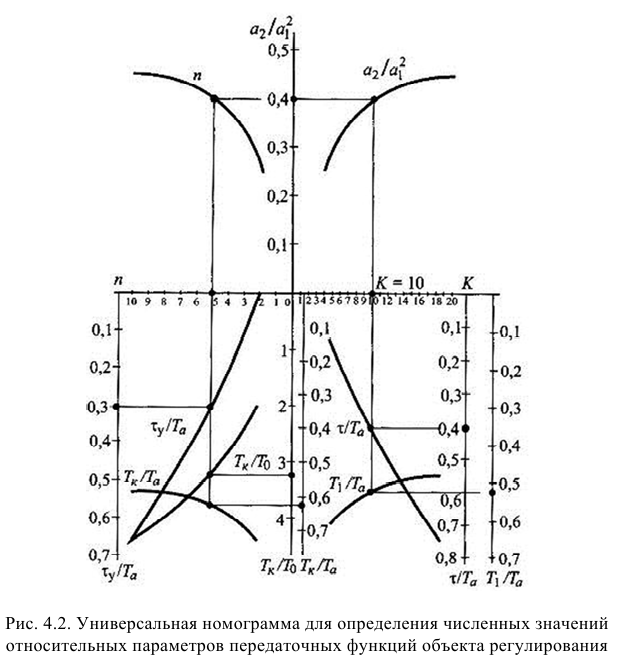
Пример использования номограммы. Если для пятой ступени пароперегревателя котла ПП-1600/250 для 70% нагрузки численные значения характерных параметров равны:
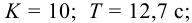
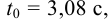
а требуется получить численные значения характерных параметров пароперегревателя в виде передаточных функций:
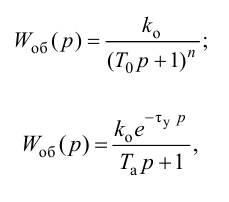
то в начале по номограмме находят отношение 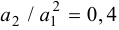
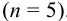
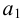
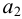
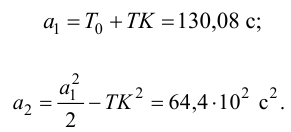
Затем определяют численное значение постоянной времени 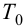
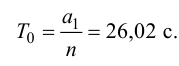
Полученным значениям 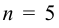
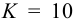
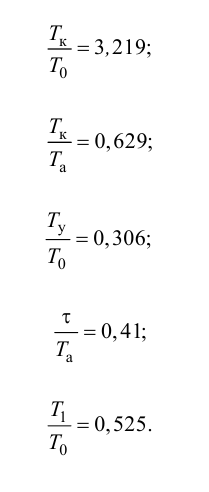
С учетом найденного значения 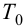
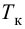
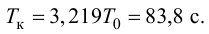
Далее из равенств (4.30) и (4.19) вначале находят время разгона 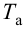
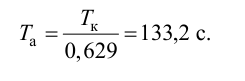
Потом определяют малую постоянную времени 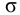
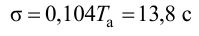
и с учетом (4.33) — большую постоянную времени 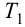
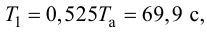
а также с учетом (4.31) — условное запаздывание 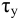
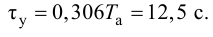
В результате искомая передаточная функция объекта (4.15) примет следующий вид:
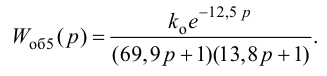
Для оценки точности аппроксимации коэффициентов передаточной функции (4.25) на основе номограммы с учетом (4.32) определим запаздывание 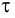
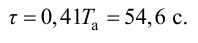
Так как численное значение запаздывания 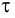
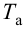
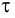
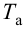
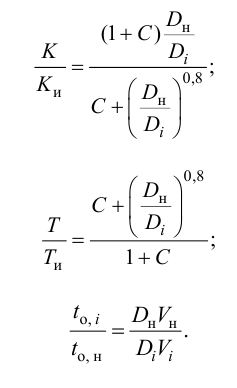
где «н» — соответствует номинальной нагрузке котла; 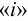
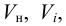
При этом вспомогательный коэффициент 
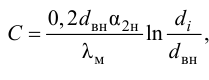
где 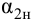
Постановка задачи оптимизации типовых линейных регуляторов
Типовые линейные регуляторы
Основным элементом системы автоматического регулирования является управляющее устройство, которое называется регулятором и выполняет основные функции управления путем выработки управляющего (регулирующего) воздействия в зависимости от ошибки регулирования.
Законы регулирования бывают линейные и нелинейные. Проще всего решать линейные уравнения. С нелинейными работать намного сложнее, причем многие типы уравнений аналитически решить пока не удается.
Рассмотрим основные линейные законы регулирования, которые реализованы в типовых линейных регуляторах.
Различают следующие типы регуляторов:
- пропорциональный (П-регулятор);
- интегральный (И-регулятор);
- пропорционально-интегральный (ПИ-регулятор);
- пропорционально-интегралыю-дифференциальиый (ПИД-регу-лятор);
- пропорционально-дифференциальный (ПД-регулятор).
К регулирующим устройствам относят также дифференциатор, но в промышленных условиях он обычно используется совместно с ПИ-регулятором для реализации ПИД-закона регулирования.
П-регулятор. П-регулятор перемещает регулирующий орган пропорционально отклонению регулируемой величины от заданного значения 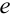
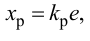
где 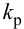
Регулятор, подчиняющийся этому закону, называют статическим с одним параметром динамической настройки (коэффициентом усиления), или пропорциональным П-регулятором.
Статическая характеристика П-регулятора представляет собой зависимость отклонения регулируемой величины 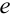
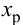
лятор называют статическим. При этом статическая ошибка регулятора находится по формуле
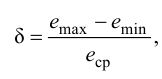
где 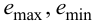
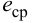
Передаточную функцию, комплексно-частотную характеристику (КЧХ) и переходную характеристику П-регулятора определяют по формулам:
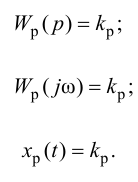
Пропорциональные регуляторы являются наиболее простыми и позволяют устойчиво регулировать промышленные объекты регулирования.
Недостатком таких регуляторов является остаточная неравномерность регулирования.
И-регулятор. И-регулятор перемещает регулирующий орган пропорционально интегралу от ошибки регулирования:
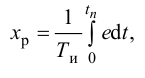
где 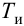
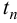
Этот регулятор называют астатическим с одним параметром динамической настройки 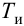
Статическая характеристика И-регулятора представляет прямую, параллельную оси абсцисс. Это следует из уравнения (5.4). Так как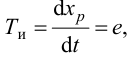
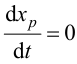
Передаточную функцию, КЧХ и переходную характеристику определяют по формулам:
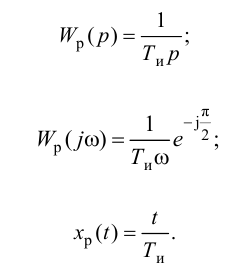
И-регуляторы могут устойчиво работать только с объектами, обладающими значительным самовыравниванием.
ПИ-регулятор перемещает регулирующий орган пропорционально сумме отклонения и интеграла отклонения регулируемой величины от заданного значения:
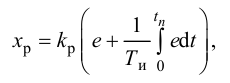
где 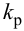
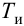
В динамическом отношении ПИ-регулятор подобен системе из двух параллельно включенных регуляторов: П-регулятора с коэффициентом передачи 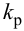
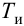
Передаточную функцию, КЧХ и переходную характеристику ПИ-регулятора (табл. 5.1) определяют по формулам:
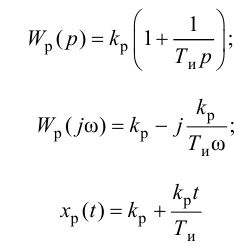
При беспредельном увеличении времени интегрирования ПИ-регулятор превращается в П-регулятор. Если 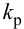
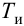
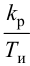
ПИ-регуляторы отличаются простотой конструкции и позволяют устойчиво и без остаточной неравномерности регулировать большое число промышленных объектов. Поэтому они широко распространены на практике.
ПИД-регуляторы перемещают регулирующий орган пропорционально отклонению, интегралу и скорости изменения отклонения регулируемой величины:
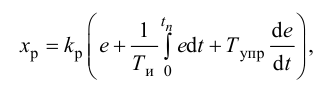
где 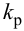
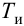
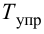
В динамическом отношении ПИД-регулятор подобен системе из трех параллельно включенных звеньев: пропорционального, интегрирующего и идеально дифференцирующего. При 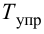
регулятор превращается в ПИ-регулятор; если, кроме того, 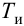
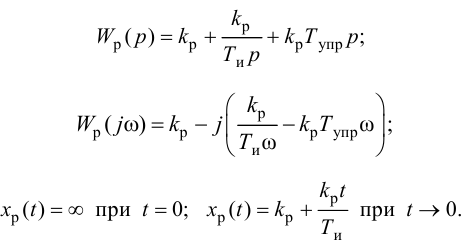
ПИД-регуляторы конструктивно сложнее ПП-регуляторов, однако они в ряде случаев позволяют улучшить качество регулирования технологических параметров. Они, как и ПИ-регуляторы, относятся к астатическим регуляторам и в настоящее время широко распространены.
ПД-регулятор. ПД-закон регулирования обычно применяют для коррекции динамических свойств автоматических систем регулирования. Идеальный пропорционально-дифференциальный регулятор имеет передаточную функцию
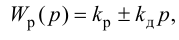
где 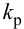
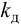
Реальный (инерционный) пропорционально-дифференциальный регулятор имеет передаточную функцию вида
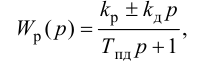
где
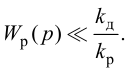
Сказанное справедливо и для реального ПД-регулятора с той разницей, что влияние инерционного звена 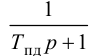
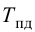
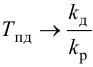
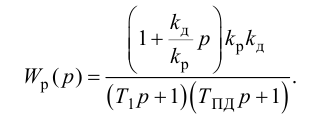
Тогда даже при 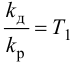
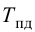
Под параметрической оптимизацией типовых регуляторов понимают такое определение параметров их динамических настроек, которое обеспечивает выполнение принятых критериев оптимальности для данных возмущений.

Синтез оптимальных алгоритмов функционирования и параметрическая оптимизация одноконтурных систем автоматического регулирования для объектов с запаздыванием
Передаточную функцию объекта по каналу регулирующего воздействия представим в виде
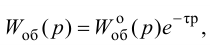
где 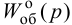
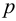
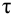
Требуемую переходную характеристику одноконтурной системы по задающему воздействию представим в виде передаточной функции колебательного звена с запаздыванием:
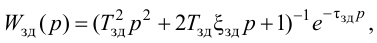
где 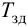
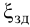
При 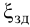
и минимальное перерегулирование. При 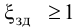
Выражение оптимальной передаточной функции регулятора с учетом (5.13) и (5.14) примет вид
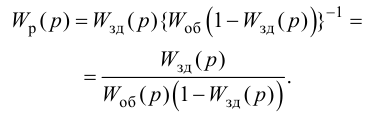
Разность 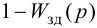
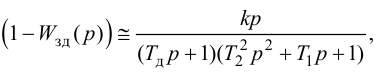
желаемые значения параметров которого выбирают с учетом (5.14) из условия равенства площадей под ломаной кривой, соответствующей левой части равенства (5.16), и плавной кривой, соответствующей правой части равенства (5.16):
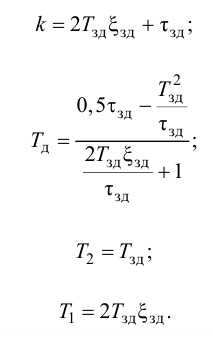
С учетом (5.16) оптимальную передаточную функцию регулятора (5.15) представим в виде
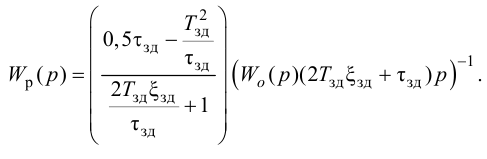
Полученная таким образом передаточная функция регулятора 
В табл. 5.3 приведены передаточные функции типовых оптимальных регуляторов, а также соответствующие каждому алгоритму регулирования частные случаи передаточной функции объекта (5.13) и формулы для определения параметров оптимальной динамической настройки, удовлетворяющие условию (5.14) метода полной компенсации (МПК) большей постоянной времени объекта (п. 1-6). Здесь же даны оптимальные значения параметров динамической настройки типовых регуляторов для внутренних возмущений (п. 7-9), где приняты следующие обозначения в критериях оптимальности: 
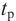
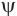
МЧК — метод частичной компенсации для объектов без запаздывания;
ММЧК — модифицированный метод частичной компенсации для объектов с запаздыванием;
МЧКО — метод частичной компенсации с ограничением максимальной величины регулирующего воздействия (табл. 5.3).
Если желаемая передаточная функция системы по задающему воздействию имеет вид инерционного звена с запаздыванием
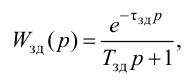
то передаточная функция оптимального регулятора примет вид
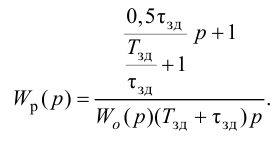
Подставив в (5.20) конкретные передаточные функции части объекта без запаздывания 
Отметим некоторые особенности рассмотренных методов. Так как задача параметрической оптимизации САР по задающему воздействию решена в общем виде, то некоторые формулы для расчета настройки типовых регуляторов, приведенные в табл. 5.3, совпадают с формулами других методов оптимизации либо получены другими способами для конкретных передаточных функций объекта.
Сравним приведенные выше методы с данными, приведенными в работах В. Я. Ротача, где оптимизация типовых регуляторов осуществлена на основе минимизации дисперсии погрешности регулирования без ограничения запаса устойчивости системы. Видно, что для типовых ПИД-, ПИ- и И-алгоритмов регулирования (см. табл. 5.3) временные параметры динамической настройки регуляторов совпадают, а коэффициенты передачи регуляторов в общем случае в два раза меньше. Этот факт позволяет установить причину появления слабо затухающих колебаний переходных процессов в системе, интенсивность затухания которых оказывается, как правило, из-за увеличенного значения коэффициента передачи регулятора, явно недостаточной для эксплуатации САР в реальных условиях.
Синтез оптимальных параметров динамической настройки ПИ-регуляторов при внутренних возмущениях
При определении оптимальных параметров динамической настройки регулятора из условия минимума среднеквадратичной ошибки регулирования дополнительно к интегральному критерию оптимальности вводят условие обеспечения заданной степени затухания переходных процессов. Это достигается двумя наиболее распространенными способами:
1) заданием в плоскости комплексной частотной характеристики разомкнутой системы регулирования области, включающей в себя «опасную» точку 
2)заданием в плоскости корней характеристического уравнения системы области, в пределах которой должны находиться эти корни.
Использование первого метода требует определения комплексной частотной характеристики объекта, второго — предварительного вычисления расширенных частотных характеристик объекта и регулятора. Причем применение обоих способов сопряжено со значительными трудозатратами на выполнение расчетов, а для вычисления прямых показателей качества требуется непосредственное построение переходных процессов системы регулирования при расчетных значениях настройки регулятора.
Можно существенно упростить алгоритм определения настройки регулятора и прямых показателей качества переходных процессов системы регулирования, положив в основу второй способ введения ограничения в критерий оптимальности.
Пусть 
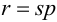
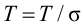
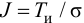
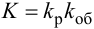
Передаточная функция ПИ-регулятора имеет вид.
Передаточная функция регулятора в относительном времени соответствует
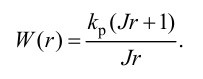
Передаточная функция объекта в относительном времени в виде инерционного звена второго порядка соответствует
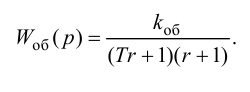
Передаточная функция замкнутой системы при обработке скачкообразного внутреннего возмущающего воздействия с учетом (5.21) и (5.22) примет вид:
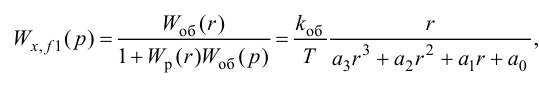
где
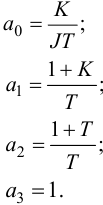
Приведем передаточную функцию (5.23) к нормированной форме Вышнеградского изменением масштаба 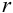
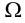
Заменив в передаточной функции аргумент 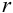
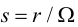
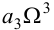
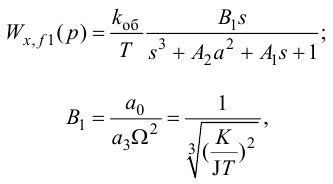
где
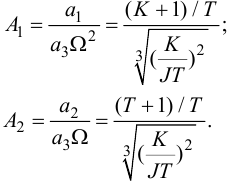
При этом новому оператору 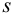
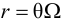
После несложных преобразований представим относительные параметры динамической настройки ПИ-регулятора в виде функции от относительной постоянной времени 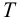
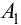
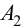
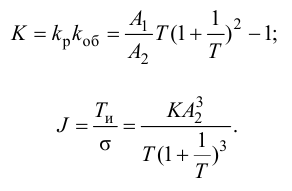
Численные значения коэффициентов Вышнеградского 
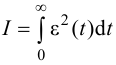
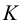
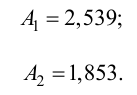
Формулы (5.28) и (5.29) с учетом (5.30) и (5.31) примут следующий вид:
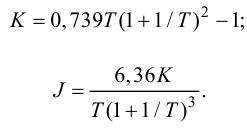
Данный метод определения оптимальной настройки ПИ-регуля-тора называется методом частичной компенсации (МЧК) большей постоянной времени объекта регулирования.
Из уравнения (5.24) и (5.27) находим, что
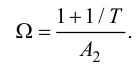
Тогда с учетом (5.33) из (5.27) получаем выражение для коэффициента 
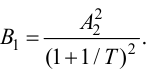
Передаточную функцию замкнутой системы (5.26) с учетом (5.30), (5.31) и (5.34) можно записать следующим образом:
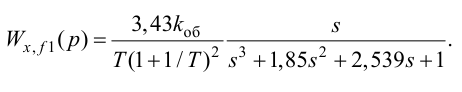
Переходная функция системы (5.36) в относительном времени 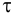
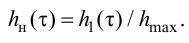
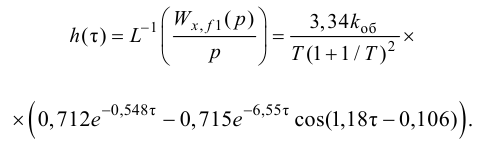
Для облегчения расчетов переходных процессов по формуле (5.37) на рис. 5.1 и 5.2 приведены графики зависимостей
Переходный процесс в САР при отработке внутреннего возмущения (см. рис. 5.1 и 5.2) можно определить по формуле
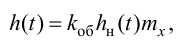
где 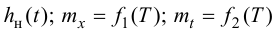
где 
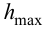
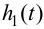
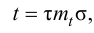
где 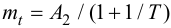
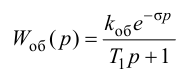
оптимальные параметры динамической настройки ПИ-регуляторов можно рассчитать на основе расширенных частотных характеристик (РАФХ) объекта и регулятора с использованием формул модифицированного метода частичной компенсации (ММЧК).
При этом параметрические уравнения линии равного затухания в области параметров динамической настройки ПИ-регулятора определяют по следующим формулам:
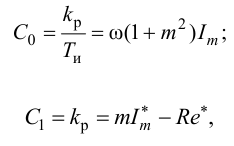
где 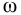
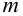
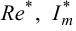
Взяв передаточную функцию, обратную (5.40), и заменив оператор 
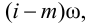
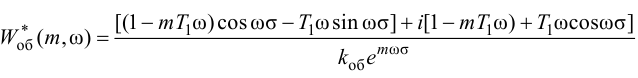
откуда получаем
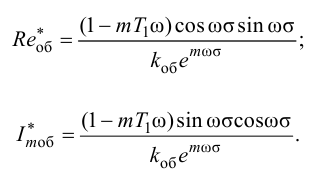
Подставим (5.42) в (5.41) и перейдя к относительным величинам, получим уравнения, определяющие линии равного затухания для АСР передаточной функцией объекта (5.39):
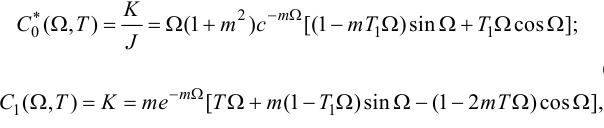
где
Изменяя относительную частоту 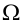
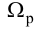
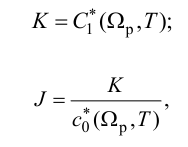
при выполнении условий критерия оптимальности
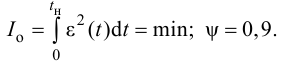
Для облегчения расчетов относительных параметров динамической настройки ПИ-регуляторов по формулам (5.44) при выполнении условия (5.45) можно использовать аналитические зависимости параметров настройки как функции относительной постоянной времени объекта 
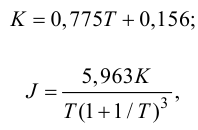
где
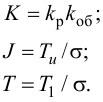
Для определения оптимальных значений параметров динамической настройки ПИ-регуляторов можно воспользоваться графиками, приведенными на рис. 5.3 и рассчитанными по формулам (5.44).
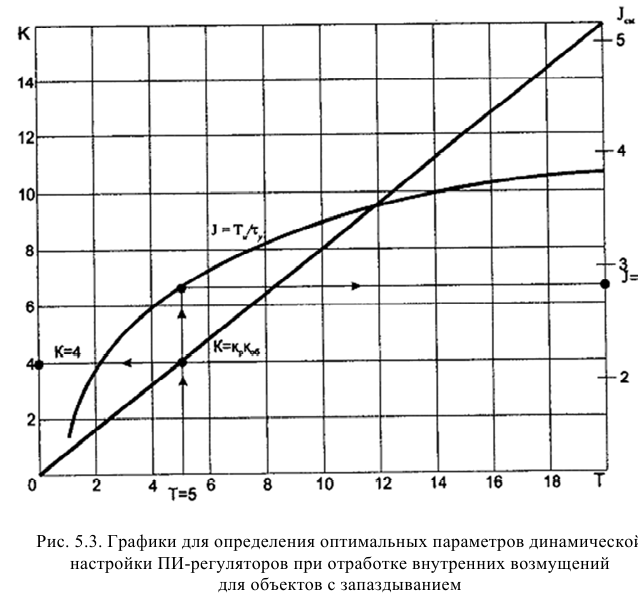
Для построения переходных процессов в САР и ПИ-регуляторами параметры, настройки которых рассчитаны по данной методике, и определения прямых показателей качества при отработке внутренних возмущающих воздействий на рис. 5.4 приведены графики нормированных переходных процессов 
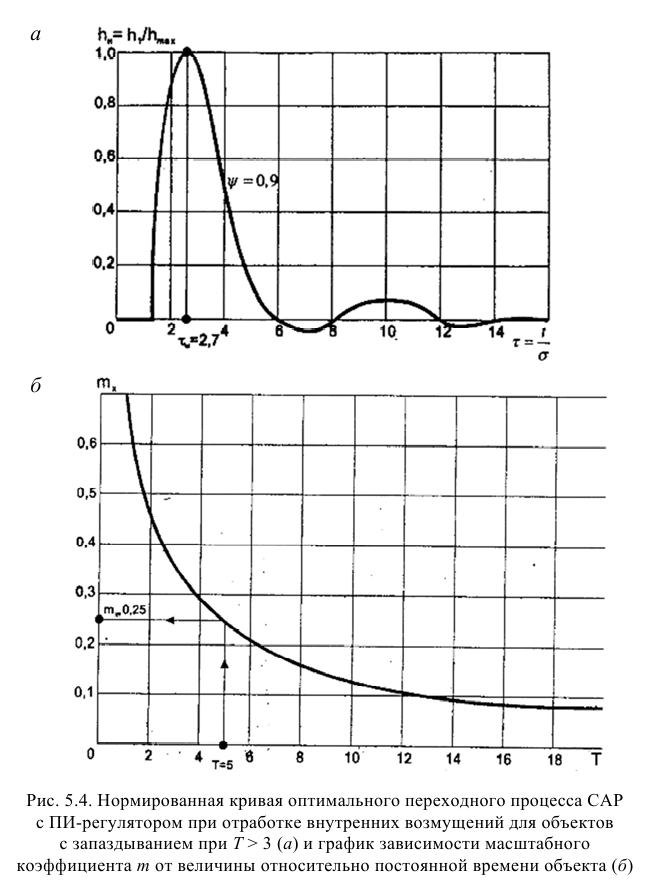
Они позволяют получить искомый переходной процесс САР для конкретного объекта регулирования, представленного относительной постоянной времени 
Нормированной кривой (рис. 5.4, а) можно пользоваться для объектов с 
Графики нормированных переходных процессов САР с ПИ-регуляторами и объектами с относительными постоянными времени 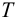
Дополнительная теория из учебников:
- Сущность проблемы автоматического управления
- Фундаментальные принципы управления
- Основные виды алгоритмов функционирования
- Об основных законах управления
- Уравнения динамики и статики. Линеаризация
- Основные свойства преобразования Лапласа
- Формы записи линейных дифференциальных уравнений. Передаточные функции
- Частотные характеристики
- Временные характеристики
- Элементарные звенья и их характеристики
Параметрическая оптимизация дискретного ПИД-регулятора
Обычно к параметрически оптимизируемым относят широко используемые П-, ПИ-, или ПИД-регуляторы, дифференциалыю-интег-ральные уравнения которых можно преобразовать с помощью дискретизации. Такой подход позволяет использовать накопленный опыт работы с аналоговыми регуляторами и в принципе применять уже хорошо известные правила настройки динамических параметров этих регуляторов без переподготовки и обслуживающего персонала.
Идеализированное уравнение ПИД-регулятора имеет вид
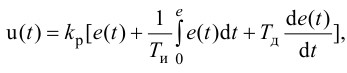
где 
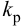
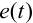
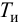
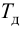
Для малых тактов квантования постоянных времени 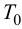
При использовании метода прямоугольников получаем
где 
Таким образом, мы получили не рекуррентный алгоритм управления. В нем для формирования суммы необходимо помнить все предыдущие значения сигнала ошибки 
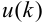
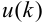
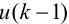
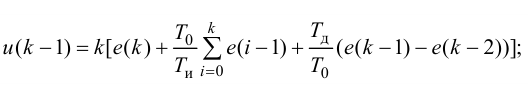
В результате получим следующую разность
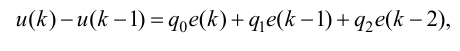
где
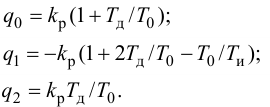
Теперь вычисляют только текущее приращение управляющей переменной 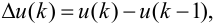
Следует отметить, что после небольшой модификации способа интегрирования в уравнении (5.50) под знаком суммы используют значения 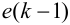
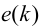
Если для аппроксимации интеграла использовать метод трапеций, то на основании уравнения (5.48) будет получено следующее соотношение:
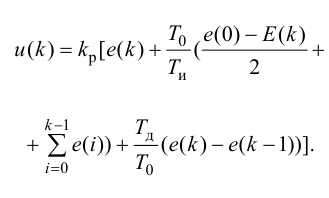
Вычитая из него соответствующее уравнение для 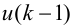
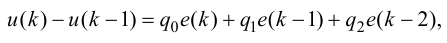
где
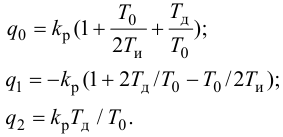
Для малых тактов квантования параметры 
При больших тактах квантования способы дискретной аппроксимации непрерывных регуляторов становятся несправедливыми.
Рассмотрим простой контур управления, изображенный па рис. 5.6. Дискретная передаточная функция объекта управления с экстрапо-лятором нулевого порядка имеет вид
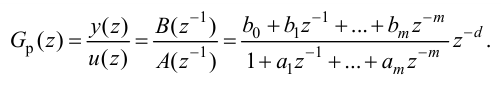
Обобщенная дискретная передаточная функция линейного регулятора записывается как
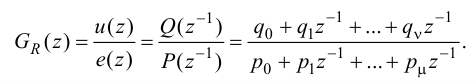
Этот алгоритм может быть реализован, если 
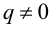
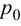
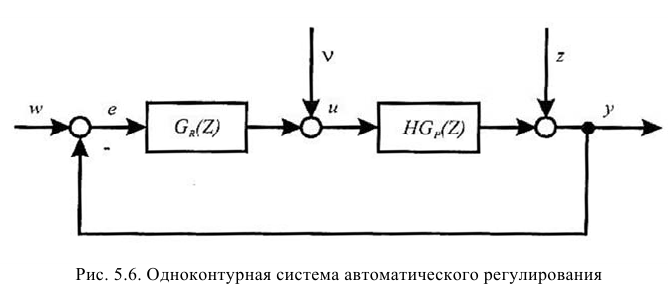
В структурно оптимизируемых регуляторах порядки числителя и знаменателя передаточной функции 
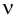
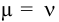
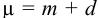
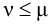
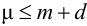
При выборе структуры параметрически оптимизируемых регуляторов обычно необходимо гарантировать, чтобы изменения задающей переменной и возмущений не приводили к появлению статической ошибки по сигналу 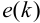
Следовательно, простейшие алгоритмы управления 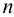
При 
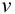
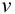
Для получения хорошего качества процессов управления параметры 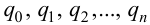
а) на основе метода, использующего модель объекта управления, в результате минимизации критерия качества с использованием параметрической оптимизации, причем аналитическое решение возможно лишь для объектов и регуляторов очень низкого порядка, в остальных случаях следует применять численные методы;
б) с использованием алгоритмов параметрической настройки, позволяющих получить параметры регулятора, близкие к оптимальным для некоторого критерия. Обычно для этого необходимо оценивать либо параметры переходного процесса в системе при ступенчатом задающем воздействии, либо критическое значение коэффициента усиления и период колебаний на границе устойчивости системы;
в) последовательного увеличения значений параметров от их малых начальных значений до тех пор, пока переходный процесс в замкнутой системе не приобретет значительной колебательности.
После этого следует понемногу уменьшать значения параметров (метод проб и ошибок).
Если к системе управления не предъявляют каких-либо специфических требований и ее переходный процесс отличается простотой и малым временем установления, то для оптимизации параметров регулятора достаточно использовать методы, упомянутые в пп. бив. Если требования строги или переходный процесс оказывается сложным, медленным или существенно изменяющимся, то следует применять метод, упомянутый в п. а. Этот метод также пригоден для автоматизации проектирования регуляторов.
Задав 
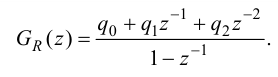
Запишем соотношение в соответствии с уравнением (5.58)
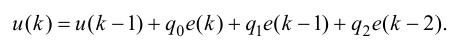
Рассматривая единичное ступенчатое изменение сигнала ошибки
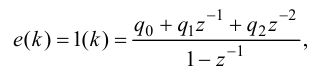
сформируем систему уравнений для последовательных значений выходного сигнала регулятора 
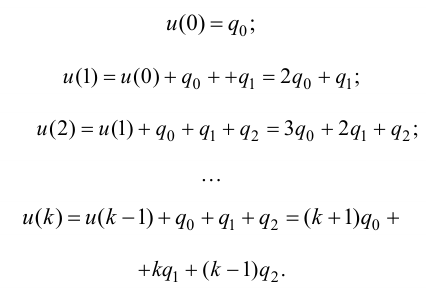
В случае, когда 
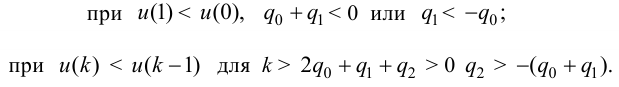
Для положительного коэффициента передачи регулятора выполняется условие 
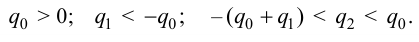
Реакция регулятора на единичное ступенчатое входное воздействие приведена на рис. 5.7. Как видно из рис. 5.7, начальное значение управляющей переменной 
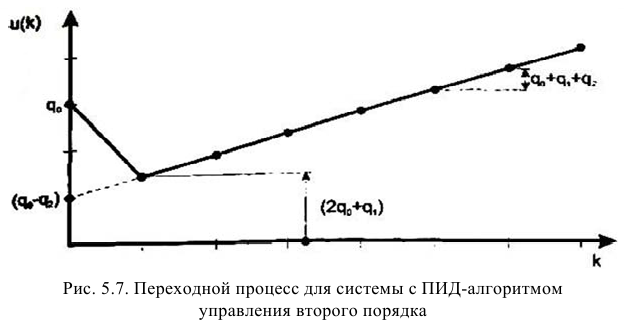
Определим следующие коэффициенты, характеризующие свойства регулятора (рис. 5.8):
Коэффициенты (5.64) при малых значениях такта квантования 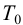
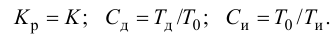
Если рассмотренные выше коэффициенты подставить в выражение (5.59), то дискретная передаточная функция регулятора примет вид
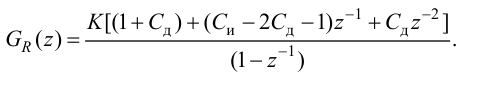
Следует отметить, что рассмотренный выше алгоритм управления второго порядка является аналогом непрерывного ПИД-регу-лятора с положительными параметрами только в том случае, если выполняются условия (5.64) и (5.65).
На рис. 5.7 показана реакция такого дискретного ПИД-регуля-тора на единичный ступенчатый скачок.
На основе формул для настройки непрерывных регуляторов, приведенных в табл. 5.5, могут быть получены параметры оптимальной динамической настройки дискретных регуляторов. Например, для дискретной передаточной функции ПИД-регулятора, представленной в виде (5.66), коэффициенты передачи, дифференцирования и интегрирования дискретного ПИД-регулятора определяют по формулам:
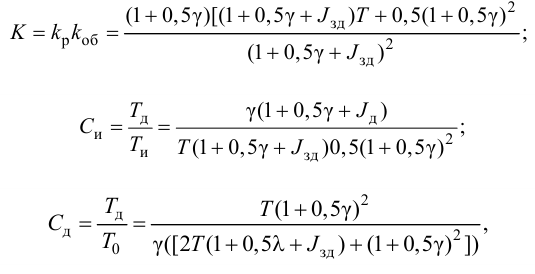
где 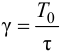
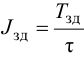
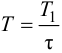

Параметры дискретного ПИД-регулятора получены из соответствующих соотношений для непрерывных регуляторов путем замены в них чистого запаздывания величиной 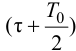
Для того, чтобы эффект квантования по времени мало сказывался на динамику системы цифрового регулирования, рекомендуется выбирать период квантования из соотношения
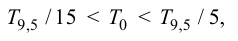
где 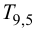
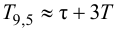
Другой подход к выбору величины периода квантования основан на рекомендациях американских ученых Циглера и Никольса, согласно которым 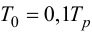
В реальных условиях при управлении инерционными процессами значение 
С целью упрощения процедуры настройки цифрового ПИД-регулятора рекомендуется (согласно Циглеру и Никольсу) выбирать следующие значения отношений:
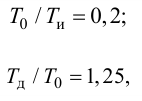
при
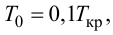
где 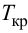
Чтобы получить приближенно оптимальный набор параметров непрерывных ПИД-регуляторов, часто применяют так называемые «правила настройки». Обычно эти правила предназначены для низкочастотных объектов регулирования.
Опубликовано большое количество модификаций дискретных алгоритмов управления, основанных на дискретизации дифференциальных уравнений непрерывных ПИД-регуляторов. Некоторые из них рассмотрены ниже.
Для уменьшения больших изменений управляющей переменной при резких изменениях задающего сигнала задающее воздействие исключают из дифференцирующего члена алгоритма функционирования ПИД-регулятора:
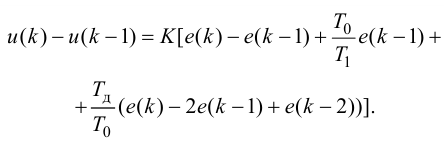
При этом используется модифицированный алгоритм
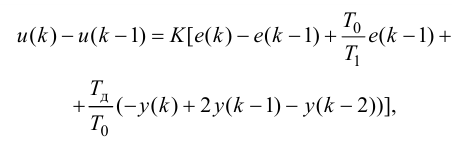
где
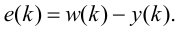
Дополнительного уменьшения амплитуды управляющей переменной добиваются, оставляя значения задающего сигнала только в интегрирующем члене алгоритма:
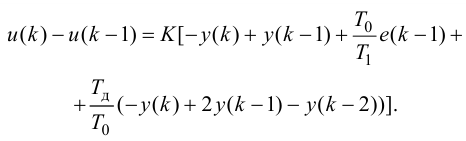
В последнем алгоритме предпочтительнее использовать сигнал 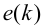
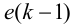
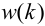
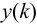
Другие модификации алгоритмов управления состоят в различных способах реализации дифференцирующей части. Часто регулируемая переменная содержит относительно высокочастотный шум, который не измеряется. Это приводит к нежелательным существенным колебаниям управляющей координаты, если дифференцирующая часть алгоритма сформирована с использованием первой разности в нерекуррентной форме
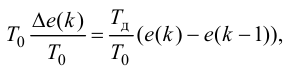
или рекуррентной форме (5.69)
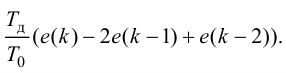
Введение дифференцирующего члена в алгоритм управления часто может быть необходимым для улучшения качества процессов управления при наличии среднечастотных шумов не слишком большого уровня, поскольку в этом случае происходит приближенное сокращение полюсов объекта, что приводит к расширению областей устойчивости и возможности увеличения коэффициента передачи. Следовательно, при введении дифференцирующего члена в алгоритм управления следует, учитывая вышесказанное, выбирать его параметры для обеспечения допустимого компромисса.
Одна из возможностей состоит в том, чтобы выбирать отношение 
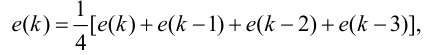
после чего все аппроксимации первой производной усредняются по отношению к 
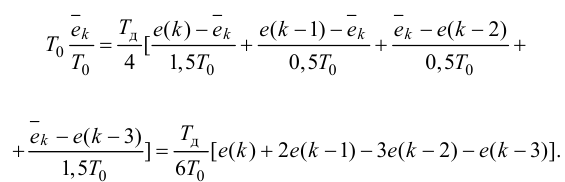
Для рекуррентной формы имеем
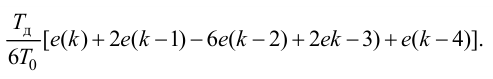
Еще один подход, применимый лишь при выборе малых тактов квантования в системе, состоит в использовании такого дифференцирующего члена, как в непрерывной передаточной функции:
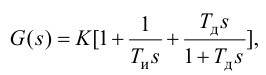
в применении соотношения
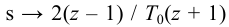
для аппроксимации непрерывных зависимостей. Из приведенного непрерывного в результате такой подстановки получим следующий дискретный алгоритм управления:
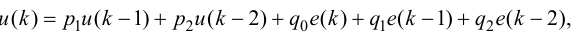
параметрами которого являются:
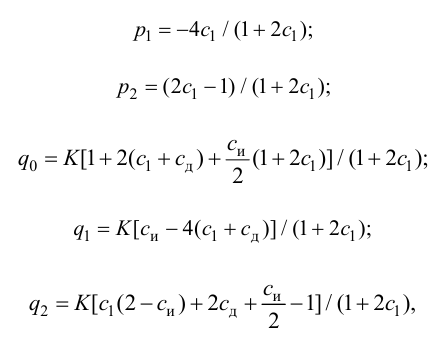
где
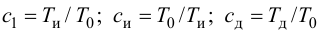
для объектов, динамика которых может быть аппроксимирована передаточной функцией вида
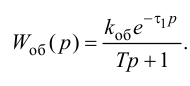
Однако с помощью этих соотношений для непрерывных регуляторов можно получить параметры дискретных регуляторов, если вместо чистого запаздывания 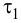
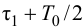
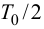
Правила настройки параметров, основанные на определении характеристик переходного процесса для модифицированных алгоритмов управления, приведены в табл.5.5.
Алгоритм управления:
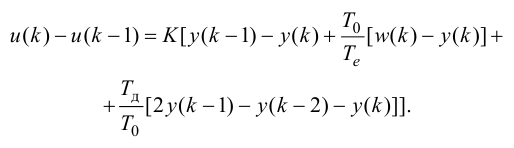
Динамическая оптимизация одноконтурных систем автоматического регулирования
Метод полной компенсации в частном виде
Метод полной компенсации в частном виде — это один из методов расчета параметров оптимальной динамической настройки ПИ-регулятора для отработки скачка задания или крайнего внешнего возмущения.
Метод применяют в одноконтурной системе автоматического регулирования для объекта в виде инерционного звена второго порядка.
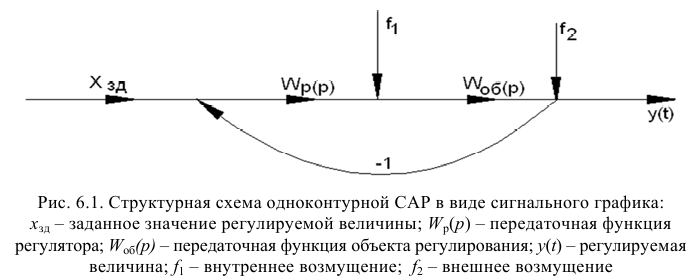
Дииамика объекта регулирования представлена в виде передаточной функции инерционного звена второго порядка без запаздывания:
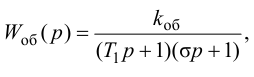
где 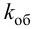
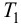
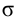
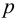
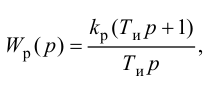
где 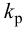
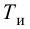
Скачок наиболее опасного крайнего внешнего возмущения 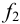
Критерий оптимальности: считаются оптимальными такие параметры динамической настройки ПИ-регулятора, которые в замкнутой САР при отработке скачка задания обеспечат такую же динамику, как у колебательного звена с коэффициентом демпфирования 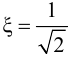
При этом система регулирования будет оптимальна по быстродействию в отработке скачка задания, а переходный процесс будет содержать одно колебание с максимальной величиной перерегулирования 4,3 % от скачка задания. МПКЧВ так называют, потому что происходит компенсация большей постоянной времени 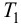
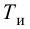
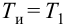
Оптимальными параметрами динамической настройки ПИ-регулятора будем считать такие численные значения 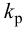
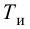
Передаточная функция замкнутой САР по задающему воздействию примет вид
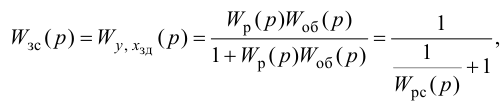
где передаточная функция разомкнутой системы
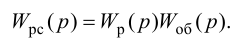
Передаточная функция разомкнутой САР примет вид
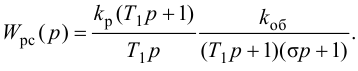
Подставим (6.5) в (6.3):
Так как в качестве критерия оптимальности взято колебательное звено с коэффициентом передачи 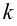
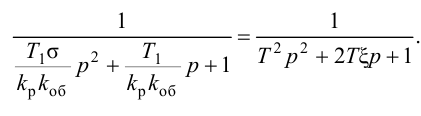
Чтобы левая и правая части равенства (6.7) соответствовали друг другу, составим систему уравнений:
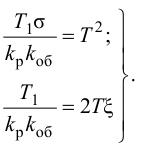
Возводим в квадрат обе части последнего равенства:
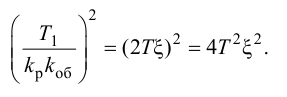
Из уравнения (6.9) находим 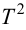
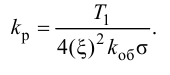
Так как 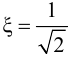
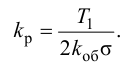
Если отработка задания не допускает перерегулирования, то коэффициент демпфирования принимается 
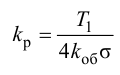
Для объектов с запаздыванием и передаточной функцией вида
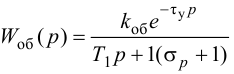
применимы формулы МПКЧВ для объектов без запаздывания. В этом случае 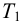
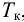
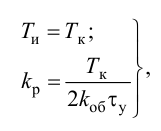
где
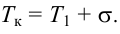
Графоаналитический метод полной компенсации в общем виде
Метод полной компенсации в общем виде (МПКОВ) — это один из методов оптимальной настройки САР для оптимальной отработки крайнего внешнего возмущения. Указанный метод позволяет выбрать тип регулятора для конкретного объекта регулирования, а затем для выбранного типа регулятора вывести формулы расчета параметров оптимальной динамической настройки в соответствии с принятым критерием качества (рис. 6.2).
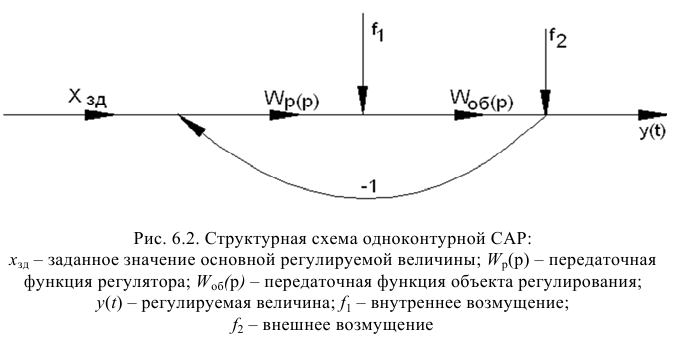
МПКОВ так называют, потому что динамика объекта регулирования представлена в общем виде:
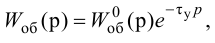
где 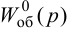
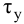
Критерий оптимальности:
выбираем такой тип регулятора и параметры его динамической настройки, которые при отработке скачка задания обеспечивают переходной процесс, соответствующий последовательно соединенным звеньям условного запаздывания и инерционного звена первого порядка. При этом время разгона 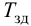
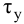
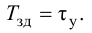
Выбранному критерию оптимальности будет соответствовать передаточная функция:
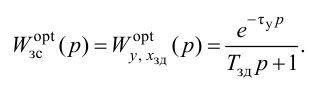
Принятый критерий оптимальности в виде последовательно соединенных звеньев чистого запаздывания и инерционного звена первого порядка графически можно представить в виде кривой 1 на рис. 6.3.
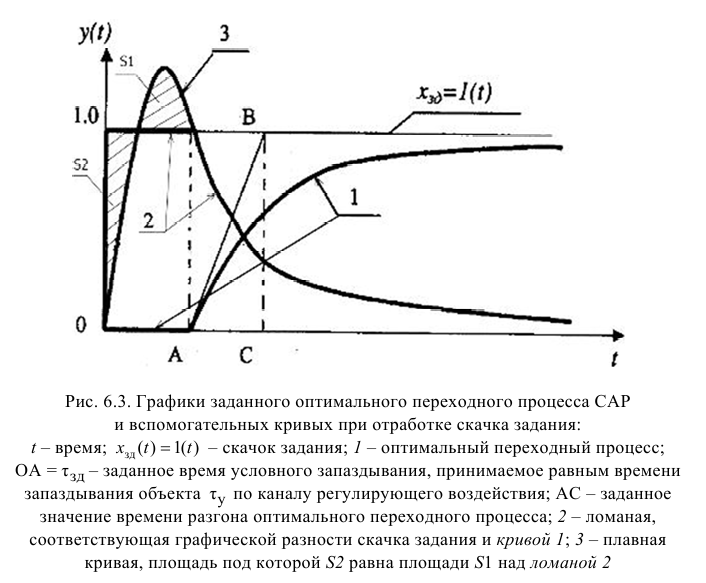
Запишем передаточную функцию замкнутой САР по задающему воздействию
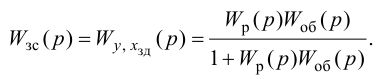
Меняя тип регулятора и его настройки в формуле (6.17), можно получить любые переходные процессы замкнутой САР, а нужен один переходной процесс, соответствующий выбранному критерию оптимальности
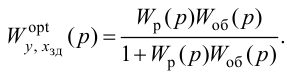
Из равенства (6.18) находим передаточную функцию регулятора соответствующего вида и критерия оптимальности (6.16)
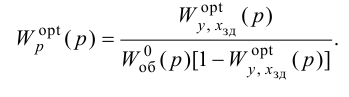
Разность 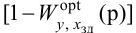
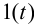
Кривую 2 можно представить в виде последовательно соединенных реального дифференцирующего звена и инерционного звена первого порядка:
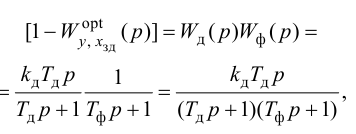
где 
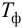
При этом передаточной функции (6.20) будет соответствовать кривая 3 на рис. 6.3, а для того, чтобы выполнялось равенство (6.20), необходимо, чтобы площади 
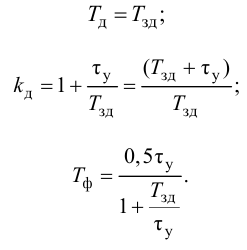
Подставив равенства (6.21), (6.22), (6.23) в передаточную функцию правой части равенства (6.20), получим
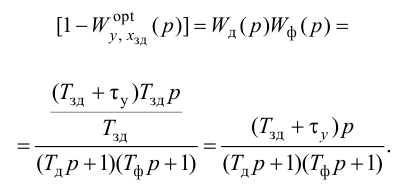
Подставив в передаточную функцию (6.19) передаточные функции объекта (6.14), оптимальной замкнутой САР (6.16), разности (6.24) с учетом условий (6.21) и (6.22), получим искомую передаточную функцию оптимального регулятора:
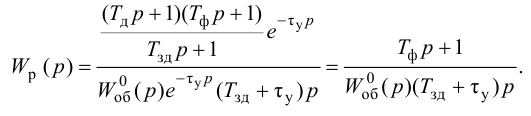
Если в передаточную функцию (6.25) подставить ту часть передаточной функции конкретного объекта, которая не содержит запаздывания, то формула (6.25) позволит установить тип регулятора, а затем рассчитать параметры его оптимальной динамической настройки, чтобы удовлетворить условие критерия оптимальности (6.16).
Пример 6.1.
На рис. 6.4 представлен график экспериментальной переходной характеристики объекта регулирования с запаздыванием по каналу регулирующего воздействия.
Передаточную функцию объекта регулирования представим в виде
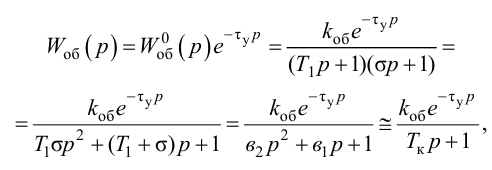
где 
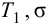
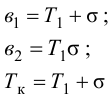
эквивалентная постоянная времени.
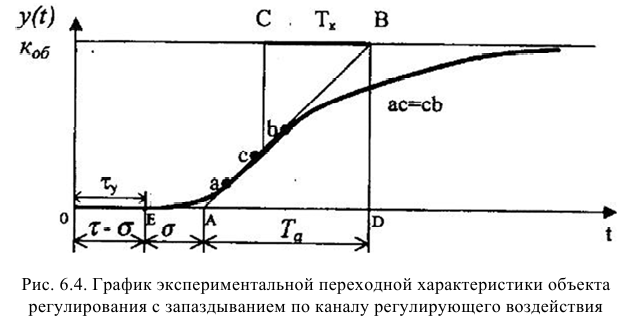
Требуется определить передаточную функцию оптимального регулятора на основе передаточной функции (6.25).
Алгоритм определения численных значений параметров передаточных функций объекта и оптимального регулятора:
- Проводим касательную
к переходной характеристике объекта (рис. 6.4) таким образом, чтобы как можно больше точек прямой
и переходной характеристики объекта совпали (отрезок
).
- Находим середину отрезка
(точка
).
- Восстанавливаем перпендикуляр с
.
- Полученный отрезок
.
- Опускаем перпендикуляр
на ось времени.
- Полученный отрезок
обозначим через
.
- Находим численное значение малой постоянной времени объекта
по формуле
и откладываем влево от точки
по оси времени так, чтобы
.
- С учетом найденного значения
определяем численное значение большей постоянной времени объекта
.
- Определяем численное значение условного запаздывания объекта
, где
— чистое запаздывание.
Определим структуру оптимального регулятора с использованием передаточной функции объекта в виде
где
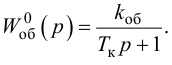
Подставив передаточную функцию (6.28) в передаточную функцию оптимального регулятора (6.25), построенного по методу полной компенсации в общем виде, получим:
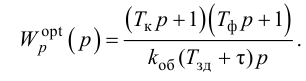
Умножив числитель и знаменатель передаточной функции (6.29) на 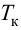
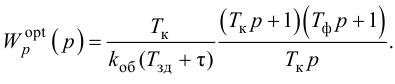
Из общего вида передаточной функции (6.30) следует, что для данного объекта оптимальным типовым регулятором является ПИД-регулятор с передаточной функцией вида:
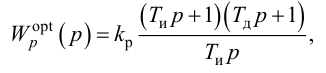
параметры дииамичеекои наетроики которого путем сравнения соответствующих сомножителей уравнений (6.30) и (6.31) с учетом того, что
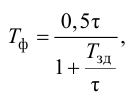
можно определить по следующим формулам:
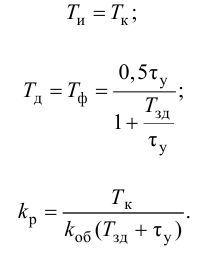
где 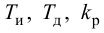
Для получения максимального быстродействия в системе регулирования нужно принять 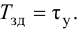
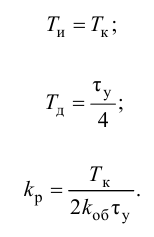
При этих настройках полное время отработки скачка задания в САР с ПИД-регулятором не превышает 
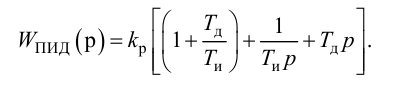
При малом значении времени дифференцирования и большой величине времени интегрирования 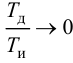
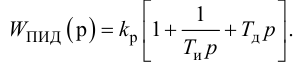
В этом случае в качестве критерия оптимальности при отработке скачка задания можно принять колебательное звено с коэффициентом демпфирования, равным 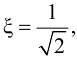
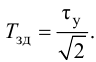
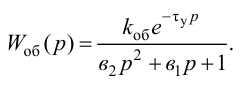
В этом случае параметры оптимальной динамической настройки ПИД-регулятора определяют по следующим формулам:
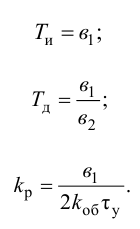
Эти настройки регулятора обеспечивают минимальное время отработки скачка задания. При этом величина максимального перерегулирования не превышает 5 %.
Дополнительная теория из учебников:
- Понятие устойчивости
- Общая постановка задачи устойчивости по А. М. Ляпунову
- Теоремы к. М. Ляпунова об устойчивости движения по первому приближению
- Условия устойчивости линейных систем автоматического управления
- Алгебраические критерии устойчивости
- Анализ устойчивости по логарифмическим частотным характеристикам
- Устойчивость нестационарных систем
- Методы оценки качества регулирования линейных систем
- Оценка качества переходного процесса при воздействии ступенчатой функции
Аналитический метод полной компенсации в общем виде
Динамика объекта регулирования задана в виде передаточной функции
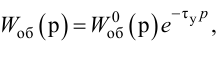
где 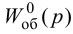
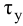
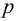
Передаточная функция оптимального регулятора имеет вид
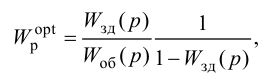
где 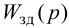
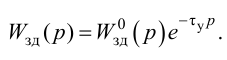
Передаточную функцию условного запаздывания представим в следующем виде:
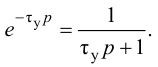
Подставив в передаточную функцию оптимального регулятора (6.46) передаточные функции (6.45), (6.47) и (6.48), получим:
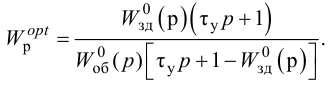
Пример 6.2.
Передаточная функция объекта регулирования задана в виде инерционного звена первого порядка с условным запаздыванием:
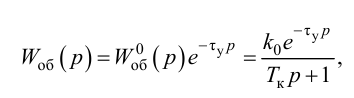
где
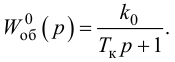
Требуется определить оптимальную передаточную функцию регулятора на основе передаточной функции (6.49).
Заданная передаточная функция системы согласно (6.47) примет следующий вид:
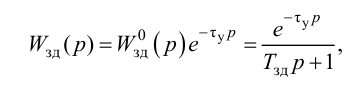
где
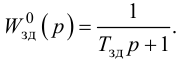
Подставив в передаточную функцию оптимального регулятора (6.49) передаточные функции (6.51) и (6.53), получим
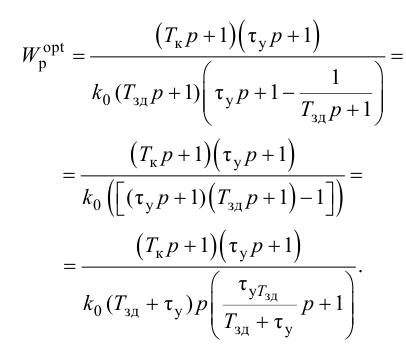
Получаем передаточную функцию реального ПИД-регулятора с одним параметром динамической настройки 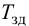
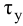
Пример 6.3.
Передаточная функция объекта регулирования задана в виде инерционного звена второго порядка с запаздыванием:
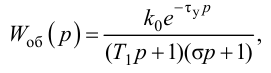
где 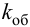
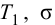
В этом случае заданная передаточная функция системы с учетом структуры (6.55) примет следующий вид:
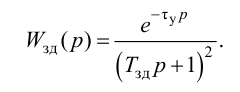
Подставив передаточные функции (6.55) и (6.56) в передаточную функцию оптимального регулятора (6.49), получим:
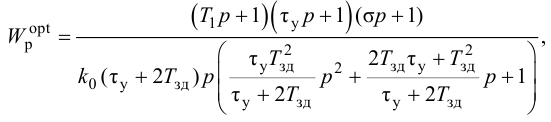
то есть передаточную функцию реального ПИДД-регулятора с инерционностью второго порядка.
Параметрическая оптимизация типовых двухконтурных систем автоматического регулирования
Параметрическая оптимизация типовых каскадных систем автоматического регулирования теплоэнергетических процессов
Рассмотрим каскадную систему автоматического регулирования (КСАР) с корректирующим и стабилизирующим регуляторами (рис. 7.1).

Методика определения параметров настройки регуляторов каскадной системы автоматического регулирования основана на возможности расчета одного контура (стабилизирующего или внутреннего) независимо от другого (корректирующего или внешнего). Для этого параметрическую оптимизацию стабилизирующего регулятора произведем с использованием метода частичной компенсации, а корректирующего регулятора — с использованием метода полной компенсации в общем виде.
Метод частичной компенсации предназначен для оптимальной отработки внутреннего возмущения с использованием ПИ-регулятора:
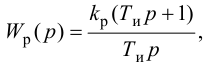
где 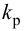
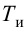
Передаточная функция опережающего участка объекта регулирования задана в виде инерционного звена второго порядка:
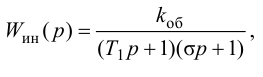
где 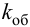
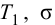
Критерий оптимальности — минимум интеграла квадрата ошибки регулирования при заданной степени затухания 
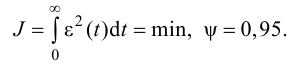
Определяем параметры динамической настройки стабилизирующего ПИ-регулятора с учетом формул (5.32) и (5.33):
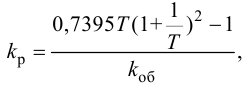
где 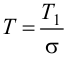
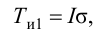
где 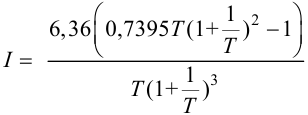
При этом передаточная функция корректирующего регулятора, параметры динамической настройки которого позволяют оптимально отрабатывать крайнее внешнее возмущение, примет вид, согласно передаточной функции (6.25):
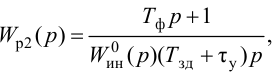
где 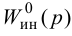
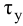
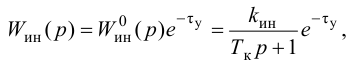
причем 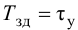
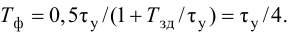
В результате чего передаточная функция корректирующего регулятора примет вид ПИД-регулятора:
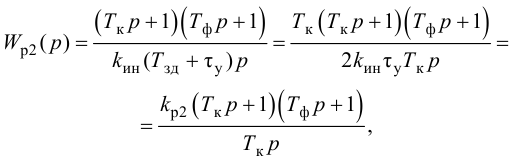
где
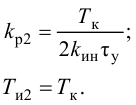
Параметрическая оптимизация типовых систем автоматического регулирования с дифференциатором
Структурная схема типовой двухконтурной САР с дифференциатором представлена на рис. 7.2.
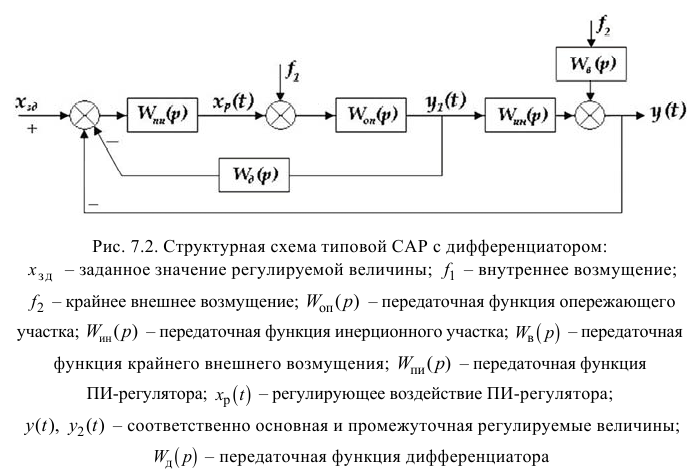
Преобразуем ее в одноконтурную САР путем замены внутреннего контура, состоящего из регулятора, опережающего участка и дифференциатора, эквивалентной передаточной функцией:
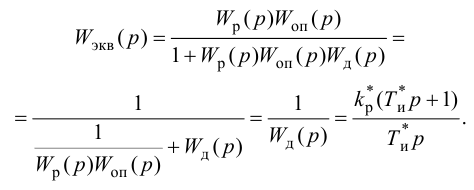
При 
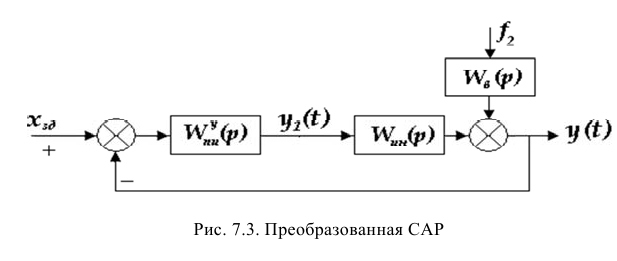
Параметры оптимальной динамической настройки дифференциатора рассчитываем по методу полной компенсации в частном виде для оптимальной отработки крайнего внешнего возмущения 
Согласно МПК в частном виде оптимальные параметры динамической настройки ПИ-регулятора рассчитываем по формулам (6.13):
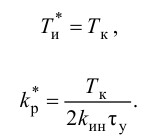
С учетом (7.11) находим параметры динамической настройки дифференциатора через параметры настройки условного ПИ-регу-лятора для оптимальной отработки крайнего внешнего возмущения:
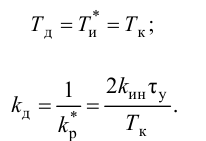
Для оптимальной отработки внутреннего возмущения настройку основного регулятора рассчитывают по структурной схеме внутреннего контура двухконтурной САР, представленной на рис. 7.4.
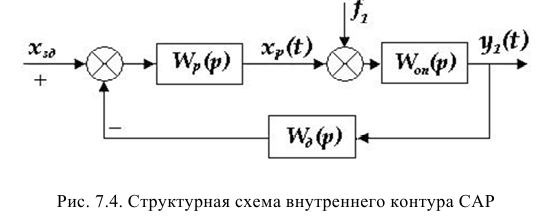
При этом следует учесть, что передаточная функция дифференциатора при достаточно больших значениях времени дифференцирования в момент времени 
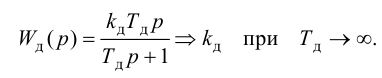
В результате структурная схема САР для рис. 7.4 примет вид, как показано на рис. 7.5.
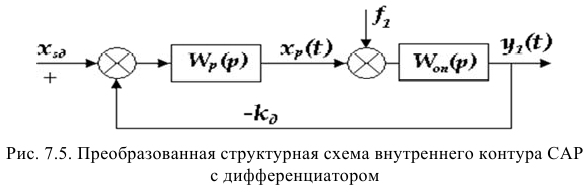
Коэффициент усиления дифференциатора 
Для расчета настройки основного регулятора примем один из методов частичной компенсации на оптимальную отработку внутреннего возмущения 
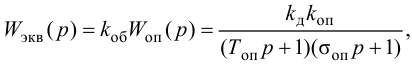
где
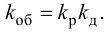
Для упрощения расчета вводим относительные единицы. Находим относительный коэффициент усиления разомкнутой системы:
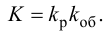
Относительная постоянная времени опережающего участка:
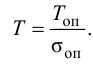
В качестве критерия оптимальности по МЧК принимаем
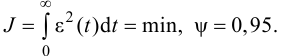
Относительное время интегрирования ПИ-регулятора
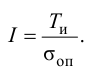
Относительный коэффициент усиления рассчитываем по формуле (7.14) с учетом (7.19):
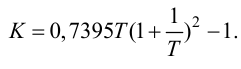
Абсолютное значение коэффициента усиления регулятора 
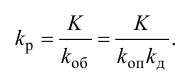
Относительное время интегрирования основного регулятора, согласно методу частичной компенсации, определяют по следующей формуле:
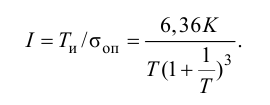
Затем рассчитывают абсолютное время интегрирования регулятора
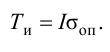
Структурно-параметрическая оптимизация динамических систем
Структурно-параметрическая оптимизация на базе каскадных систем автоматического регулирования
Рассмотрим исходную каскадную систему автоматического регулирования с корректирующим и стабилизирующим регуляторами (см. рис. 7.1).
Выводим передаточную функцию оптимального регулятора, исходя из обратной модели объекта регулирования и оптимальной передаточной функции САР по задающему воздействию. Записываем передаточную функцию замкнутой САР по задающему воздействию:
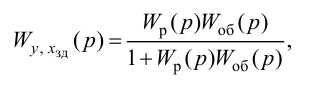
где 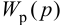
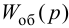
Передаточную функцию САР по задающему воздействию выбираем так, чтобы она соответствовала выбранному критерию качества:
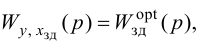
где 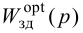
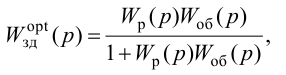
из которой находим передаточную функцию оптимального регулятора:
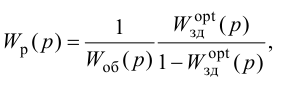
где 
Структуру и оптимальную динамическую настройку внутреннего контура (стабилизирующий регулятор) выбираем на основе передаточной функции опережающего участка объекта регулирования:
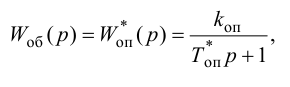
где 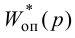
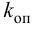
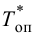
В этом случае критерий оптимальности внутреннего контура при отработке скачка задания 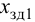
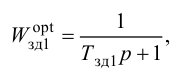
где 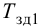
Подставив передаточные функции (8.5) и (8.6) в (8.4), получим оптимальную передаточную функцию стабилизирующего регулятора в виде идеального ПИ-регулятора:
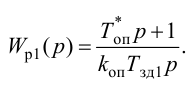
Численное значение единственного параметра его динамической настройки 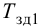
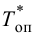
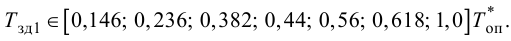
Если передаточную функцию опережающего участка представить в виде инерционного звена второго порядка
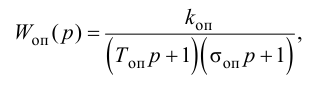
то оптимальная передаточная функция стабилизирующего регулятора на базе передаточной функции (8.4) с учетом заданной передаточной функции
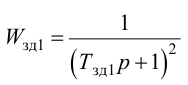
примет вид:
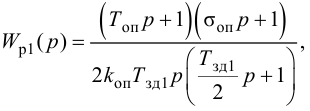
то есть реального ПИД-регулятора, где численное значение постоянной времени критерия оптимальности 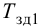
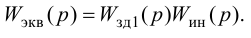
где 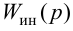
Затем определяют структуру передаточной функции корректирующего регулятора 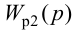
В результате оптимальная передаточная функция корректирующего регулятора с учетом (8.4) примет следующий вид:
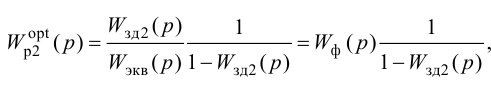
где
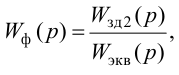
здесь 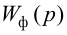
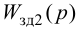
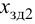
Численное значение 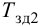
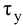
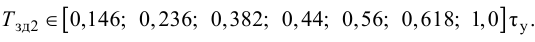
Структурную схему каскадной САР с учетом передаточной функции корректирующего регулятора (8.13) окончательно можно представить в виде, как показано на рис. 8.1.

Пример 8.1.
Структурно-параметрическая оптимизация на базе КСАР для объектов регулирования с самовыравниванием.
Передаточная функция опережающего участка объекта регулирования представлена в виде передаточной функции инерционного звена первого порядка
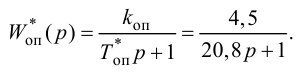
Передаточная функция инерционного участка объекта регулирования представлена в виде передаточной функции инерционного звена первого порядка с условным запаздыванием:
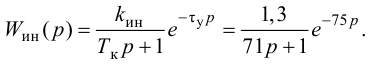
Необходимо определить оптимальную структуру и параметры динамической настройки системы.
Определяем оптимальные параметры динамической настройки стабилизирующего регулятора на основе передаточной функции (8.7):
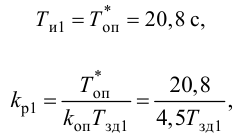
где численные значения 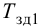
В этом случае передаточная функция стабилизирующего регулятора будет иметь вид
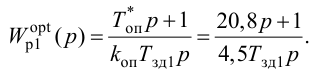
Далее определяем структуру корректирующего устройства на базе передаточной функции эквивалентного объекта (8.12):
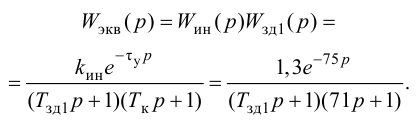
С учетом структуры (8.21) оптимальная передаточная функция САР по задающему воздействию примет вид следующего критерия оптимальной отработки скачка 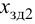
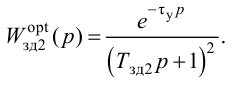
Затем находим оптимальную структуру корректирующего регулятора с учетом формул (8.13) и (8.14):
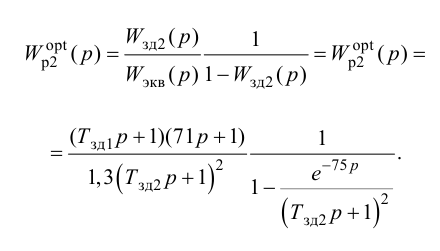
Выбираем следующие численные значения постоянных времени стабилизирующего и корректирующего регуляторов:
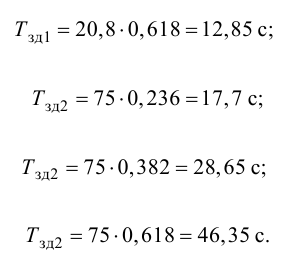
Схема моделирования переходных процессов оптимальной структурно-параметрической каскадной системы автоматического регулирования представлена на рис. 8.1. Графики переходных процессов при основных возмущениях приведены на рис. 8.2.
Из анализа графиков переходных процессов видно, что с уменьшением численного значения 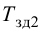
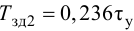
Пример 8.2.
Структурно-параметрическая оптимизация каскадной САР для объектов регулирования без самовыравнивапия (САР уровня воды в барабане парового котла).
Передаточная функция опережающего участка объекта регулирования представлена в виде передаточной функции инерционного звена первого порядка:
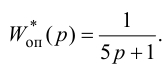
Передаточная функция инерционного участка объекта регулирования представлена в виде передаточной функции идеального интегрирующего звена с запаздыванием:
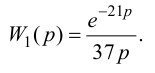
Передаточная функция крайнего внешнего возмущения имеет вид
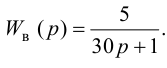
Необходимо определить оптимальную структуру и параметры динамической настройки системы.
Определяем оптимальные параметры динамической настройки стабилизирующего регулятора (8.7) с учетом передаточной функции (8.24):
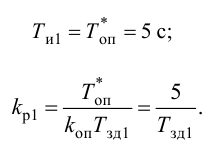
В результате передаточная функция стабилизирующего регулятора примет вид, где численные значения 
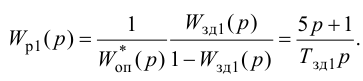
Определяем структуру корректирующего устройства на базе передаточной функции эквивалентного объекта (8.12):
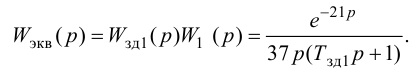
С учетом структуры (8.30) оптимальная передаточная функция САР по задающему воздействию примет вид
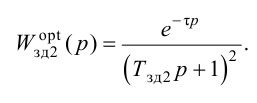
Затем находим оптимальную структуру корректирующего регулятора с учетом формул (8.13) и (8.14):
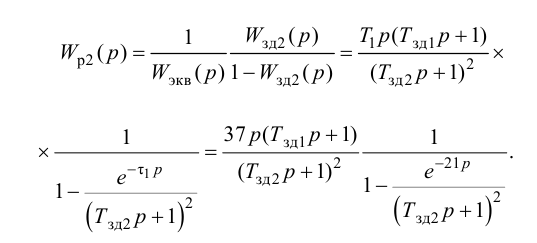
С учетом формул (8.8) и (8.16) выбираем численные значения постоянных времени критериев оптимальности стабилизирующего и корректирующего регуляторов:
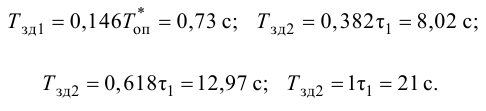
Схема моделирования переходных процессов системы при основных возмущениях представлена на рис. 8.1. Графики переходных процессов при основных возмущениях представлены па рис. 8.3.
Из графиков переходных процессов видно, что с уменьшением численного значения постоянной времени 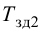
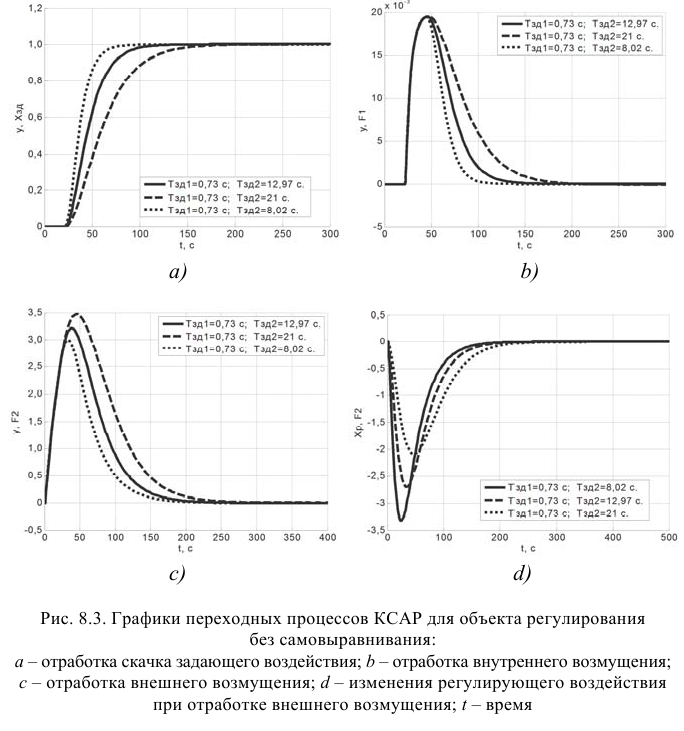
Структурно-параметрическая оптимизация систем автоматического регулирования с использованием модифицированного линейного упредителя Смита и передаточной функции оптимального регулятора
Структурно-параметрическая оптимизация систем автоматического регулирования с использованием модифицированного линейного упредителя Смита и передаточной функции оптимального регулятора позволяет повысить качество регулирования, однако требует реализации неполной и полной модели инерционного участка объекта регулирования с запаздыванием. Структурная схема САР представлена на рис. 8.4.
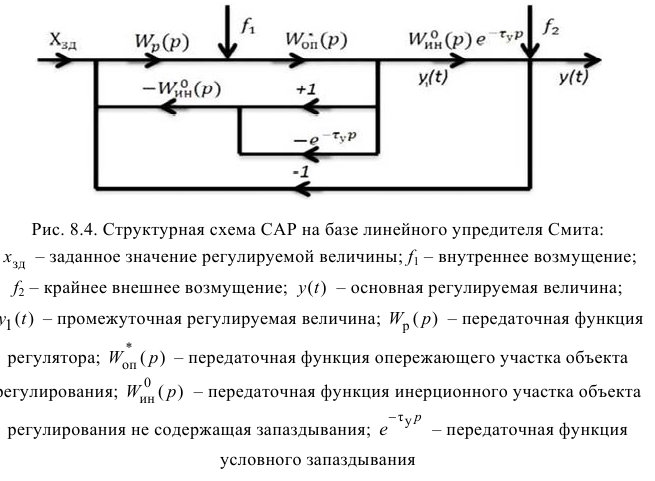
Передаточная функция опережающего участка объекта регулирования имеет вид
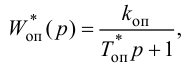
где 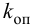
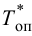
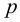
Передаточную функцию инерционного участка объекта регулирования представим в следующем виде:
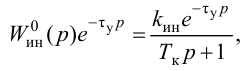
где 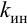
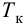
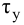
Для выбора структуры основного регулятора используем передаточную функцию оптимального регулятора, которую находим по передаточной функции эквивалентного объекта регулирования:
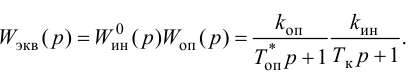
Заданная передаточная функция системы с учетом (8.35) при отработке скачка задания примет вид
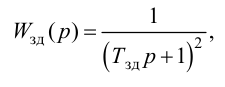
где 
Оптимальная передаточная функция регулятора:
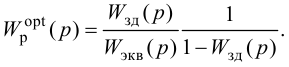
Подставив (8.35) и (8.36) в (8.37), получим передаточную функцию реального ПИД-регулятора:
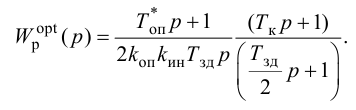
На рис. 8.5 представлены графики переходных процессов САР (рис. 8.4) при различных значениях постоянной времени 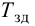
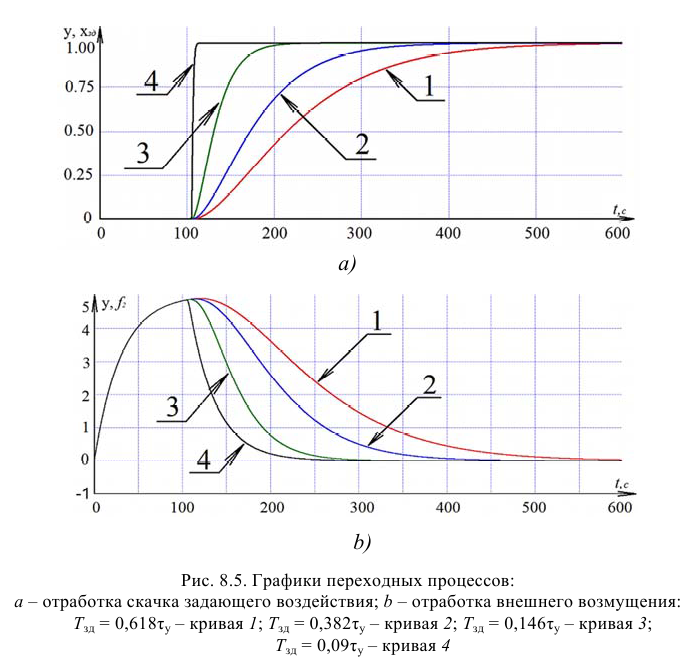
Из графиков переходных процессов видно, что с уменьшением численного значения 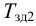
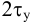
Структурно-параметрическая оптимизация каскадных систем автоматического регулирования с использованием линейного упредителя Смита
Структурная схема каскадной САР с использованием линейного упредителя Смита приведена на рис. 8.6.
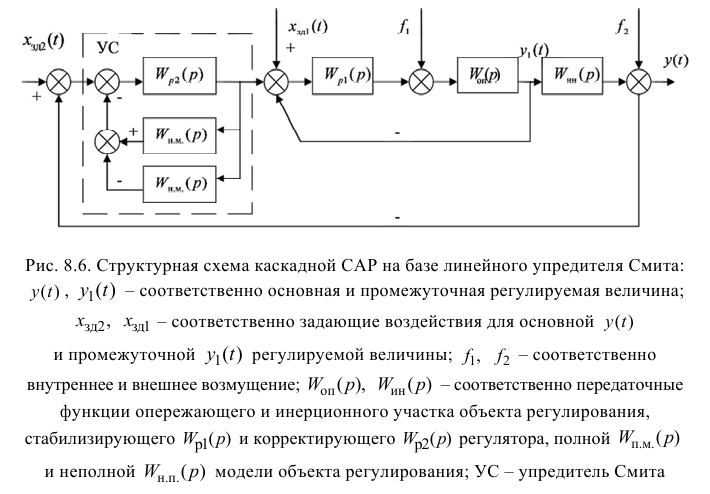
Каскадная система регулирования включает в себя внутренний (стабилизирующий регулятор — опережающий участок объекта регулирования с внутренней обратной связью) и внешний (корректирующий регулятор Смита — внутренний контур — инерционный участок объекта регулирования с главной обратной связью).
Передаточная функция опережающего участка объекта регулирования представлена в виде инерционного звена второго порядка:
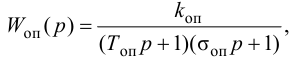
где 
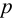
Передаточная функция объекта регулирования задана в виде инерционного звена второго порядка:
где 
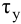
Так как численное значение постоянной времени 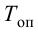
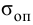
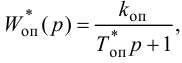
где
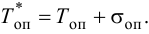
Заданную передаточную функцию замкнутой САР внутреннего контура при отработке задающего сигнала 
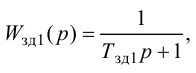
где 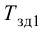
С учетом передаточных функций (8.41), (8.42) оптимальная передаточная функция стабилизирующего регулятора примет следующий вид:
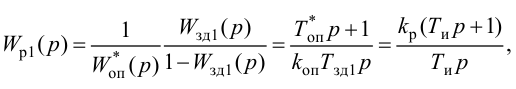
где 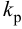
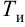
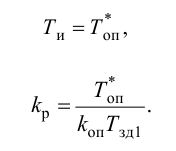
Обозначив заданное время разгона 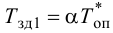
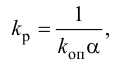
где 
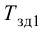
С учетом (8.40), (8.42) передаточная функция полной модели в упредителе Смита примет следующий вид:
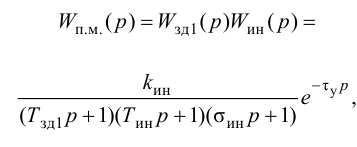
а неполной модели
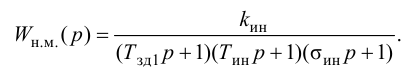
Однако так как численные значения постоянных времени 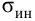
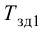
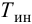
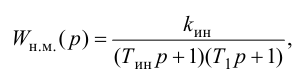
где численное значение постоянной времени
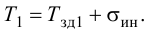
В соответствии с этим заданную передаточную функцию системы регулирования по задающему воздействию целесообразно представить в виде инерционного звена второго порядка с одинаковыми постоянными времени 
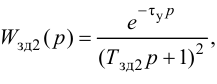
так как при этом переходный процесс в системе будет апериодическим с заданной скоростью изменения регулируемого параметра.
В результате преобразований с учетом передаточных функций (8.50) и (8.51) оптимальная передаточная функция корректирующего регулятора упредителя Смита примет вид реального ПИД-регулятора:
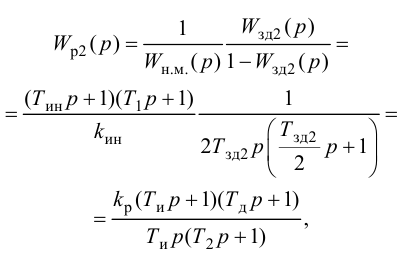
где
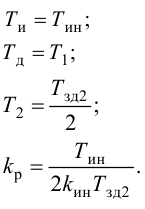
В этом случае за целое в правиле золотого сечения целесообразно принять численное значение условного запаздывания 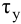
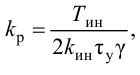
где 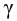
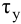
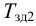
Структурно-параметрическая оптимизация инвариантной системы автоматического регулирования для объектов без самовыравнивания и неизмеримыми возмущениями
Объекты регулирования без самовыравнивания описывают передаточными функциями в виде идеального интегрирующего звена с запаздыванием
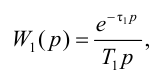
где 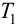
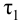
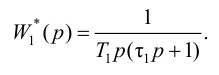
На регулируемую величину влияют возмущающие воздействия. При этом самым опасным является возмущение, приложенное к выходу САР. В инвариантных САР компенсацию влияния возмущения на регулируемую величину достигают за счет введения дополнительного сигнала (с выхода устройства компенсации) на вход регулятора. На рис. 8.7 представлена инвариантная САР с неизмеряемым внешним возмущением.
Для определения структуры и оптимальных параметров динамической настройки регулятора применим метод структурно-параметрической оптимизации на основе передаточной функции оптимального регулятора. Для этого запишем передаточную функцию критерия оптимальности с учетом передаточной функции объекта (8.56):
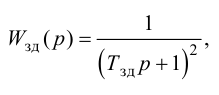
где 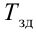
Подставив передаточные функции (8.56) и (8.57) в передаточную функцию оптимального регулятора (8.4), получим
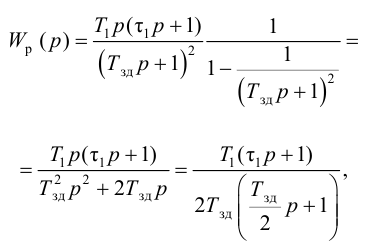
то есть интегродифференцирующее звено.
Динамику объектов регулирования с самовыравииванием описывают передаточными функциями инерционных звеньев, а динамику объектов регулирования без самовыравнивапия — передаточными функциями интегрирующих звеньев. При этом графики переходных функций у данных объектов при единых исходных данных будут совпадать до момента времени 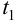
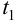
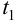
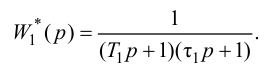
В этом случае передаточная функция регулятора (8.58) будет иметь вид реального ПИД-регулятора:
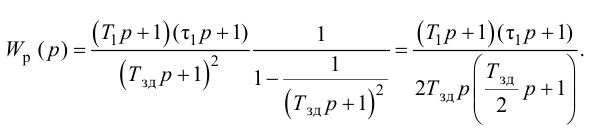
Условие компенсации эквивалентного внешнего возмущения 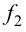
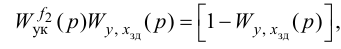
где 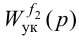
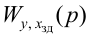
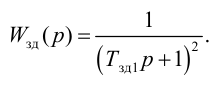
Из равенства (8.61) получаем:
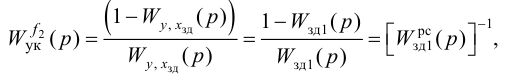
где 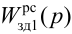
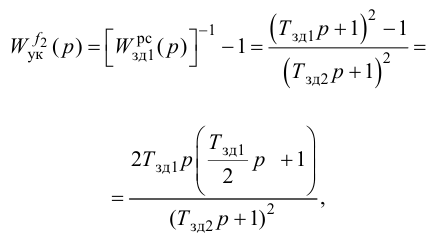
где 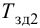
Приняв 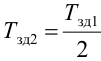
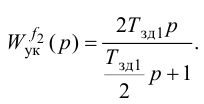
Выбор численных значений 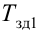
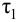
Пример 8.3.
Структурная схема инвариантной САР представлена на рис. 8.7. Передаточная функция объекта регулирования представлена выражением (8.56), где
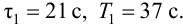
Передаточная функция внешнего возмущения расходом перегретого пара с явлением «набухания уровня» воды в барабане котла имеет следующий вид:
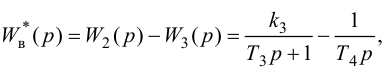
где
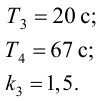
Передаточная функция топочного возмущения имеет вид:
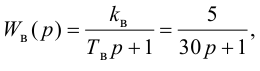
где 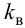
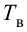
В качестве передаточной функции модели объекта регулирования 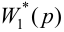
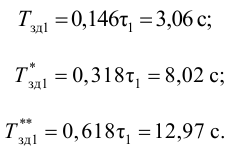
Графики переходных процессов САР с реальным ПИД-регулятором (8.60) при основных возмущениях представлены на рис. 8.8.
Из анализа графиков переходных процессов видно, что с уменьшением численного значения 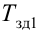
Структурно-параметрическая оптимизация систем автоматического управления нейтронной мощностью ядерного реактора аэс
Структурная схема системы автоматического управления (САУ) нейтронной мощностью ядерного реактора АЭС приведена на рис. 9.1.
Объект регулирования с передаточной функцией 
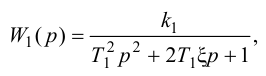
где 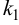
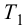
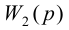
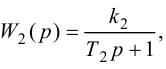
где 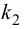
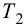
При этом ЛСУ обеспечивает отрицательную обратную связь, работающую в режиме обычного вычитания.
Запаздывание главной обратной связи системы управления соответствует звену чистого запаздывания:
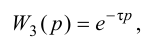
где 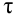
Необходимо определить тип регулятора, обеспечивающего при отработке задающего воздействия требуемое быстродействие и отсутствие или минимальную величину перерегулирования, а также рассчитать значения параметров его оптимальной динамической настройки.
Передаточная функция внутреннего контура системы управления с учетом передаточных функций (9.1) и (9.2) примет следующий вид:
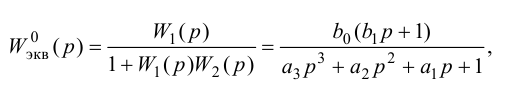
где
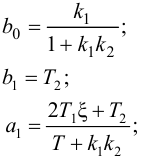
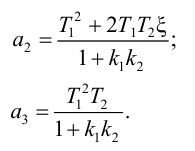
Структурно-параметрическая оптимизация САУ на основе передаточной функции оптимального регулятора
С учетом структуры передаточной функции эквивалентного объекта (9.4) заданная передаточная функция системы управления по задающему воздействию 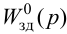
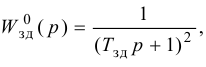
где 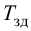
Таким образом, заданная передаточная функция системы управления относительно задающего воздействия (9.10) является критерием оптимальности при выборе структуры системы управления и параметров динамической настройки управляющего устройства.
Передаточная функция оптимального управляющего устройства с учетом запаздывания сигнала главной обратной связи (9.3) представим в следующем виде:
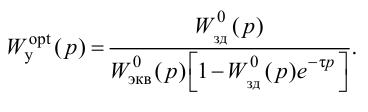
Подставив передаточные функции (9.4) и (9.10) в (9.11), получим искомую передаточную функцию оптимального управляющего устройства:
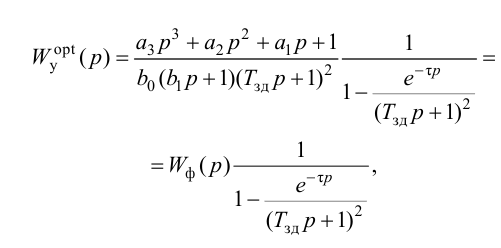
де передаточная функция фильтра
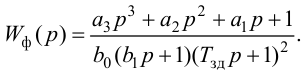
В результате структурная схема моделирования переходных процессов системы управления примет вид, представленный па рис. 9.2.
Графики переходных процессов структурной схемы моделирования переходных процессов САУ нейтронной мощностью ядерного реактора АЭС на основе передаточной функции оптимального регулятора представлены на рис. 9.3.
Из анализа графиков переходных процессов следует, что САУ хорошо отрабатывает задание, однако имеет большую динамическую ошибку при отработке внутреннего возмущения.
Каскадная система автоматического регулирования мощности ядерного реактора АЭС
Для качественной отработки внутреннего возмущения используем каскадную систему автоматического управления (КСАУ), структурная схема которой приведена на рис. 9.4, где внутреннее возмущение оптимально отрабатывается внутренним контуром со стабилизирующим регулятором.
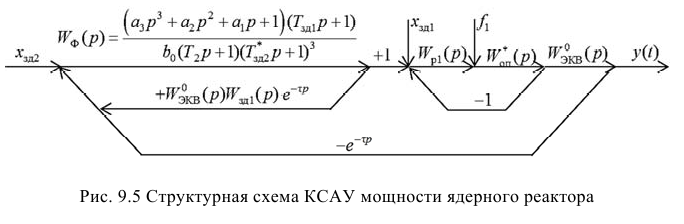
Здесь эквивалентный участок объекта описывается передаточной функцией (9.4).
При этом передаточная функция формирующего задание фильтра
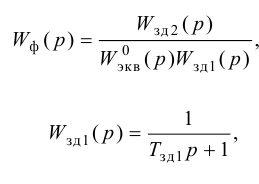
здесь 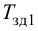
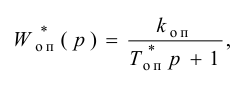
где 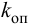
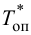
Передаточная функция стабилизирующего регулятора с учетом передаточной функции (9.15) и (9.16) примет вид
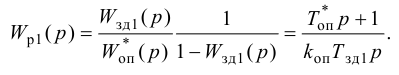
Причем численное значение постоянной времени 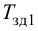
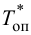
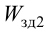
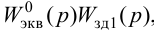
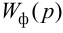
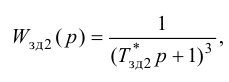
где численное значение постоянной времени 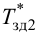
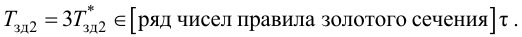
Графики моделирования переходных процессов каскадной системы автоматического управления мощности ядерного реактора АЭС представлены на рис. 9.5.
Из анализа графиков переходных процессов видно, что с уменьшением численного значения 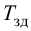
Динамическая точность — система
Cтраница 2
В настоящее время разработан ряд методов, с помощью которых оценивается динамическая точность систем. В качестве показателя динамической точности здесь принимается максимальная динамическая ошибка, имеющая место при наиболее неблагоприятных условиях работы системы.
[16]
Следует учесть, что при большом коэффициенте усиления особенно геобходимо проверить динамическую точность системы и отсутствие недопустимых перерегулирований.
[18]
Третье направление в исследовании качества основывается на интегральных оценках, характеризующих динамическую точность систем регулирования.
[19]
Выражая диаметр трубки через параметры системы и сопоставляя его с требованиями к динамической точности системы, можно определить области значений ее параметров. Таким образом, рассматривается задача воспроизведения сигнала реальным фильтром; возможные обратные связи предполагаются внутренними.
[20]
Полученное выражение показывает, что постоянная времени паразитного апериодического звена Wq может оказывать влияние на динамическую точность системы ( на коэффициенты ошибки) и на другие динамические свойства.
[21]
Значение частоты привязки со п определяется при построении низкочастотной асимптоты желаемой обратной ЛАЧХ разомкнутого ИСП, характеризующей динамическую точность системы при заданном гармоническом управляющем воздействии.
[22]
Задачу оценки поведения САР, которая находится под действием непрерывно меняющихся возмущающих сил / ( t) и управляющего сигнала х0 ( t), называют задачей динамической точности системы. При ограниченных сведениях о возмущениях, приложенных к системе, за показатели динамической точности могут быть приняты следующие величины: максимальная динамическая ошибка, появляющаяся в САР при наиболее неблагоприятных условиях, и среднее квадратическое значение ошибки или функции ошибки. При выборе показателей динамической точности нет необходимости определять величину е ( t) для каждого момента времени, так как важно знать не точное, а некоторое усредненное движение системы и вероятные отклонения от него.
[23]
В случае, когда воздействие, являясь случайным процессом, не может быть заменено типовым сигналом в виде известной функции времени, для оценки качества применяют вероятностные методы, определяя динамическую точность системы по величине среднеквадратичной ошибки или среднеквадратичного отклонения регулируемой величины ( см. гл.
[24]
Под временем регулирования tv понимают время от момента появления отклонения хАх после подачи возмущения в САР до момента, когда это отклонение по абсолютному значению не будет превосходить величины Ал:; Ал: — заданная постоянная, значение которой определяется требованиями к динамической точности системы.
[25]
Эти частоты называются частотами среза замкнутой системы и определяют собой полосу ( интервал) пропускания частот, от которой зависит быстродействие системы. Расширение интервала пропускания частот связано с повышением динамической точности системы.
[26]
Заметим, что ложные срабатывания системы при подходе к экстремуму в ряде случаев, а именно при наличии инерционности у объекта являются положительными явлениями. При этом замедляется скорость подхода системы к экстремуму, что требуется для повышения динамической точности системы.
[27]
Таким образом, запас по фазе внутреннего контура WQWC на левой частоте среза вср.вн. к1 влияет на динамическую точность системы, на добротности системы по ускорению и старшим производным.
[28]
Сельсины могут работать в режиме поворота и в режиме вращения. В первом случае угол рассогласования между осями датчика и приемника после отработки заданного угла поворота характеризует статическую ошибку системы синхронной связи. Во втором случае ротор приемника вращается с той же скоростью, что и ротор датчика, а возникающий между ними в процессе вращения угол рассогласования характеризует динамическую точность системы.
[29]
Асимптотическая ЛАЧХ динамической жесткости, соответствующая ( 8 — 65), дли настройки на технический оптимум а а. Сопоставление этой характеристики с аналогичной характеристикой двухкоптурной системы ( рис. 8 — 17) свидетельствует о том, что введение дополнительного контура регулирования скорости обеспечивает астатическое регулирование скорости по нагрузке и увеличивает точность поддержания постоянства скорости в области низких частот. В области средпечастот-ной асимптоты модуль динамической жесткости остается таким же, как и в двухкоптурной системе, что дает основания предполагать, что при быстрых изменениях нагрузки точность регулирования в астатической системе незначительно отличается от динамической точности более простой двухкоптурной системы.
[30]
Страницы:
1
2
3















































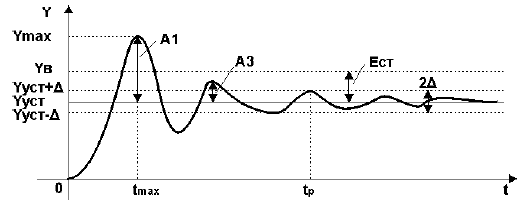
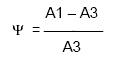
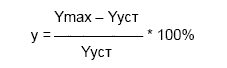
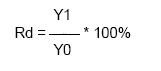
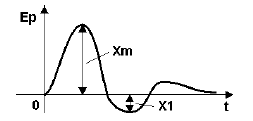
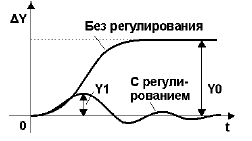
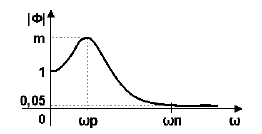
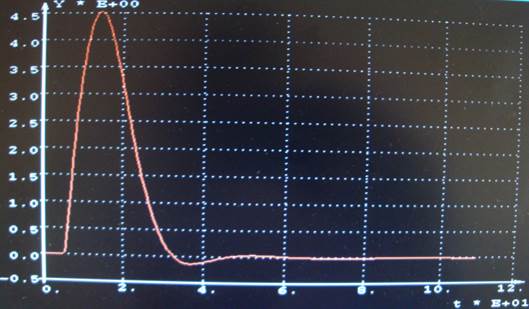
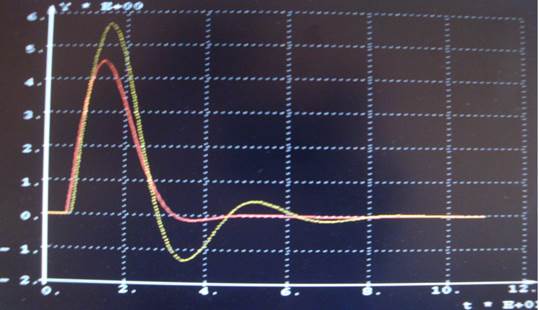
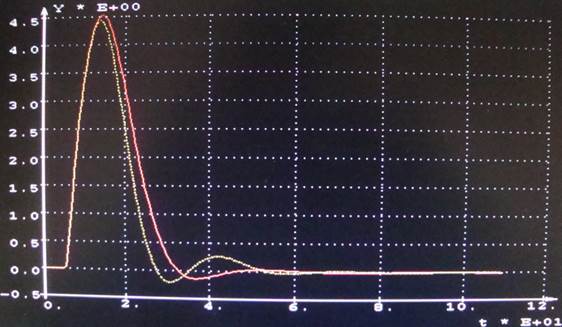
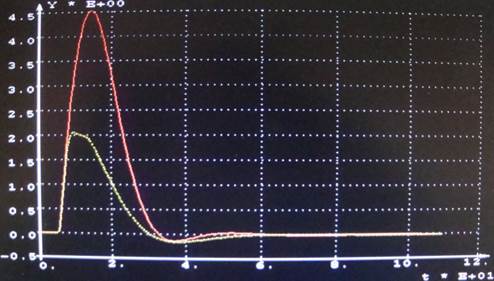
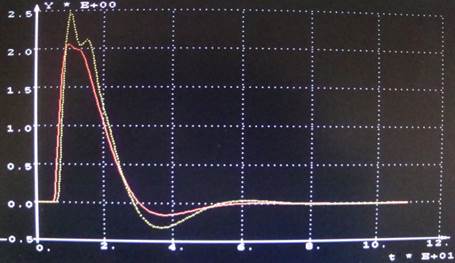
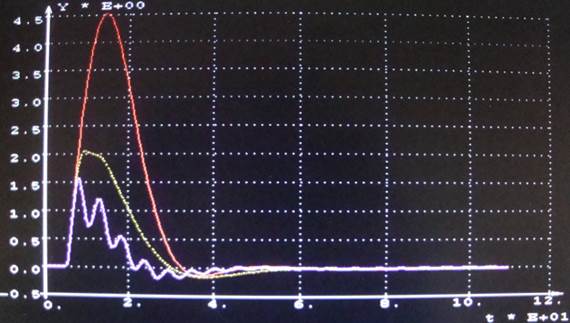


 (задающее воздействие может быть также многомерным).
(задающее воздействие может быть также многомерным).
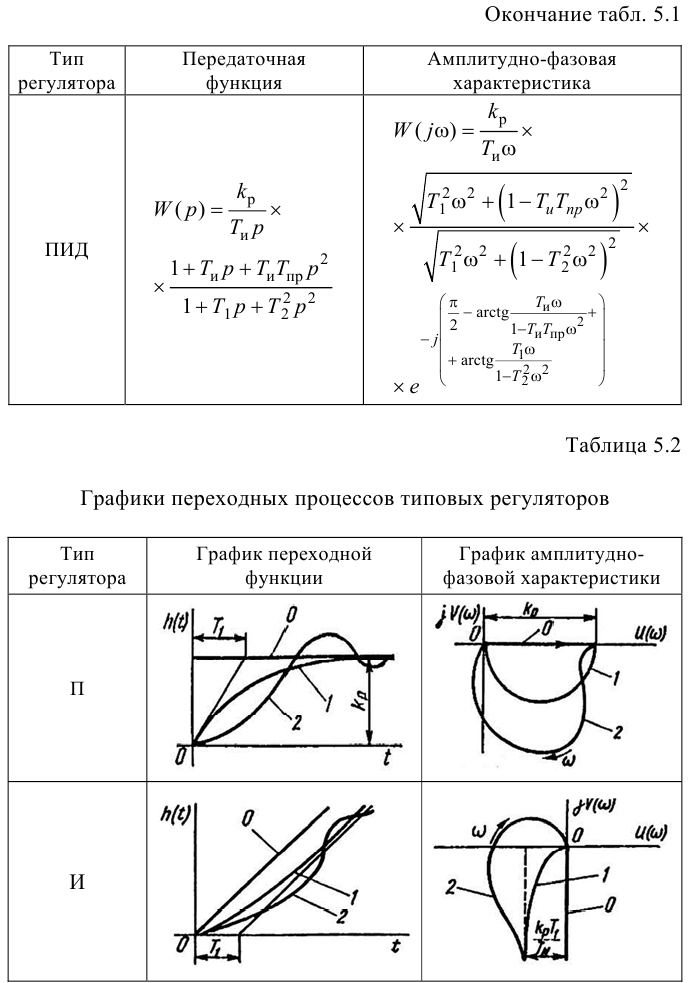
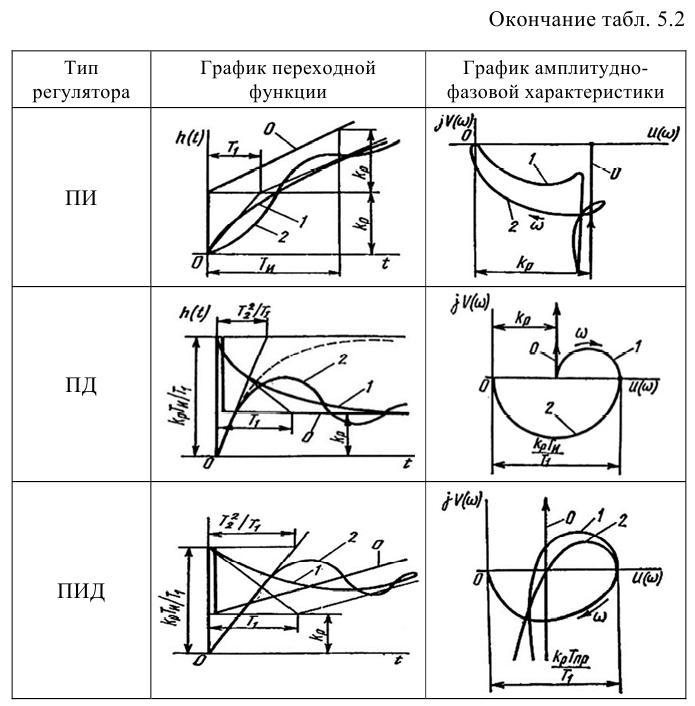



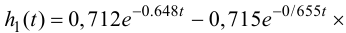
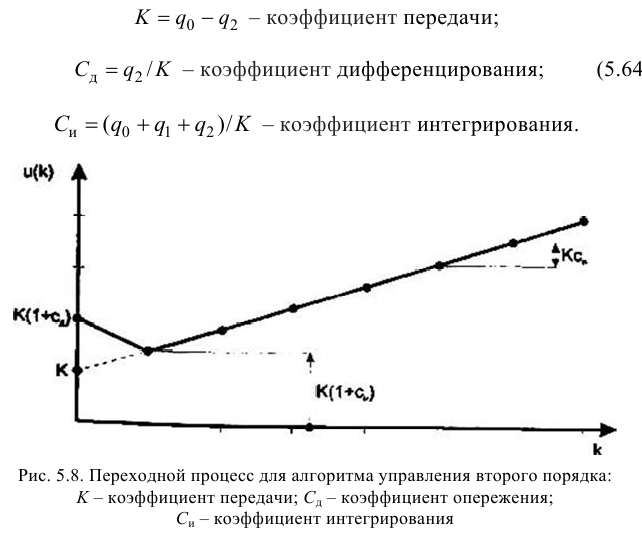
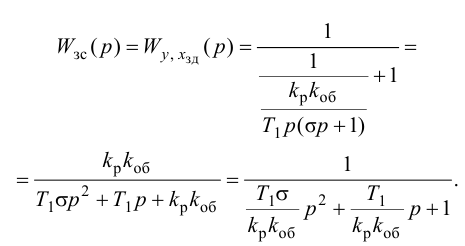
 к переходной характеристике объекта (рис. 6.4) таким образом, чтобы как можно больше точек прямой
к переходной характеристике объекта (рис. 6.4) таким образом, чтобы как можно больше точек прямой 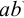 ).
).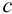 ).
).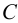 .
.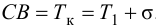 .
.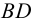 на ось времени.
на ось времени.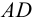 обозначим через
обозначим через 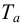 .
.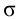 по формуле
по формуле 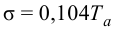 и откладываем влево от точки
и откладываем влево от точки  по оси времени так, чтобы
по оси времени так, чтобы 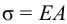 .
.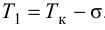 .
.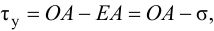 , где
, где 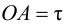 — чистое запаздывание.
— чистое запаздывание.