- sklearn.metrics.confusion_matrix(y_true, y_pred, *, labels=None, sample_weight=None, normalize=None)[source]¶
-
Compute confusion matrix to evaluate the accuracy of a classification.
By definition a confusion matrix (C) is such that (C_{i, j})
is equal to the number of observations known to be in group (i) and
predicted to be in group (j).Thus in binary classification, the count of true negatives is
(C_{0,0}), false negatives is (C_{1,0}), true positives is
(C_{1,1}) and false positives is (C_{0,1}).Read more in the User Guide.
- Parameters:
-
- y_truearray-like of shape (n_samples,)
-
Ground truth (correct) target values.
- y_predarray-like of shape (n_samples,)
-
Estimated targets as returned by a classifier.
- labelsarray-like of shape (n_classes), default=None
-
List of labels to index the matrix. This may be used to reorder
or select a subset of labels.
IfNoneis given, those that appear at least once
iny_trueory_predare used in sorted order. - sample_weightarray-like of shape (n_samples,), default=None
-
Sample weights.
New in version 0.18.
- normalize{‘true’, ‘pred’, ‘all’}, default=None
-
Normalizes confusion matrix over the true (rows), predicted (columns)
conditions or all the population. If None, confusion matrix will not be
normalized.
- Returns:
-
- Cndarray of shape (n_classes, n_classes)
-
Confusion matrix whose i-th row and j-th
column entry indicates the number of
samples with true label being i-th class
and predicted label being j-th class.
References
Examples
>>> from sklearn.metrics import confusion_matrix >>> y_true = [2, 0, 2, 2, 0, 1] >>> y_pred = [0, 0, 2, 2, 0, 2] >>> confusion_matrix(y_true, y_pred) array([[2, 0, 0], [0, 0, 1], [1, 0, 2]])
>>> y_true = ["cat", "ant", "cat", "cat", "ant", "bird"] >>> y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"] >>> confusion_matrix(y_true, y_pred, labels=["ant", "bird", "cat"]) array([[2, 0, 0], [0, 0, 1], [1, 0, 2]])
In the binary case, we can extract true positives, etc as follows:
>>> tn, fp, fn, tp = confusion_matrix([0, 1, 0, 1], [1, 1, 1, 0]).ravel() >>> (tn, fp, fn, tp) (0, 2, 1, 1)
Examples using sklearn.metrics.confusion_matrix¶
Матрица ошибок – это метрика производительности классифицирующей модели Машинного обучения (ML).
Когда мы получаем данные, то после очистки и предварительной обработки, первым делом передаем их в модель и, конечно же, получаем результат в виде вероятностей. Но как мы можем измерить эффективность нашей модели? Именно здесь матрица ошибок и оказывается в центре внимания.
Матрица ошибок – это показатель успешности классификации, где классов два или более. Это таблица с 4 различными комбинациями сочетаний прогнозируемых и фактических значений.
Давайте рассмотрим значения ячеек (истинно позитивные, ошибочно позитивные, ошибочно негативные, истинно негативные) с помощью «беременной» аналогии.
Истинно позитивное предсказание (True Positive, сокр. TP)
Вы предсказали положительный результат, и женщина действительно беременна.
Истинно отрицательное предсказание (True Negative, TN)
Вы предсказали отрицательный результат, и мужчина действительно не беременен.
Ошибочно положительное предсказание (ошибка типа I, False Positive, FN)
Вы предсказали положительный результат (мужчина беременен), но на самом деле это не так.
Ошибочно отрицательное предсказание (ошибка типа II, False Negative, FN)
Вы предсказали, что женщина не беременна, но на самом деле она беременна.
Давайте разберемся в матрице ошибок с помощью арифметики.
Пример. Мы располагаем датасетом пациентов, у которых диагностируют рак. Зная верный диагноз (столбец целевой переменной «Y на самом деле»), хотим усовершенствовать диагностику с помощью модели Машинного обучения. Модель получила тренировочные данные, и на тестовой части, состоящей из 7 записей (в реальных задачах, конечно, больше) и изображенной ниже, мы оцениваем, насколько хорошо прошло обучение.
Модель сделала свои предсказания для каждого пациента и записала вероятности от 0 до 1 в столбец «Предсказанный Y». Мы округляем эти числа, приводя их к нулю или единице, с помощью порога, равного 0,6 (ниже этого значения – ноль, пациент здоров). Результаты округления попадают в столбец «Предсказанная вероятность»: например, для первой записи модель указала 0,5, что соответствует нулю. В последнем столбце мы анализируем, угадала ли модель.
Теперь, используя простейшие формулы, мы рассчитаем Отзыв (Recall), точность результата измерений (Precision), точность измерений (Accuracy), и наконец поймем разницу между этими метриками.
Отзыв
Из всех положительных значений, которые мы предсказали правильно, сколько на самом деле положительных? Подсчитаем, сколько единиц в столбце «Y на самом деле» (4), это и есть сумма TP + FN. Теперь определим с помощью «Предсказанной вероятности», сколько из них диагностировано верно (2), это и будет TP.
$$Отзыв = frac{TP}{TP + FN} = frac{2}{2 + 2} = frac{1}{2}$$
Точность результата измерений (Precision)
В этом уравнении из неизвестных только FP. Ошибочно диагностированных как больных здесь только одна запись.
$$Точностьspaceрезультатаspaceизмерений = frac{TP}{TP + FP} = frac{2}{2 + 1} = frac{2}{3}$$
Точность измерений (Accuracy)
Последнее значение, которое предстоит экстраполировать из таблицы – TN. Правильно диагностированных моделью здоровых людей здесь 2.
$$Точностьspaceизмерений = frac{TP + TN}{Всегоspaceзначений} = frac{2 + 2}{7} = frac{4}{7}$$
F-мера точности теста
Эти метрики полезны, когда помогают вычислить F-меру – конечный показатель эффективности модели.
$$F-мера = frac{2 * Отзыв * Точностьspaceизмерений}{Отзыв + Точностьspaceизмерений} = frac{2 * frac{1}{2} * frac{2}{3}}{frac{1}{2} + frac{2}{3}} = 0,56$$
Наша скромная модель угадывает лишь 56% процентов диагнозов, и такой результат, как правило, считают промежуточным и работают над улучшением точности модели.
SkLearn
С помощью замечательной библиотеки Scikit-learn мы можем мгновенно определить множество метрик, и матрица ошибок – не исключение.
from sklearn.metrics import confusion_matrix
y_true = [2, 0, 2, 2, 0, 1]
y_pred = [0, 0, 2, 2, 0, 2]
confusion_matrix(y_true, y_pred)Выводом будет ряд, состоящий из трех списков:
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])Значения диагонали сверху вниз слева направо [2, 0, 2] – это число верно предсказанных значений.
Фото: @opeleye
| title | date | categories | tags | |||||
|---|---|---|---|---|---|---|---|---|
|
How to create a confusion matrix with Scikit-learn? |
2020-05-05 |
frameworks |
|
After training a supervised machine learning model such as a classifier, you would like to know how well it works.
This is often done by setting apart a small piece of your data called the test set, which is used as data that the model has never seen before.
If it performs well on this dataset, it is likely that the model performs well on other data too — if it is sampled from the same distribution as your test set, of course.
Now, when you test your model, you feed it the data — and compare the predictions with the ground truth, measuring the number of true positives, true negatives, false positives and false negatives. These can subsequently be visualized in a visually appealing confusion matrix.
In today’s blog post, we’ll show you how to create such a confusion matrix with Scikit-learn, one of the most widely used frameworks for machine learning in today’s ML community. By means of an example created with Python, we’ll show you step-by-step how to generate a matrix with which you can visually determine the performance of your model easily.
All right, let’s go! 
[toc]
A confusion matrix in more detail
Training your machine learning model involves its evaluation. In many cases, you have set apart a test set for this.
The test set is a dataset that the trained model has never seen before. Using it allows you to test whether the model has overfit, or adapted to the training data too well, or whether it still generalizes to new data.
This allows you to ensure that your model does not perform very poorly on new data while it still performs really good on the training set. That wouldn’t really work in practice, would it 
Evaluation with a test set often happens by feeding all the samples to the model, generating a prediction. Subsequently, the predictions are compared with the ground truth — or the true targets corresponding to the test set. These can subsequently be used for computing various metrics.
But they can also be used to demonstrate model performance in a visual way.
Here is an example of a confusion matrix:
To be more precise, it is a normalized confusion matrix. Its axes describe two measures:
- The true labels, which are the ground truth represented by your test set.
- The predicted labels, which are the predictions generated by the machine learning model for the features corresponding to the true labels.
It allows you to easily compare how well your model performs. For example, in the model above, for all true labels 1, the predicted label is 1. This means that all samples from class 1 were classified correctly. Great!
For the other classes, performance is also good, but a little bit worse. As you can see, for class 2, some samples were predicted as being part of classes 0 and 1.
In short, it answers the question «For my true labels / ground truth, how well does the model predict?».
It’s also possible to start from a prediction point of view. In this case, the question would change to «For my predicted label, how many predictions are actually part of the predicted class?». It’s the opposite point of view, but could be a valid question in many machine learning cases.
Most preferably, the entire set of true labels is equal to the set of predicted labels. In those cases, you would see zeros everywhere except for the line from the top left to the bottom right. In practice, however, this does not happen often. Likely, the plot is much more scattered, like this SVM classifier where many supporrt vectors are necessary to draw a decision boundary that does not work perfectly, but adequately enough:
Creating a confusion matrix with Python and Scikit-learn
Let’s now see if we can create a confusion matrix ourselves. Today, we will be using Python and Scikit-learn, one of the most widely used frameworks for machine learning today.
Creating a confusion matrix involves various steps:
- Generating an example dataset. This one makes sense: we need data to train our model on. We’ll therefore be generating data first, so that we can make an adequate choice for a ML model class next.
- Picking a machine learning model class. Obviously, if we want to evaluate a model, we need to train a model. We’ll choose a particular type of model first that fits the characteristics of our data.
- Constructing and training the ML model. The consequence of the first two steps is that we end up with a trained model.
- Generating the confusion matrix. Finally, based on the trained model, we can create our confusion matrix.
Software dependencies you need to install
Very briefly, but importantly: if you wish to run this code, you must make sure that you have certain software dependencies installed. Here they are:
- You need to install Python, which is the platform that our code runs on, version 3.6+.
- You need to install Scikit-learn, the machine learning framework that we will be using today:
pip install -U scikit-learn. - You need to install Numpy for numbers processing:
pip install numpy. - You need to install Matplotlib for visualizing the plots:
pip install matplotlib. - Finally, if you wish to generate a plot of decision boundaries (not required), you also need to install Mlxtend:
pip install mlxtend.
[affiliatebox]
Generating an example dataset
The first step is generating an example dataset. We will be using Scikit-learn for this purpose too. First, create a file called confusion-matrix.py, and open it in a code editor. The first thing we do is add the imports:
# Imports
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt
The make_blobs function from Scikit-learn allows us to generate ‘blobs’, or clusters, of samples. Those blobs are centered around some point and are the samples are scattered around this point based on some standard deviation. This gives you flexibility about both the position and the structure of your generated dataset, in turn allowing you to experiment with a variety of ML models without having to worry about the data.
As we will evaluate the model, we need to ensure that the dataset is split between training and testing data. Scikit-learn also allows us to do this, with train_test_split. We therefore import that one too.
Configuration options
Next, we can define a number of configuration options:
# Configuration options
blobs_random_seed = 42
centers = [(0,0), (5,5), (0,5), (2,3)]
cluster_std = 1.3
frac_test_split = 0.33
num_features_for_samples = 4
num_samples_total = 5000
The random seed describes the initialization of the pseudo-random number generator used for generating the blobs of data. As you may know, no random number generator is truly random. What’s more, they are also initialized differently. Configuring a fixed seed ensures that every time you run the script, the random number generator initializes in the same way. If weird behavior occurs, you know that it’s likely not the random number generator.
The centers describe the centers in two-dimensional space of our blobs of data. As you can see, we have 4 blobs today.
The cluster standard deviation describes the standard deviation with which a sample is drawn from the sampling distribution used by the random point generator. We set it to 1.3; a lower number produces clusters that are better separable, and vice-versa.
The fraction of the train/test split determines how much data is split off for testing purposes. In our case, that’s 33% of the data.
The number of features for our samples is 4, and indeed describes how many targets we have: 4, as we have 4 blobs of data.
Finally, the number of samples generated is pretty self-explanatory. We set it to 5000 samples. That’s not too much data, but more than sufficient for the educational purposes of today’s blog post.
Generating the data
Next up is the call to make_blobs and to train_test_split for actually generating and splitting the data:
# Generate data
inputs, targets = make_blobs(n_samples = num_samples_total, centers = centers, n_features = num_features_for_samples, cluster_std = cluster_std)
X_train, X_test, y_train, y_test = train_test_split(inputs, targets, test_size=frac_test_split, random_state=blobs_random_seed)
Saving the data (optional)
Once the data is generated, you may choose to save it to file. This is an optional step — and I include it because I want to re-use the same dataset every time I run the script (e.g. because I am tweaking a visualization). If you use the code below, you can run it once — then, it’s saved in the .npy file. When you subsequently uncomment the np.save call, and possibly also the generate data calls, you’ll always have the same data load from file.
Then, you can tweak away your visualization easily without having to deal with new data all the time 
# Save and load temporarily
np.save('./data_cf.npy', (X_train, X_test, y_train, y_test))
X_train, X_test, y_train, y_test = np.load('./data_cf.npy', allow_pickle=True)
Should you wish to visualize the data, this is of course possible:
# Generate scatter plot for training data
plt.scatter(X_train[:,0], X_train[:,1])
plt.title('Linearly separable data')
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
Picking a machine learning model class
Now that we have our code for generating the dataset, we can take a look at the output to determine what kind of model we could use:
I can derive a few characteristics from this dataset (which, obviously, I also built-in up front 
First of all, the number of features is low: only two — as our data is two-dimensional. This is good, because then we likely don’t face the curse of dimensionality, and a wider range of ML models is applicable.
Next, when inspecting the data from a closer point of view, I can see a gap between what seem to be blobs of data (it is also slightly visible in the diagram above):
This suggests that the data may be separable, and possibly even linearly so (yes, of course, I know this is the case 
Third, and finally, the number of samples is relatively low: only 5.000 samples are present. Neural networks with their relatively large amount of trainable parameters would likely start overfitting relatively quickly, so they wouldn’t be my preferable choice.
However, traditional machine learning techniques to the rescue. A Support Vector Machine, which attempts to construct a decision boundary between separable blobs of data, can be a good candidate here. Let’s give it a try: we’re going to construct and train an SVM and see how well it performs through its confusion matrix.
Constructing and training the ML model
As we have seen in the post linked above, we can also use Scikit-learn to construct and train a SVM classifier. Let’s do so next.
Model imports
First, we’ll have to add a few extra imports to the top of our script:
from sklearn import svm
from sklearn.metrics import plot_confusion_matrix
from mlxtend.plotting import plot_decision_regions
(The Mlxtend one is optional, as we discussed at ‘what you need to install’, but could be useful if you wish to visualize the decision boundary later.)
Training the classifier
First, we initialize the SVM classifier. I’m using a linear kernel because I suspect (actually, I’m confident, as we constructed the data ourselves) that the data is linearly separable:
# Initialize SVM classifier
clf = svm.SVC(kernel='linear')
Then, we fit the training data — starting the training process:
# Fit data
clf = clf.fit(X_train, y_train)
That’s it for training the machine learning model! The classifier variable, or clf, now contains a reference to the trained classifier. By calling clf.predict, you can now generate predictions for new data.
Generating the confusion matrix
But let’s take a look at generating that confusion matrix now. As we discussed, it’s part of the evaluation step, and we use it to visualize its predictive and generalization power on the test set.
Recall that we compare the predictions generated during evaluation with the ground truth available for those inputs.
The plot_confusion_matrix call takes care of this for us, and we simply have to provide it the classifier (clf), the test set (X_test and y_test), a color map and whether to normalize the data.
# Generate confusion matrix
matrix = plot_confusion_matrix(clf, X_test, y_test,
cmap=plt.cm.Blues,
normalize='true')
plt.title('Confusion matrix for our classifier')
plt.show(matrix)
plt.show()
Normalization, here, involves converting back the data into the [0, 1] format above. If you leave out normalization, you get the number of samples that are part of that prediction:
Here are some other visualizations that help us explain the confusion matrix (for the boundary plot, you need to install Mlxtend with pip install mlxtend):
# Get support vectors
support_vectors = clf.support_vectors_
# Visualize support vectors
plt.scatter(X_train[:,0], X_train[:,1])
plt.scatter(support_vectors[:,0], support_vectors[:,1], color='red')
plt.title('Linearly separable data with support vectors')
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
# Plot decision boundary
plot_decision_regions(X_test, y_test, clf=clf, legend=2)
plt.show()
It’s clear that we need many support vectors (the red samples) to generate the decision boundary. Given the relative unclarity of the separability between the data points, this is not unexpected. I’m actually quite satisfied with the performance of the model, as demonstrated by the confusion matrix (relatively blue diagonal line).
The only class that underperforms is class 3, with a score of 0.68. It’s still acceptable, but is lower than preferred. This can be explained by looking at the class in the decision boundary plot. Here, it’s clear that it’s the middle class — the reds. As those samples are surrounded by the other ones, it’s clear that the model has had significant difficulty generating the decision boundary. We might for example counter this by using a different kernel function which takes this into account, ensuring better separability. However, that’s not the core of today’s post.
Full model code
Should you wish to obtain the full model code, that’s of course possible. Here you go 
# Imports
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.metrics import plot_confusion_matrix
from mlxtend.plotting import plot_decision_regions
# Configuration options
blobs_random_seed = 42
centers = [(0,0), (5,5), (0,5), (2,3)]
cluster_std = 1.3
frac_test_split = 0.33
num_features_for_samples = 4
num_samples_total = 5000
# Generate data
inputs, targets = make_blobs(n_samples = num_samples_total, centers = centers, n_features = num_features_for_samples, cluster_std = cluster_std)
X_train, X_test, y_train, y_test = train_test_split(inputs, targets, test_size=frac_test_split, random_state=blobs_random_seed)
# Save and load temporarily
np.save('./data_cf.npy', (X_train, X_test, y_train, y_test))
X_train, X_test, y_train, y_test = np.load('./data_cf.npy', allow_pickle=True)
# Generate scatter plot for training data
plt.scatter(X_train[:,0], X_train[:,1])
plt.title('Linearly separable data')
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
# Initialize SVM classifier
clf = svm.SVC(kernel='linear')
# Fit data
clf = clf.fit(X_train, y_train)
# Generate confusion matrix
matrix = plot_confusion_matrix(clf, X_test, y_test,
cmap=plt.cm.Blues)
plt.title('Confusion matrix for our classifier')
plt.show(matrix)
plt.show()
# Get support vectors
support_vectors = clf.support_vectors_
# Visualize support vectors
plt.scatter(X_train[:,0], X_train[:,1])
plt.scatter(support_vectors[:,0], support_vectors[:,1], color='red')
plt.title('Linearly separable data with support vectors')
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
# Plot decision boundary
plot_decision_regions(X_test, y_test, clf=clf, legend=2)
plt.show()
[affiliatebox]
Summary
That’s it for today! In this blog post, we created a confusion matrix with Python and Scikit-learn. After studying what a confusion matrix is, and how it displays true positives, true negatives, false positives and false negatives, we gave a step-by-step example for creating one yourself.
The example included generating a dataset, picking a suitable machine learning model for the dataset, constructing, configuring and training it, and finally interpreting the results i.e. the confusion matrix. This way, you should be able to understand what is happening and why I made certain choices.
I hope you’ve learnt something from today’s blog post! 
Thank you for reading MachineCurve today and happy engineering! 😎
[scikitbox]
References
Raschka, S. (n.d.). Home — mlxtend. Site not found · GitHub Pages. https://rasbt.github.io/mlxtend/
Scikit-learn. (n.d.). scikit-learn: machine learning in Python — scikit-learn 0.16.1 documentation. Retrieved May 3, 2020, from https://scikit-learn.org/stable/index.html
Scikit-learn. (n.d.). 1.4. Support vector machines — scikit-learn 0.22.2 documentation. scikit-learn: machine learning in Python — scikit-learn 0.16.1 documentation. Retrieved May 3, 2020, from https://scikit-learn.org/stable/modules/svm.html#classification
Scikit-learn. (n.d.). Confusion matrix — scikit-learn 0.22.2 documentation. scikit-learn: machine learning in Python — scikit-learn 0.16.1 documentation. Retrieved May 5, 2020, from https://scikit-learn.org/stable/auto_examples/model_selection/plot_confusion_matrix.html
Scikit-learn. (n.d.). Sklearn.metrics.plot_confusion_matrix — scikit-learn 0.22.2 documentation. scikit-learn: machine learning in Python — scikit-learn 0.16.1 documentation. Retrieved May 5, 2020, from https://scikit-learn.org/stable/modules/generated/sklearn.metrics.plot_confusion_matrix.html#sklearn.metrics.plot_confusion_matrix
In this Python tutorial, we will learn How Scikit learn confusion matrix works in Python and we will also cover different examples related to Scikit learn confusion matrix. And, we will cover these topics.
- Scikit learn confusion matrix
- Scikit learn confusion matrix example
- Scikit learn confusion matrix plot
- Scikit learn confusion matrix accuracy
- Scikit learn confusion matrix multiclass
- Scikit learn confusion matrix display
- Scikit learn confusion matrix labels
- Scikit learn confusion matrix normalize
In this section, we will learn about how the Scikit learn confusion matrix works in python.
- Scikit learn confusion matrix is defined as a technique to calculate the performance of classification.
- The confusion matrix is also used to predict or summarise the result of the classification problem.
Code:
- y_true = [2, 0, 0, 2, 0, 1] is used to get the true value.
- y_pred = [0, 0, 2, 0, 0, 2] is used to get the predicted value.
- confusion_matrix(y_true, y_pred) is used to evaluate the confusion matrix.
from sklearn.metrics import confusion_matrix
y_true = [2, 0, 0, 2, 0, 1]
y_pred = [0, 0, 2, 0, 0, 2]
confusion_matrix(y_true, y_pred)Output:
After running the above code, we get the following output in which we can see that the confusion matrix value is printed on the screen.

Read: Scikit learn Image Processing
Scikit learn confusion matrix example
In this section, we will learn about how Scikit learn confusion matrix example works in python.
- Scikit learn confusion matrix example is defined as a technique to summarise the result of the classification.
- The confusion matrix also predicted the number of correct and incorrect predictions of the classification model.
Code:
In the following code, we will import some libraries from which we can make the confusion matrix.
- iris = datasets.load_iris() is used to load the iris data.
- class_names = iris.target_names is used to get the target names.
- x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=0) is used to split the data set into train and test data.
- classifier = svm.SVC(kernel=”linear”, C=0.02).fit(x_train, y_train) is used to fit the model.
- ConfusionMatrixDisplay.from_estimator() is used to plot the confusion matrix.
- print(display.confusion_matrix) is used to print the confusion matrix.
import numpy as num
import matplotlib.pyplot as plot
from sklearn import svm, datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import ConfusionMatrixDisplay
iris = datasets.load_iris()
x = iris.data
y = iris.target
class_names = iris.target_names
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=0)
classifier = svm.SVC(kernel="linear", C=0.02).fit(x_train, y_train)
num.set_printoptions(precision=2)
title_options = [
("Confusion matrix, without normalization", None),
("Normalized confusion matrix", "true"),
]
for title, normalize in title_options:
display = ConfusionMatrixDisplay.from_estimator(
classifier,
x_test,
y_test,
display_labels=class_names,
cmap=plot.cm.Blues,
normalize=normalize,
)
display.ax_.set_title(title)
print(title)
print(display.confusion_matrix)
plot.show()Output:
In the following output, we can see that the result of the classification is summarised on the screen with help of a confusion matrix.

Read: Scikit learn non-linear [Complete Guide]
Scikit learn confusion matrix plot
In this section, we will learn about how Scikit learn confusion matrix plot in python.
- Scikit learn confusion matrix plot is used to plot the graph on the screen to summarise the result of the model.
- It is used to plot the graph to predict the number of correct or incorrect predictions of the model.
Code:
In the following code, we will import some libraries from which we can plot the confusion matrix on the screen.
- x, y = make_classification(random_state=0) is used to make classification.
- x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=0) is used to split the data set into train and test set.
- classifier.fit(x_train, y_train) is used to fit the model.
- plot_confusion_matrix(classifier, x_test, y_test) is used to plot the confusion matrix on the screen.
import matplotlib.pyplot as plot
from sklearn.datasets import make_classification
from sklearn.metrics import plot_confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
x, y = make_classification(random_state=0)
x_train, x_test, y_train, y_test = train_test_split(
x, y, random_state=0)
classifier = SVC(random_state=0)
classifier.fit(x_train, y_train)
SVC(random_state=0)
plot_confusion_matrix(classifier, x_test, y_test)
plot.show()Output:
After running the above code, we get the following output in which we can see that the confusion matrix is plotted on the screen.

Read: Scikit learn KNN Tutorial
Scikit learn confusion matrix accuracy
In this section, we will learn about Scikit learn confusion matrix accuracy of the model in python.
Scikit learn confusion matrix accuracy is used to calculate the accuracy of the matrix how accurate our model result.
Code:
In the following code, we will import some libraries from which we can calculate the accuracy of the model.
- y_pred = [1, 3, 2, 0] is used to predict the predicted value.
- y_true = [0, 1, 2, 3] is used to predict the true value.
- accuracy_score(y_true, y_pred) is used to predict the accuracy score.
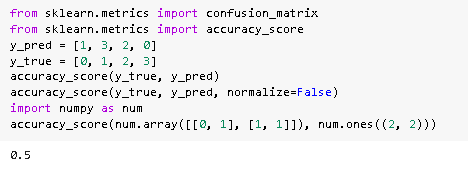
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
y_pred = [1, 3, 2, 0]
y_true = [0, 1, 2, 3]
accuracy_score(y_true, y_pred)
accuracy_score(y_true, y_pred, normalize=False)
import numpy as num
accuracy_score(num.array([[0, 1], [1, 1]]), num.ones((2, 2)))Output:
After running the above code, we get the following output in which we can see that the confusion matrix accuracy score is printed on the screen.
Read: Scikit learn Sentiment Analysis
Scikit learn confusion matrix multiclass
In this section, we will learn about how scikit learn confusion matrix multiclass works in python.
Scikit learn confusion matrix multi-class is defined as a problem of classifying illustration of one of the three or more classes.
Code:
In the following code, we will import some libraries from which we can make a confusion matrix multiclass.
- df = pd.read_csv(“IRIS.csv”) is used to load the dataset.
- df.dtypes is used to select the types of data.
#importing packages
import pandas as pds
import numpy as num
import seaborn as sb
import matplotlib.pyplot as plot
df = pd.read_csv("IRIS.csv")
df.head()
df.dtypes
- x = df.drop([‘species’], axis=1) is used to separating independent variable and dependent variable.
- print(x.shape) is used to print the shape of the dataset.
#Separating independant variable and dependent variable("Species")
x = df.drop(['species'], axis=1)
y = df['species']
print(x.shape)
print(y.shape)
- x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=0) is used to split the dataset into train and test set.
- print(x_train.shape) is used to print the shape of the train set.
- print(x_test.shape) is used to print the shape of the test set.
# Splitting the dataset to Train and test
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=0)
print(x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)
- classifier = SVC(kernel = ‘linear’).fit(x_train,y_train) is used to training the classifier from x train and y train.
- cm = confusion_matrix(y_test, y_pred) is used to creating the confusion matrix.
- cm_df = pd.DataFrame() is used to create the data frame.
- plot.figure(figsize=(5,4)) is used to plot the figure.
from sklearn.svm import SVC
from sklearn.metrics import confusion_matrix
classifier = SVC(kernel = 'linear').fit(x_train,y_train)
classifier.predict(x_train)
y_pred = classifier.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
cm_df = pd.DataFrame(cm,
index = ['SETOSA','VERSICOLR','VIRGINICA'],
columns = ['SETOSA','VERSICOLR','VIRGINICA'])
plot.figure(figsize=(5,4))
sb.heatmap(cm_df, annot=True)
plot.title('Confusion Matrix')
plot.ylabel('Actal Values')
plot.xlabel('Predicted Values')
plot.show()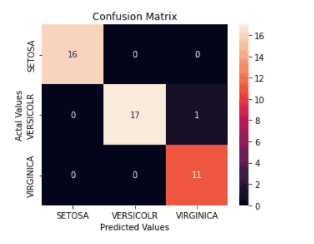
Read: Scikit learn Gradient Descent
Scikit learn confusion matrix display
In this section, we will learn about how Scikit learn confusion matrix display works in python.
Scikit learn confusion matrix display is defined as a matrix in which i,j is equal to the number of observations are forecast to be in a group.
Code:
In the following code, we will learn to import some libraries from which we can see how the confusion matrix is displayed on the screen.
- x, y = make_classification(random_state=0) is used to make classification.
- x_train, x_test, y_train, y_test = train_test_split(x, y,random_state=0) is used to split the dataset into train and test data.
- classifier.fit(x_train, y_train) is used to fit the data.
- predictions = classifier.predict(x_test) is used to predict the data.
- display=ConfusionMatrixDisplay(confusion_matrix=cm,display_labels=classifier.classes_) is used to display the confusion matrix.
- display.plot() is used to plot the matrix.
import matplotlib.pyplot as plot
from sklearn.datasets import make_classification
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
x, y = make_classification(random_state=0)
x_train, x_test, y_train, y_test = train_test_split(x, y,
random_state=0)
classifier = SVC(random_state=0)
classifier.fit(x_train, y_train)
SVC(random_state=0)
predictions = classifier.predict(x_test)
cm = confusion_matrix(y_test, predictions, labels=classifier.classes_)
display = ConfusionMatrixDisplay(confusion_matrix=cm,
display_labels=classifier.classes_)
display.plot()
plot.show()Output:
After running the above code, we get the following output in which we can see that a confusion matrix is displayed on the screen.

Read: Scikit learn Classification Tutorial
Scikit learn confusion matrix labels
In this section, we will learn how Scikit learn confusion matrix labels works in python.
Scikit learn confusion matrix label is defined as a two-dimension array that contrasts a predicted group of labels with true labels.
Code:
In the following code, we will import some libraries to know how scikit learn confusion matrix labels works.
- y_true = num.array([[1, 0, 0],[0, 1, 1]]) is used to collect the true labels in the array.
- y_pred = num.array([[1, 0, 1],[0, 1, 0]]) is used to collect the predicted labelsin the array.
- multilabel_confusion_matrix(y_true, y_pred) is used to get multilabel confusion matrix.
import numpy as num
from sklearn.metrics import multilabel_confusion_matrix
y_true = num.array([[1, 0, 0],
[0, 1, 1]])
y_pred = num.array([[1, 0, 1],
[0, 1, 0]])
multilabel_confusion_matrix(y_true, y_pred)Output:
After running the above code, we get the following output in which we can see that the confusion matrix labels are printed on the screen.

Read: Scikit learn Hyperparameter Tuning
Scikit learn confusion matrix normalize
In this section, we will learn about how scikit learn confusion matrix normalize works in python.
Scikit learn confusion matrix normalize is defined as a process that represents one sample is present in each group.
Code:
In the following code, we will import some libraries from which we can normalize the matrix.
- iris = datasets.load_iris() is used to load the data.
- x_train, x_test, y_train, y_test = train_test_split(X, y, random_state=0) is used use to split the dataset into train and test data.
- classifier = svm.SVC(kernel=’linear’, C=0.01) is used as a classifier.
- y_pred = classifier.fit(x_train, y_train).predict(x_test) is used to fit the model.
- cm = confusion_matrix(y_true, y_pred) is used to compute the confusion matrix.
- classes = classes[unique_labels(y_true, y_pred)] is used of label that appear in the data.
- figure, axis = plot.subplots() is used to plot the figure on the screen.
- plot.setp(axis.get_xticklabels(), rotation=45, ha=”right”,rotation_mode=”anchor”) is used to set the alignment and rotate the ticks.
- plot_confusion_matrix(y_test, y_pred, classes=class_names, normalize=True, title=’Normalized confusion matrix’) is used to plot the normalized confusion matrix.
import numpy as num
import matplotlib.pyplot as plot
from sklearn import svm, datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
from sklearn.utils.multiclass import unique_labels
iris = datasets.load_iris()
x_digits = iris.data
y = iris.target
class_names = iris.target_names
x_train, x_test, y_train, y_test = train_test_split(X, y, random_state=0)
classifier = svm.SVC(kernel='linear', C=0.01)
y_pred = classifier.fit(x_train, y_train).predict(x_test)
def plot_confusion_matrix(y_true, y_pred, classes,
normalize=False,
title=None,
cmap=plot.cm.Blues):
if not title:
if normalize:
title = 'Normalized confusion matrix'
cm = confusion_matrix(y_true, y_pred)
classes = classes[unique_labels(y_true, y_pred)]
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, num.newaxis]
print("Normalized confusion matrix")
print(cm)
figure, axis = plot.subplots()
im = axis.imshow(cm, interpolation='nearest', cmap=cmap)
axis.figure.colorbar(im, ax=axis)
axis.set(xticks=num.arange(cm.shape[1]),
yticks=num.arange(cm.shape[0]),
xticklabels=classes, yticklabels=classes,
title=title,
ylabel='True label',
xlabel='Predicted label')
plot.setp(axis.get_xticklabels(), rotation=45, ha="right",
rotation_mode="anchor")
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
axis.text(j, i, format(cm[i, j], fmt),
ha="center", va="center",
color="cyan" if cm[i, j] > thresh else "red")
figure.tight_layout()
return axis
plot_confusion_matrix(y_test, y_pred, classes=class_names, normalize=True,
title='Normalized confusion matrix')
plot.show()Output:
In the following code, we will see a normalized confusion matrix array is created, and also a normalized confusion matrix graph is plotted on the screen.

Also, take a look at some more Scikit learn tutorials.
- Scikit learn Linear Regression
- Scikit learn Feature Selection
- Scikit learn Ridge Regression
- Scikit learn Random Forest
So, in this tutorial we discussed Scikit learn confusion matrix and we have also covered different examples related to its implementation. Here is the list of examples that we have covered.
- Scikit learn confusion matrix
- Scikit learn confusion matrix example
- Scikit learn confusion matrix plot
- Scikit learn confusion matrix accuracy
- Scikit learn confusion matrix multiclass
- Scikit learn confusion matrix display
- Scikit learn confusion matrix labels
- Scikit learn confusion matrix normalize
I am Bijay Kumar, a Microsoft MVP in SharePoint. Apart from SharePoint, I started working on Python, Machine learning, and artificial intelligence for the last 5 years. During this time I got expertise in various Python libraries also like Tkinter, Pandas, NumPy, Turtle, Django, Matplotlib, Tensorflow, Scipy, Scikit-Learn, etc… for various clients in the United States, Canada, the United Kingdom, Australia, New Zealand, etc. Check out my profile.
In machine Learning, Classification is the process of categorizing a given set of data into different categories. In Machine Learning, To measure the performance of the classification model we use the confusion matrix.
Confusion Matrix
A confusion matrix is a matrix that summarizes the performance of a machine learning model on a set of test data. It is often used to measure the performance of classification models, which aim to predict a categorical label for each input instance. The matrix displays the number of true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN) produced by the model on the test data.
For binary classification, the matrix will be of a 2X2 table, For multi-class classification, the matrix shape will be equal to the number of classes i.e for n classes it will be nXn.
A 2X2 Confusion matrix is shown below for the image recognization having a Dog image or Not Dog image.
|
Actual |
|||
|---|---|---|---|
|
Dog |
Not Dog |
||
|
Predicted |
Dog |
True Positive |
False Positive |
|
Not Dog |
False Negative |
True Negative |
- True Positive (TP): It is the total counts having both predicted and actual values are Dog.
- True Negative (TN): It is the total counts having both predicted and actual values are Not Dog.
- False Positive (FP): It is the total counts having prediction is Dog while actually Not Dog.
- False Negative (FN): It is the total counts having prediction is Not Dog while actually, it is Dog.
Example
|
Index |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|---|---|---|---|---|---|---|---|---|---|---|
|
Actual |
Dog |
Dog |
Dog |
Not Dog |
Dog |
Not Dog |
Dog |
Dog |
Not Dog |
Not Dog |
|
Predicted |
Dog |
Not Dog |
Dog |
Not Dog |
Dog |
Dog |
Dog |
Dog |
Not Dog |
Not Dog |
|
Result |
TP |
FN |
TP |
TN |
TP |
FP |
TP |
TP |
TN |
TN |
- Actual Dog Counts = 6
- Actual Not Dog Counts = 4
- True Positive Counts = 5
- False Positive Counts = 1
- True Negative Counts = 3
- False Negative Counts = 1
|
Actual |
|||
|---|---|---|---|
|
Dog |
Not Dog |
||
|
Predicted |
Dog |
True Positive |
False Positive |
|
Not Dog |
False Negative |
True Negative |
Confusion Matrix
Implementations of Confusion Matrix in Python
Steps:
- Import the necessary libraries like Numpy, confusion_matrix from sklearn.metrics, seaborn, and matplotlib.
- Create the NumPy array for actual and predicted labels.
- compute the confusion matrix.
- Plot the confusion matrix with the help of the seaborn heatmap.
Python3
import numpy as np
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
actual = np.array(
['Dog','Dog','Dog','Not Dog','Dog','Not Dog','Dog','Dog','Not Dog','Not Dog'])
predicted = np.array(
['Dog','Not Dog','Dog','Not Dog','Dog','Dog','Dog','Dog','Not Dog','Not Dog'])
cm = confusion_matrix(actual,predicted)
sns.heatmap(cm,
annot=True,
fmt='g',
xticklabels=['Dog','Not Dog'],
yticklabels=['Dog','Not Dog'])
plt.ylabel('Prediction',fontsize=13)
plt.xlabel('Actual',fontsize=13)
plt.title('Confusion Matrix',fontsize=17)
plt.show()
Output:
Confusion Matrix
From the confusion matrix, we can find the following metrics
Accuracy: Accuracy is used to measure the performance of the model. It is the ratio of Total correct instances to the total instances.
For the above case:
Accuracy = (5+3)/(5+3+1+1) = 8/10 = 0.8
Precision: Precision is a measure of how accurate a model’s positive predictions are. It is defined as the ratio of true positive predictions to the total number of positive predictions made by the model
For the above case:
Precision = 5/(5+1) =5/6 = 0.8333
Recall: Recall measures the effectiveness of a classification model in identifying all relevant instances from a dataset. It is the ratio of the number of true positive (TP) instances to the sum of true positive and false negative (FN) instances.
For the above case:
Recall = 5/(5+1) =5/6 = 0.8333
F1-Score: F1-score is used to evaluate the overall performance of a classification model. It is the harmonic mean of precision and recall,
For the above case:
F1-Score: = (2* 0.8333* 0.8333)/( 0.8333+ 0.8333) = 0.8333
Example:2 Binary Classifications for Breast Cancer
Python3
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
X, y= load_breast_cancer(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y,test_size=0.25)
tree = DecisionTreeClassifier(random_state=23)
tree.fit(X_train, y_train)
y_pred = tree.predict(X_test)
cm = confusion_matrix(y_test,y_pred)
sns.heatmap(cm,
annot=True,
fmt='g',
xticklabels=['malignant', 'benign'],
yticklabels=['malignant', 'benign'])
plt.ylabel('Prediction',fontsize=13)
plt.xlabel('Actual',fontsize=13)
plt.title('Confusion Matrix',fontsize=17)
plt.show()
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy :", accuracy)
precision = precision_score(y_test, y_pred)
print("Precision :", precision)
recall = recall_score(y_test, y_pred)
print("Recall :", recall)
F1_score = f1_score(y_test, y_pred)
print("F1-score :", F1_score)
Output:
Confusion Matrix for Breast cancer Classifications
Accuracy : 0.9230769230769231 Precision : 1.0 Recall : 0.8842105263157894 F1-score : 0.9385474860335195
Example 3: Multi-Class Classifications for Handwritten Digit dataset
Python3
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
X, y= load_digits(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y,test_size=0.25)
clf = RandomForestClassifier(random_state=23)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
cm = confusion_matrix(y_test,y_pred)
sns.heatmap(cm,
annot=True,
fmt='g')
plt.ylabel('Prediction',fontsize=13)
plt.xlabel('Actual',fontsize=13)
plt.title('Confusion Matrix',fontsize=17)
plt.show()
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy :", accuracy)
Output:
Confusion Matrix for Handwritten Digit Classifications
Accuracy : 0.9844444444444445
Last Updated :
21 Mar, 2023
Like Article
Save Article















.png)
.png)
.png)