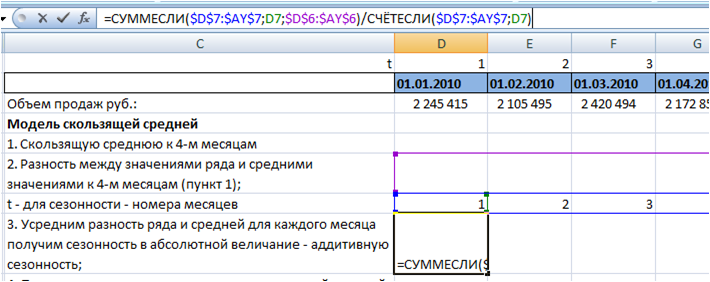
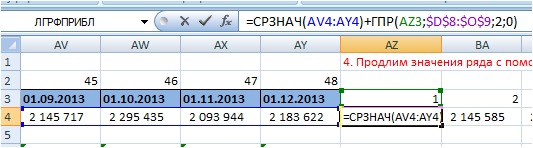
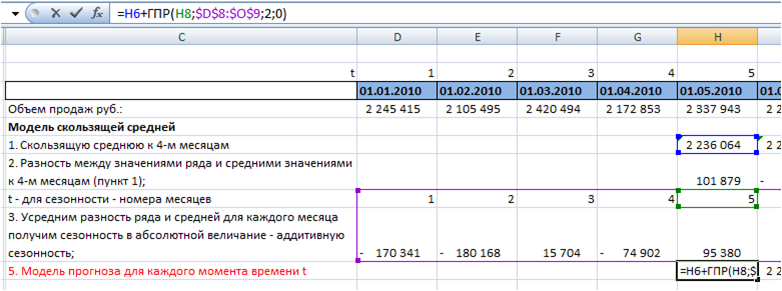
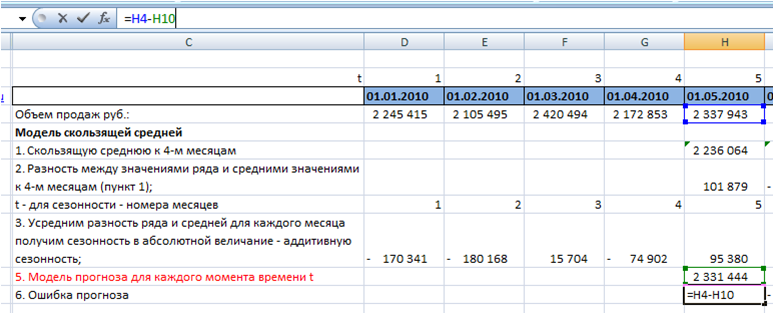
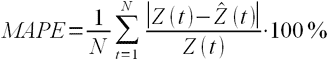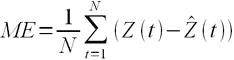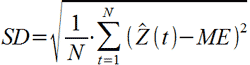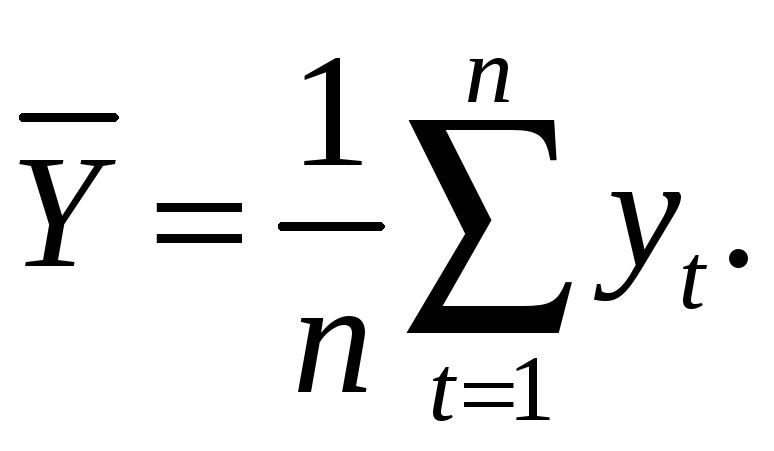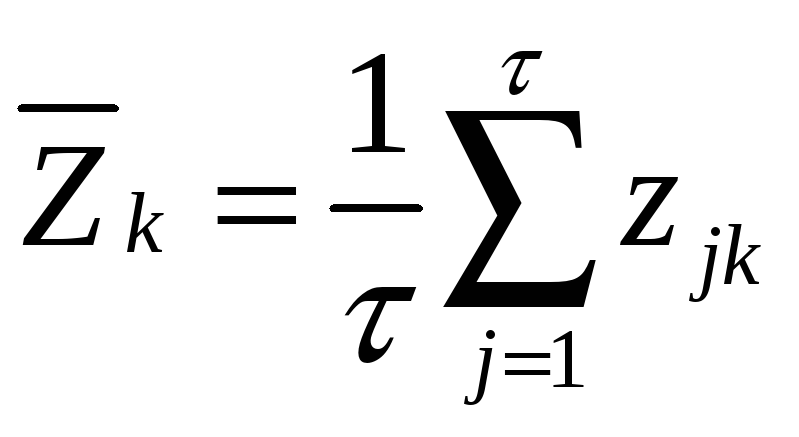Ошибка прогнозирования: виды, формулы, примеры
Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.
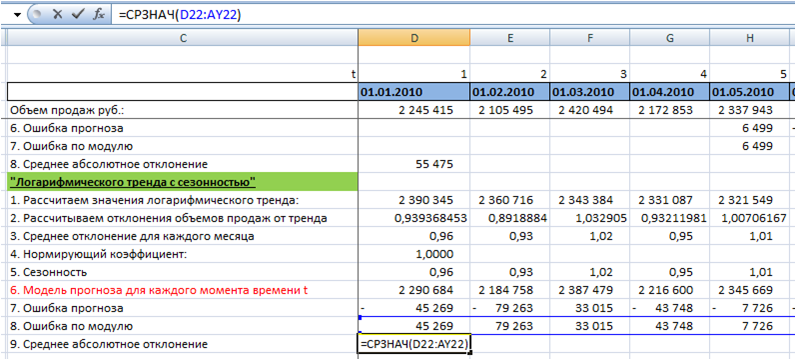
В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):
Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!
MPE — Mean Percent Error
MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.
- Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
- Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
- Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error
MAPE — Mean Absolute Percent Error
MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
- Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
- Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error
Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.
WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error
WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
- Находится сумма всех фактов по всем позициям (общий фактический объем)
- Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE
Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.
Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.
RMSE (as %) / nRMSE — Root Mean Square Error
RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.
- Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
- Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
- Извлекаем корень из полученного результат — RMSE
- Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
- Разделить на разницу между максимальным и минимальным значением показателей
- Разделить на разницу между третьим и первым квартилем значений показателей
- Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)
MASE — Mean Absolute Scaled Error
MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.
Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.
Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:
Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.
Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.
Об авторе
HeinzBr
Автор статей и создатель сайта SHTEM.RU
Ошибка прогнозирования
Поскольку
будущее никогда нельзя в точности
предугадать по прошлому, то прогноз
будущего спроса всегда будет содержать
в себе ошибки в той или иной степени.
Модель экспоненциального сглаживания
прогнозирует средний уровень спроса.
Поэтому следует построить модель так,
чтобы уменьшить разность между прогнозом
и фактическим уровнем спроса. Эта
разность называется ошибкой прогнозирования.
Ошибка
прогнозирования выражается такими
показателями, как среднеквадратическое
отклонение, вариация или среднее
абсолютное отклонение. Раньше среднее
абсолютное отклонение использовалось
в качестве основного измерителя ошибки
прогнозирования при использовании
модели экспоненциального сглаживания.
Среднеквадратическое отклонение
отвергли из-за того, что рассчитывать
его сложнее, чем среднее абсолютное
отклонение, и у компьютеров на это просто
не хватало памяти. Сейчас у компьютеров
достаточно памяти, и теперь
среднеквадратическое отклонение
используется чаще.
Ошибку
прогнозирования можно определить с
помощью следующей формулы:
ОШИБКА
ПРОГНОЗА = ФАКТИЧЕСКИЙ СПРОС – ПРОГНОЗ
СПРОСА
Е
Рис. 3а. Нормальное
распределение ошибок прогноза

прогноз спроса представляет собой
среднее арифметическое фактического
спроса, то сумма ошибок прогнозирования
за определенное количество временных
периодов будет равна нулю. Следовательно,
значение ошибки можно отыскать путем
суммирования квадратов ошибок
прогнозирования, что позволяет избежать
взаимного устранения положительных и
отрицательных ошибок прогнозирования.
Эта сумма делится на количество наблюдений
и затем из нее извлекается квадратный
корень. Показатель корректируется с
уменьшением одной степени свободы,
которая теряется при составлении
прогноза. В результате, уравнение
среднеквадратического отклонения имеет
вид:

г
SE
– средняя ошибка прогнозирования; Ai
– фактический спрос в период i;
Fi
– прогноз на период i;
N
– размер временного ряда.
Ф
Рис. 3б. Скошенное
распределение ошибок прогноза
орма распределения ошибок
прогнозирования является важной, когда
формулируются вероятностные утверждения
о степени надежности прогноза. Две
типовые формы распределения ошибок
прогнозирования показаны на рисунке
3.
Полагая,
что модель прогнозирования отражает
средние значения фактического спроса
достаточно хорошо и отклонения фактических
продаж от прогноза относительно невелики
по сравнению с абсолютной величиной
продаж, то вполне вероятно предположить
нормальное распределение ошибок
прогнозирования. В тех же случаях, когда
ошибка прогнозирования сопоставима по
величине с величиной спроса, имеет место
скошенное, или усеченное нормальное
распределение ошибок прогноза.
Определить
тип распределения в конкретной ситуации
можно с помощью теста на соответствие
критерию согласия хи-квадрат. В качестве
альтернативы можно использовать другой
тест, с помощью которого можно определить,
является ли распределение симметричным
(нормальным) или экспоненциальным
(разновидность скошенного распределения):
При
нормальном распределении около 2%
наблюдаемых значений превышают значение,
равное сумме среднего и удвоенного
значения среднеквадратического
отклонения. При экспоненциальном
распределении около 2% наблюдаемых
значений превышают среднее на величину
среднеквадратического отклонения,
умноженного на коэффициент 2,75.
Следовательно, в первом случае используется
нормальное распределение, а во втором
случае – экспоненциальное.
Пример.
Снова вернемся к нашему примеру. В
базовой модели экспоненциального
сглаживания были получены следующие
результаты:
-
Квартал
I
II
III
IV
Прошлый
год1
200700
900
1
100Текущий
год1
4001
000F3
= ?Прогноз
1
200779
1
005
Оценим
стандартную ошибку прогнозирования по
данным за первый и второй кварталы
текущего года, по которым нам известны
фактические и прогнозные значения.
Допустим, что спрос имеет нормальное
распределение относительно прогноза.
Рассчитаем границы доверительного
интервала с вероятностью 95% для третьего
квартала.
Стандартная
ошибка прогнозирования:
Используя
таблицу А (см. Приложение I), определяем
коэффициент z95%
= 1,96 и получаем границы доверительного
интервала по формуле:
Y
= F3
z(SE)
=1005
1,96298
= 1064
584,2
Следовательно,
с 95%-й вероятностью границы доверительного
интервала прогноза спроса на третий
квартал текущего года составляют
значения:
420,8
< Y
< 1589,2
Основной задачей при управлении запасами является определение объема пополнения, то есть, сколько необходимо заказать поставщику. При расчете этого объема используется несколько параметров — сколько будет продано в будущем, за какое время происходит пополнение, какие остатки у нас на складе и какое количество уже заказано у поставщика. То, насколько правильно мы определим эти параметры, будет влиять на то, будет ли достаточно товара на складе или его будет слишком много. Но наибольшее влияние на эффективность управления запасами влияет то, насколько точен будет прогноз. Многие считают, что это вообще основной вопрос в управлении запасами. Действительно, точность прогнозирования очень важный параметр. Поэтому важно понимать, как его оценивать. Это важно и для выявления причин дефицитов или неликвидов, и при выборе программных продуктов для прогнозирования продаж и управления запасами.
В данной статье я представила несколько формул для расчета точности прогноза и ошибки прогнозирования. Кроме этого, вы сможете скачать файлы с примерами расчетов этого показателя.
Статистические методы
Для оценки прогноза продаж используются статистические оценки Оценка ошибки прогнозирования временного ряда. Самый простой показатель – отклонение факта от прогноза в количественном выражении.
В практике рассчитывают ошибку прогнозирования по каждой отдельной позиции, а также рассчитывают среднюю ошибку прогнозирования. Следующие распространенные показатели ошибки относятся именно к показателям средних ошибок прогнозирования.
К ним относятся:
MAPE – средняя абсолютная ошибка в процентах
где Z(t) – фактическое значение временного ряда, а 
Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.
Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.
MAE – средняя абсолютная ошибка

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.
После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.
Кроме указанных методов иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.
ME – средняя ошибка
Встречается еще другое название этого показателя — Bias (англ. – смещение) демонстрирует величину отклонения, а также — в какую сторону прогноз продаж отклоняется от фактической потребности. Этот индикатор показывает, был ли прогноз оптимистичным или пессимистичным. То есть, отрицательное значение Bias говорит о том, что прогноз был завышен (реальная потребность оказалась ниже), и, наоборот, положительное значение о том, что прогноз был занижен. Цифровое значение показателя определяет величину отклонения (смещения).
MSE – среднеквадратичная ошибка

RMSE – квадратный корень из среднеквадратичной ошибки

.
SD – стандартное отклонение
где ME – есть средняя ошибка, определенная по формуле выше.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме ниже. Скачать пример расчета в Excel >>>
Связь точности и ошибки прогнозирования
В начале этого обсуждения разберемся с определениями.
Ошибка прогноза — апостериорная величина отклонения прогноза от действительного состояния объекта. Если говорить о прогнозе продаж, то это показатель отклонения фактических продаж от прогноза.
Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.
Точность прогноза в % = 100% – MAPE, встречается еще название этого показателя Forecast Accuracy. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности. Показатель точности прогноза выражается в процентах:
- Если точность прогноза равна 100%, то выбранная модель описывает фактические значения на 100%, т.е. очень точно. Нужно сразу оговориться, что такого показателя никогда не будет, основное свойство прогноза в том, что он всегда ошибочен.
- Если 0% или отрицательное число, то совсем не описывает, и данной модели доверять не стоит.
Выбрать подходящую модель прогноза можно с помощью расчета показателя точность прогноза. Модель прогноза, у которой показатель точность прогноза будет ближе к 100%, с большей вероятностью сделает более точный прогноз. Такую модель можно назвать оптимальной для выбранного временного ряда. Говоря о высокой точности, мы говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Не имеет значения, что именно вы будете отслеживать, но важно, чтобы вы сравнивали модели прогнозирования или целевые показатели по одному показателю – ошибка прогноза или точность прогнозирования.
Ранее я использовала оценку MAPE, до тех пор пока не встретила формулу, которую рекомендует Валерий Разгуляев.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>
Оценка ошибки прогноза – формула Валерия Разгуляева (сайт http://upravlenie-zapasami.ru/)
Одной из самых используемых формул оценки ошибки прогнозирования является следующая формула:
где: P – это прогноз, а S – факт за тот же месяц. Однако у этой формулы есть серьезное ограничение — как оценить ошибку, если факт равен нулю? Возможный ответ, что в таком случае D = 100% – который означает, что мы полностью ошиблись. Однако простой пример показывает, что такой ответ — не верен:
|
вариант |
прогноз |
факт |
ошибка прогноза |
|
№1 |
4 |
0 |
100% |
|
№2 |
4 |
1 |
300% |
|
№3 |
1 |
4 |
75% |
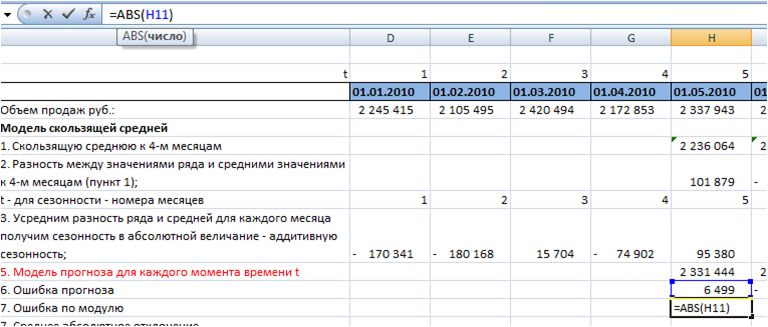
Оказывается, что в варианте развития событий №2, когда мы лучше угадали спрос, чем в варианте №1, ошибка по данной формуле оказалась – больше. То есть ошиблась уже сама формула. Есть и другая проблема, если мы посмотрим на варианты №2 и №3, то увидим, что имеем дело с зеркальной ситуацией в прогнозе и факте, а ошибка при этом отличается – в разы!.. То есть при такой оценке ошибки прогноза нам лучше его заведомо делать менее точным, занижая показатель – тогда ошибка будет меньше!.. Хотя понятно, что чем точнее будет прогноз – тем лучше будет и закупка. Поэтому для расчёта ошибки Валерий Разгуляев рекомендует использовать следующую формулу:
В таком случае для тех же примеров ошибка рассчитается иначе:
|
вариант |
прогноз |
факт |
ошибка прогноза |
|
№1 |
4 |
0 |
100% |
|
№2 |
4 |
1 |
75% |
|
№3 |
1 |
4 |
75% |
Как мы видим, в варианте №1 ошибка становится равной 100%, причём это уже – не наше предположение, а чистый расчёт, который можно доверить машине. Зеркальные же варианты №2 и №3 – имеют и одинаковую ошибку, причём эта ошибка меньше ошибки самого плохого варианта №1. Единственная ситуация, когда данная формула не сможет дать однозначный ответ – это равенство знаменателя нулю. Но максимум из прогноза и факта равен нулю, только когда они оба равны нулю. В таком случае получается, что мы спрогнозировали отсутствие спроса, и его, действительно, не было – то есть ошибка тоже равна нулю – мы сделали совершенно точное предсказание.
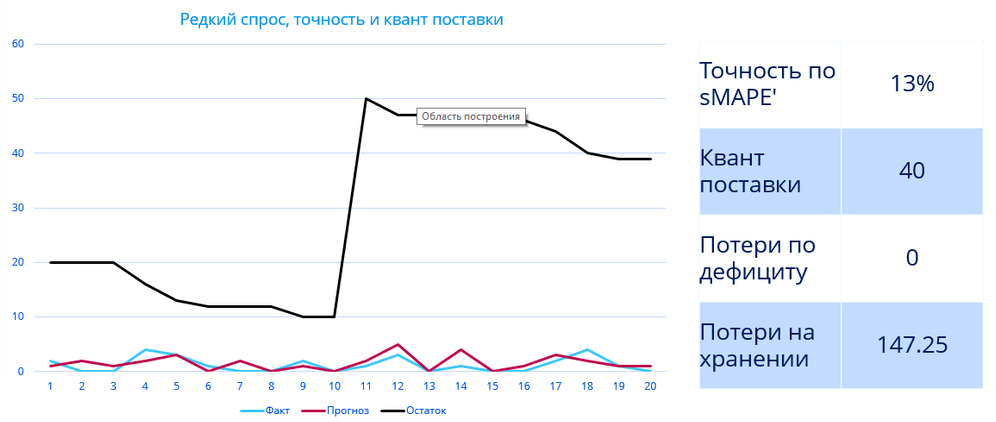
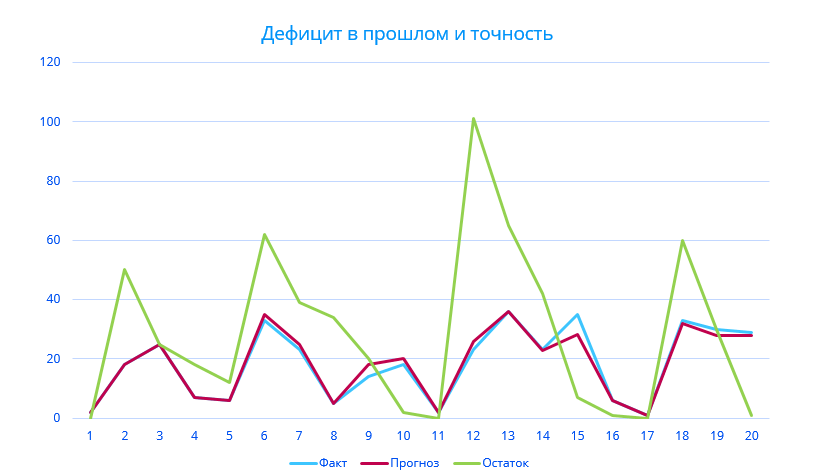
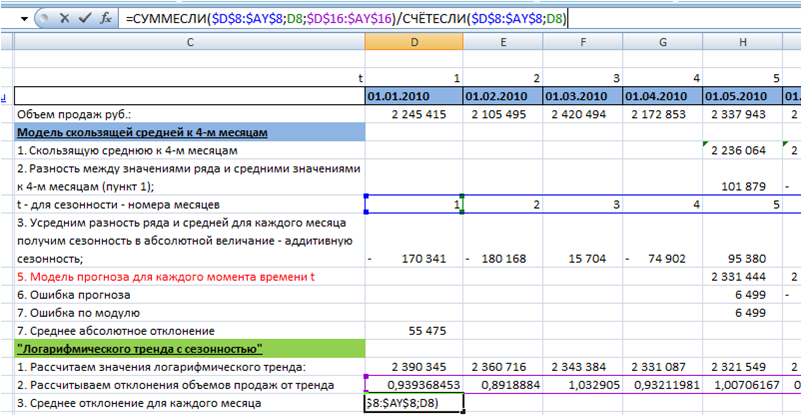
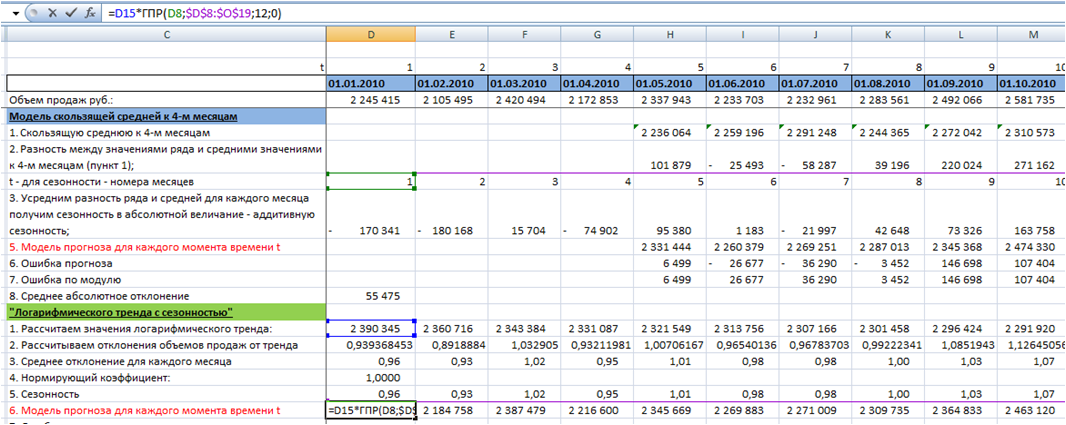
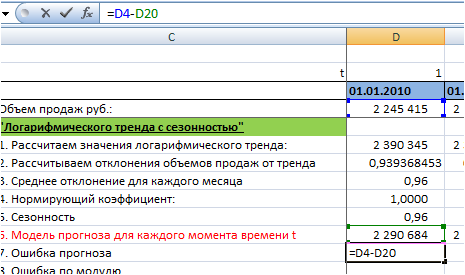
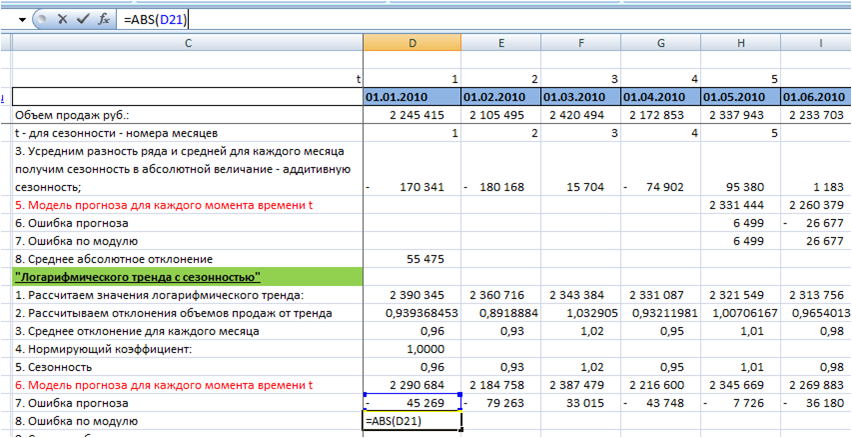
Визуальный метод – графический
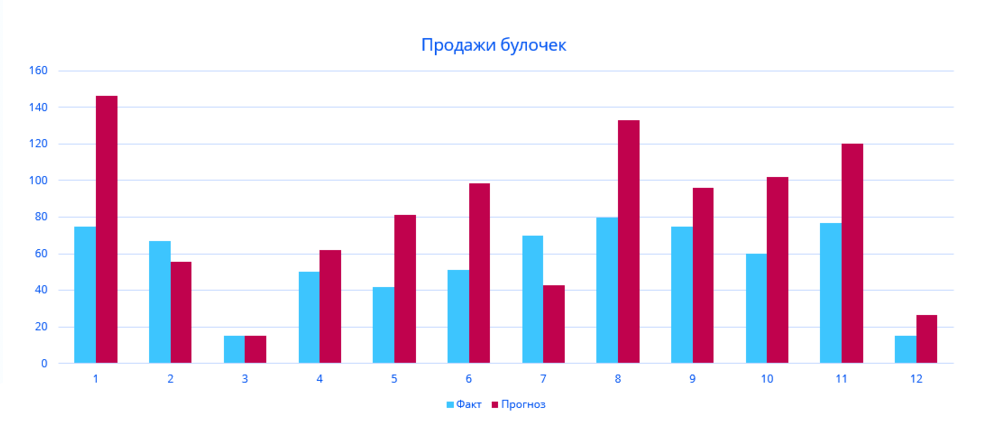
Визуальный метод состоит в том, что мы на график выводим значение прогнозной модели и факта продаж по тем моделям, которые хотим сравнить. Далее сравниваем визуально, насколько прогнозная модель близка к фактическим продажам. Давайте рассмотрим на примере. В таблице представлены две прогнозные модели, а также фактические продажи по этому товару за тот же период. Для наглядности мы также рассчитали ошибку прогнозирования по обеим моделям.
По графикам очевидно, что модель 2 описывает лучше продажи этого товара. Оценка ошибки прогнозирования тоже это показывает – 65% и 31% ошибка прогнозирования по модели 1 и модели 2 соответственно.


Недостатком данного метода является то, что небольшую разницу между моделями сложно выявить — разницу в несколько процентов сложно оценить по диаграмме. Однако эти несколько процентов могут существенно улучшить качество прогнозирования и планирования пополнения запасов в целом.
Использование формул ошибки прогнозирования на практике
Практический аспект оценки ошибки прогнозирования я вывела отдельным пунктом. Это связано с тем, что все статистические методы расчета показателя ошибки прогнозирования рассчитывают то, насколько мы ошиблись в прогнозе в количественных показателях. Давайте теперь обсудим, насколько такой показатель будет полезен в вопросах управления запасами. Дело в том, что основная цель управления запасами — обеспечить продажи, спрос наших клиентов. И, в конечном счете, максимизировать доход и прибыль компании. А эти показатели оцениваются как раз в стоимостном выражении. Таким образом, нам важно при оценке ошибки прогнозирования понимать какой вклад каждая позиция внесла в объем продаж в стоимостном выражении. Когда мы оцениваем ошибку прогнозирования в количественном выражении мы предполагаем, что каждый товар имеет одинаковый вес в общем объеме продаж, но на самом деле это не так – есть очень дорогие товары, есть товары, которые продаются в большом количестве, наша группа А, а есть не очень дорогие товары, есть товары которые вносят небольшой вклад в объем продаж. Другими словами большая ошибка прогнозирования по товарам группы А будет нам «стоить» дороже, чем низкая ошибка прогнозирования по товарам группы С, например. Для того, чтобы наша оценка ошибки прогнозирования была корректной, релевантной целям управления запасами, нам необходимо оценивать ошибку прогнозирования по всем товарам или по отдельной группе не по средними показателями, а средневзвешенными с учетом прогноза и факта в стоимостном выражении.
Пример расчета такой оценки Вы сможете увидеть в файле Excel.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>
При этом нужно помнить, что для оценки ошибки прогнозирования по отдельным позициям мы рассчитываем по количеству, но вот если нам важно понять в целом ошибку прогнозирования по компании, например, для оценки модели, которую используем, то нам нужно рассчитывать не среднюю оценку по всем товарам, а средневзвешенную с учетом стоимостной оценки. Оценку можно брать по ценам себестоимости или ценам продажи, это не играет большой роли, главное, эти же цены (тип цен) использовать при всех расчетах.
Для чего используется ошибка прогнозирования
В первую очередь, оценка ошибки прогнозирования нам необходима для оценки того, насколько мы ошибаемся при планировании продаж, а значит при планировании поставок товаров. Если мы все время прогнозируем продажи значительно больше, чем потом фактически продаем, то вероятнее всего у нас будет излишки товаров, и это невыгодно компании. В случае, когда мы ошибаемся в обратную сторону – прогнозируем продажи меньше чем фактические продажи, с большой вероятностью у нас будут дефициты и компания не дополучит прибыль. В этом случае ошибка прогнозирования служит индикатором качества планирования и качества управления запасами.
Индикатором того, что повышение эффективности возможно за счет улучшения качества прогнозирования. За счет чего можно улучшить качество прогнозирования мы не будем здесь рассматривать, но одним из вариантов является поиск другой модели прогнозирования, изменения параметров расчета, но вот насколько новая модель будет лучше, как раз поможет показатель ошибки прогнозирования или точности прогноза. Сравнение этих показателей по нескольким моделям поможет определить ту модель, которая дает лучше результат.
В идеальном случае, мы можем так подбирать модель для каждой отдельной позиции. В этом случае мы будем рассчитывать прогноз по разным товарам по разным моделям, по тем, которые дают наилучший вариант именно для конкретного товара.
Также этот показатель можно использовать при выборе автоматизированного инструмента для прогнозирования спроса и управления запасами. Вы можете сделать тестовые расчеты прогноза в предлагаемой программе и сравнить ошибку прогнозирования полученного прогноза с той, которая есть у вашей существующей модели. Если у предлагаемого инструмента ошибка прогнозирования меньше. Значит, этот инструмент можно рассматривать для применения в компании. Кроме этого, показатель точности прогноза или ошибки прогнозирования можно использовать как KPI сотрудников, которые отвечают за подготовку прогноза продаж или менеджеров по закупкам, в том случае, если они рассчитывают прогноз будущих продаж при расчете заказа.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>
Если вы хотите повысить эффективность управления запасами и увеличить оборачиваемость товарных запасов, предлагаю изучить мастер-класс «Как увеличить оборачиваемость товарных запасов».
Источник: сайт http://uppravuk.net/
Что такое ошибка прогноза в статистике? (Определение и примеры)
17 авг. 2022 г.
читать 2 мин
В статистике ошибка прогнозирования относится к разнице между прогнозируемыми значениями, сделанными некоторой моделью, и фактическими значениями.
Ошибка прогноза часто используется в двух случаях:
1. Линейная регрессия: используется для прогнозирования значения некоторой переменной непрерывного отклика.
Обычно мы измеряем ошибку прогноза модели линейной регрессии с помощью метрики, известной как RMSE , что означает среднеквадратичную ошибку.
Он рассчитывается как:
СКО = √ Σ(ŷ i – y i ) 2 / n
куда:
- Σ — это символ, который означает «сумма»
- ŷ i — прогнозируемое значение для i -го наблюдения
- y i — наблюдаемое значение для i -го наблюдения
- n — размер выборки
2. Логистическая регрессия: используется для прогнозирования значения некоторой бинарной переменной отклика.
Одним из распространенных способов измерения ошибки прогнозирования модели логистической регрессии является метрика, известная как общий коэффициент ошибочной классификации.
Он рассчитывается как:
Общий коэффициент ошибочной классификации = (# неверных прогнозов / # всего прогнозов)
Чем ниже значение коэффициента ошибочной классификации, тем лучше модель способна предсказать результаты переменной отклика.
В следующих примерах показано, как на практике рассчитать ошибку прогнозирования как для модели линейной регрессии, так и для модели логистической регрессии.
Пример 1: Расчет ошибки прогноза в линейной регрессии
Предположим, мы используем регрессионную модель, чтобы предсказать количество очков, которое 10 игроков наберут в баскетбольном матче.
В следующей таблице показаны прогнозируемые очки по модели и фактические очки, набранные игроками:
Мы рассчитали бы среднеквадратичную ошибку (RMSE) как:
- СКО = √ Σ(ŷ i – y i ) 2 / n
- СКО = √(((14-12) 2 +(15-15) 2 +(18-20) 2 +(19-16) 2 +(25-20) 2 +(18-19) 2 +(12- 16) 2 +(12-20) 2 +(15-16) 2 +(22-16) 2 ) / 10)
- СКО = 4
Среднеквадратическая ошибка равна 4. Это говорит нам о том, что среднее отклонение между прогнозируемыми набранными баллами и фактическими набранными баллами равно 4.
Связанный: Что считается хорошим значением RMSE?
Пример 2: Расчет ошибки прогноза в логистической регрессии
Предположим, мы используем модель логистической регрессии, чтобы предсказать, попадут ли 10 баскетболистов из колледжа в НБА.
В следующей таблице показан прогнозируемый результат для каждого игрока по сравнению с фактическим результатом (1 = выбран на драфте, 0 = не выбран на драфте):
Мы рассчитали бы общий коэффициент ошибочной классификации как:
- Общий коэффициент ошибочной классификации = (# неверных прогнозов / # всего прогнозов)
- Общий коэффициент ошибочной классификации = 4/10
- Общий коэффициент ошибочной классификации = 40%
Общий уровень ошибочной классификации составляет 40% .
Это значение довольно велико, что указывает на то, что модель не очень хорошо предсказывает, будет ли игрок выбран на драфте.
Дополнительные ресурсы
Следующие руководства содержат введение в различные типы методов регрессии:
Введение в простую линейную регрессию
Введение в множественную линейную регрессию
Введение в логистическую регрессию
Для анализа результатов расчета прогноза, в продолжение ряда вы можете рассчитать следующие ошибки:
- MAPE – средняя абсолютная ошибка в % . Ошибка оценивает на сколько велики ошибки в сравнении со значением ряда и с ошибками в соседних рядах.
Подробнее читайте в статье на нашем сайте: http://4analytics.ru/metodi-analiza/mape-%E2%80%93-srednyaya-absolyutnaya-oshibka-praktika-primeneniya.html - MRPE – средняя относительная ошибка в %, оценивает на сколько велика дельта между фактом и прогнозом. Чем ближе к 100%, тем больше ошибка, чем ближе к нулю, тем ошибка меньше.
- MSE – средняя квадратическая ошибка, подчеркивает большие ошибки за счет возведения каждой ошибки в квадрат.
Подробнее читайте в статье на нашем сайте:
http://4analytics.ru/metodi-analiza/mse-%E2%80%93-srednekvadraticheskaya-oshibka-v-excel.html - MPE – средняя процентная ошибка – показывает завышен или занижен прогноз относительно факта. Если ошибка меньше нулю, то прогноз последовательно завышен, если ошибка больше нуля, то прогноз последовательно занижен.
Подробнее читайте в статье на нашем сайте:
http://4analytics.ru/metodi-analiza/mpe-%E2%80%93-srednyaya-procentnaya-oshibka-v-excel.html - MAD – среднее абсолютное отклонение. Используется, когда важно измерить ошибку в тех же единицах, что и исходный ряд.
Подробнее читайте в статье на нашем сайте:
http://4analytics.ru/planirovanie-i-prognozirovanie-praktika/dopolnitelnie-oborotnie-sredstva-za-schet-povisheniya-tochnosti-prognoza.html - A MAPE – ошибка, которая показывает отклонение средних значений ряда к средним значениям модели прогноза. Имеет значение при неравномерном перераспределении значений ряда по периодам.
- S MAPE – ошибка, которая показывает отклонение суммы значения ряда к сумме значений модели прогноза. Имеет значение при неравномерном перераспределении значений ряда по периодам.
А также 2 показателя «Точность прогноза»:
- Точность прогноза = 1 – МАРЕ
- Точность прогноза 2 = 1 – MRPE
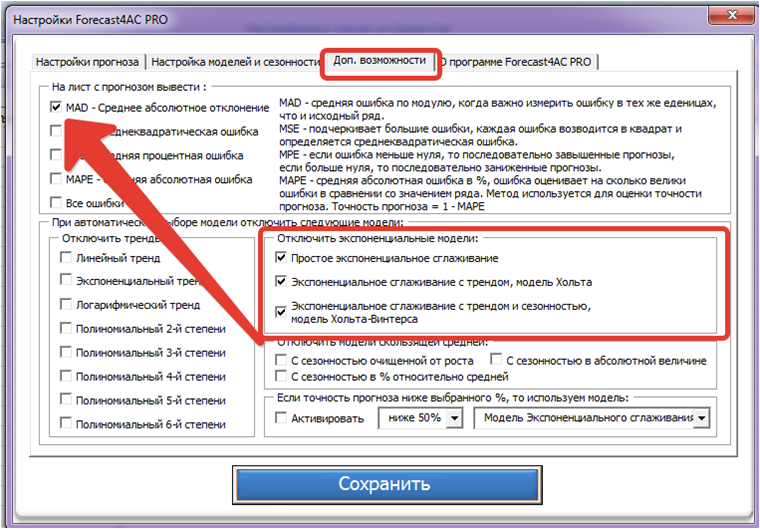
Для расчета ошибок одновременно с прогнозом, нажимаем кнопку «Расчет ошибок» в меню «FORECAST»
В открывшемся окне выбираем нужные для расчета ошибки:
Теперь при расчете прогноза, в продолжение ряда, программа автоматически сделает расчет отмеченных Вами ошибок:
Когда перед компанией встают задачи прогнозирования спроса для управления товарными запасами, обычно появляется вопрос, связанный с выбором метода прогнозирования. Но как определить, какой метод лучше? Однозначного ответа на этот вопрос нет. Однако, исходя из нашей практики, самым распространенным методам оценки точности прогноза является средняя абсолютная процентная ошибка (MAPE). Также используются средняя абсолютная ошибка (MAE) и средняя квадратичная ошибка прогнозирования (RMSE).
Ошибка прогноза в данном случае – это разница между фактическим значением спроса и его прогнозным значением. Т.е, чем больше будет ошибка прогнозирования, тем менее точен прогноз. Например, при ошибке прогнозирования 5%, точность прогноза будет составлять 95%. Изначально MAPE использовалась для прогнозирования временных рядов, которые имеют регулярное нормальное распределение, такие как, например, потребление электроэнергии. И только после ее стали применять для оценки прогноза спроса. На практике ошибку могут рассчитывать по каждой позиции товара, а также среднюю оценку по всем товарным группам.
Несмотря на то, что большинство компаний до сих пор используют вышеописанные методы для оценки, мы считаем, что они не достаточно корректны и не подходят для применения в реальном бизнесе. Для простоты изложения, выделим три ключевых момента, которые приводят к некорректным выводам при использовании вышеописанных методов оценки. Назовем их ошибка №1, №2 и №3. Сначала мы подробно опишем эти ошибки, а потом расскажем, как наши методы сравнения помогаю их ликвидировать.
О некорректности использования MAPE, RMSE и других распространенных ошибок
Ошибка № 1 заключается в том, что используемые методы больше относятся к математике, нежели к бизнесу, по той причине, что это обезличенные цифры (или проценты), которые ничего не говорят про деньги. Бизнесу же нужно принимать решения на основе выгоды, которую он получит в деньгах. Например, ошибка в 80% на первый взгляд звучит устрашающие. Но в реальности за ней могут скрываться совершенно разные вещи. Ошибка по гвоздям со стоимостью одного гвоздя в 0,5 рублей – это одни потери. Но они совершенно несопоставимы с потерями от продажи промышленного оборудования стоимостью 700 000 рублей с той же величиной ошибки прогнозирования. Ко всему прочему также больше значение имеет объем продукции, что тоже никак не учитывается данными ошибками прогнозирования.
Второй важный момент (ошибка №2), который не учитывают данные оценки прогнозирования – это заморозка денежных средств в запасах и недополученная прибыль от дефицита продукции на складе. Например, если мы прогнозируем продажу 20 колесных дисков, а по факту продали 15. То это одна цена ошибки – 5 колесных дисков, которые потребуют затраты на хранение на определенное время, и как следствие стоимость замороженных оборотных средств под определенный процент. Если рассмотреть обратную ситуацию – прогнозируем продажу 20 дисков, спрос составляет 25 штук. Это уже упущенная прибыль, которая составляет разницу сумм закупки и реализации продукции. По сути мы имеет одну и ту же ошибку прогнозирования, но результат от нее может быть совершенно разным.
Третий ключевой момент (ошибка №3) – описанные ошибки распространяются только на точечный прогноз спроса и не описывают страховой запас. А он в некоторых случаях может составлять от 20% до 70% от общих товарных запасов на складе. Поэтому, какой бы точный не был прогноз с точки зрения описанных выше методов, мы все равно не оцениваем точность страхового запаса, а значит реальные данные могут быть значительно искажены.
Критерии, привязанные к прибыльности бизнеса
Учитывая описанные выше недостатки ошибок прогнозирования, такой подход не является корректным и надежным для сравнения алгоритмов. Ко всему прочему он зачастую оторван от реального бизнеса. Используемый же нами подход позволяет оценить точность алгоритмов в деньгах, рассчитать стоимость ошибки прогнозирования на понятном для бизнеса языке финансов. Таким образом это позволяет нам ликвидировать ошибку №1.
В случае с ошибкой № 2, мы рассчитываем два различных значения. Если прогноз окажется меньше реального спроса, то он приведет к дефициту, экономический урон от которого рассчитывается, как количество недопроданных товаров, умноженное на разность цен закупки и реализации. Например, вы закупаете колесные диски по 3000 рублей за штуку и продаете по 4000. Прогноз на месяц составил 1000 дисков, реальный спрос оказался 1200 штук. Экономический урон будет равен:
(1200-1000)*(4000-3000)=200 000 рублей.
В случае превышения прогноза над реальным спросом компания понесет убытки по хранению продукции. Экономический урон будет равен сумме затрат на нереализованную продукцию, помноженную на ставку альтернативных вложений за этот период. Предположим, что реальный спрос в предыдущем примере оказался 800 дисков и вам пришлось хранить диски еще один месяц. Пусть ставка альтернативных вложений составляет 20% в год. Тогда экономический урон будет равен
(1000-800)*3000*0,2/12=10 000 рублей.
Соответственно, в каждом конкретном случае, мы будет учитывать одно из этих значений.
Для того, чтобы ликвидировать ошибку № 3, мы сравниваем алгоритмы с использованием понятия уровень сервиса. Уровень сервиса (здесь и далее — уровень сервиса II рода, fill rate) – это доля спроса, которую мы гарантировано покроем с использованием имеющихся на складе запасов в течении периода их пополнения. Например, уровень сервиса 90% означает, что мы удовлетворим 90% спроса. На первый взгляд может показаться логичным, что уровень сервиса всегда должен составлять 100%. Тогда и прибыль будет максимальна. Но в реальных ситуациях зачастую дело обстоит иначе: удовлетворение 100% уровня сервиса приводит к сильному перезатариванию склада, а для товаров с ограниченными сроками годности еще и к списанию. И убытки от затрат на хранение, списания просроченной продукции и недополученной прибыли от вложения свободных денег в итоге снизят прибыть от реализации, в случае если бы мы поддерживали уровень сервиса 95%. Нужно заметить, что для каждой отдельной позиции товаров будет свой оптимальный уровень сервиса.
Подробнее о уровне сервиса, его видах и примерах расчета читайте в статье «Что такое уровень сервиса и почему он важен.»
Так как страховой запас может составлять значительную долю, его нельзя игнорировать при сравнении алгоритмов (как это делается при расчете ошибок MAPE, RMSE и т.д.). Поэтому мы делаем сравнение не прогноза, а оптимального запаса с заданным уровнем сервиса. Оптимальный запас для заданного уровня сервиса – это такое количество товаров, которое нужно хранить на складе, чтобы получить максимум прибыли от реализации товаров и одновременно сократить издержки на хранение до минимума.
В качестве основного критерия (критерий №1) качества прогнозирования мы используем суммарное значение потерь для заданного уровня сервиса, о котором писали выше (исправление ошибки №2). Таким образом мы оцениваем потери в денежном выражении при использовании данного конкретного алгоритма. Чем меньше потери — тем точнее работает алгоритм.
Здесь нужно заметить, что для разных уровней сервиса оптимальный запас тоже может различаться. И в одном случае прогноз будет точно в него попадать, а в другом возможны перекосы в большую, либо меньшую сторону. Так как многие компании не рассчитывают оптимальный уровень сервиса, а используют заданный заранее, значение основного критерия мы вычисляем для всех самых распространенных уровней сервиса: 70%, 75%, 80%, 85%, 90%, 95%, 98%, 99% и суммируем потери. Таким образом мы можем проверить, насколько хорошо в целом работает модель.
Для компаний, которые, считают оптимальный уровень сервиса мы используем дополнительный критерий (критерий №2) для оценки. В общем виде он выглядит как соотношение потерь на оптимальном уровне сервиса по ожидаемому (модельному) распределению продаж и по реальному распределению продаж (по факту). Прогнозируемое значение оптимального уровня сервиса не всегда соответствует оптимальному значению уже на реальном распределении продаж. Поэтому мы должны сравнивать ошибку между прогнозом объема продаж на оптимальном (по модели) уровне сервиса и реальным объемом продаж, обеспечивающим оптимальное значение уровня сервиса по реальным данным.
Что проиллюстрировать применение данного критерия, вернемся к нашему примеру с дисками. Предположим, что прогнозное значение оптимального уровня сервиса для него составляет 90%, а оптимальный объем запаса для этого случая примем равным 3000 колесных дисков. Пусть в первом случае реальный уровень сервиса оказался выше прогнозного и составил 92%. Соответственно объем заказов также вырос и составил 3300 дисков. Ошибка прогнозирования будет рассчитываться как разность между реальным и фактическим объемом продаж, умноженная на разность цен реализации. Итого, мы имеем:
(3300-3000)*(4000-3000)=300 000 рублей.
Теперь представим обратную ситуацию: реальный уровень сервиса оказался меньше прогнозного и составил 87%. Реальный объем продаж при этом составил 2850 дисков. Ошибка прогнозирования будет рассчитана, как сумма затрат на нереализованную продукцию, умноженную на ставку альтернативных вложений за этот период (в качестве примера берем период сроком месяц и ставку равную 20% годовых). Итоговое значение критерия будет равно:
(3000-2850)*3000*0,2/12 = 7500 рублей
Конечно, в идеальном случае, мы должны рассчитывать ошибку только при оптимальном уровне сервиса, между прогнозным и реальным значениями. Но так как не все компании еще перешли на оптимальный уровень сервиса, мы вынуждены использовать два критерия.
Используемые нами критерии в отличие от классических математических ошибок, показывают суммарные потери в деньгах при применении той или иной модели. Соответственно, наилучшей будет модель, которая обеспечивает минимальные потери. Такой подход позволят бизнес-пользователям оценить работу различных алгоритмов на понятном им языке.
Пример сравнения точности прогнозирования системы Forecast NOW c методом ARIMA (на базе номенклатуры бытовой химии):
|
Критерий (потери в рублях) |
Forecast NOW! |
ARIMA |
Разность |
|
Критерий №1 (потери на оптимальном уровне сервиса) |
92 997 114 |
169 916 601 |
82,71% |
|
Критерий №2 |
4 188 749 |
7 611 365 |
81,71% |
|
Критерий №1 (суммарное значение по распространенным уровням сервиса) |
820 099 299 |
1 550 434 475 |
89,05% |
Пример сравнения точности прогнозирования системы Forecast NOW c методом Кростона (на базе номенклатуры бытовой химии):
|
Критерий (потери в рублях) |
Forecast NOW! |
Метод Кростона |
Разность |
|
Критерий №1 (потери на оптимальном уровне сервиса) |
6 379 616 |
8 328 509 |
30,55% |
|
Критерий №2 |
1 076 984 |
1 341 537 |
24,56% |
|
Критерий №1 (суммарное значение по распространенным уровням сервиса) |
128 690 989 |
161 891 666 |
20,51% |
Оценка ошибки прогнозирования временного ряда
Работая с научными публикациями, сталкиваюсь с различными показателями ошибок прогнозирования временных рядов. Среди всех встречающихся оценок ошибки прогнозирования стоит отметить две, которые в настоящее время, являются самыми популярными: MAE и MAPE.
Пусть ошибка есть разность:
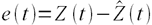
где Z(t) – фактическое значение временного ряда, а 
Тогда формулы для оценок ошибки прогнозирования временных рядов для N отчетов можно записать в следующем виде.
MAPE – средняя абсолютная ошибка в процентах
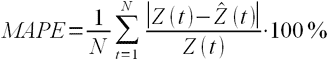
Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.
Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.
MAE – средняя абсолютная ошибка

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.
После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.
Кроме указанных иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.
MSE – среднеквадратичная ошибка

RMSE – квадратный корень из среднеквадратичной ошибки

ME – средняя ошибка
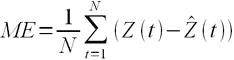
SD – стандартное отклонение
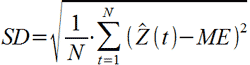
Связь точности и ошибки прогнозирования
Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.
Точность прогноза в % = 100% – MAPE
Величину точности оценивать не принято, говоря о прогнозировании всегда оценивают, то есть определяют значение именно ошибки прогноза, то есть величину MAPE и/или MAE. Однако нужно понимать, что если MAPE = 5%, то точность прогнозирования = 95%. Говоря о высокой точности, мы всегда говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности.
При этом величина MAPE является количественной оценкой именно ошибки, и эта величина нам ясно говорит и о точности прогнозирования, исходя из приведенной выше простой формулы. Таким образом, оценивая ошибку, мы всегда оцениваем точность прогнозирования.
Перевод
Ссылка на автора
Показатели эффективности прогнозирования по временным рядам дают сводку об умениях и возможностях модели прогноза, которая сделала прогнозы.
Есть много разных показателей производительности на выбор. Может быть непонятно, какую меру использовать и как интерпретировать результаты.
В этом руководстве вы узнаете показатели производительности для оценки прогнозов временных рядов с помощью Python.
Временные ряды, как правило, фокусируются на прогнозировании реальных значений, называемых проблемами регрессии. Поэтому показатели эффективности в этом руководстве будут сосредоточены на методах оценки реальных прогнозов.
После завершения этого урока вы узнаете:
- Основные показатели выполнения прогноза, включая остаточную ошибку прогноза и смещение прогноза.
- Вычисления ошибок прогноза временного ряда, которые имеют те же единицы, что и ожидаемые результаты, такие как средняя абсолютная ошибка.
- Широко используются вычисления ошибок, которые наказывают большие ошибки, такие как среднеквадратическая ошибка и среднеквадратичная ошибка.
Давайте начнем.
Ошибка прогноза (или остаточная ошибка прогноза)
ошибка прогноза рассчитывается как ожидаемое значение минус прогнозируемое значение.
Это называется остаточной ошибкой прогноза.
forecast_error = expected_value - predicted_valueОшибка прогноза может быть рассчитана для каждого прогноза, предоставляя временной ряд ошибок прогноза.
В приведенном ниже примере показано, как можно рассчитать ошибку прогноза для серии из 5 прогнозов по сравнению с 5 ожидаемыми значениями. Пример был придуман для демонстрационных целей.
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
forecast_errors = [expected[i]-predictions[i] for i in range(len(expected))]
print('Forecast Errors: %s' % forecast_errors)При выполнении примера вычисляется ошибка прогноза для каждого из 5 прогнозов. Список ошибок прогноза затем печатается.
Forecast Errors: [-0.2, 0.09999999999999998, -0.1, -0.09999999999999998, -0.2]Единицы ошибки прогноза совпадают с единицами прогноза. Ошибка прогноза, равная нулю, означает отсутствие ошибки или совершенный навык для этого прогноза.
Средняя ошибка прогноза (или ошибка прогноза)
Средняя ошибка прогноза рассчитывается как среднее значение ошибки прогноза.
mean_forecast_error = mean(forecast_error)Ошибки прогноза могут быть положительными и отрицательными. Это означает, что при вычислении среднего из этих значений идеальная средняя ошибка прогноза будет равна нулю.
Среднее значение ошибки прогноза, отличное от нуля, указывает на склонность модели к превышению прогноза (положительная ошибка) или занижению прогноза (отрицательная ошибка). Таким образом, средняя ошибка прогноза также называется прогноз смещения,
Ошибка прогноза может быть рассчитана непосредственно как среднее значение прогноза. В приведенном ниже примере показано, как среднее значение ошибок прогноза может быть рассчитано вручную.
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
forecast_errors = [expected[i]-predictions[i] for i in range(len(expected))]
bias = sum(forecast_errors) * 1.0/len(expected)
print('Bias: %f' % bias)При выполнении примера выводится средняя ошибка прогноза, также известная как смещение прогноза.
Bias: -0.100000Единицы смещения прогноза совпадают с единицами прогнозов. Прогнозируемое смещение нуля или очень маленькое число около нуля показывает несмещенную модель.
Средняя абсолютная ошибка
средняя абсолютная ошибка или MAE, рассчитывается как среднее значение ошибок прогноза, где все значения прогноза вынуждены быть положительными.
Заставить ценности быть положительными называется сделать их абсолютными. Это обозначено абсолютной функциейабс ()или математически показано как два символа канала вокруг значения:| Значение |,
mean_absolute_error = mean( abs(forecast_error) )кудаабс ()делает ценности позитивными,forecast_errorодна или последовательность ошибок прогноза, иимею в виду()рассчитывает среднее значение.
Мы можем использовать mean_absolute_error () функция из библиотеки scikit-learn для вычисления средней абсолютной ошибки для списка прогнозов. Пример ниже демонстрирует эту функцию.
from sklearn.metrics import mean_absolute_error
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
mae = mean_absolute_error(expected, predictions)
print('MAE: %f' % mae)При выполнении примера вычисляется и выводится средняя абсолютная ошибка для списка из 5 ожидаемых и прогнозируемых значений.
MAE: 0.140000Эти значения ошибок приведены в исходных единицах прогнозируемых значений. Средняя абсолютная ошибка, равная нулю, означает отсутствие ошибки.
Средняя квадратическая ошибка
средняя квадратическая ошибка или MSE, рассчитывается как среднее значение квадратов ошибок прогноза. Возведение в квадрат значений ошибки прогноза заставляет их быть положительными; это также приводит к большему количеству ошибок.
Квадратные ошибки прогноза с очень большими или выбросами возводятся в квадрат, что, в свою очередь, приводит к вытягиванию среднего значения квадратов ошибок прогноза, что приводит к увеличению среднего квадрата ошибки. По сути, оценка дает худшую производительность тем моделям, которые делают большие неверные прогнозы.
mean_squared_error = mean(forecast_error^2)Мы можем использовать mean_squared_error () функция из scikit-learn для вычисления среднеквадратичной ошибки для списка прогнозов. Пример ниже демонстрирует эту функцию.
from sklearn.metrics import mean_squared_error
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
mse = mean_squared_error(expected, predictions)
print('MSE: %f' % mse)При выполнении примера вычисляется и выводится среднеквадратическая ошибка для списка ожидаемых и прогнозируемых значений.
MSE: 0.022000Значения ошибок приведены в квадратах от предсказанных значений. Среднеквадратичная ошибка, равная нулю, указывает на совершенное умение или на отсутствие ошибки.
Среднеквадратическая ошибка
Средняя квадратичная ошибка, описанная выше, выражается в квадратах единиц прогнозов.
Его можно преобразовать обратно в исходные единицы прогнозов, взяв квадратный корень из среднего квадрата ошибки Это называется среднеквадратичная ошибка или RMSE.
rmse = sqrt(mean_squared_error)Это можно рассчитать с помощьюSQRT ()математическая функция среднего квадрата ошибки, рассчитанная с использованиемmean_squared_error ()функция scikit-learn.
from sklearn.metrics import mean_squared_error
from math import sqrt
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
mse = mean_squared_error(expected, predictions)
rmse = sqrt(mse)
print('RMSE: %f' % rmse)При выполнении примера вычисляется среднеквадратичная ошибка.
RMSE: 0.148324Значения ошибок RMES приведены в тех же единицах, что и прогнозы. Как и в случае среднеквадратичной ошибки, среднеквадратическое отклонение, равное нулю, означает отсутствие ошибки.
Дальнейшее чтение
Ниже приведены некоторые ссылки для дальнейшего изучения показателей ошибки прогноза временных рядов.
- Раздел 3.3 Измерение прогнозирующей точности, Практическое прогнозирование временных рядов с помощью R: практическое руководство,
- Раздел 2.5 Оценка точности прогноза, Прогнозирование: принципы и практика
- scikit-Learn Metrics API
- Раздел 3.3.4. Метрики регрессии, scikit-learn API Guide
Резюме
В этом руководстве вы обнаружили набор из 5 стандартных показателей производительности временных рядов в Python.
В частности, вы узнали:
- Как рассчитать остаточную ошибку прогноза и как оценить смещение в списке прогнозов.
- Как рассчитать среднюю абсолютную ошибку прогноза, чтобы описать ошибку в тех же единицах, что и прогнозы.
- Как рассчитать широко используемые среднеквадратические ошибки и среднеквадратичные ошибки для прогнозов.
Есть ли у вас какие-либо вопросы о показателях эффективности прогнозирования временных рядов или об этом руководстве?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.
Когда перед компанией встают задачи прогнозирования спроса для управления товарными запасами, обычно появляется вопрос, связанный с выбором метода прогнозирования. Но как определить, какой метод лучше?
Однозначного ответа на этот вопрос нет. Однако, исходя из нашей практики, самым распространенным методам оценки точности прогноза является средняя абсолютная процентная ошибка (MAPE) . Также используются средняя абсолютная ошибка (MAE) и средняя квадратичная ошибка прогнозирования (RMSE).
Ошибка прогноза в данном случае – это разница между фактическим значением спроса и его прогнозным значением. Т. е, чем больше будет ошибка прогнозирования, тем менее точен прогноз. Например, при ошибке прогнозирования 5%, точность прогноза будет составлять 95%. Изначально MAPE использовалась для прогнозирования временных рядов, которые имеют регулярное нормальное распределение, такие как, например, потребление электроэнергии. И только после ее стали применять для оценки прогноза спроса. На практике ошибку могут рассчитывать по каждой позиции товара, а также среднюю оценку по всем товарным группам.
Несмотря на то, что большинство компаний до сих пор используют вышеописанные методы для оценки, мы считаем, что они не достаточно корректны и не подходят для применения в реальном бизнесе. Для простоты изложения, выделим три ключевых момента, которые приводят к некорректным выводам при использовании вышеописанных методов оценки. Назовем их ошибка № 1, № 2 и № 3. Сначала мы подробно опишем эти ошибки, а потом расскажем, как наши методы сравнения помогаю их ликвидировать.
О некорректности использования MAPE, RMSE и других распространенных ошибок
Ошибка № 1 заключается в том, что используемые методы больше относятся к математике, нежели к бизнесу, по той причине, что это обезличенные цифры (или проценты) , которые ничего не говорят про деньги. Бизнесу же нужно принимать решения на основе выгоды, которую он получит в деньгах. Например, ошибка в 80% на первый взгляд звучит устрашающие. Но в реальности за ней могут скрываться совершенно разные вещи. Ошибка по гвоздям со стоимостью одного гвоздя в 0,5 рублей – это одни потери. Но они совершенно несопоставимы с потерями от продажи промышленного оборудования стоимостью 700 000 рублей с той же величиной ошибки прогнозирования. Ко всему прочему также больше значение имеет объем продукции, что тоже никак не учитывается данными ошибками прогнозирования.
Второй важный момент (ошибка №2), который не учитывают данные оценки прогнозирования – это заморозка денежных средств в запасах и недополученная прибыль от дефицита продукции на складе. Например, если мы прогнозируем продажу 20 колесных дисков, а по факту продали 15. То это одна цена ошибки – 5 колесных дисков, которые потребуют затраты на хранение на определенное время, и как следствие стоимость замороженных оборотных средств под определенный процент. Если рассмотреть обратную ситуацию – прогнозируем продажу 20 дисков, спрос составляет 25 штук. Это уже упущенная прибыль, которая составляет разницу сумм закупки и реализации продукции. По сути мы имеет одну и ту же ошибку прогнозирования, но результат от нее может быть совершенно разным.
Третий ключевой момент (ошибка №3) – описанные ошибки распространяются только на точечный прогноз спроса и не описывают страховой запас. А он в некоторых случаях может составлять от 20% до 70% от общих товарных запасов на складе. Поэтому, какой бы точный не был прогноз с точки зрения описанных выше методов, мы все равно не оцениваем точность страхового запаса, а значит реальные данные могут быть значительно искажены.
Критерии, привязанные к прибыльности бизнеса
Учитывая описанные выше недостатки ошибок прогнозирования, такой подход не является корректным и надежным для сравнения алгоритмов. Ко всему прочему он зачастую оторван от реального бизнеса. Используемый же нами подход позволяет оценить точность алгоритмов в деньгах, рассчитать стоимость ошибки прогнозирования на понятном для бизнеса языке финансов. Таким образом это позволяет нам ликвидировать ошибку №1.
В случае с ошибкой № 2, мы рассчитываем два различных значения. Если прогноз окажется меньше реального спроса, то он приведет к дефициту, экономический урон от которого рассчитывается, как количество недопроданных товаров, умноженное на разность цен закупки и реализации. Например, вы закупаете колесные диски по 3000 рублей за штуку и продаете по 4000. Прогноз на месяц составил 1000 дисков, реальный спрос оказался 1200 штук. Экономический урон будет равен:
(1200-1000)*(4000-3000)=200 000 рублей.
В случае превышения прогноза над реальным спросом компания понесет убытки по хранению продукции. Экономический урон будет равен сумме затрат на нереализованную продукцию, помноженную на ставку альтернативных вложений за этот период. Предположим, что реальный спрос в предыдущем примере оказался 800 дисков и вам пришлось хранить диски еще один месяц. Пусть ставка альтернативных вложений составляет 20% в год. Тогда экономический урон будет равен
(1000-800)*3000*0,2/12=10 000 рублей.
Соответственно, в каждом конкретном случае, мы будет учитывать одно из этих значений.
Для того, чтобы ликвидировать ошибку № 3, мы сравниваем алгоритмы с использованием понятия уровень сервиса. Уровень сервиса (здесь и далее — уровень сервиса II рода, fill rate) – это доля спроса, которую мы гарантировано покроем с использованием имеющихся на складе запасов в течении периода их пополнения. Например, уровень сервиса 90% означает, что мы удовлетворим 90% спроса. На первый взгляд может показаться логичным, что уровень сервиса всегда должен составлять 100%. Тогда и прибыль будет максимальна. Но в реальных ситуациях зачастую дело обстоит иначе: удовлетворение 100% уровня сервиса приводит к сильному перезатариванию склада, а для товаров с ограниченными сроками годности еще и к списанию. И убытки от затрат на хранение, списания просроченной продукции и недополученной прибыли от вложения свободных денег в итоге снизят прибыть от реализации, в случае если бы мы поддерживали уровень сервиса 95%. Нужно заметить, что для каждой отдельной позиции товаров будет свой оптимальный уровень сервиса.
Так как страховой запас может составлять значительную долю, его нельзя игнорировать при сравнении алгоритмов (как это делается при расчете ошибок MAPE, RMSE и т. д.) . Поэтому мы делаем сравнение не прогноза, а оптимального запаса с заданным уровнем сервиса. Оптимальный запас для заданного уровня сервиса – это такое количество товаров, которое нужно хранить на складе, чтобы получить максимум прибыли от реализации товаров и одновременно сократить издержки на хранение до минимума.
В качестве основного критерия (критерий №1) качества прогнозирования мы используем суммарное значение потерь для заданного уровня сервиса, о котором писали выше (исправление ошибки №2). Таким образом мы оцениваем потери в денежном выражении при использовании данного конкретного алгоритма. Чем меньше потери — тем точнее работает алгоритм.
Здесь нужно заметить, что для разных уровней сервиса оптимальный запас тоже может различаться. И в одном случае прогноз будет точно в него попадать, а в другом возможны перекосы в большую, либо меньшую сторону. Так как многие компании не рассчитывают оптимальный уровень сервиса, а используют заданный заранее, значение основного критерия мы вычисляем для всех самых распространенных уровней сервиса: 70%, 75%, 80%, 85%, 90%, 95%, 98%, 99% и суммируем потери. Таким образом мы можем проверить, насколько хорошо в целом работает модель.
Для компаний, которые, считают оптимальный уровень сервиса мы используем дополнительный критерий (критерий №2) для оценки. В общем виде он выглядит как соотношение потерь на оптимальном уровне сервиса по ожидаемому (модельному) распределению продаж и по реальному распределению продаж (по факту) . Прогнозируемое значение оптимального уровня сервиса не всегда соответствует оптимальному значению уже на реальном распределении продаж. Поэтому мы должны сравнивать ошибку между прогнозом объема продаж на оптимальном (по модели) уровне сервиса и реальным объемом продаж, обеспечивающим оптимальное значение уровня сервиса по реальным данным.
Что проиллюстрировать применение данного критерия, вернемся к нашему примеру с дисками. Предположим, что прогнозное значение оптимального уровня сервиса для него составляет 90%, а оптимальный объем запаса для этого случая примем равным 3000 колесных дисков. Пусть в первом случае реальный уровень сервиса оказался выше прогнозного и составил 92%. Соответственно объем заказов также вырос и составил 3300 дисков. Ошибка прогнозирования будет рассчитываться как разность между реальным и фактическим объемом продаж, умноженная на разность цен реализации. Итого, мы имеем:
(3300-3000)*(4000-3000)=300 000 рублей.
Теперь представим обратную ситуацию: реальный уровень сервиса оказался меньше прогнозного и составил 87%. Реальный объем продаж при этом составил 2850 дисков. Ошибка прогнозирования будет рассчитана, как сумма затрат на нереализованную продукцию, умноженную на ставку альтернативных вложений за этот период (в качестве примера берем период сроком месяц и ставку равную 20% годовых) . Итоговое значение критерия будет равно:
(3000-2850)*3000*0,2/12 = 7500 рублей
Конечно, в идеальном случае, мы должны рассчитывать ошибку только при оптимальном уровне сервиса, между прогнозным и реальным значениями. Но так как не все компании еще перешли на оптимальный уровень сервиса, мы вынуждены использовать два критерия.
Используемые нами критерии в отличие от классических математических ошибок, показывают суммарные потери в деньгах при применении той или иной модели. Соответственно, наилучшей будет модель, которая обеспечивает минимальные потери. Такой подход позволят бизнес-пользователям оценить работу различных алгоритмов на понятном им языке.
Пример сравнения точности прогнозирования системы Forecast NOW c методом ARIMA (на базе номенклатуры бытовой химии) :
Пример сравнения точности прогнозирования системы Forecast NOW c методом Кростона (на базе номенклатуры бытовой химии) :
Насколько корректно на ваш взгляд считать ошибки, а не деньги? Предлагаем порассуждать на эту тему в комментариях!
Все методы
прогнозирования базируются на информации
об объекте прогнозирования и его прошлом
развитии. Прогноз, получающийся в
результате применения методов
прогнозирования, определяет ожидаемые
варианты экономического развития. При
этом предполагается, что основные
факторы и тенденции прошлого периода
сохранятся на период прогноза или что
можно обосновать и учесть направление
их изменений в рассматриваемой
перспективе. Такую гипотезу выдвигают
исходя из инерционности развития
социально-экономических явлений и
процессов. Инерционность проявляется
во взаимосвязях, т. e.
сохраняются зависимости, корреляции
прогнозируемой переменной от совокупности
факторных признаков, темпы и направление
развития, вариация показателей на
протяжении длительного периода времени.
Инерционность развития экономики
связана с длительно действующими
факторами (структура основных фондов,
их возраст и эффективность, степень
устойчивости технологических взаимосвязей
отраслей производства и др.).
Для того чтобы
в прогнозе содержалось не только
правильное качественное предсказание,
но и наиболее вероятное количественное
значение прогнозируемого признака,
необходимо, чтобы прогностическая
модель допускала малую ошибку прогноза.
Ошибка прогноза будет тем меньше, чем
меньше срок упреждения и чем длиннее
прошлый период, на информации из которого
построена прогностическая модель, т.
e.
чем длиннее база прогноза. Нет общих
правил определения допустимого срока
упреждения при заданной точности
прогноза, и наоборот: нельзя указать
точность прогноза в зависимости от
срока упреждения. В большинстве случаев
срок упреждения не должен превышать
третьей части длины базы прогноза.
Например, для прогноза на 5 лет желательно,
чтобы база прогноза (ряд динамики)
содержала не менее 15 уровней. В каждом
конкретном случае соотношение длины
базы прогноза и срока упреждения
необходимо обосновывать, используя
имеющуюся информацию.
При прогнозировании
нужно взвешивать все существующие
методы, чтобы воспользоваться тем из
них, который наиболее полно отвечает
данным обстоятельствам. Прежде всего,
следует рассмотреть метод, в котором
исследуемый динамический ряд
экстраполируется. При этом тренд,
краткосрочную осцилляцию, сезонный
эффект объединяют сложением или
умножением, в зависимости от обстоятельств,
с тем чтобы сформировать прогноз. Затем
исследуют ошибки прогноза, т. e.
вычисляют стандартную ошибку оценки
или доверительный интервал оценки,
выражая на языке вероятностей степень
уверенности в том, что оценка лежит в
заданной области. Все эти действия
основываются на том, что исследуемая
выборка извлечена случайным образом
из генеральной совокупности. При
прогнозировании, осуществляя разложение
(на тренд, краткосрочную осцилляцию,
сезонную и случайную компоненты), строят
модель. Ошибки прогноза проявляются и
вследствие ошибок спецификации этой
модели.
Наиболее точный
способ оценивания надежности метода
прогноза состоит в исследовании его
“работы” за какой-либо период. По ряду
рассчитанных ошибок можно сформировать
хорошую эмпирическую оценку ошибки,
которая, вероятно, встретится в будущем.
Однако такой метод оценки надежности
требует большего труда. Разумным
компромиссом оказывается вычисление
ошибок для прошлых моментов времени на
основе текущих значений. Это может
привести к недооценке истинных ошибок,
но, по крайней мере, будет получено
некоторое представление об ошибках в
будущем.
Число единиц
времени, на которое делается прогноз,
называется горизонтом
прогнозирования.
Рассмотрим
теперь наиболее распространенные методы
прогнозирования экономических явлений
и процессов, называемые адаптивными,
так как при получении новой информации
о динамических рядах производится
корректировка параметров моделирования,
т. e.
их адаптация к новым непрерывно
изменяющимся условиям.
9.1. Прогнозирование
с использованием показателей средних
характеристик ряда динамики.
Одним из наиболее распространенных
методов краткосрочного прогнозирования
социально-экономических явлений и
процессов является экстраполяция, т.
e.
распространение прошлых и настоящих
закономерностей, связей, соотношений
на будущее. Наиболее простым методом
экстраполяции одномерных рядов динамики
является использование средних
характеристик: среднего
уровня, среднего абсолютного прироста
и среднего темпа роста.
При использовании
среднего уровня ряда динамики в
прогнозировании социально-экономических
явлений прогнозируемый уровень
принимается равным среднему значению
уровней ряда в прошлом:
,
Прогноз вычисляется
на
моментов времени вперед (период
упреждения), т. e.
до момента
(горизонт прогнозирования). Получается
прогностическая точечная оценка,
которая, вообще говоря, не совпадает с
фактическими данными. Поэтому для
средней указывается доверительный
интервал прогноза
,
где
табличное
значение
-критерия
Стьюдента с
= n
— 1 степенями свободы и уровнем доверия
;
средняя
квадратичная ошибка средней:

Применение
доверительного интервала для
прогнозирования увеличивает степень
надежности прогноза, но, тем не менее,
прогнозируемый показатель равен среднему
уровню. Чтобы учесть вариацию показателя
вокруг средней в прошлом и будущем, для
прогностической величины вычисляют
доверительный интервал:
(9.1)
так как общая
дисперсия, связанная с колебаемостью
выборочной средней и варьированием
уровней ряда вокруг средней, будет равна

где

Если общая
тенденция развития динамического ряда
является линейной или выполняется
неравенство:
где
— остаточная дисперсия, не объясненная
экстраполяцией по среднему абсолютному
приросту;
—
общий прирост показателя от начального
уровня до конечного, то выполняется
экстраполяция по среднему абсолютному
приросту. Прогнозное значение уровня
определяют по формуле:
где
— уровень ряда динамики, принятый за
базу экстраполяции;
— средний абсолютный прирост;
— период упреждения.
Если развитие
ряда динамики списывается геометрической
прогрессией или показательной кривой,
то экстраполяция выполняется по среднему
темпу роста. Прогнозируемый уровень
ряда определяется по следующей формуле:
где
— средний темп роста;
—
уровень ряда динамики, принятый за базу
экстраполяции.
В качестве
базового уровня для экстраполяции
берется последний уровень ряда
,
так как будущее развитие начинается
именно с этого уровня. В некоторых
случаях в качестве базового уровня
лучше брать расчетный уровень,
соответствующий тренду, описывающему
динамический ряд. Для этого определяют
экспоненциальную кривую и на ее основе
находят базовый уровень. Для выбора
базового уровня можно прибегнуть к
усреднению нескольких последних уровней,
т. e.
вычислить экспоненциальную или
геометрическую среднюю нескольких
последних уровней.
Отметим, что
если уровни ряда динамики непрерывно
возрастают за рассматриваемый период,
то средний темп роста вычисляют по
формуле
где
— число цепных темпов роста;
— произведение уровней динамического
ряда;
— цепной темп роста;
— сумма порядковых номеров уровней
динамического ряда;
— начальный уровень ряда.
Если же уровни
ряда динамики в одни годы растут, а в
другие снижаются, то для вычисления
среднего темпа роста можно воспользоваться
следующей формулой:
Доверительный
интервал прогноза по среднему темпу
роста может быть построен в случае,
когда средний темп роста определяется
по экспоненциальной функции.
Указанные
способы экстраполяции тренда динамического
ряда являются весьма приближенными.
Пример 9.1.
Выпуск цемента за период с 1975 по 1990 г.
характеризуется динамическим рядом,
представленным в табл. 9.1.
Проиллюстрируем
построение прогнозов с использованием
средних характеристик данного ряда
динамики: среднего уровня, среднего
абсолютного прироста и среднего темпа
роста.
При экстраполяции
на основе среднего уровня ряда используется
принцип, при котором прогнозируемый
уровень принимается равным среднему
значению уровней в прошлом:
Таблица 9.1
-
Год, t
Производство цемента, млн.т..
Год, t
Производство цемента, млн.т
1975
122
1983
128
1976
124
1984
130
1977
127
1985
131
1978
127
1986
145
1979
123
1987
137
1980
125
1988
139
1981
127
1989
140
1982
124
1990
142
Доверительный
интервал прогноза для средней вычислим
по формуле (9.1):

Табличное
значение t-статистики
Стьюдента
с
= n
— 1 = 15 степенями свободы при уровне
доверия
= 0,05 равно
=
2,13. Среднее квадратичное отклонение,
связанное с выборочной средней и
варьированием уровней ряда вокруг
средней, равно:
Подставив
найденные значения в формулу (9.1), полущим
доверительный интервал (116,1639; 143,9561),
который с доверительной вероятностью
0,95 включает прогнозируемое значение
производства цемента равно:
млн.т.
Считая,
что общая тенденция производства цемента
является линейной, прогноз производства
цемента на 1991г. вычислим по среднему
абсолютному приросту:
За базу экстраполяции примем среднее
арифметическое трех последних уровней
исходного динамического ряда:
Средний
абсолютный прирост
Тогда прогнозное
значение уровня на 1991г.
(млн.т.)
Экстраполяция по
среднему темпу роста осуществляется
по формуле
где
За базу экстраполяции
примем среднее арифметическое трех
последних уровней, т. e.
140,3.
В этом случае прогнозируемый уровень
ряда равен:
(млн.т.)
Доверительные
интервалы прогноза по среднему абсолютному
приросту и среднему темпу роста могут
быть получены в том случае, когда общая
тенденция развития является линейной
или когда средний темп роста определяется
с помощью статистического оценивания
параметров экспоненциальной кривой.
9.2. Прогнозирование
динамики социально-экономических
явлений по трендовым моделям.
Прогнозирование с помощью трендов —
также один из простейших и распространенных
методов статистического прогнозирования.
Суть этого метода заключается во
временной экстраполяции. При этом
предполагается, что:
— период, для
которого построен тренд, достаточен
для выявления тенденции;
— анализируемый
процесс устойчив и обладает инерционностью;
— не ожидается
сильных внешних воздействий на изучаемый
процесс, которые могут серьезно повлиять
на тенденцию развития.
При соблюдении
этих условий экстраполяция осуществляется
путем подстановки в уравнение тренда
значения независимой переменной
,
соответствующей периоду упреждения
(прогноза). Получается точечная оценка
прогнозируемого показателя (в конкретном
году, квартале, месяце, дне) по уравнению,
описывающему тенденцию. Полученный
прогноз является средней оценкой для
прогнозируемого интервала времени, так
как тренд характеризует некоторый
средний уровень на каждый момент времени.
Отдельные наблюдения, как правило,
отклоняются от него в прошлом. Естественно
ожидать, что подобные отклонения будут
происходить и в будущем. Поэтому
определяется область, в которой с
определенной вероятностью следует
ожидать прогнозируемое значение, т. e.
вычисляется доверительный интервал:
,
(9.2)
где
— точечный прогноз на момент
+
;
— табличное значение
-критерия
Стьюдента с
степенями свободы при уровне доверия
;
— число параметров тренда;
— средняя квадратичная ошибка тренда:

В основу расчета
доверительного интервала прогноза
положен показатель, определяющий
колеблемость ряда заданных значений
признака. Чем выше эта колеблемость тем
менее определено положение тренда и
тем уже должен быть интервал для вариантов
прогноза при одном и том же уровне
доверия. В качестве такого показателя
ряда наблюдаемых значений признака
обычно рассматривается среднее
квадратичное отклонение фактических
наблюдений от расчетных, полученных
при выравнивании динамического ряда,
т. e.
средняя квадратичная ошибка тренда.
Доверительный
интервал (9.1) учитывает неопределенность,
связанную с положением тренда. Но он
должен учитывать также и возможность
отклонения от тренда, т. e.
среднюю квадратичную ошибку прогноза
.
Тогда доверительный интервал прогноза
будет иметь вид
.
(9.3)
Стандартная
ошибка прогноза, когда тренд описывается
прямой
,
вычисляется по формуле:
и доверительный
интервал (9.2) примет вид
(9.4)
где
— среднее квадратичное отклонение
фактических уровней динамического ряда
от расчетных, называемая стандартной
ошибкой тренда; К — величина, зависящая
только от длины динамического ряда и
периода упреждения
;
табличное значение
— критерия Стьюдента с
= n-2
степенями свободы при уровне доверия
.
С увеличением
значения К уменьшаются, а с увеличением
— увеличиваются. Поэтому достаточно
надежный прогноз получается при
относительно большом числе наблюдений
(для линейного тренда n
= 6, для параболического второй степени
n
= 13, для кубического n
= 23), когда период упреждения не очень
большой. При одном и том же
с ростом
доверительный интервал прогноза
увеличивается. Кроме того, доверительный
интервал прогноза при одной и той же
величине средней квадратичной ошибки
будет тем шире, чем выше степень
полинома, характеризующего тренд.
Доверительные
интервалы для линейного тренда,
изображены на рис. 9.1.
Рис.
9.1
Проиллюстрируем
нахождение прогноза по уравнению тренда
и построение доверительного интервала
на примере.
Пример
9.2. Рассмотрим
динамический ряд, характеризующий
производительность труда с февраля
1988г. по апрель 1989г. (см. пример 3.7). Для
данного ряда наилучшей функцией,
характеризующей тренд, была признана
прямая
,
поэтому прогностическая модель имеет
вид:
.
Прогнозирование
с помощью этой модели осуществляется
весьма просто: необходимо вместо
в уравнение подставить нужное значение
и найти прогноз. Так, для прогнозирования
производительности труда в апреле
1989г. нужно подставить
=
15, вследствие чего
Если прогноз
необходимо сделать в году
,
a
период упреждения равен
,
то в прогностическую модель подставляется
значение
,
где n
= 14 соответствует марту 1989г. Доверительные
интервалы найдем, используя выражение
(9.3). Необходимые для этого значения
можно определить из соответствующей
таблицы (см. [19,прил. 7]). Результаты
вычислений сведены в табл. 9.2.
Таблица 9.2
-
Месяц
и год, t
Факти-
ческий
уровень
Выравнен-
ное значе-
ние и про-
гноз
90% доверительный
интервал
нижняя
граница
верхняя
граница
02.1988
20
22,72
2,72
—
—
—
03.1988
24
24,63
0,63
—
—
—
04.1988
28
26,54
1,46
—
—
—
05.1988
30
28,45
1,55
—
—
—
06.1988
31
30,36
0,64
—
—
—
07.1988
33
32,27
0,73
—
—
—
08.1988
34
34,18
0,18
—
—
—
09.1988
37
36,09
0,91
—
—
—
10.1988
38
38,00
0,0
—
—
—
11.1988
40
39,91
0,09
—
—
—
12.1988
41
41,82
0,82
—
—
—
01.1989
43
43,73
0,73
—
—
—
02.1989
45
45,64
0,64
—
—
—
03.1989
48
47,55
0,45
—
—
—
04.1989
—
49,46
1,15
2,0462
47,11
51,81
05.1989
—
51,37
1,15
2,1000
48,95
53,78
06.1989
—
53,28
1,15
2,1590
50,80
55,76
Среднее
квадратичное отклонение равно 1,15. Из
таблицы видим, что доверительные
интервалы оказались достаточно широкими
— свыше 9% прогнозируемого уровня.
Этот пример
показывает, что экстраполяция по тренду
— достаточно грубая операция, основывающаяся
на целом ряде допущений.
9.3.
Построение доверительных интервалов
для полиномиальных трендов.
При построении доверительных интервалов
прогнозов будет предполагать, что ошибки
прогнозов связаны только с ошибками в
оценках параметров прогностических
моделей.
Предположим,
что тренд описывается прямой, квадратичной
и кубической параболами. Для построения
доверительных интервалов прогнозов,
определяемых линейным и параболическим
трендами, определяем стандартные ошибки
прогноза по формулам:
— для линейного
тренда
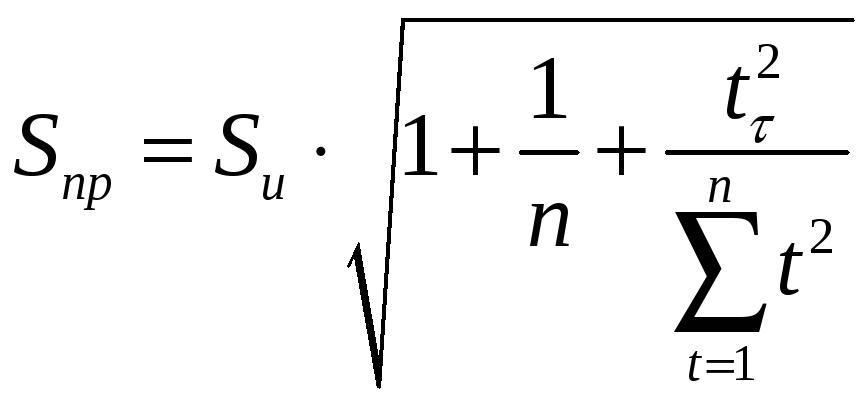
— для тренда,
определяемого параболой второго порядка,

— для тренда,
определяемого параболой третьего
порядка,

Сопоставляя
подкоренные выражения стандартных
ошибок, видим, что при одном и том же
значении
доверительный интервал прогноза тем
шире, чем выше степень полинома,
характеризующего тренд. Это объясняется
тем, что дисперсия уравнения тренда
определяется как взвешенная сумма
дисперсий соответствующих параметров
уравнений. Хотя средняя квадратичная
ошибка тренда является не единственной
характеристикой, определяющей ширину
доверительного интервала, однако она
оказывает преобладающее влияние на эту
величину.
9.4.
Построение доверительных интервалов
для трендов, приводимых к линейному.
Процедура построения доверительных
интервалов полностью переносится и на
случаи, когда уравнение кривой может
быть после некоторых преобразований
сведено к линейному тренду. Оценивание
параметров преобразованных уравнений,
как было указано ранее, осуществляется
методом наименьших квадратов.
В
практике криволинейного выравнивания
широко распространены два вида
преобразований: логарифмирование и
обратное преобразование
.
При этом возможно преобразование как
зависимой переменной
,
так и независимой
или одновременно той и другой.
Рассмотрим
процедуру построения доверительного
интервала прогноза для модифицированной
экспоненты
Прологарифмировав
уравнение, получим линейную функцию от
:
.
Пусть
асимптота
задана, т.е.
,
и не содержит ошибки. Обозначим
.
Тогда доверительный интервал прогноза
для модифицированной экспоненты будет
определяться как доверительный интервал
(9.3) для прямой, т.е.
,
где
среднее квадратичное отклонение от
тренда
.
Зная границы доверительного интервала
для
,
легко определить доверительные границы
прогноза для
:
.
(9.5)
Так
как экспоненциальная кривая
логарифмированием преобразуется к виду
,
то доверительный интервал прогноза
имеет вид
.
(9.6)
В доверительных
интервалах (9.4) и (9.5)

Пример
9.3.
В табл. 9.3 дан динамический ряд,
характеризующий объем продаж.
Таблица
9.3
-
Год
Объем продаж
,
млн.р.Год
Объем продаж
,
млн.р.1971
288
1981
765
1972
308
1982
823
1973
345
1983
877
1974
382
1984
915
1975
436
1985
974
1976
535
1986
1035
1977
562
1987
1128
1978
603
1988
1232
1979
650
1989
1274
1980
681
1990
1318
Для
выбора функции тренда применим метод
характеристик. Построив графики
скользящих средних приростов и их
характеристик, сделаем вывод о том, что
тренд описывается показательной функцией
.
Прологарифмировав уравнение, получим
прямую
,
оценку параметров которой осуществим
методом наименьших квадратов. Итак,
наилучшей функцией, характеризующей
объем продаж, является функция
.
Для
построения доверительного интервала
прогноза вычислим прежде всего среднее
квадратичное отклонение:
.
Используя
формулу (9.5), строим доверительные
интервалы прогноза для периода упреждения:
Значения
коэффициента
будут равны соответственно:

,
Значение
квантиля
,
взятое из таблицы распределения Стьюдента
при заданном уровне значимости
и
степенях свободны, равно
.
Вычислим для
значения
:
Тогда
доверительные интервалы, для
,
будут иметь вид:
Прогноз
для
составит
соответственно:
Вычисленные
значения прогноза принадлежат
соответствующим доверительным интервалам.
Отметим еще раз,
что процедура разработки прогноза с
использованием аналитического
выравнивания тренда состоит из
предварительного выбора одной или
нескольких кривых, которые наилучшим
образом соответствуют характеру
изменения ряда динамики, оценки параметров
выбранных кривых, проверки их адекватности
прогнозируемому процессу, окончательного
выбора кривой роста и вычисления
точечного и интервального прогнозов.
9.5.
Прогнозирование методом экспоненциального
сглаживания.
Вначале введем понятие экспоненциальной
средней.
При вычислении скользящих средних –
простой и взвешенной – всем уровням
динамического ряда присваивались
одинаковые веса. Вес отдельного наблюдения
указывает на часть вклада его значения
в значение средней. В случае простой
скользящей средней эта часть равна
для наблюдений, входящих в среднюю, и
нулю для наблюдений, отсутствующих в
ней. При этом недавние данные имеют тот
же вес, что и данные, относящиеся к
далекому прошлому (старые). Однако
понятно, что недавние данные имеют более
важное значение и должны иметь больший
вес. Поэтому предлагается процедура
усреднения с разными весами. При этом
система весов образует ряд, в котором
веса убывают во времени по экспоненциальному
закону:
,
.
Сумма этого ряда
стремится к единице при неограниченном
увеличении числа слагаемых.
Используя
экспоненциально взвешенные веса,
экспоненциально взвешенную среднюю
первого порядка будем вычислять по
формуле
, (9.7)
которую можно
преобразовать к виду:
(9.8)
На основе этого
уравнения строятся другие модели
экспоненциального сглаживания.
Иногда при
построении моделей прибегают к вычислению
экспоненциально взвешенных средних
более высоких порядков, т.е. средних,
получаемых путем многократного
экспоненциального сглаживания. Такая
средняя вычисляется по формуле:
(9.9)
Из этой формулы
легко получаются выражения:
Экспоненциально
взвешенная средняя имеет ряд преимуществ
перед традиционной скользящей средней.
1.
Для вычисления экспоненциально взвешенной
средней
используется предыдущая экспоненциально
взвешенная средняя
и последнее значение уровня
.
2. Для построения
прогноза по экспоненциально взвешенной
средней необходимо задать начальную
оценку прогноза. При поступлении новых
данных прогнозирование можно продолжать
незамедлительно, т.е. нет необходимости
заново строить процедуру вычисления
прогноза.
3. В экспоненциально
взвешенной средней значения весов
убывают со временем, т.е. нет такой точки,
на которой веса обрываются.
Метод
экспоненциально взвешенной средней
разработан для анализа динамических
рядов, состоящих из большего числа
наблюдений. Поэтому, если динамические
ряды слишком короткие (
уровней) и в случае, когда темпы роста
и прироста велики, метод не “успевает”
отразить все изменения. Метод тем точнее,
чем больше число наблюдений (уровней
динамического ряда).
Рассмотрим
теперь, как применяется метод
экспоненциально взвешенной средней
при прогнозировании экономических
показателей.
Предположим,
что динамический ряд представлен в виде
,
где
— тренд;
— случайная компонента. Если на изучаемом
интервале времени коэффициенты
уравнения, описывающего тренд, остаются
неизменными, то для построения модели
прогноза можно использовать метод
наименьших квадратов. Однако в течение
анализируемого периода коэффициенты
уравнения тренда изменяются во времени.
И так как динамические ряды, характеризующие
экономические процессы, содержат
небольшое число уровней, применение
метода наименьших квадратов для оценки
параметров модели прогноза может
привести к существенным ошибкам. Поэтому
применяется метод
экспоненциально взвешенной средней,
в котором новым данным придаются большие
веса, чем старым.
Пусть
тренд определяется линейной функцией
.
Как показал Р.Г. Браун, оценки коэффициентов
и
выражаются через экспоненциально
взвешенные средние по формулам:
.
Прогноз для
случая, когда тренд характеризуется
линейной функцией, вычисляется по
формуле
.
(9.10)
Чтобы
воспользоваться формулой (9.9) для
прогнозирования, нужно определить
значения параметров
и
,
которые выражаются через экспоненциально
взвешенные средние. А из формул (9.7) и
(9.8) следует, что для вычисления
и
необходимо задать начальные значения
и
или в общем случае
,
которые будем называть в дальнейшем
начальными условиями.
Начальные
условия либо задают исходя из экономических
соображений (например, из величины
лага), либо вычисляют по формулам:
В
качестве значений коэффициентов
и
нужно брать коэффициенты уравнения
тренда, полученные методом наименьших
квадратов, т.е. найденные при решении
системы
Затем вычисляются
экспоненциально взвешенные средние
первого и второго порядков:
,
,
…
,
,
…
Ошибка прогноза
при использовании доверительного
интервала (9.3) определяется по формуле

где
– средняя квадратичная ошибка,
характеризующая отклонения от линейного
тренда:

При
использовании прогностической модели
(9.10) одной из основных проблем является
выбор оптимального значения параметра
сглаживания
,
где
.
От численного значения
зависит, насколько быстро будет
уменьшаться вес предшествующих
наблюдений, т.е. насколько быстро будет
уменьшаться степень их влияния на
сглаженный уровень. Это значит, что
чувствительность экспоненциально
взвешенной средней в целях повышения
адекватности прогностической модели
может быть в любой момент изменена путем
изменения значений
.
Чем больше
,
тем выше чувствительность средней. Чем
меньше значение
,
тем устойчивее становится экспоненциально
взвешенная средняя. Если подходящими
оказываются более высокие значения
,
это указывает на нарушение условий
стационарности и означает, что
экспоненциально взвешенная средняя
становится неприемлемой для прогнозирования.
Значения
при условии равенства среднего значения
степени старения данных можно выбирать,
используя формулу
или
.
Значения
,
используемые в области экономического
прогнозирования, находятся в пределах
от 0,05 до 0,3. Длина усреднения в скользящем
среднем с точки зрения чувствительности
прогноза может быть найдена в соответствии
с
из таблицы
-
0,05
0,1
0,2
0,3
39
19
9
6
Достоинство
метода экспоненциально взвешенной
средней по сравнению с другими методами
состоит в его точности, которая
увеличивается с увеличением числа
уровней динамического ряда. Но остается
нерешенной проблема выбора оптимального
значения параметра сглаживания
и начальных условий. Точность прогноза
по этому методу падает с увеличением
горизонта прогнозирования.
Пример
9.4.
Рассмотрим динамический ряд, характеризующий
производство цемента (таблица 9.4).
.
Таблица
9.4
-
Год
Производство цемента
,
млн. т.
Год
Производство
цемента
,
млн. т.
Год
Производство цемента
,
млн. т
1975
122
1981
127
1987
137
1976
124
1982
124
1988
139
1977
127
1983
128
1989
140
1978
127
1984
130
1990
142
1979
123
1985
131
20811980
125
1986
135
Для
построения тренда
описывающего динамический ряд, начало
координат было перенесено в середину
ряда. Тогда система нормальных уравнений
для оценки параметров тренда упрощается:
Решая
ее, находим:
.
Уравнение тренда имеет вид:
.
Для
прогноза выпуска цемента на 1991 г.
воспользуемся формулой (9.10). Оценки
коэффициентов
и
найдем из выражений:
которые
содержат экспоненциально взвешенные
средние
и
и
параметр
. Параметр сглаживания
положим равным 0,15, так как для
рекомендуется брать
в нашем примере
.
Вычисление
и
осуществим по рекуррентной формуле
(9.9), предварительно определив начальные
условия
и
,
,
где,
и
— коэффициенты уравнения тренда. Тогда:
,
Затем
вычисляем
и
,
и
осуществляем прогноз на 1976 г. Далее по
рекуррентной формуле (9.9) вычисляем
новые
и
:
,
,
и по
ним находим
и
которые используем для прогноза
производства цемента на 1977 г., и т.д. В
таблице 9.5 приведены:
— экспоненциально
взвешенные средние, вычисленные по
формуле (9.9);
-соответствующие
коэффициенты
и
;
— результаты
прогноза и отклонения фактических
уровней от прогнозируемых в случае
ретроспективного прогноза;
— указан прогноз
производства цемента на 1991 г.
Таблица
9.5
|
Год |
Производст-во цемента, млн. т |
|
|
|
|
Прогноз |
Отклонение
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1976 |
124 |
125,82 |
123,36 |
128,28 |
0,43 |
128,71 |
-4,71 |
|
1977 |
127 |
125,60 |
123,70 |
127,50 |
0,34 |
127,84 |
-0,84 |
|
1978 |
127 |
125,81 |
124,02 |
127,60 |
0,32 |
127,95 |
-0,92 |
|
1979 |
123 |
125,39 |
124,23 |
126,55 |
0,20 |
126,75 |
-3,75 |
|
1980 |
125 |
125,33 |
124,39 |
126,27 |
0,17 |
126,44 |
-1,44 |
|
1981 |
127 |
125,58 |
124,57 |
126,59 |
0,18 |
126,77 |
0,23 |
|
1982 |
124 |
125,39 |
124,69 |
125,99 |
0,11 |
126,10 |
-2,10 |
|
1983 |
128 |
125,74 |
124,85 |
126,63 |
0,16 |
126,69 |
1,31 |
|
1984 |
130 |
126,38 |
125,08 |
127,68 |
0,23 |
127,91 |
2,09 |
|
1985 |
131 |
127,07 |
125,38 |
128,76 |
0,30 |
129,06 |
1,94 |
|
1986 |
135 |
128,26 |
125,81 |
130,71 |
0,43 |
131,14 |
3,86 |
|
1987 |
137 |
129,57 |
126,37 |
132,77 |
0,56 |
133,33 |
3,67 |
|
1988 |
139 |
130,98 |
127,06 |
134,90 |
0,69 |
135,59 |
3,41 |
|
1989 |
140 |
132,33 |
127,85 |
136,81 |
0,79 |
137,60 |
2,40 |
|
1990 |
142 |
133,78 |
128,74 |
138,82 |
0,89 |
139,71 |
2,99 |
|
1991 |
— |
135,01 |
129,68 |
140,34 |
0,94 |
141,28 |
— |
Для
прогноза производства цемента на 1991 г.
использовались следующие значения
экспоненциально взвешенных средних:
,
и оценки коэффициентов модели
,
.
Ошибку прогноза вычислим по формуле
где
средняя квадратичная ошибка
Тогда
доверительный интервал прогноза
определяется в виде (9.3), где
— квантиль распределения Стьюдента при
уровне доверия
и числе степеней свободы
,
равный
.
Подставив значения
и
,
получим доверительный интервал прогноза
.
9.6.
Прогнозирование методом гармонических
весов.
Автор метода
гармонических весов
польский статистик З. Хевиг предложил
проводить экстраполяцию по скользящему
тренду. При этом отдельные точки ломаной
линии взвешиваются с помощью гармонических
весов, что позволяет более поздним
уровням динамического ряда придавать
больший вес.
Рассмотрим
временной ряд
,
математическая модель которого имеет
вид
,
где
—
неслучайная функция времени (тренд);
— стационарная случайная компонента.
Если
нет достаточно достоверной априорной
информации о закономерностях изменения
изучаемого экономического явления, то
простая экстраполяция по тренду может
привести к существенным ошибкам. Поэтому
условно можно предположить, что некоторым
приближением фактического тренда
— является ломаная линия, каждое звено
которой сглаживает заданное число
уровней динамического ряда
.
Таким образом, ломаную линию можно
представить как скользящий тренд.
Проводя экстраполяцию по скользящему
тренду и взвешивая при этом отдельные
точки ломаной линии, с тем чтобы более
поздним наблюдениям придать больший
вес, получаем прогноз. Доверительный
интервал для прогнозируемых показателей
строится с использованием неравенства
Чебышева.
Для
применения метода гармонических весов
ряд динамики разбивается на интервалы,
каждый из которых содержит 3 – 5 уровней.
Число интервалов
меньше
.
Для каждого интервала определяется
линейный тренд
Причем
для
для
для
.
Оценивание
параметров скользящего тренда
осуществляется методом наименьших
квадратов. Вычислив оценки параметров
и
,
получим
уравнение.
Вычислим далее значение
в
точках
,
где
.
Для каждого уравнения
получим число значений функции
,
равное числу уровней, содержащихся в
интервале скольжения. Образуем множества
,
значений функции —
,
для которых
.
Эти функции обозначим
,
а число таких функций —
.
Вычислим средние функций, содержащихся
в построенных множествах:
(9.11)
Соединив
точки
отрезками прямой, получим тренд
исследуемого динамического ряда в виде
ломаной линии.
Затем
проверим гипотезу о том, что отклонения
от скользящего тренда имеют случайный
характер. Для проверки гипотезы
,
состоящий в том, что отклонения от
скользящего тренда образуют стационарный
процесс, строится автокорреляционная
функция, которая представляет собой
множество коэффициентов корреляции
между динамическим рядом, состоящим из
отклонений
,
и этим же рядом, сдвинутым относительно
первоначального положения на
моментов
времени. Нормированная автокорреляционная
функция отклонений вычисляется по
формуле
(9.12)
где
Величину
называют сдвигом.
Сдвиг, которому соответствует наибольший
коэффициент автокорреляции, называют
временным
лагом.
График нормированной автокорреляционной
функции называют коррелограммой.
Для
построения коррелограммы на оси абсцисс
откладывают значения
,
а на оси ординат — значения коэффициентов
автокорреляции
.
Затем точки с координатами
соединяют
отрезками прямой. В результате получают
ломаную линию, которая и называется
коррелограммой.
При
вычислении коэффициентов автокорреляции
с ростом
число коррелируемых пар уменьшается,
а известно, что при небольшом числе
наблюдений существенными оказываются
лишь большие коэффициенты. Поэтому
наибольшее значение
должно быть таким, чтобы число пар
наблюдений оказалось достаточным для
вычисления коэффициентов автокорреляции
.
На практике ориентируются на правило,
из которого следует, что
.
Значения
автокорреляционной функции образуют
ряд
,
,
…,
(верхний индекс означает число наблюдений,
для которого вычисляется автокорреляционная
функция). Затем исключают из динамического
ряда первый или последний уровень и
вычисляют значения автокорреляционной
функции
,
,
…,
.
Продолжая указанный процесс, исключают
уровней динамического ряда и вычисляют
значения
автокорреляционных
функций. Таким образом, получают
групп
коэффициентов автокорреляции, в каждой
из которых будет
коэффициентов. Отклонения от скользящего
тренда образуют стационарный в широком
смысле процесс, если коэффициенты
автокорреляции, входящие в одну и ту же
группу, однородны.
Проверка
на однородность коэффициентов
автокорреляции
производится следующим образом. Для
каждого
,
входящего в
– ю группу, вычисляют
критерий:
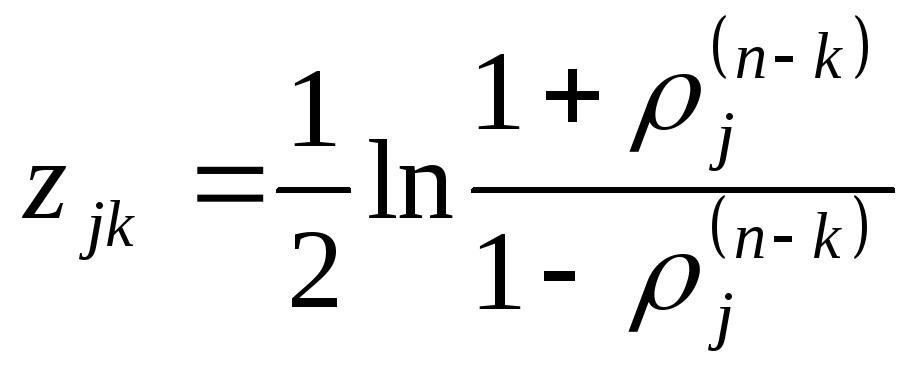
.
Затем
для этой группы находят среднюю
и вычисляют величину
,
(9.13)
которая
распределена по закону
—
квадрат с
степенями свободы. Тогда, сравнивая
вычисленное значение величины (9.13) с
табличным, при
с вероятностью
принимаем гипотезу об однородности
рассматриваемой группы коэффициентов
автокорреляции. Аналогичную проверку
однородности проводим для всех групп
коэффициентов автокорреляции. Если
гипотеза об однородности принимается
для всех групп, то делаем вывод о том,
что отклонения от скользящего тренда
образуют стационарный в широком смысле
случайный процесс. Кроме того, если
значения автокорреляционной функции,
вычисленные для ряда отклонений от
скользящего тренда, уменьшаются, это
значит, что более поздняя информация
сильнее отражается на прогнозируемой
величине, чем более ранняя.
Установив, что
отклонения образуют стационарный
процесс, вычисляем приросты, равные
разностям средних значений скользящих
трендов:
.
Средняя приростов
вычисляется по формуле
,
где
гармонические коэффициенты, удовлетворяющие
следующим условиям:
,
.
(9.14)
Гармонические
коэффициенты
определяем так, чтобы более поздним
наблюдениям придавались большие веса.
Для этого полагаем
,
где
,
т.е.
.
Следовательно,
и гармонические коэффициенты
удовлетворяют условиям (9.14).
Предположим,
что приросты
являются значениями случайной величины
с математическим ожиданием
и дисперсией
.
Тогда
их оценками будут средняя приростов
и статистическая дисперсия

Применив неравенство Чебышева, можно
записать:
,
где
заданное положительное число;
. Так как значения
коррелированны между собой, то
в неравенстве Чебышева является величиной
переменной, вычисляемой по формуле
.
Прогнозирование
методом гармонических весов производится
путем прибавления к последнему значению
ряда динамики
среднего прироста
,
т.е.
.
Доверительный интервал прогноза имеет
вид:
.
Пример
9.5.
Рассмотрим динамический ряд, характеризующий
производство цемента (см. таблицу 9.5).
Этот динамический ряд не имеет
скачкообразных изменений и достаточно
хорошо описывается линейным трендом.
Поэтому для дисконтирования уровней
ряда динамики с целью определения
прогноза производства цемента в 1991 г.
применим метод гармонических весов.
Построим вначале скользящий тренд. Для
этого разобьем исходный ряд динамики
на интервалы, каждый из которых содержит
5 уровней. Для каждого интервала скольжения
строим методом наименьших квадратов
линейный тренд
.
Так, первый интервал скольжения состоит
из уровней 122, 124, 127, 127, 123, то система
нормальных уравнений для оценки
параметров, имеет вид
откуда
находим
,
.
Следовательно, линейный тренд для
первого интервала скольжения выражается
уравнением
Аналогично
определяем параметры уравнений для
всех
интервалов скольжения:
С
помощью построенных уравнений определим
значения
скользящего тренда по формуле (9.11).
При
имеем
При
имеем
два значения функций, для которых:
,
,
откуда
Аналогично
находим все остальные значения
:
Проверим
теперь гипотезу о том, что отклонения
от скользящего тренда имеют случайный
характер. Для этого вычислим нормированную
автокорреляционную функцию (9.12) для
…
Значения автокорреляционной функции
для
равны:
Значения
автокорреляционной функции для
после исключения первого отклонения
будут равны:
Пусть
,
тогда:
Отметим,
что для
значения коэффициентов автокорреляции
можно подвергать сомнению. Но для
подтверждения убывания коэффициентов
автокорреляции вычисление проводилось
до значения
.
И тогда, с уверенностью, можно утверждать,
что значения автокорреляционной функции
постоянно затухают. Проверим однородность
коэффициентов автокорреляции. Для этого
вычислим
критерий:
и
по формуле (9.13). Значения
для трех групп коэффициентов автокорреляции
равны:
Вычисленные
значения меньше табличного
следовательно, с вероятностью
можно
утверждать, что отклонения от тренда
образуют стационарный в широком смысле
случайный процесс.
Затем
вычисляем приросты по формуле
:
и
гармонические веса
:
Гармонические
коэффициенты вычисляем по формуле
Все эти коэффициенты
положительны, их сумма равна единице.
Найдем средний
прирост:
Тогда прогноз
производства цемента на 1991 г. равен:
Для
построения доверительного интервала
вычислим среднее квадратичное отклонение:

Найдем
функцию
Так
как
,
то
.
Произведение
.
Пусть
,
тогда вероятность того, что прогноз
производства цемента выйдет за пределы
доверительного интервала, не превосходит
0,04, что следует из неравенства Чебышева
так
как
.
Доверительный интервал имеет вид:
.
Еще раз
подчеркнем, что метод гармонических
весов применяется, когда в ряду динамики
отсутствуют сезонные и циклические
колебания. Следовательно, мы спрогнозировали
только значение детерминированной
компоненты динамического ряда.
9.7.
Особенности прогнозирования сезонных
колебаний.
В прогностической модели сезонность
учитывается, как правило, посредством
декомпозиции прогностических методов.
При этом предполагается, что характеристики
движения ряда могут быть выделены,
изучены и оценены изолированно друг от
друга. Окончательный же прогноз будет
осуществляться сведением прогнозов
различных элементов в один.
При
прогнозировании сезонного ряда
необходимо определить, как изменение
значения переменной в данный момент
(на данный месяц) связано с изменением
значения этой переменной, отстоящей на
сезонный цикл (чаще всего, равный одному
году). А так как каждый момент времени
принадлежит одному циклу, задача
заключается в установлении формы
сезонной зависимости. Для решения
сформулированной задачи период наблюдения
должен быть не менее четырех лет. Сезонные
колебания численно описываются индексами
сезонности. Они, по определению,
представляют собой отношение текущего
значения к среднему значению этого
показателя, соответствующему моментам
времени, лежащим внутри цикла. При
прогнозировании сезонных рядов необходимо
помнить последние L
индексов сезонности (L
= 12 для календарных месяцев, L
= 4 для кварталов). Сумма индексов
сезонности должна быть равна 12 (или 4
для поквартальных данных). В противном
случае их выправляют. Это необходимое
условие (средняя индексов равна единице)
для несмещенности прогнозов. Многие
методы декомпозиции предполагают в
какой-либо форме наличие линейного
тренда, вследствие чего при построении
прогноза учитывают связанный с этим
линейный рост. Сезонный анализ данных
без выделения и оценивания линейного
тренда привел бы к смещению индексов
сезонности, т.е. к заметному отличию
суммы этих индексов за год от 12.
Рассмотрим различные
прогностические модели.
Сезонно-декомпозиционная
прогностическая модель
Холта — Винтера основана на применении
метода экспоненциально взвешенной
средней. Указанная модель предполагает
оценку стационарно-линейного и сезонного
факторов. Оценка стационарного фактора,
т.е. оценка среднемесячного значения
показателя, независимо от времени года
проводится по формуле
,
где
предыдущее значение экспоненциально
взвешенной средней. При этом предполагается,
что динамический ряд фактических данных
очищен от сезонности делением его на
сезонный индекс, соответствующий моменту
времени
,
т.е. сдвинутому на
единиц времени назад.
Оценка линейного
роста вычисляется на основе модели
роста Холта
,
где
прошлый показатель роста. А оценка
сезонной компоненты, т.е. адаптация
индекса сезонности, предполагает
вычисление индекса сезонности (отношение
значения текущего уровня к среднестационарному
значению) и определение экспоненциально
взвешенной средней его текущего значения
.
При
изолированной оценке трех компонент
динамического ряда, определяющих
движение процесса, прогноз на
моментов времени вперед
строится следующим образом. Суммируются
оценки линейного роста
и стационарного фактора
,
и результат с учетом сезонности
домножается на соответствующее значение
индекса сезонности
:
(9.15)
Тамара
установил, что в большинстве практических
ситуаций значения
и
равны соответственно 0,2; 0,2; 0,5. Винтер
также получил близкие значения этих
коэффициентов (0,2; 0,2; 0,6 соответственно),
приводящие к наименьшей стандартной
ошибке прогноза.
Модель
Холта — Винтера в практике прогнозирования
сезонных временных рядов встречается
чаще всего. Ее прогностическая точность
не уступает точности других, более
сложных, моделей поведения сезонно
изменяющихся временных рядов (средняя
абсолютная процентная ошибка по этой
модели в большинстве случаев меньше
%
).
Прогнозирование
сезонных колебаний можно осуществлять
также посредством формулы
где
прогнозируемое значение уровня
динамического ряда;
—
средний индекс сезонности
-го
квартала;
—
уравнение тренда;
— случайная
компонента.
При прогнозировании
сезонных колебаний используются средние
индексы по расположению, которые
вычисляются следующим образом. В
ранжированном ряду показателей
сезонности для каждого квартала
отбрасываются наибольшие и наименьшие
значения. Затем вычисляется средняя
арифметическая из центральных значений
показателей сезонности. Если число
индексов четное, то для вычисления
средней берут 4 или 6 центральных точек,
если же нечетное, — то 3 или 5. Такая средняя
по расположению не подвержена влиянию
крайних значений.
Если динамический
ряд можно представить в виде ряда Фурье
и предположить,
что в будущем периоде сохранится эта
же амплитуда колебаний, то можно
попытаться оценить значение исследуемого
показателя на перспективу. Однако при
вычислении значений функции следует
исходить из значений предполагаемого
тренда, а не от среднего уровня. При
этом трудно оценить погрешность. Поэтому
вычисленную ошибку аппроксимации
переносят в будущем и строят доверительные
интервалы. Среднюю ошибку аппроксимации
вычисляют для фактических данных с
учетом тренда. Прогностическая
модель записывается в виде

где
—
тренд динамического ряда.
Для того чтобы
построенные амплитуды лучше соответствовали
амплитудам будущего периода, нужно
брать небольшой период, предшествующий
предсказываемому.
Пример
9.6.
Рассмотрим данные примера 7.6
и воспользуемся прогностической моделью
для
вычисления прогноза объема ежеквартальной
продажи на 1991 г. Значения индексов
возьмем из табл.
7.6,
будем
рассчитывать по уравнению тренда
.
Случайную компоненту оценим с помощью
доверительного интервала
,
где
— квантиль распределения Стьюдента,
определяемый из таблицы в зависимости
от доверительной вероятности
и числа степеней свободы
— определяется из ретроспективного
прогноза.
Прогностические
модели для расчета объема ежеквартальных
продаж для I
– IV
кварталов имеют соответственно следующий
вид:
(9.16)
Вначале
рассчитаем ретроспективный прогноз и
средние квадратичные отклонения прогноза
от фактических данных, т.е.
:

.
Из
таблицы критических значений
найдем
для числа степеней свободы
и уровня доверия
.
Тогда доверительные оценки значений
объема продаж в I-IV
кварталах равны соответственно:
Осуществим
прогноз объема продаж на 1991 г., используя
прогностические модели (9.16), и укажем
доверительные интервалы (табл. 9.6).
Таблица
9.6
-
Квартал
Прогноз
Доверительный интервал
I
25,13 (
=37)
(24,05; 26,21)
II
26,11 (
=39)
(25,29; 26,93)
III
18,87 (
=41)
(18,28; 19,46)
IV
25,57 (
=42)
(24,53; 26,61)
Как
видим, общая тенденция изменения объема
продаж, установившаяся в изучаемом
периоде, сохранится и на прогнозируемый
период. Заметим, что при ретроспективном
и перспективном прогнозировании мы
использовали такое же изменение времени,
как в примере
7.6.
Рассмотрим
теперь процедуру разработки прогноза
с помощью сезонно-декомпозиционной
прогностической модели Холта-Винтера
(9.15), в которой
— экспоненциально взвешенное среднее
значение поквартального объема продаж:
;
оценка линейного роста:
;
предыдущий показатель роста, вычисляемый
как средний абсолютный прирост
экспоненциально взвешенная средняя
текущего значения коэффициента сезонности
.
Формулу (9.15)
применим для каждого квартала. Сначала
определим прогноз объема продаж на
первый квартал. Рассчитаем начальные
условия:
где
,
взяты из уравнения тренда
а
.
Вычисление
и
осуществим по рекуррентной формуле
(9.9).
Результаты промежуточных расчетов
приведены в табл. 9.7.
Таким
образом, в табл. 9.7 мы определим
,
и оно равно 22,8. Значение
— это предыдущий показатель линейного
роста, а
находим
из табл. 7.6.
Таблица
9.7
|
Год |
Объем продаж в I |
|
|
|
|
|
|
|
|
1983 |
18,6 |
19,792 |
19,991 |
19,593 |
-0,050 |
19,5 |
-0,9 |
0,81 |
|
1984 |
21,8 |
19,554 |
19,904 |
19,204 |
-0,087 |
19,8 |
2,0 |
4,00 |
|
1985 |
23,4 |
20,332 |
19,990 |
20,674 |
0,085 |
20,8 |
2,6 |
6,76 |
|
1986 |
22,6 |
20,786 |
20,149 |
21,423 |
0,159 |
21,6 |
1,0 |
1,00 |
|
1987 |
21,9 |
21,009 |
20,121 |
21,897 |
0,222 |
22,1 |
0,8 |
0,64 |
|
1988 |
21,8 |
21,167 |
20,330 |
22,004 |
0,209 |
22,2 |
-0,4 |
0,16 |
|
1989 |
23,1 |
21,554 |
20,575 |
22,533 |
0,245 |
22,8 |
0,3 |
0,09 |
|
1990 |
24,6 |
22,163 |
20,893 |
23,433 |
0,317 |
23,8 |
0,8 |
0,64 |
Тогда:
,
,
.
Применив
формулу (9.15), получим прогноз объема
продаж на первый квартал 1991 г.:
.
Так как
сезонно-декомпозиционная модель Холта
— Винтера основана на применении метода
экспоненциально взвешенной средней,
ошибку прогноза можно вычислить по
формуле
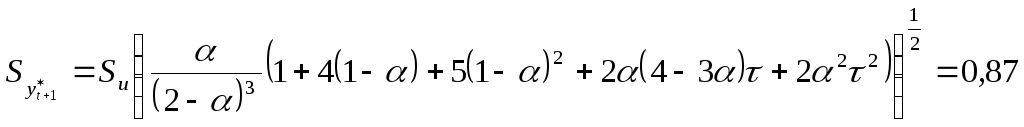
где

Тогда доверительный интервал прогноза
будет иметь вид
Аналогично
проводится процедура вычисления прогноза
объема продаж на второй квартал 1991 г.
Так как уравнение тренда для всех
кварталов одно и то же, начальные условия
также будут одни и те же, т.е.
Используя
результаты промежуточных вычислений,
находим:
,
Тогда прогноз
объема продаж на второй квартал 1991 г.
.
Доверительный
интервал прогноза имеет вид
Для вычисления
прогноза объема продаж на третий квартал
1991 г. найдем:
,
Прогноз объема
продаж
,
a
его доверительный интервал имеет вид
Вычислим прогноз
объема продаж на четвертый квартал 1991
г. Так как
,
то
.
Доверительный
интервал прогноза имеет вид
Значения
прогноза объема продаж, полученные
методом Холта — Винтера, выше, чем
значения, полученные по формуле
но общая тенденция изменения объема
продаж сохраняется и на прогнозируемый
период.
Пример
9.7.
Используя данные о надое молока по
совхозу “Старо Борисов” Борисовского
района Минской области (табл. 9.8), построим
прогноз валового надоя по кварталам на
1991 г.
Таблица
9.8
-
Год
Квартал
Валовой надои молока
,
ц1988
I
1
419,2
II
2
533,6
III
3
511,1
IV
4
398,8
1989
I
5
454,1
II
6
555,9
III
7
612,2
IV
8
459,3
1990
I
9
518,2
II
10
598,7
III
11
624,2
IV
12
554,0
Так
как очевидно, что исследуемый динамический
ряд имеет сезонную компоненту, которая
по определению имеет точную периодичность,
ее (сезонную компоненту) можно представить
суммой гармоник с регулярными частотами
и длинами волн в 12; 6; 4; 3; 2, 4 и 2 месяца.
Поэтому для построения модели сезонной
волны можно применять гармонический
анализ. Наиболее удобным для гармонического
анализа является период с двенадцатью
наблюдениями, так как гармонический
анализ основывается на исследовании
колебаний вокруг среднего уровня.
Наибольшее количество гармоник, которое
можно рассчитать для этого ряда, равно
6. Найдем коэффициенты
,
ряда Фурье
по формулам:
где
. Получим модель сезонной волны в виде
(9.17)
Части общей
дисперсии, учитываемые гармониками,
составляют:
— первая — 27,7 %;
-вторая — 5,9; -третья — 55,3; -четвертая — 2,5;
-пятая — 8,3; —шестая — 0,3 %. Таким образом,
шестью гармониками учитывается 100 %
общей дисперсии. В табл. 9.9 приводятся
расчетные значения по модели (9.17) и их
отклонения от фактических.
Таблица 9.9
-
Год
Квартал
t
Фактические значения
Расчетные значения для шести гармоник
для шести гармоник
Отклонения фактических данных от
расчетных для шести гармоник1988
I
1
419,2
448,5
0,07
-29,3
II
2
533,6
543,7
0,019
-10,1
III
3
511,1
471,34
0,078
39,8
IV
4
398,6
372,1
0,067
26,5
1989
I
5
454,1
473,7
0,043
-19,6
II
6
555,9
496,8
0,116
59,1
III
7
612,2
604,4
0,013
7,8
IV
8
459,3
458,0
0,003
1,3
1990
I
9
518,2
495,2
0,044
23,0
II
10
598,7
595,8
0,005
2,9
III
11
624,2
530,1
0,151
94,5
IV
12
554,0
537,4
0,03
16,6
0,639
Средняя ошибка
аппроксимации
или
5,3%.
Если
предположить, что в будущем сохранится
эта же амплитуда колебаний, можно
попытаться оценить значение исследуемого
показателя на перспективу. При этом
следует исходить не из среднего уровня,
а из значений тренда. Следовательно,
для прогнозирования валового надоя
молока построим тренд исследуемого
динамического ряда. В качестве тренда
возьмем функцию
.
Параметры
и
оценим, решив систему
откуда
=
438,532 и
= 12,522. Таким образом, уравнение тренда
имеет вид
Тогда прогностическая модель запишется
так:
Прогноз ожидаемого
валового надоя молока в совхозе будет
следующим:
— первый квартал
-529,959 ц; — второй — 650,450; — третий — 607,437;
-четвертый — 475 281 ц.
При таком
прогнозе трудно оценить погрешность.
Можно перенести рассчитанную ошибку
аппроксимации в перспективный анализ
и тем самым оценить погрешность прогноза.
Основной задачей при управлении запасами является определение объема пополнения, то есть, сколько необходимо заказать поставщику. При расчете этого объема используется несколько параметров — сколько будет продано в будущем, за какое время происходит пополнение, какие остатки у нас на складе и какое количество уже заказано у поставщика. То, насколько правильно мы определим эти параметры, будет влиять на то, будет ли достаточно товара на складе или его будет слишком много. Но наибольшее влияние на эффективность управления запасами влияет то, насколько точен будет прогноз. Многие считают, что это вообще основной вопрос в управлении запасами. Действительно, точность прогнозирования очень важный параметр. Поэтому важно понимать, как его оценивать. Это важно и для выявления причин дефицитов или неликвидов, и при выборе программных продуктов для прогнозирования продаж и управления запасами.
В данной статье я представила несколько формул для расчета точности прогноза и ошибки прогнозирования. Кроме этого, вы сможете скачать файлы с примерами расчетов этого показателя.
Статистические методы
Для оценки прогноза продаж используются статистические оценки Оценка ошибки прогнозирования временного ряда. Самый простой показатель – отклонение факта от прогноза в количественном выражении.
В практике рассчитывают ошибку прогнозирования по каждой отдельной позиции, а также рассчитывают среднюю ошибку прогнозирования. Следующие распространенные показатели ошибки относятся именно к показателям средних ошибок прогнозирования.
К ним относятся:
MAPE – средняя абсолютная ошибка в процентах
где Z(t) – фактическое значение временного ряда, а 
Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.
Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.
MAE – средняя абсолютная ошибка

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.
После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.
Кроме указанных методов иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.
ME – средняя ошибка
Встречается еще другое название этого показателя — Bias (англ. – смещение) демонстрирует величину отклонения, а также — в какую сторону прогноз продаж отклоняется от фактической потребности. Этот индикатор показывает, был ли прогноз оптимистичным или пессимистичным. То есть, отрицательное значение Bias говорит о том, что прогноз был завышен (реальная потребность оказалась ниже), и, наоборот, положительное значение о том, что прогноз был занижен. Цифровое значение показателя определяет величину отклонения (смещения).
MSE – среднеквадратичная ошибка

RMSE – квадратный корень из среднеквадратичной ошибки

.
SD – стандартное отклонение
где ME – есть средняя ошибка, определенная по формуле выше.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме ниже. Скачать пример расчета в Excel >>>
Связь точности и ошибки прогнозирования
В начале этого обсуждения разберемся с определениями.
Ошибка прогноза — апостериорная величина отклонения прогноза от действительного состояния объекта. Если говорить о прогнозе продаж, то это показатель отклонения фактических продаж от прогноза.
Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.
Точность прогноза в % = 100% – MAPE, встречается еще название этого показателя Forecast Accuracy. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности. Показатель точности прогноза выражается в процентах:
- Если точность прогноза равна 100%, то выбранная модель описывает фактические значения на 100%, т.е. очень точно. Нужно сразу оговориться, что такого показателя никогда не будет, основное свойство прогноза в том, что он всегда ошибочен.
- Если 0% или отрицательное число, то совсем не описывает, и данной модели доверять не стоит.
Выбрать подходящую модель прогноза можно с помощью расчета показателя точность прогноза. Модель прогноза, у которой показатель точность прогноза будет ближе к 100%, с большей вероятностью сделает более точный прогноз. Такую модель можно назвать оптимальной для выбранного временного ряда. Говоря о высокой точности, мы говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Не имеет значения, что именно вы будете отслеживать, но важно, чтобы вы сравнивали модели прогнозирования или целевые показатели по одному показателю – ошибка прогноза или точность прогнозирования.
Ранее я использовала оценку MAPE, до тех пор пока не встретила формулу, которую рекомендует Валерий Разгуляев.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>
Оценка ошибки прогноза – формула Валерия Разгуляева (сайт http://upravlenie-zapasami.ru/)
Одной из самых используемых формул оценки ошибки прогнозирования является следующая формула:
где: P – это прогноз, а S – факт за тот же месяц. Однако у этой формулы есть серьезное ограничение — как оценить ошибку, если факт равен нулю? Возможный ответ, что в таком случае D = 100% – который означает, что мы полностью ошиблись. Однако простой пример показывает, что такой ответ — не верен:
|
вариант |
прогноз |
факт |
ошибка прогноза |
|
№1 |
4 |
0 |
100% |
|
№2 |
4 |
1 |
300% |
|
№3 |
1 |
4 |
75% |
Оказывается, что в варианте развития событий №2, когда мы лучше угадали спрос, чем в варианте №1, ошибка по данной формуле оказалась – больше. То есть ошиблась уже сама формула. Есть и другая проблема, если мы посмотрим на варианты №2 и №3, то увидим, что имеем дело с зеркальной ситуацией в прогнозе и факте, а ошибка при этом отличается – в разы!.. То есть при такой оценке ошибки прогноза нам лучше его заведомо делать менее точным, занижая показатель – тогда ошибка будет меньше!.. Хотя понятно, что чем точнее будет прогноз – тем лучше будет и закупка. Поэтому для расчёта ошибки Валерий Разгуляев рекомендует использовать следующую формулу:
В таком случае для тех же примеров ошибка рассчитается иначе:
|
вариант |
прогноз |
факт |
ошибка прогноза |
|
№1 |
4 |
0 |
100% |
|
№2 |
4 |
1 |
75% |
|
№3 |
1 |
4 |
75% |
Как мы видим, в варианте №1 ошибка становится равной 100%, причём это уже – не наше предположение, а чистый расчёт, который можно доверить машине. Зеркальные же варианты №2 и №3 – имеют и одинаковую ошибку, причём эта ошибка меньше ошибки самого плохого варианта №1. Единственная ситуация, когда данная формула не сможет дать однозначный ответ – это равенство знаменателя нулю. Но максимум из прогноза и факта равен нулю, только когда они оба равны нулю. В таком случае получается, что мы спрогнозировали отсутствие спроса, и его, действительно, не было – то есть ошибка тоже равна нулю – мы сделали совершенно точное предсказание.
Визуальный метод – графический
Визуальный метод состоит в том, что мы на график выводим значение прогнозной модели и факта продаж по тем моделям, которые хотим сравнить. Далее сравниваем визуально, насколько прогнозная модель близка к фактическим продажам. Давайте рассмотрим на примере. В таблице представлены две прогнозные модели, а также фактические продажи по этому товару за тот же период. Для наглядности мы также рассчитали ошибку прогнозирования по обеим моделям.
По графикам очевидно, что модель 2 описывает лучше продажи этого товара. Оценка ошибки прогнозирования тоже это показывает – 65% и 31% ошибка прогнозирования по модели 1 и модели 2 соответственно.


Недостатком данного метода является то, что небольшую разницу между моделями сложно выявить — разницу в несколько процентов сложно оценить по диаграмме. Однако эти несколько процентов могут существенно улучшить качество прогнозирования и планирования пополнения запасов в целом.
Использование формул ошибки прогнозирования на практике
Практический аспект оценки ошибки прогнозирования я вывела отдельным пунктом. Это связано с тем, что все статистические методы расчета показателя ошибки прогнозирования рассчитывают то, насколько мы ошиблись в прогнозе в количественных показателях. Давайте теперь обсудим, насколько такой показатель будет полезен в вопросах управления запасами. Дело в том, что основная цель управления запасами — обеспечить продажи, спрос наших клиентов. И, в конечном счете, максимизировать доход и прибыль компании. А эти показатели оцениваются как раз в стоимостном выражении. Таким образом, нам важно при оценке ошибки прогнозирования понимать какой вклад каждая позиция внесла в объем продаж в стоимостном выражении. Когда мы оцениваем ошибку прогнозирования в количественном выражении мы предполагаем, что каждый товар имеет одинаковый вес в общем объеме продаж, но на самом деле это не так – есть очень дорогие товары, есть товары, которые продаются в большом количестве, наша группа А, а есть не очень дорогие товары, есть товары которые вносят небольшой вклад в объем продаж. Другими словами большая ошибка прогнозирования по товарам группы А будет нам «стоить» дороже, чем низкая ошибка прогнозирования по товарам группы С, например. Для того, чтобы наша оценка ошибки прогнозирования была корректной, релевантной целям управления запасами, нам необходимо оценивать ошибку прогнозирования по всем товарам или по отдельной группе не по средними показателями, а средневзвешенными с учетом прогноза и факта в стоимостном выражении.
Пример расчета такой оценки Вы сможете увидеть в файле Excel.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>
При этом нужно помнить, что для оценки ошибки прогнозирования по отдельным позициям мы рассчитываем по количеству, но вот если нам важно понять в целом ошибку прогнозирования по компании, например, для оценки модели, которую используем, то нам нужно рассчитывать не среднюю оценку по всем товарам, а средневзвешенную с учетом стоимостной оценки. Оценку можно брать по ценам себестоимости или ценам продажи, это не играет большой роли, главное, эти же цены (тип цен) использовать при всех расчетах.
Для чего используется ошибка прогнозирования
В первую очередь, оценка ошибки прогнозирования нам необходима для оценки того, насколько мы ошибаемся при планировании продаж, а значит при планировании поставок товаров. Если мы все время прогнозируем продажи значительно больше, чем потом фактически продаем, то вероятнее всего у нас будет излишки товаров, и это невыгодно компании. В случае, когда мы ошибаемся в обратную сторону – прогнозируем продажи меньше чем фактические продажи, с большой вероятностью у нас будут дефициты и компания не дополучит прибыль. В этом случае ошибка прогнозирования служит индикатором качества планирования и качества управления запасами.
Индикатором того, что повышение эффективности возможно за счет улучшения качества прогнозирования. За счет чего можно улучшить качество прогнозирования мы не будем здесь рассматривать, но одним из вариантов является поиск другой модели прогнозирования, изменения параметров расчета, но вот насколько новая модель будет лучше, как раз поможет показатель ошибки прогнозирования или точности прогноза. Сравнение этих показателей по нескольким моделям поможет определить ту модель, которая дает лучше результат.
В идеальном случае, мы можем так подбирать модель для каждой отдельной позиции. В этом случае мы будем рассчитывать прогноз по разным товарам по разным моделям, по тем, которые дают наилучший вариант именно для конкретного товара.
Также этот показатель можно использовать при выборе автоматизированного инструмента для прогнозирования спроса и управления запасами. Вы можете сделать тестовые расчеты прогноза в предлагаемой программе и сравнить ошибку прогнозирования полученного прогноза с той, которая есть у вашей существующей модели. Если у предлагаемого инструмента ошибка прогнозирования меньше. Значит, этот инструмент можно рассматривать для применения в компании. Кроме этого, показатель точности прогноза или ошибки прогнозирования можно использовать как KPI сотрудников, которые отвечают за подготовку прогноза продаж или менеджеров по закупкам, в том случае, если они рассчитывают прогноз будущих продаж при расчете заказа.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>
Если вы хотите повысить эффективность управления запасами и увеличить оборачиваемость товарных запасов, предлагаю изучить мастер-класс «Как увеличить оборачиваемость товарных запасов».
Источник: сайт http://uppravuk.net/
Время на прочтение
4 мин
Количество просмотров 1K
Вашу компанию легко ввести в заблуждение, если вы думаете, что увеличение прибыли — это всегда повышенные показатели точности прогноза. В российской практике оценка точности прогноза — один из ключевых показателей, на который ориентируются компании. Однако по нашему опыту он переоценен и часто вводит компании в заблуждение относительно его влияния на конечную прибыль. В статье последовательно рассмотрим 5 основных проблем, с которыми сопряжено использование данного показателя. Также предложим варианты их решения.
Прежде всего разберемся, зачем вообще считать точность прогнозирования. Ответов может быть несколько:
-
Выбрать оптимальную модель прогнозирования.
-
Рассчитать страховой запас.
-
Выделить SKU, которые требуют повышенного внимания.
-
Сравнить разные программные продукты.
Оценка точности прогноза определяется через ошибку прогнозирования. Ошибка в данном случае — это разница между фактическим значением спроса и его прогнозным значением. Т.е, чем больше будет ошибка прогнозирования, тем менее точен прогноз. Например, при ошибке прогнозирования 5%, точность прогноза будет составлять 95%. Но самый большой подвох, как увидим дальше, кроется в большом количестве методов расчета ошибки прогнозирования.
В большинстве случаев точность прогнозирования выглядит так:
98.1%
Что может скрываться за этими цифрами? Бесконечное количество метрик, которые считаются совершенно по‑разному, например, таких:
И результаты в каждом случае могут сильно отличаться. Сформулируем первую проблему использования точности прогноза как главного критерия оценки эффективности управления запасами.
Проблема 1. Ошибки прогнозирования могут считаться по разным метрикам, которые дают очень разные результаты и несравнимы между собой.
Чтобы лучше проиллюстрировать эту проблему приведем пример:
На рисунке график продаж булочек за последние 12 дней, а ниже ошибка прогнозирования, рассчитанная по различным методикам.
Как можно увидеть, точность прогноза сильно различается. И этой статистикой можно манипулировать так, как будет удобно. Взяв за основу нужную метрику, некоторые сотрудники могут предоставлять руководству те результаты, которые ожидаются. Или, например, они могу закрывать проект такими цифрами, которые выставят его в выгодном свете. А в некоторых случаях компании могут даже заниматься самообманом, не подозревая об этом и веря, что все идет хорошо.
Решение 1. Фиксировать конкретную метрику оценки точности прогнозирования и методику расчета на уровне компании.
Проблема 2. Как оценить точность прогнозирования для группы товаров и в целом для компании.
Теперь эту метрику нужно как-то агрегировать на всю компания. Допустим, у нас есть 100 000 SKU, продажи которых могут кардинально различаться. Нельзя их просто усреднить. Например, у нас есть два вида товаров — виски и колбаса, которые имеют такие показатели:
Если мы сложим прогнозные и фактические продажи по этим товарам, то они друг друга уравняют. Точность прогнозирования будет 100 %. Но, если смотреть этот показатель отдельно по товарам, все уже не так хорошо.
К тому же, самые внимательные могут заметить, что величина отклонения факта от прогноза у этих товаров одинаковая, но величина ошибки прогнозирования MAPE в одном случае — 50%, а в другом — 100%. Как легко догадаться, это происходит из-за того, что фактические продажи отклоняются в разные стороны. Это еще одна проблема такого подхода. Они ней мы поговорим чуть ниже.
Для решения этой проблемы можно пойти по пути взвешивания этих ошибок в соответствии с их вкладом в важные для компании критерии. Это может быть прибыль или объем продаж.
Например, мы взвешиваем виски и спички по среднему спросу. И в этом случае ошибка сдвигается к тому товару, который больше продается. В итоге мы получаем более-менее верную оценку точности прогнозирования.
Решение 2. Использовать взвешенные ошибки по бизнес‑показателям для оценки точности прогноза.
Давайте теперь посмотрим на высокую и низкую точность прогнозирования с другой стороны.
Проблема 3. Высокая и низкая точность прогнозирования не является ключевым драйвером экономической эффективности.
Для многих SKU высокая или низкая точность прогнозирования не является ключевым драйвером эффективности.Не стоит рассматривать эти математические ошибки, как что‑то, что всегда нужно использовать для оценки качества управления запасами. Нужно понимать, что эти методы пришли из математики и предназначались именно для статистических и математических, а не экономических показателей.
Например, MAPE использовалась для прогнозирования временных рядов, которые имеют регулярное Нормальное распределение, такие как, например, потребление электроэнергии. И только после ее стали применять для оценки точности прогноза спроса. Но, когда мы говорим про продажи товаров, то Нормальное распределение имеют лишь около 6% товаров. Это, как правило продукты питания ежедневного потребления.
Рассмотрим пример редкого спроса — бытовая химия, которая не востребована каждый день:
Как видно из графика, многие метрики здесь просто не работают. Точность по MAPE и sMAPE невозможно посчитать. Даже, если получиться как‑то ухитриться и «выровнять» данные, то мы получим катастрофически низкую точность — 13%.
Теперь посмотрим на предметную область, а не просто на математические ошибки:
Здесь можно увидеть, что точность прогнозирования вообще ни на что не влияет, потому что остаток обусловлен минимальным квантом поставки или частотой поставки, которую может обеспечивать поставщик. Поэтому обращать внимание на эту цифру совершенно не имеет смысла. И здесь уже стоит заботится не о повышении точности прогнозирования, а о переговорах с поставщиками.
Дефицит в прошлом и высокая точность прогноза
С другой стороны, дефицит в прошлом тоже может вводить в заблуждение относительно точности прогноза. Он занижает продажи, а значит точность может быть завышена или занижена.
В примере, точность по MAPE — 95%. Но при этом мы постоянно попадаем в дефицит, а наш прогноз недооценивает спрос в эти периоды.
Решение 3. Оценивать точность прогнозирования оптимальных запасов и не опираться на математические ошибки
Продолжение в следующей статье.
Дополнительные оборотные средства за счет повышения точности прогноза мы получим, если будем использовать модель прогнозирования, которая дает наименьшую среднюю абсолютную ошибку прогноза.
В данной статье мы рассмотрим:
- Как рассчитать среднюю абсолютную ошибку прогноза и выбрать модель, которая дает наименьшую ошибку;
- Сравним модели и оценим, сколько оборотных средств мы можем сохранить за год, если будем использовать модель, которая дает минимальную ошибку прогноза.
По ходу статьи мы разберем
- Что такое ошибка прогноза;
- Как рассчитывается среднее абсолютное отклонение;
и рассчитаем:
- Прогноз с помощью модели «Скользящей средней к 4-м месяцам с аддитивной сезонностью»;
- Прогноз с помощью модели «Логарифмический тренд с сезонностью»;
- Ошибку прогноза для каждой модели;
- Среднее абсолютное отклонение и для каждой модели.
А также сравним модели, опираясь на среднее абсолютное отклонение и оценим экономию оборотных средств за счет использования более точной модели прогнозирования.
Скачайте файл с примером
Что такое ошибка прогноза?
Ошибкой прогноза продаж является разность между фактическими продажами и прогнозом продаж.
Чем меньше ошибка прогноза, тем более точные решения мы приминаем в закупках, производстве, планировании … а следовательно более эффективно распределяем оборотные средства и повышаем оборачиваемость товаров.
Существует несколько методов оценки ошибок. Большинство этих методов состоит в усреднении некоторых функций от разностей между действительными значениями и их прогнозами.
Ошибку прогноза (et) для каждого момента времени во временном ряду мы можем вычистить по формуле:
et = Yt — Y^t ,
где
- Yt — действительное значение временного ряда в момент t — в наших примерах объем продаж,
- Y^t — прогноз значения Yt — в наших примерах прогноз объема продаж.
Ошибка MAD — среднее абсолютное отклонение
Среднее абсолютное отклонение (MAD) измеряет точность прогноза, усредняя величины ошибок прогноза (абсолютные значения каждой ошибки). Чаще всего MAD используют, когда ошибку прогноза необходимо измерить в тех же единицах, что и исходные значения временного ряда.
Формула вычисления ошибки:
- Yt — действительное значение временного ряда в момент t,
- Y^t — прогноз значения Yt,
- n — номера периодов
Среднее абсолютное отклонение — средняя ошибка (разность между фактом продаж и прогнозом продаж) по модулю.
Рассчитаем прогноз и оценим следующие модели:
- Скользящей средней к 4-м месяцам с аддитивной сезонностью;
- Логарифмический тренд с сезонностью.
Скачайте файл с примером
Для оценки ошибки модели «Скользящей средней к 4-м месяцам с аддитивной сезонностью» рассчитаем:
- Скользящую среднюю к 4-м месяцам;
- Разность между значениями ряда и средними значениями к 4-м месяцам (пункт 1);
- Усредним разность ряда и средней для каждого месяца получим сезонность в абсолютной величание — аддитивную сезонность;
- Продлим значения ряда с помощью скользящей средней к 4-м месяцам и скорректируем её аддитивной сезонностью;
- Модель прогноза для каждого момента времени t;
- Ошибку прогноза;
- Среднее абсолютное отклонение.
1. Скользящую среднюю к 4-м месяцам для каждого момента времени во временном ряду начиная с 5-го периода:
2. Разность между значениями ряда и средними значениями к 4-м месяцам для каждого момента времени t (пункт 1):
3. Усредним разность ряда и средней для каждого месяца получим сезонность в абсолютной величание — аддитивную сезонность.
Для этого вначале выделим номера месяцев с помощью функции Excel =месяц(дата). Для этого проверяем являются ли наши даты «январь 2010 г.», датой, если нет, то переводим в дату и используя функцию Excel =месяц(дата), получаем номера месяцев:
Получаем ряд с пронумерованными месяцами:
Далее усредняем отклонения ряда от средней для каждого месяца, получаем 12 значений аддитивной сезонности.
Для этого используем формулы Excel:
СУММЕСЛИ($D$7:$AY$7 (диапазон с номерами месяцев);D7 (номер месяца, для которого мы рассчитываем сезонность);$D$6:$AY$6 (разность между рядом и средней))
СЧЁТЕСЛИ($D$7:$AY$7(диапазон с номерами месяцев);D7(номер месяца, для которого мы рассчитываем сезонность))
Обязательно фиксируем ссылки на диапазоны с «Номерами месяцев» и «разность между рядом и средней». Подробнее об этом в статье » Как зафиксировать ссылку в Excel»
Подробнее о формулах Excel СУММЕСЛИ и СЧЁТЕСЛИ читайте с статье «Формулы Excel «СУММЕСЛИ» и «СЧЕТЕСЛИ» при расчете сезонности»
Протянули формулу на 12 месяцев, получили аддитивную сезонность для каждого месяца:
4. Продлим значения ряда с помощью скользящей средней к 4-м месяцам и скорректируем её аддитивной сезонностью.
Скорректируем скользящую рассчитанной аддитивной сезонностью.
Для этого к прогнозному среднему прибавим аддитивную сезонность. Сезонность для каждого месяца подтянем с помощью функции Excel ГПР.
Подробнее об этом читайте с статье «ГПР в Excel на примере скользящей средней».
Прогноз = средние продажи за последние 4 месяца + сезонность:
=СРЗНАЧ(AV4:AY4(средние продажи за 4 последних месяца))+ГПР(AZ3 (искомый номер месяца);$D$8:$O$9 (зафиксированная ссылка на таблицу с сезонностью);2 (номер строки);0)
5. Рассчитаем модель прогноза для каждого момента времени t.
К скользящей средней прибавим аддитивную сезонность начиная с 5 периода:
6. Рассчитаем значение ошибки для каждого месяца.
Для этого из объема продаж вычтем значение прогнозной модели:
7. Определим среднее абсолютное отклонение.
Для каждого момента времени t рассчитаем ошибку по модулю с помощью формулы Excel =ABS(H11 (ссылка на ошибку)):
Среднее абсолютное отклонение равно средней ошибке по модулю:
Среднее абсолютное отклонение для модели скользящей средней к 4-м месяцам с аддитивной сезонностью у нас равно 55 475
Теперь рассчитаем прогноз с помощью «Логарифмического тренда с сезонностью».
- Выделим логарифмический тренд;
- Рассчитаем сезонность;
- Рассчитаем значение модели;
- Рассчитаем ошибку прогноза и Среднее абсолютное отклонение.
Скачайте файл с примером
1. Выделим логарифмический тренд.
О всех возможных способах выделения логарифмического тренда в Excel вы можете узнать в нашей статье «5 способов расчета логарифмического тренда в Excel. + О логарифмическом тренде и его применении».
Рассчитаем значения тренда с помощью функции =ПРЕДСКАЗ(LN(D2(номер периода));$D$4:$AY$4 (зафиксированная ссылка на диапазон с объемами продаж);LN($D$2:$AY$2 (зафиксированная ссылка на диапазон с номерами периодов)))
2. Рассчитываем отклонения объемов продаж от тренда (объем продаж делим на значения тренда):
3. Определяем сезонность с помощью формул Excel =СУММЕСЛИ() и =СЧЁТЕСЛИ()
Подробнее о формулах Excel СУММЕСЛИ и СЧЁТЕСЛИ читайте с статье «Формулы Excel «СУММЕСЛИ» и «СЧЕТЕСЛИ» при расчете сезонности»:
Т.к. полученная сезонность в среднем равна 1, то нормирующий коэффициент вводить не нужно, и среднее отклонение у нас будет равно сезонности по месяцам.
4. Определим значения модели прогноза для каждого момента времени t, для этого значения тренда умножим на сезонность. Сезонность подтянем с помощью функции ГПР (см. статью «Функция ГПР в Excel»):
5. Определим ошибку прогноза для каждого момента времени t. Для этого из объема продаж вычтем значение модели прогноза для каждого момента времени t:
6. Рассчитаем ошибку по модулю с помощью функции =ABS(D21″ссылка на ошибку»):
7. Получим среднее абсолютное отклонение по модулю — среднее значение ошибки по модулю:
Среднее абсолютное отклонение для модели «Логарифмического тренда с сезонностью» у нас равно 70 412
Оценим эффективность использования в рамках года одной модели относительно другой.
Среднее абсолютное отклонение для модели
- «Логарифмического тренда с сезонностью» = 70 412 руб.
- «Скользящей средней к 4-м месяцам с аддитивной сезонностью» = 55 475 руб.
Итак модель скользящей средней делает более точный прогноз по сравнение с логарифмическим трендом для этого ряда в месяц на 14 937 руб. = 70 412 руб. — 55 475 руб.
В результате для нас это означает экономию оборотных средств на 14 937 руб. в месяц на обслуживание модели и 179 242 руб. в год, т.е. 14 937 руб. в месяц = 14 937 руб. * 12 месяцев =179 242 руб.
Т.е. в год мы получаем дополнительные оборотные средства в размере 179 242 руб.
Вот так вот за счет оценки точности прогноза и использования модели, которая дает меньшую ошибку прогноза, вы получаете дополнительные оборотные средства — 179 242 руб. в год.
Скачайте файл с примером
Коллеги, эти 2 модели я выбрал наугад, давайте теперь оценим модель, которую автоматически подберет Forecast4AC PRO. И оценим, какой эффект в год нам это даст.
В настройках программы во вкладке «Доп. возможности» ставим галочку «MAD — Среднее абсолютное отклонение» и отключаем модели экспоненциального сглаживания (т.к. они дают ошибку для данного ряда больше чем скользящая средняя и трендовые модели):
Сохраняем и рассчитываем прогноз с помощью Forecast4AC PRO с автоматическим выбором модели.
Автоматически программа выбрала модель Средняя за 2 предыдущих периода + Сезонность относительно средней в абсолютной величине (т.е. аддитивная сезонность). Среднее абсолютное отклонение для этой модели у нас получилось равным 39 882 руб.
|
Экономия оборотных средств модели Forecast4AC PRO относительно модели скользящей к 4-м месяцам в год руб.: |
187 115 руб. |
|
Экономия оборотных средств модели Forecast4AC PRO относительно модели Логарифмический тренд с сезонностью в год руб.: |
366 357 руб. |
Оцените точность моделей прогнозирования, которые вы используете сейчас, рассчитайте проноз с помощью Forecast4AC PRO и оцените сумму оборотных средств, которую вы можете сэкономить за счет использования нашей программы.
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
Когда перед компанией встают задачи прогнозирования спроса для управления товарными запасами, обычно появляется вопрос, связанный с выбором метода прогнозирования. Но как определить, какой метод лучше?
Однозначного ответа на этот вопрос нет. Однако, исходя из нашей практики, самым распространенным методам оценки точности прогноза является средняя абсолютная процентная ошибка (MAPE) . Также используются средняя абсолютная ошибка (MAE) и средняя квадратичная ошибка прогнозирования (RMSE).
Ошибка прогноза в данном случае – это разница между фактическим значением спроса и его прогнозным значением. Т. е, чем больше будет ошибка прогнозирования, тем менее точен прогноз. Например, при ошибке прогнозирования 5%, точность прогноза будет составлять 95%. Изначально MAPE использовалась для прогнозирования временных рядов, которые имеют регулярное нормальное распределение, такие как, например, потребление электроэнергии. И только после ее стали применять для оценки прогноза спроса. На практике ошибку могут рассчитывать по каждой позиции товара, а также среднюю оценку по всем товарным группам.
Несмотря на то, что большинство компаний до сих пор используют вышеописанные методы для оценки, мы считаем, что они не достаточно корректны и не подходят для применения в реальном бизнесе. Для простоты изложения, выделим три ключевых момента, которые приводят к некорректным выводам при использовании вышеописанных методов оценки. Назовем их ошибка № 1, № 2 и № 3. Сначала мы подробно опишем эти ошибки, а потом расскажем, как наши методы сравнения помогаю их ликвидировать.
О некорректности использования MAPE, RMSE и других распространенных ошибок
Ошибка № 1 заключается в том, что используемые методы больше относятся к математике, нежели к бизнесу, по той причине, что это обезличенные цифры (или проценты) , которые ничего не говорят про деньги. Бизнесу же нужно принимать решения на основе выгоды, которую он получит в деньгах. Например, ошибка в 80% на первый взгляд звучит устрашающие. Но в реальности за ней могут скрываться совершенно разные вещи. Ошибка по гвоздям со стоимостью одного гвоздя в 0,5 рублей – это одни потери. Но они совершенно несопоставимы с потерями от продажи промышленного оборудования стоимостью 700 000 рублей с той же величиной ошибки прогнозирования. Ко всему прочему также больше значение имеет объем продукции, что тоже никак не учитывается данными ошибками прогнозирования.
Второй важный момент (ошибка №2), который не учитывают данные оценки прогнозирования – это заморозка денежных средств в запасах и недополученная прибыль от дефицита продукции на складе. Например, если мы прогнозируем продажу 20 колесных дисков, а по факту продали 15. То это одна цена ошибки – 5 колесных дисков, которые потребуют затраты на хранение на определенное время, и как следствие стоимость замороженных оборотных средств под определенный процент. Если рассмотреть обратную ситуацию – прогнозируем продажу 20 дисков, спрос составляет 25 штук. Это уже упущенная прибыль, которая составляет разницу сумм закупки и реализации продукции. По сути мы имеет одну и ту же ошибку прогнозирования, но результат от нее может быть совершенно разным.
Третий ключевой момент (ошибка №3) – описанные ошибки распространяются только на точечный прогноз спроса и не описывают страховой запас. А он в некоторых случаях может составлять от 20% до 70% от общих товарных запасов на складе. Поэтому, какой бы точный не был прогноз с точки зрения описанных выше методов, мы все равно не оцениваем точность страхового запаса, а значит реальные данные могут быть значительно искажены.
Критерии, привязанные к прибыльности бизнеса
Учитывая описанные выше недостатки ошибок прогнозирования, такой подход не является корректным и надежным для сравнения алгоритмов. Ко всему прочему он зачастую оторван от реального бизнеса. Используемый же нами подход позволяет оценить точность алгоритмов в деньгах, рассчитать стоимость ошибки прогнозирования на понятном для бизнеса языке финансов. Таким образом это позволяет нам ликвидировать ошибку №1.
В случае с ошибкой № 2, мы рассчитываем два различных значения. Если прогноз окажется меньше реального спроса, то он приведет к дефициту, экономический урон от которого рассчитывается, как количество недопроданных товаров, умноженное на разность цен закупки и реализации. Например, вы закупаете колесные диски по 3000 рублей за штуку и продаете по 4000. Прогноз на месяц составил 1000 дисков, реальный спрос оказался 1200 штук. Экономический урон будет равен:
(1200-1000)*(4000-3000)=200 000 рублей.
В случае превышения прогноза над реальным спросом компания понесет убытки по хранению продукции. Экономический урон будет равен сумме затрат на нереализованную продукцию, помноженную на ставку альтернативных вложений за этот период. Предположим, что реальный спрос в предыдущем примере оказался 800 дисков и вам пришлось хранить диски еще один месяц. Пусть ставка альтернативных вложений составляет 20% в год. Тогда экономический урон будет равен
(1000-800)*3000*0,2/12=10 000 рублей.
Соответственно, в каждом конкретном случае, мы будет учитывать одно из этих значений.
Для того, чтобы ликвидировать ошибку № 3, мы сравниваем алгоритмы с использованием понятия уровень сервиса. Уровень сервиса (здесь и далее — уровень сервиса II рода, fill rate) – это доля спроса, которую мы гарантировано покроем с использованием имеющихся на складе запасов в течении периода их пополнения. Например, уровень сервиса 90% означает, что мы удовлетворим 90% спроса. На первый взгляд может показаться логичным, что уровень сервиса всегда должен составлять 100%. Тогда и прибыль будет максимальна. Но в реальных ситуациях зачастую дело обстоит иначе: удовлетворение 100% уровня сервиса приводит к сильному перезатариванию склада, а для товаров с ограниченными сроками годности еще и к списанию. И убытки от затрат на хранение, списания просроченной продукции и недополученной прибыли от вложения свободных денег в итоге снизят прибыть от реализации, в случае если бы мы поддерживали уровень сервиса 95%. Нужно заметить, что для каждой отдельной позиции товаров будет свой оптимальный уровень сервиса.
Так как страховой запас может составлять значительную долю, его нельзя игнорировать при сравнении алгоритмов (как это делается при расчете ошибок MAPE, RMSE и т. д.) . Поэтому мы делаем сравнение не прогноза, а оптимального запаса с заданным уровнем сервиса. Оптимальный запас для заданного уровня сервиса – это такое количество товаров, которое нужно хранить на складе, чтобы получить максимум прибыли от реализации товаров и одновременно сократить издержки на хранение до минимума.
В качестве основного критерия (критерий №1) качества прогнозирования мы используем суммарное значение потерь для заданного уровня сервиса, о котором писали выше (исправление ошибки №2). Таким образом мы оцениваем потери в денежном выражении при использовании данного конкретного алгоритма. Чем меньше потери — тем точнее работает алгоритм.
Здесь нужно заметить, что для разных уровней сервиса оптимальный запас тоже может различаться. И в одном случае прогноз будет точно в него попадать, а в другом возможны перекосы в большую, либо меньшую сторону. Так как многие компании не рассчитывают оптимальный уровень сервиса, а используют заданный заранее, значение основного критерия мы вычисляем для всех самых распространенных уровней сервиса: 70%, 75%, 80%, 85%, 90%, 95%, 98%, 99% и суммируем потери. Таким образом мы можем проверить, насколько хорошо в целом работает модель.
Для компаний, которые, считают оптимальный уровень сервиса мы используем дополнительный критерий (критерий №2) для оценки. В общем виде он выглядит как соотношение потерь на оптимальном уровне сервиса по ожидаемому (модельному) распределению продаж и по реальному распределению продаж (по факту) . Прогнозируемое значение оптимального уровня сервиса не всегда соответствует оптимальному значению уже на реальном распределении продаж. Поэтому мы должны сравнивать ошибку между прогнозом объема продаж на оптимальном (по модели) уровне сервиса и реальным объемом продаж, обеспечивающим оптимальное значение уровня сервиса по реальным данным.
Что проиллюстрировать применение данного критерия, вернемся к нашему примеру с дисками. Предположим, что прогнозное значение оптимального уровня сервиса для него составляет 90%, а оптимальный объем запаса для этого случая примем равным 3000 колесных дисков. Пусть в первом случае реальный уровень сервиса оказался выше прогнозного и составил 92%. Соответственно объем заказов также вырос и составил 3300 дисков. Ошибка прогнозирования будет рассчитываться как разность между реальным и фактическим объемом продаж, умноженная на разность цен реализации. Итого, мы имеем:
(3300-3000)*(4000-3000)=300 000 рублей.
Теперь представим обратную ситуацию: реальный уровень сервиса оказался меньше прогнозного и составил 87%. Реальный объем продаж при этом составил 2850 дисков. Ошибка прогнозирования будет рассчитана, как сумма затрат на нереализованную продукцию, умноженную на ставку альтернативных вложений за этот период (в качестве примера берем период сроком месяц и ставку равную 20% годовых) . Итоговое значение критерия будет равно:
(3000-2850)*3000*0,2/12 = 7500 рублей
Конечно, в идеальном случае, мы должны рассчитывать ошибку только при оптимальном уровне сервиса, между прогнозным и реальным значениями. Но так как не все компании еще перешли на оптимальный уровень сервиса, мы вынуждены использовать два критерия.
Используемые нами критерии в отличие от классических математических ошибок, показывают суммарные потери в деньгах при применении той или иной модели. Соответственно, наилучшей будет модель, которая обеспечивает минимальные потери. Такой подход позволят бизнес-пользователям оценить работу различных алгоритмов на понятном им языке.
Пример сравнения точности прогнозирования системы Forecast NOW c методом ARIMA (на базе номенклатуры бытовой химии) :
Пример сравнения точности прогнозирования системы Forecast NOW c методом Кростона (на базе номенклатуры бытовой химии) :
Насколько корректно на ваш взгляд считать ошибки, а не деньги? Предлагаем порассуждать на эту тему в комментариях!
Ошибка прогнозирования: виды, формулы, примеры
Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.
В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):
Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!
MPE — Mean Percent Error
MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.
- Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
- Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
- Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error
MAPE — Mean Absolute Percent Error
MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
- Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
- Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error
Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.
WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error
WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
- Находится сумма всех фактов по всем позициям (общий фактический объем)
- Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE
Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.
Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.
RMSE (as %) / nRMSE — Root Mean Square Error
RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.
- Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
- Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
- Извлекаем корень из полученного результат — RMSE
- Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
- Разделить на разницу между максимальным и минимальным значением показателей
- Разделить на разницу между третьим и первым квартилем значений показателей
- Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)
MASE — Mean Absolute Scaled Error
MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.
Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.
Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:
Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.
Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.
Об авторе
HeinzBr
Автор статей и создатель сайта SHTEM.RU
Для анализа результатов расчета прогноза, в продолжение ряда вы можете рассчитать следующие ошибки:
- MAPE – средняя абсолютная ошибка в % . Ошибка оценивает на сколько велики ошибки в сравнении со значением ряда и с ошибками в соседних рядах.
Подробнее читайте в статье на нашем сайте: http://4analytics.ru/metodi-analiza/mape-%E2%80%93-srednyaya-absolyutnaya-oshibka-praktika-primeneniya.html - MRPE – средняя относительная ошибка в %, оценивает на сколько велика дельта между фактом и прогнозом. Чем ближе к 100%, тем больше ошибка, чем ближе к нулю, тем ошибка меньше.
- MSE – средняя квадратическая ошибка, подчеркивает большие ошибки за счет возведения каждой ошибки в квадрат.
Подробнее читайте в статье на нашем сайте:
http://4analytics.ru/metodi-analiza/mse-%E2%80%93-srednekvadraticheskaya-oshibka-v-excel.html - MPE – средняя процентная ошибка – показывает завышен или занижен прогноз относительно факта. Если ошибка меньше нулю, то прогноз последовательно завышен, если ошибка больше нуля, то прогноз последовательно занижен.
Подробнее читайте в статье на нашем сайте:
http://4analytics.ru/metodi-analiza/mpe-%E2%80%93-srednyaya-procentnaya-oshibka-v-excel.html - MAD – среднее абсолютное отклонение. Используется, когда важно измерить ошибку в тех же единицах, что и исходный ряд.
Подробнее читайте в статье на нашем сайте:
http://4analytics.ru/planirovanie-i-prognozirovanie-praktika/dopolnitelnie-oborotnie-sredstva-za-schet-povisheniya-tochnosti-prognoza.html - A MAPE – ошибка, которая показывает отклонение средних значений ряда к средним значениям модели прогноза. Имеет значение при неравномерном перераспределении значений ряда по периодам.
- S MAPE – ошибка, которая показывает отклонение суммы значения ряда к сумме значений модели прогноза. Имеет значение при неравномерном перераспределении значений ряда по периодам.
А также 2 показателя «Точность прогноза»:
- Точность прогноза = 1 – МАРЕ
- Точность прогноза 2 = 1 – MRPE
Для расчета ошибок одновременно с прогнозом, нажимаем кнопку «Расчет ошибок» в меню «FORECAST»
В открывшемся окне выбираем нужные для расчета ошибки:
Теперь при расчете прогноза, в продолжение ряда, программа автоматически сделает расчет отмеченных Вами ошибок: