В последние
десятилетия в мире усиленно развивается
новая прикладная область математики,
специализирующаяся на нейронных сетях
(НС) [10]. Нервная система и мозг человека
состоят из нейронов, соединенных между
собой нервными волокнами. Нервные
волокна способны передавать электрические
импульсы между нейронами. Все процессы
передачи раздражений от нашей кожи,
ушей и глаз к мозгу, процессы мышления
и управления действиями – все это
реализовано в живом организме как
передача электрических импульсов между
нейронами.
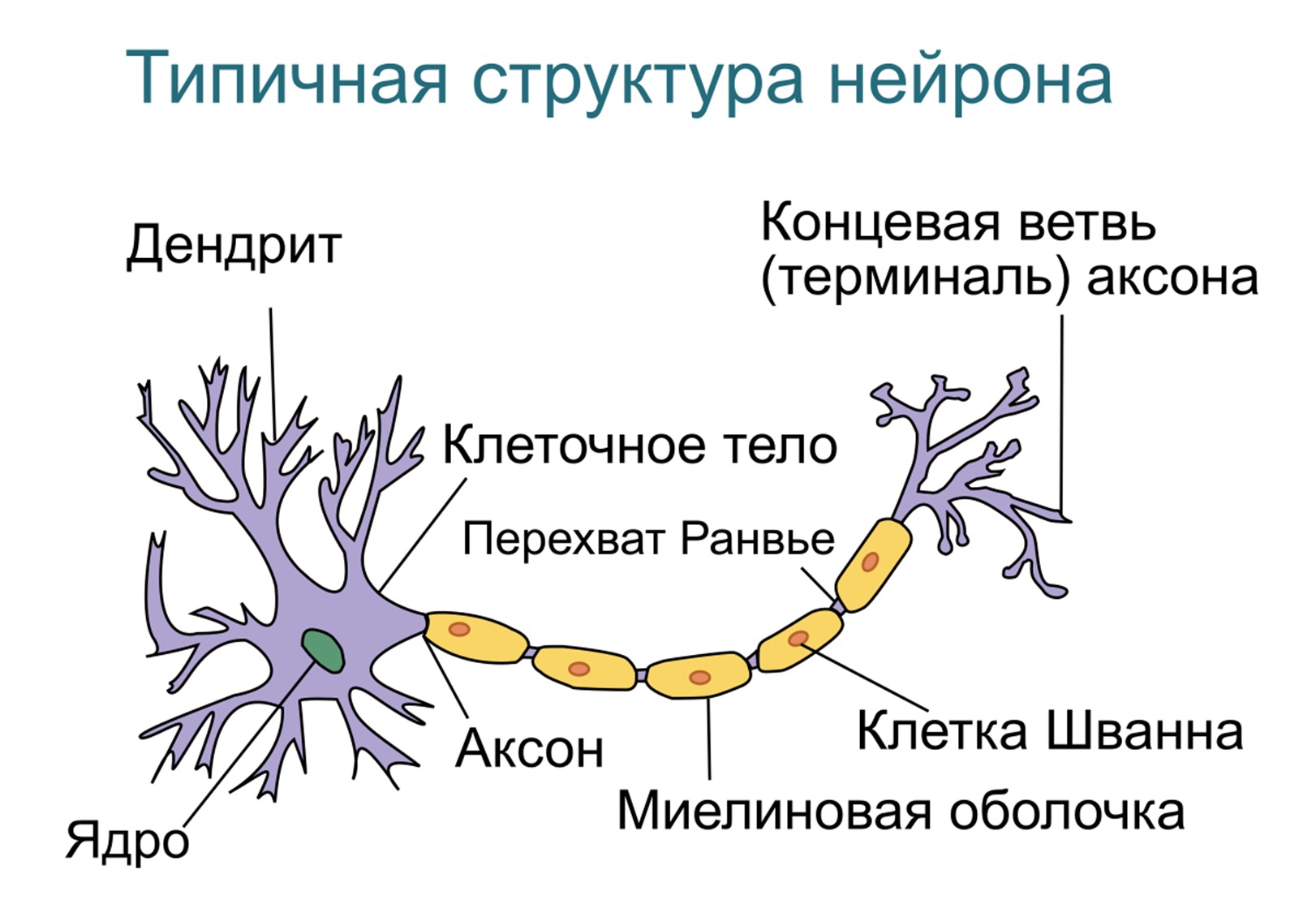
Рассмотрим строение
биологического нейрона. Каждый нейрон
имеет отростки нервных волокон двух
типов – дендриты, по которым принимаются
импульсы, и единственный аксон, по
которому нейрон может передавать
импульс. Аксон контактирует с дендритами
других нейронов через специальные
образования – синапсы, которые влияют
на силу импульса.
Рис.
5.5.1. Строение биологического нейрона
Можно считать, что
при прохождении синапса сила импульса
меняется в определенное число раз,
которое мы будем называть весом синапса.
Импульсы, поступившие к нейрону
одновременно по нескольким дендритам,
суммируются. Если суммарный импульс
превышает некоторый порог, нейрон
возбуждается, формирует собственный
импульс и передает его далее по аксону.
Важно отметить, что веса синапсов могут
изменяться со временем, а значит, меняется
и поведение соответствующего нейрона.
Можно построить
математическую модель описанного
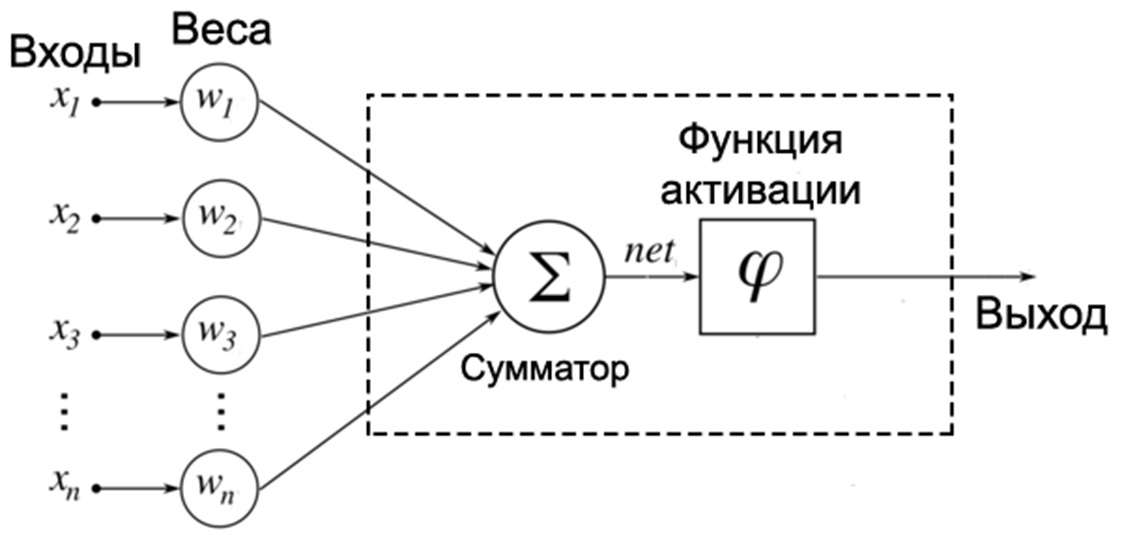
процесса. На рисунке 5.5.2 изображена
модель нейрона с тремя входами
(дендритами), причем синапсы этих
дендритов имеют веса w1,
w2,
w3.
Пусть к синапсам поступают импульсы
силы x1,
x2,
x3
соответственно, тогда после прохождения
синапсов и дендритов к нейрону поступают
импульсы w1x1,
w2x2,
w3x3.
Нейрон преобразует полученный суммарный
импульс x=w1x1+w2x2+w3x3
в соответствии с некоторой передаточной
функцией f(x).
Сила выходного импульса равна
y=f(x)=f(w1x1+w2x2+w3x3).
Таким образом, нейрон полностью
описывается своими весами wi
,
и передаточной функциейf(x).
Получив набор чисел (вектор) xi
на вход, нейрон выдает некоторое число
y
на выходе, являющееся функцией от входных
сигналов.
Рис. 5.5.2. Модель
искусственного нейрона с тремя входами
и одним выходом
Искусственной
нейронной сетью называют некоторое
устройство или его программную реализацию,
которое состоит из большого количества
параллельно работающих процессорных
элементов – нейронов, соединенных
адаптивными линиями передачи информации
– связями или синапсами.
Некоторые входы
нейронов помечены как внешние входы
сети, а некоторые выходы – как внешние
выходы сети. Подавая любые числа на
входы сети, мы получаем какой-то набор
чисел на выходах сети. Таким образом,
работа нейросети состоит в преобразовании
входного вектора в выходной вектор,
причем это преобразование задается
весами сети.
Теперь, когда стало
ясно, что именно мы хотим построить, мы
можем переходить к вопросу «как строить
такую сеть». Этот вопрос решается в два
этапа:
-
Выбор типа
(архитектуры) сети. -
Подбор весов
(обучение) сети.
На первом этапе
следует определить, какие нейроны мы
хотим использовать (число входов,
передаточные функции), каким образом
следует соединить их между собой, что
взять в качестве входов и выходов сети.
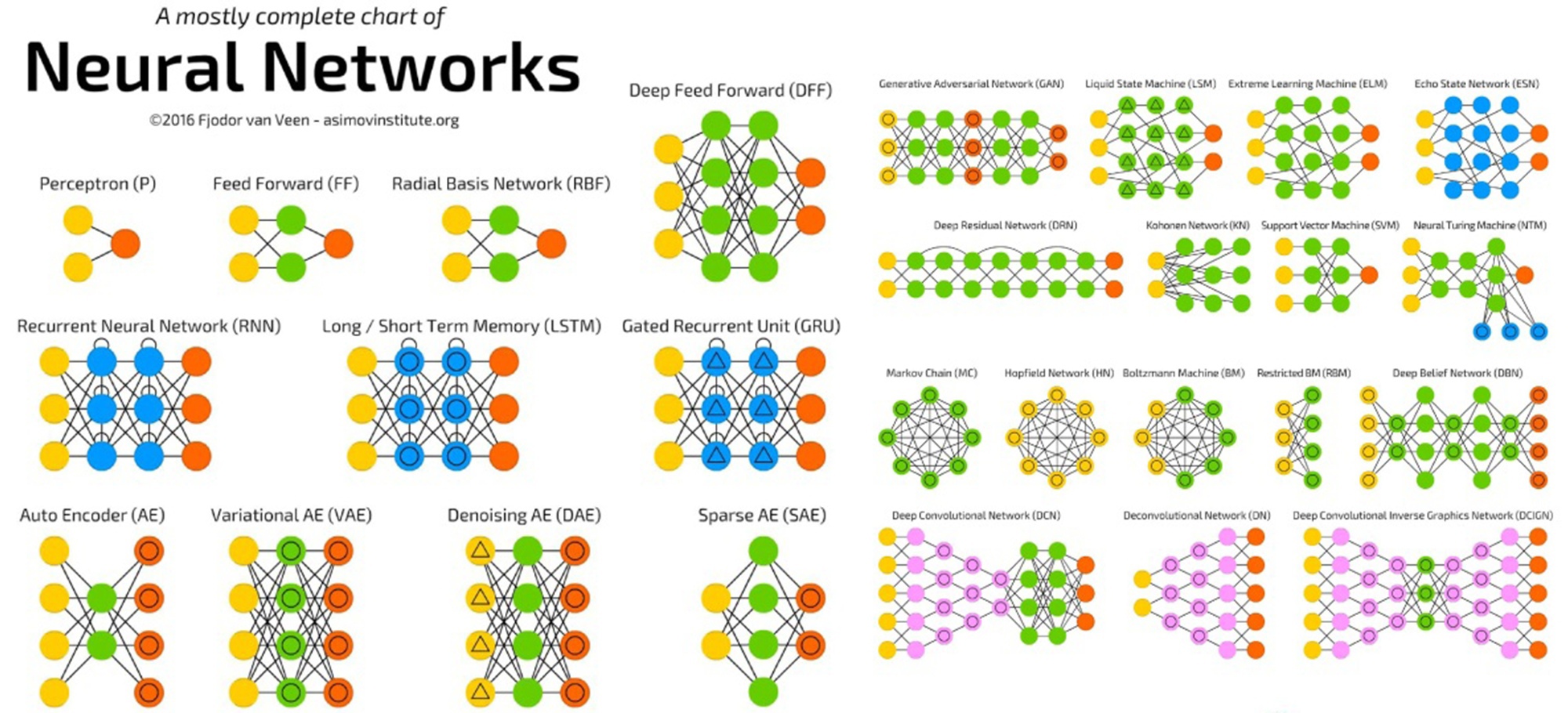
Эта задача на
первый взгляд кажется весьма сложной,
но она упрощается, т.к. нам необязательно
придумывать нейросеть с нуля – существует
несколько десятков различных нейросетевых
архитектур, причем эффективность многих
из них доказана математически [10]. В
данной работе использован наиболее
популярный и свободно распространяемый
по сети Интернет программный продукт
Neuro
Pro,
представляющий собой менеджер обучаемых
искусственных нейронных сетей, работающий
в среде MS
Windows
XP.
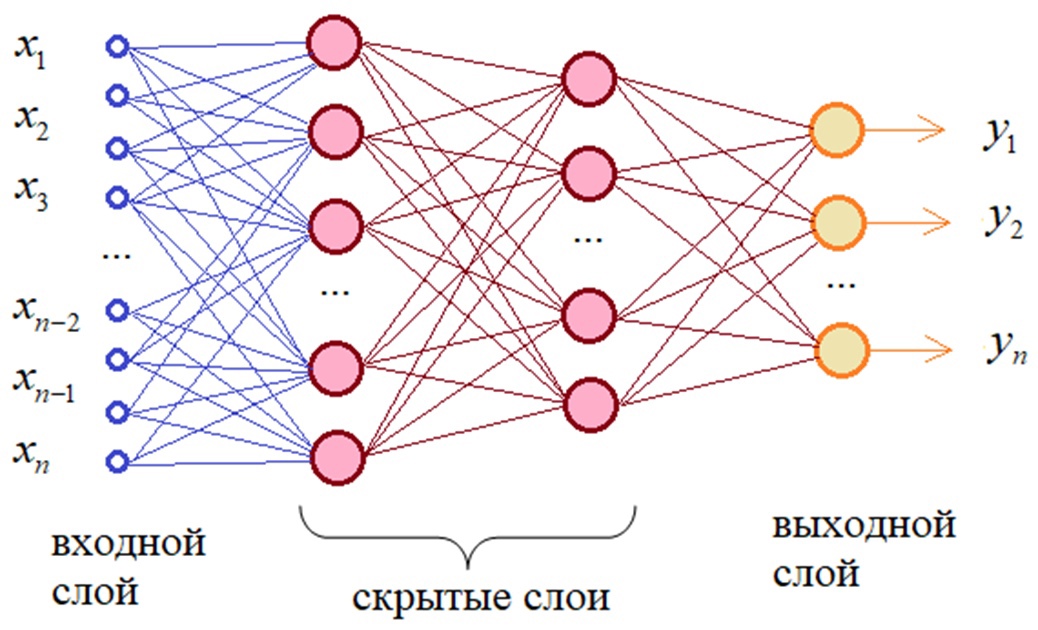
Для решения
поставленной задачи наиболее подходит
многослойная нейронная сеть с
последовательными связями, в которой
нейроны объединяются в слои. Слой
содержит совокупность нейронов с едиными
входными сигналами. Число нейронов в
слое может быть любым и не зависит от
количества нейронов в других слоях.
Внешние входные сигналы подаются на
входы нейронов входного слоя, а выходами
сети являются выходные сигналы последнего
слоя. Кроме входного и выходного слоев
в многослойной нейронной сети есть один
или несколько скрытых (внутренних)
слоев.
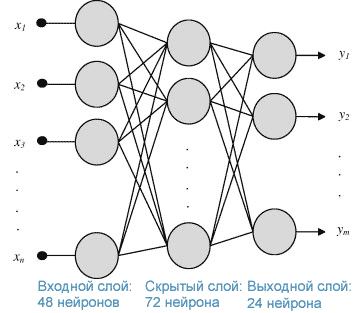
-
Количество нейронов
во входном слое будем менять: 3, 4, 6, 8,
т.к. для прогнозирования будем использовать
три, четыре, шесть или восемь последних
значений. -
Количество выходов
(выходной слой) = 1, значение переменной,
следующей за последними тремя, четырьмя,
шестью, восемью значениями. -
Количество нейронов
внутреннего слоя. Для более точной
аппроксимации и лучшей сходимости ряда
возьмем количество скрытых слоев,
равное 3, а количество нейронов в каждом
из скрытых слоев равное 10 [10].
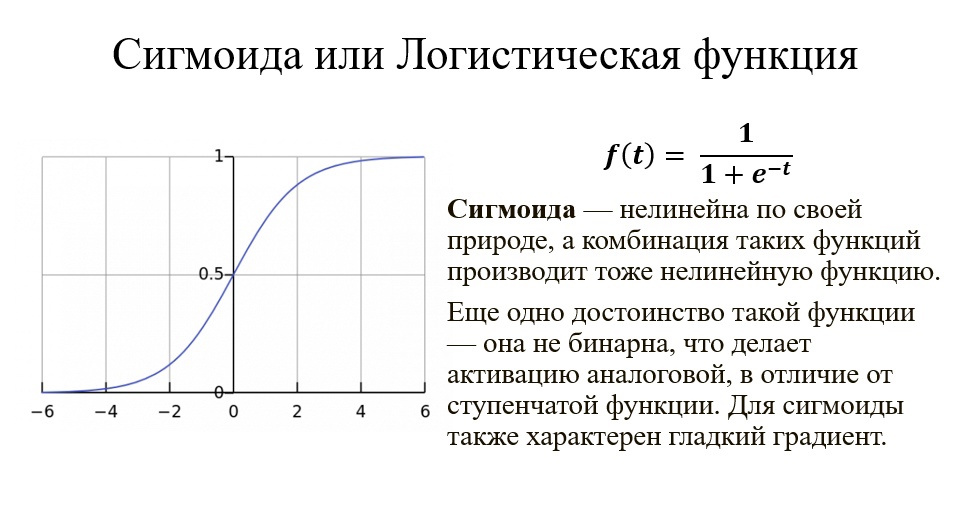
В качестве
активационной функции нейронов скрытых
слоев возьмем наиболее часто используемый
на практике сигмоид [10], который имеет
следующий вид:
. (5.5.1)
Основное достоинство
этой функции в том, что она дифференцируема
на всей оси абсцисс и имеет сравнительно
простую производную:
f‘(x)=a*f(x)(1-f(x)).(5.5.2)
Кроме того, она
обладает свойство усиливать слабые
сигналы лучше, чем большие, и предотвращать
насыщение от больших сигналов, т.к. они
соответствуют областям аргументов, где
сигмоид имеет пологий наклон.
На втором этапе
нам следует «обучить» выбранную сеть
– значит сообщить ей, чего мы от нее
добиваемся. Схематично процесс обучения
нейросети представлен на рис 5.5.3.
Рис. 5.5.3. Процесс
обучения нейросети
После многократной
подачи на вход нейросети обучающих
примеров передаточные веса сети
стабилизируются, причем сеть дает
правильные ответы на все (или почти на
все) подаваемые примеры. В таком случае
говорят, что «сеть выучила все примеры»,
«сеть обучена» или «сеть натренирована»
[10]. В программных реализациях можно
видеть, что в процессе обучения величина
ошибки (сумма квадратов ошибок по всем
выходам) постепенно уменьшается. Когда
величина ошибки достигает нуля или
приемлемого малого уровня, тренировку
(обучение) заканчивают, а полученную
сеть считают натренированной (обученной)
и готовой к применению на готовых новых
данных.
Важно отметить,
что вся информация, которую сеть имеет
о задаче, содержится в наборе примеров.
Поэтому качество обучения сети напрямую
зависит от количества примеров в
обучающей выборке, а также от того,
насколько полно эти примеры описывают
данную задачу.
Объем обучающей
выборки зависит от выбранного нами
количества входов. Если в качестве
входного сигнала взять 20 элементов ВДР,
то такая сеть потенциально могла бы
строить лучший прогноз, чем сеть с 4
элементами на входе, однако в этом случае
мы имеем всего 1 обучающий пример, и
обучение скорее всего не даст приемлемого
результата. При выборе числа элементов
на входе следует учитывать это, выбирая
разумный компромисс между глубиной
предсказания (число элементов на входе)
и количеством обучающих тестов.
В данной работе с
целью уменьшения ошибки прогноза была
сделана попытка изменения количества
входов нейронной сети, которому
последовательно присваивались значения
3, 4, 6 и 8.
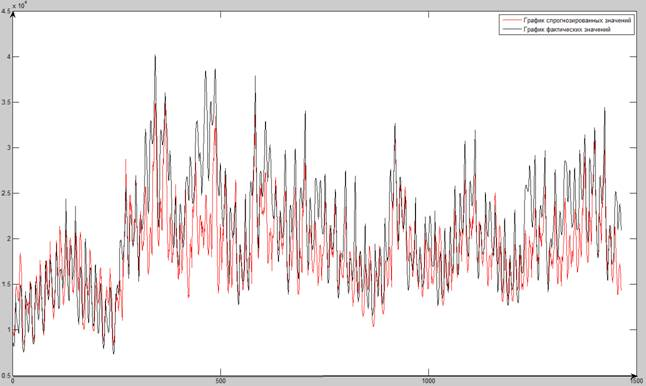
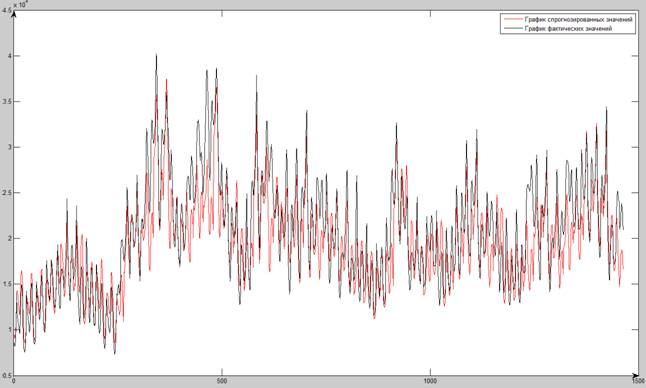
Прогнозируемые
значения, полученные методом прогнозирования
в нейронных сетях, представлены в
таблицах 49 – 62 приложения 1.
Сводные результаты
сглаживания и прогнозирования на
нейронных сетях при изменении количества
элементов ВДР на входе приведены в
таблице 5.5.1.
По результатам
таблицы 5.5.1 были сделаны следующие
основные выводы:
-
Изменение количества
элементов ВДР на входе нейронной сети
(3; 4; 6;при прогнозировании на нейронных
сетях показало, что наиболее близкие
к фактическим значениям прогнозируемые
значения в большинстве случаев достигают
при количестве элементов ВДР на входе,
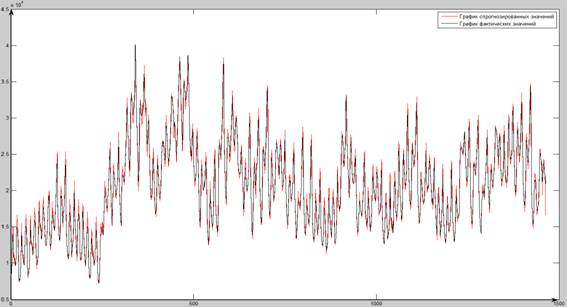
равное 8. -
Наименьшая ошибка
прогнозирования методом прогнозирования
на нейронной сети составила 0,024973516, а
наибольшая – 0,822503966. -
Наиболее достоверные
результаты, полученные при прогнози-
ровании на нейронных сетях, представлены
в таблице 5.5.2.
Таблица 5.5.1
УДК 004.832.22, 681.324:612.82, 681.3.07
Т.В. Любимова
старший преподаватель Кафедра «Экономические и естественно-научные дисциплины» Северо-кавказский филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Белгородский государственный технологический
университет им. В.Г. Шухова» г. Минеральные Воды, Российская Федерация
А.В. Горелова Преподаватель
Кафедра «Экономические и естественно-научные дисциплины» Северо-кавказский филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Белгородский государственный технологический
университет им. В.Г. Шухова» г. Минеральные Воды, Российская Федерация
РЕШЕНИЕ ЗАДАЧИ ПРОГНОЗИРОВАНИЯ С ПОМОЩЬЮ НЕЙРОННЫХ СЕТЕЙ
Аннотация
В статье рассматривается вопрос применения нейронных сетей для задачи прогнозирования временного ряда. Построен алгоритм прогнозирования и описано решение данной задачи. Показан общий принцип работы нейронных сетей и дана точность прогноза.
Ключевые слова
Нейронная сеть, прогнозирование, временной ряд, аппроксимация функции, точность прогноза,
ошибка прогнозирования.
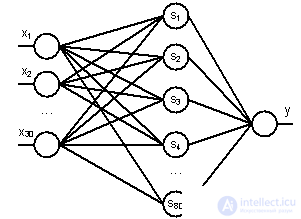
Нейронные сети возникли из исследований в области искусственного интеллекта, а именно, из попыток воспроизвести способность биологических нервных систем обучаться и исправлять ошибки, моделируя низкоуровневую структуру мозга. Структурной единицей, из которой состоит любая нейронная сеть, является нейрон. Нейроны соединены между собой с помощью синапсов. Входами одного нейрона являются выходы другого. Это продемонстрировано на рисунке 1.
Ьхпдаой слой I Ьнутрошай свай Ллг/тргшжА икА Вшадной слой
Рисунок 1 — Искусственная нейронная сеть Основной принцип работы нейронной сети состоит в настройке параметров нейрона таким образом, чтобы поведение сети соответствовало некоторому желаемому поведению. На рисунке 2 показана общая структура обучения нейронной сети.
Входы Синапсы
Рисунок 2 — Общая структура обучения нейронной сети
Способности нейронной сети к прогнозированию напрямую следуют из ее способности к обобщению и выделению скрытых зависимостей между входными и выходными данными. После обучения сеть способна предсказать будущее значение некой последовательности на основе нескольких предыдущих значений или каких-то существующих в настоящий момент факторов. Следует отметить, что прогнозирование возможно только тогда, когда предыдущие изменения действительно в какой-то степени предопределяют будущие.
Нейронные сети — это мощный и гибкий механизм прогнозирования. При определении того, что нужно прогнозировать, необходимо указывать переменные, которые анализируются и предсказываются. Здесь очень важен требуемый уровень детализации. На используемый уровень детализации влияет множество факторов: доступность и точность данных, стоимость анализа и предпочтения пользователей результатов прогнозирования.
Точность прогноза, которая требуется для конкретной проблемы, оказывает огромное влияние на прогнозирующую систему. Также огромное влияние на прогноз оказывает обучающая выборка.
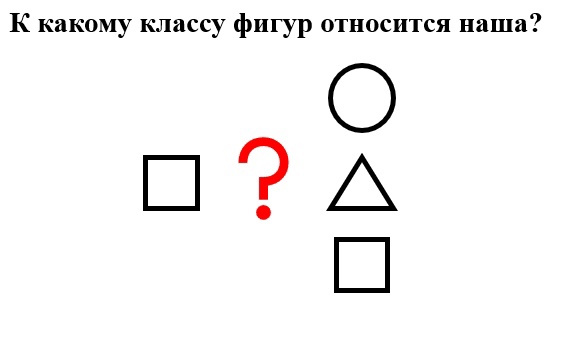
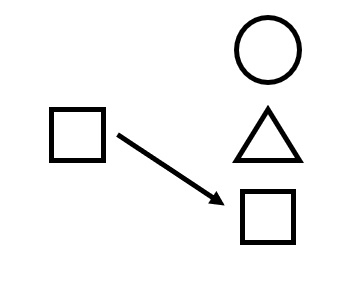
Одной из актуальных задач, при решении которой используют нейронные сети, является задача прогнозирования временного ряда. Временной ряд — совокупность значений какого-либо показателя за определенное количество последовательных моментов или периодов времени. Прогнозирование является чрезвычайно трудной задачей, поскольку традиционная архитектура НС и методы формирования обучающей выборки для них не совсем подходят для распознавания образов, которые изменяются с течением времени. Изначально НС предназначались для распознавания структурных образов. В таких задачах сети демонстрируется образ, состоящий из набора визуальных, семантических или других свойств, и сеть должна распознать входной образ, как принадлежащий одному или нескольким классам. При прогнозировании временного ряда обрабатываются образы, которые изменяются с течением времени и поэтому трудно сказать, что сеть обладает полной информацией.
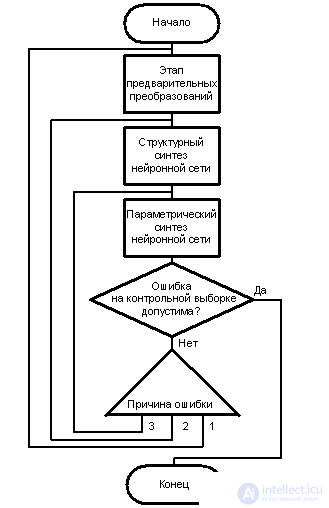
Схему решения задачи прогнозирования можно представить в виде последовательности этапов (рисунок 3) [1, с 32].
Рисунок 3 — Схема решения задачи прогнозирования Для решения задач прогнозирования с помощью нейронных сетей в настоящее время применяют подход аппроксимации функции. Во многих работах по теории и применению нейронных сетей имеет место утверждение, что нейронные сети являются одним из лучших методов аппроксимации функций [2, с.296]. В результате обучения настраиваемые параметры сети принимают вид, соответствующий некоторой функции представленной входными и выходными векторами обучающего множества, используя подход аппроксимации функции [3]. Данный подход применяется в задачах прогнозирования, в которых каждому конкретному входному вектору, представленному входными параметрами нейронной сети, соответствует конкретное значение прогнозируемого вектора, представленного выходными параметрами нейронной сети:
У,=/(х,) (1)
где Xi — i — й входной вектор;
у — соответствующее значение прогнозируемого вектора; / (хг) — прогнозирующая функция.
Отрицательный результат обучения возможен из-за сложной формы аппроксимируемой функции в условиях неполных данных, необходимых для успешной аппроксимации функции. При вводе в систему некоторой допустимой погрешности обучения, мы можем избежать подобных результатов.
Задача прогнозирования временных рядов является одной из классических задач, эффективно решаемых с помощью нейронных сетей. Способность нейронных сетей после обучения к обобщению и экстраполяции результатов создает потенциальные предпосылки на их базе различного рода прогнозирующих систем.
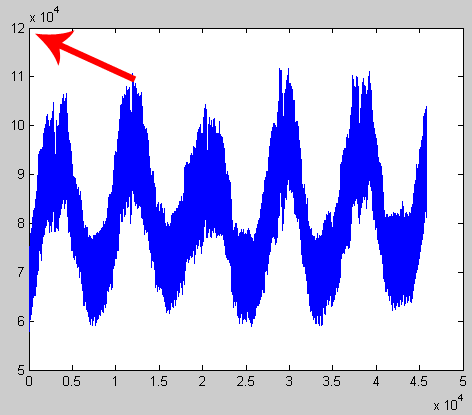
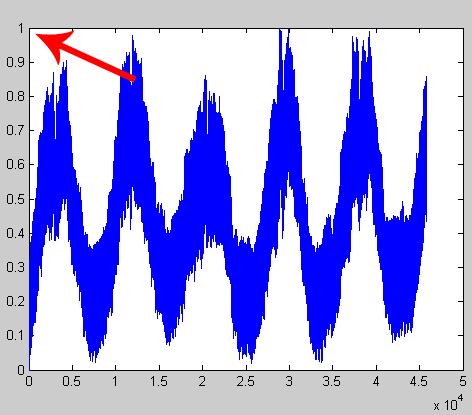
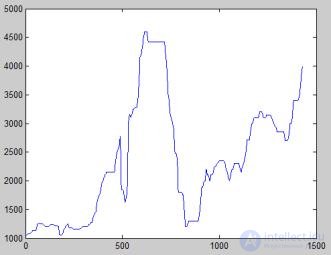
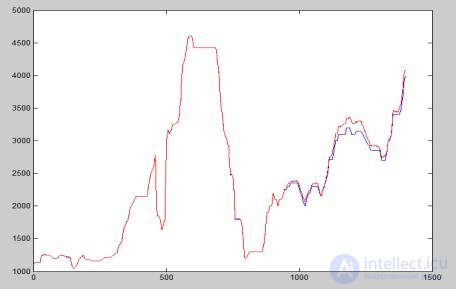
Рассмотрим временной ряд хф на промежутке I = 1, т. Тогда суть задачи прогнозирования состоит в том, чтобы найти продолжение временного ряда на неизвестном промежутке, то есть необходимо определить х(т+1 ),х(т + 2) и т.д. (рисунок 4).
Рисунок 4. Иллюстрация задачи прогноза с помощью нейронных сетей Совокупность известных значений временного ряда образует обучающую выборку, размерность которой характеризуется значением т. Для прогнозирования временных рядов используется метод «скользящего окна». Он характеризуется длиной окна р, равной числу элементов ряда, одновременно подаваемых на нейронную сеть. Данное положение определяет структуру нейронной сети, которая включает в себя р распределенных нейронов и один выходной нейрон.
Построенная модель скользящего окна для нейронных сетей с линейной функцией активации соответствует линейной авторегрессии и описывается выражением:
x(n) = ^ wk ■ x(n — p + k -1)
(2)
k=i
где ~№к,к = 1,р — весовые коэффициенты нейронной сети;
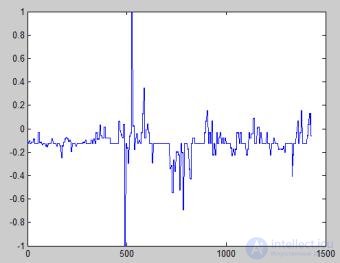
х (п) — оценка значения ряда х(п) в момент времени п. Ошибка прогнозирования определяется выражением:
е(п) = х(п) — х(п)
(3)
Модель линейной авторегрессии формирует значение ряда х(п), как взвешенную сумму предыдущих значений ряда. Обучающая выборка нейронной сети представляется в виде матрицы, строки которой характеризуют векторы, подаваемые на вход нейронной сети:
х(1) х(2) … х( р)
х(2) х(3) … х( р +1)
X =
x(m — p) x(m -1 +1)
x(m -1)
(4)
Это эквивалентно перемещению окна по ряду х(0 с единичным шагом.
Таким образом, выборка известных членов ряда используется для обучения нейронной сети прогнозированию. После обучения сеть должна прогнозировать временной ряд на упреждающий промежуток времени.
Международный научный журнал «ИННОВАЦИОННАЯ НАУКА»_ISSN 2410-6070_№ 4/2015
Точность прогноза
Точность прогноза, требуемая для решения конкретной задачи, оказывает большое влияние на прогнозирующую систему. Ошибка прогноза зависит от используемой системы прогноза. Чем больше ресурсов имеет такая система, тем больше шансов получить более точный прогноз. При прогнозировании всегда учитывается возможная ошибка прогнозирования [3, с.45]. Точность прогноза характеризуется ошибкой прогноза.
Часто берется абсолютное отклонение прогноза Ъ 0 от истинного значения деленное на истинное значение: ь, , i
d’ = ^^ (5)
Ъг0
Такая относительная величина мало чувствительна к ошибкам прогноза больших значений и чрезмерно чувствительна к ошибкам прогноза величин, близких к нулю. Кроме того, разница ddi между минимальным и максимальным значениями может быть различной у разных наблюдаемых характеристик и одинаковая относительная ошибка d’ будет приемлемой для принятия решений в одних случаях и не приемлемой в других.
В связи с этим предлагается судить о точности прогноза i -й характеристики по величине ошибки, нормированной по разнице dd :
. ~bi,0
d = —1 (6)
ddi
Такая мера обладает одинаковой чувствительностью к ошибкам прогноза для разных значений прогнозируемой характеристики. Ее чувствительность к ошибкам тем выше, чем в меньших пределах колеблется прогнозируемая характеристика, что представляется вполне логичным.
Иногда важно знать не абсолютную величину характеристики в будущем, а лишь то, будет ли она больше или меньше значения в данный момент времени. В таких случаях применима мера точности прогноза, учитывающая лишь совпадения знаков:
о , если ъо > Ъ,) и Ф: о > ъi,,)
или Ъо < ,) и Ъо < ); (7)
0.5, есш (Ъ,.,о = Ъ„) и (Ъ’ио * bi,t);
1, в других случаях
Вывод
Задача прогнозирования временных рядов имеет высокую актуальность для многих предметных областей и является неотъемлемой частью повседневной работы. К настоящему времени разработано множество моделей для решения задачи прогнозирования временного ряда, среди которых наибольшую применимость имеют нейросетевые модели.
Список использованной литературы:
5. П.И. Аверин, Н.И.Крайнюков. Вариант решения задачи прогнозирования признаков разрушения металлов с помощью нейронных сетей на основе данных вейвлет — анализа импульсов акустической эмиссии, 2011.
6. Галушкин А.И. Нейронные сети: основы теории. — М.: Горячая линия — Телеком, 2010. — 496 с.
7. С. Хайкин. Нейронные сети: полный курс. 2-е изд. М., «Вильямс», 2006.
8. Электронный ресурс: http://www.intuit.ru/
© Т.В. Любимова, А.В. Горелова, 2015
d =
УДК 621.452.322
О.Д. Лянцев
д.т.н., профессор кафедры АСУ Уфимский государственный авиационный технический университет
г. Уфа, Российская Федерация А.В. Казанцев аспирант 3 года обучения кафедры АСУ Уфимский государственный авиационный технический университет
г. Уфа, Российская Федерация А.С. Васин
аспирант 3 года обучения кафедры АСУ Уфимский государственный авиационный технический университет
г. Уфа, Российская Федерация
МЕТОДИКА ИДЕНТИФИКАЦИИ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ ГАЗОГЕНЕРАТОРА ТРДД
Аннотация
Предложена методика идентификации передаточных функций газогенератора ТРДД с использованием кубических сплайнов и метода МНК.
Ключевые слова
Идентификация, методика идентификации, передаточная функция, газогенератор, турбореактивный
двигатель, кубические сплайны, МНК.
В настоящее время весьма интенсивно развиваются методы идентификации динамических моделей газотурбинных двигателей, основанные на результатах летных испытаний силовых установок самолетов. Процедура идентификации необходима для уточнения структуры и параметров САУ ГТД, что, в свою очередь, позволяет повысить точность и качество управления силовыми установками самолетов, а также создать встроенные в состав САУ бортовые динамические модели, учитывающие индивидуальные характеристики двигателей. Таким образом, совершенствование методик идентификации математических моделей ГТД как объекта управления и автоматизация их основных этапов является актуальной задачей.
В статье рассматривается методика идентификации параметров линейной модели газогенератора двухвального ГТД на примере двигателя Д-136 и применение вычислительной среды МАТЬАБ для автоматизации всех этапов предложенной методики.
Исходными данными для процедуры расчета параметров линейной модели газогенератора служат переходные процессы по двигательным параметрам, полученные в результате натурных экспериментов на моторном стенде. На рис. 1 — 5 представлены исходные экспериментальные процессы по следующим параметрам: частоте вращения ротора низкого давления Пх, частоте вращения ротора высокого давления Я2, температуре газов за турбиной низкого
давления Т* , давлению воздуха за компрессором высокого давления Р2 и расходу топлива ^ . Частота регистрации экспериментальных данных составляет т=0,02 с.
^jfTW^rC-r- -,
/
/
/
i
Рисунок 1 — Исходный переходной процесс по расходу топлива От
Рисунок 2 — Исходный переходной процесс по частоте вращения П1
x 10
1420
1.205
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
1400
1.2
1380
1.195
1360
1340
== 1.19
1320
1.185
1300
1280
10
15
10
15
В первой части были рассмотрены: структура, топология, функции активации и обучающее множество. В этой части попробую объяснить как происходит обучение сверточной нейронной сети.
Обучение сверточной нейронной сети
На начальном этапе нейронная сеть является необученной (ненастроенной). В общем смысле под обучением понимают последовательное предъявление образа на вход нейросети, из обучающего набора, затем полученный ответ сравнивается с желаемым выходом, в нашем случае это 1 – образ представляет лицо, минус 1 – образ представляет фон (не лицо), полученная разница между ожидаемым ответом и полученным является результат функции ошибки (дельта ошибки). Затем эту дельту ошибки необходимо распространить на все связанные нейроны сети.
Таким образом обучение нейронной сети сводится к минимизации функции ошибки, путем корректировки весовых коэффициентов синаптических связей между нейронами. Под функцией ошибки понимается разность между полученным ответом и желаемым. Например, на вход был подан образ лица, предположим, что выход нейросети был 0.73, а желаемый результат 1 (т.к. образ лица), получим, что ошибка сети является разницей, то есть 0.27. Затем веса выходного слоя нейронов корректируются в соответствии с ошибкой. Для нейронов выходного слоя известны их фактические и желаемые значения выходов. Поэтому настройка весов связей для таких нейронов является относительно простой. Однако для нейронов предыдущих слоев настройка не столь очевидна. Долгое время не было известно алгоритма распространения ошибки по скрытым слоям.
Алгоритм обратного распространения ошибки
Для обучения описанной нейронной сети был использован алгоритм обратного распространения ошибки (backpropagation). Этот метод обучения многослойной нейронной сети называется обобщенным дельта-правилом. Метод был предложен в 1986 г. Румельхартом, Макклеландом и Вильямсом. Это ознаменовало возрождение интереса к нейронным сетям, который стал угасать в начале 70-х годов. Данный алгоритм является первым и основным практически применимым для обучения многослойных нейронных сетей.
Для выходного слоя корректировка весов интуитивна понятна, но для скрытых слоев долгое время не было известно алгоритма. Веса скрытого нейрона должны изменяться прямо пропорционально ошибке тех нейронов, с которыми данный нейрон связан. Вот почему обратное распространение этих ошибок через сеть позволяет корректно настраивать веса связей между всеми слоями. В этом случае величина функции ошибки уменьшается и сеть обучается.
Основные соотношения метода обратного распространения ошибки получены при следующих обозначениях:
Величина ошибки определяется по формуле 2.8 среднеквадратичная ошибка:
Неактивированное состояние каждого нейрона j для образа p записывается в виде взвешенной суммы по формуле 2.9:
Выход каждого нейрона j является значением активационной функции

В качестве метода минимизации ошибки используется метод градиентного спуска, суть этого метода сводится к поиску минимума (или максимума) функции за счет движения вдоль вектора градиента. Для поиска минимума движение должно быть осуществляться в направлении антиградиента. Метод градиентного спуска в соответствии с рисунком 2.7.
Градиент функции потери представляет из себя вектор частных производных, вычисляющийся по формуле 2.11:
Производную функции ошибки по конкретному образу можно записать по правилу цепочки, формула 2.12:
Ошибка нейрона 
Ошибка δ для скрытого слоя рассчитывается по формуле 2.13:
Алгоритм распространения ошибки сводится к следующим этапам:
- прямое распространение сигнала по сети, вычисления состояния нейронов;
- вычисление значения ошибки δ для выходного слоя;
- обратное распространение: последовательно от конца к началу для всех скрытых слоев вычисляем δ по формуле 2.13;
- обновление весов сети на вычисленную ранее δ ошибки.
Алгоритм обратного распространения ошибки в многослойном персептроне продемонстрирован ниже:
До этого момента были рассмотрены случаи распространения ошибки по слоям персептрона, то есть по выходному и скрытому, но помимо них, в сверточной нейросети имеются подвыборочный и сверточный.
Расчет ошибки на подвыборочном слое
Расчет ошибки на подвыборочном слое представляется в нескольких вариантах. Первый случай, когда подвыборочный слой находится перед полносвязным, тогда он имеет нейроны и связи такого же типа, как в полносвязном слое, соответственно вычисление δ ошибки ничем не отличается от вычисления δ скрытого слоя. Второй случай, когда подвыборочный слой находится перед сверточным, вычисление δ происходит путем обратной свертки. Для понимания обратно свертки, необходимо сперва понять обычную свертку и то, что скользящее окно по карте признаков (во время прямого распространения сигнала) можно интерпретировать, как обычный скрытый слой со связями между нейронами, но главное отличие — это то, что эти связи разделяемы, то есть одна связь с конкретным значением веса может быть у нескольких пар нейронов, а не только одной. Интерпретация операции свертки в привычном многослойном виде в соответствии с рисунком 2.8.
Рисунок 2.8 — Интерпретация операции свертки в многослойный вид, где связи с одинаковым цветом имеют один и тот же вес. Синим цветом обозначена подвыборочная карта, разноцветным – синаптическое ядро, оранжевым – получившаяся свертка
Теперь, когда операция свертки представлена в привычном многослойном виде, можно интуитивно понять, что вычисление дельт происходит таким же образом, как и в скрытом слое полносвязной сети. Соответственно имея вычисленные ранее дельты сверточного слоя можно вычислить дельты подвыборочного, в соответствии с рисунком 2.9.
Рисунок 2.9 — Вычисление δ подвыборочного слоя за счет δ сверточного слоя и ядра
Обратная свертка – это тот же самый способ вычисления дельт, только немного хитрым способом, заключающийся в повороте ядра на 180 градусов и скользящем процессе сканирования сверточной карты дельт с измененными краевыми эффектами. Простыми словами, нам необходимо взять ядро сверточной карты (следующего за подвыборочным слоем) повернуть его на 180 градусов и сделать обычную свертку по вычисленным ранее дельтам сверточной карты, но так чтобы окно сканирования выходило за пределы карты. Результат операции обратной свертки в соответствии с рисунком 2.10, цикл прохода обратной свертки в соответствии с рисунком 2.11.
Рисунок 2.10 — Результат операции обратной свертки
Рисунок 2.11 — Повернутое ядро на 180 градусов сканирует сверточную карту
Расчет ошибки на сверточном слое
Обычно впередиидущий слой после сверточного это подвыборочный, соответственно наша задача вычислить дельты текущего слоя (сверточного) за счет знаний о дельтах подвыборочного слоя. На самом деле дельта ошибка не вычисляется, а копируется. При прямом распространении сигнала нейроны подвыборочного слоя формировались за счет неперекрывающегося окна сканирования по сверточному слою, в процессе которого выбирались нейроны с максимальным значением, при обратном распространении, мы возвращаем дельту ошибки тому ранее выбранному максимальному нейрону, остальные же получают нулевую дельту ошибки.
Заключение
Представив операцию свертки в привычном многослойном виде (рисунок 2.8), можно интуитивно понять, что вычисление дельт происходит таким же образом, как и в скрытом слое полносвязной сети.
Источники
Алгоритм обратного распространения ошибки для сверточной нейронной сети
Обратное распространение ошибки в сверточных слоях
раз и два
Обратное распространение ошибки в персептроне
Еще можно почитать в РГБ диссертацию Макаренко: АЛГОРИТМЫ И ПРОГРАММНАЯ СИСТЕМА КЛАССИФИКАЦИИ
Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс — обучение нейронных сетей.
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
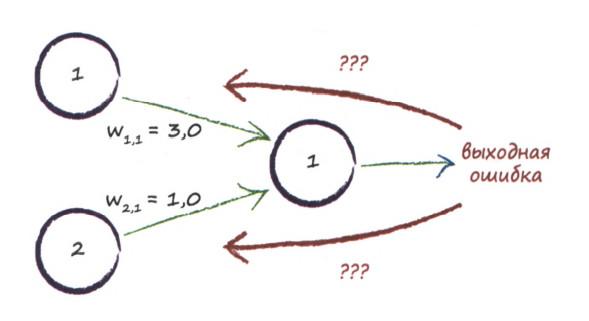
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):
То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| … | … | … |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| … | … | … |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно — рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части — обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 — для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий — обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети — это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:
Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос — устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель — необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
Здесь Delta w_{ij} — величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
Пусть функция ошибки от веса имеет следующий вид:
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:
В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:
Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:
Вывод прост — величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:
Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение Delta w (Delta w = w_2 — w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: Delta w = w_4 — w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | bold{Delta w} | Знак bold{Delta w} | Градиент |
|---|---|---|---|
| 1 rArr 2 | w_2 — w_1 | + | — |
| 3 rArr 4 | w_4 — w_3 | — | + |
Вывод напрашивается сам собой — величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
Delta w = -alpha cdot frac{dE}{dw}
Имеем в наличии:
- Delta w — величина, на которую необходимо изменить значение w.
- frac{dE}{dw} — градиент в этой точке.
- alpha — скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}}
Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:
Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:
Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:
Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t - 1}
То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат — Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1} — именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы — что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
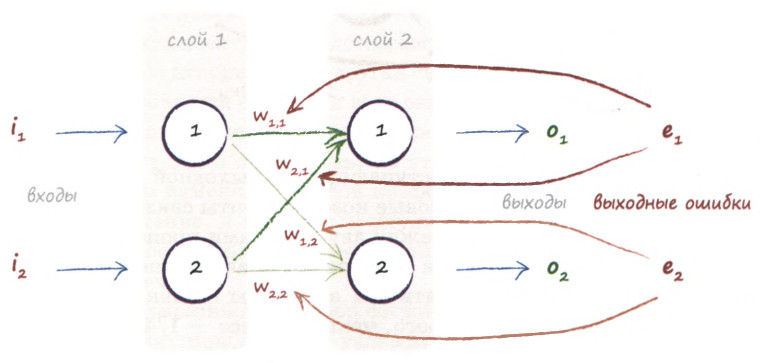
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:
Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано — задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}
Дополним пример числовыми значениями:
| Нейрон | bold{O_{net}} | bold{O_{correct}} | bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0
Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |
Тут в действие вступает уже проблема иного рода:
Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = (O_{correct, k} - O_{net, k})^2
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: frac{dE}{dw_{jk}} = frac{d}{d w_{jk}}(O_{correct, k} — O_{net, k})^2.
- Искомое по-прежнему: Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) cdot O_j
Здесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
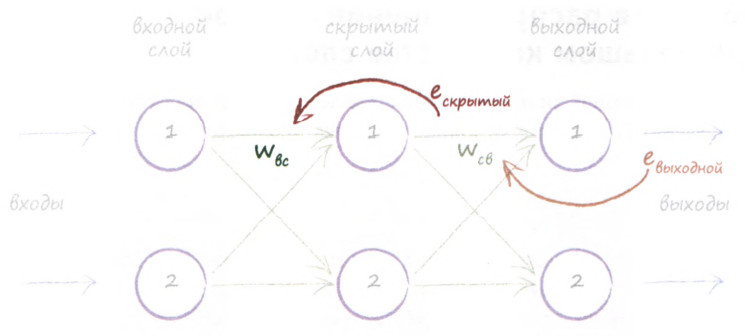
Освежим в памяти структуру сети:
Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) — ошибка нейрона k.
- O_j — тут все понятно, выходной сигнал нейрона j.
f{Large{prime}}(sum_{j}w_{jk}O_j) — значение производной функции активации. Причем, обратите внимание, что sum_{j}w_{jk}O_j — это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k).
Итог: frac{dE}{d w_{jk}} = -delta_k cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)medspace (1medspace-medspace f(x))
Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
frac{dE}{d w_{ij}} = -delta_j cdot O_i
Который примет следующий вид:
delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
frac{dE}{d w_{ij}} = -(sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j) cdot O_i
Снова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- скрытые слои: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Градиент: frac{dE}{d w_{ij}} = -delta_j cdot O_i
- Корректировка весовых коэффициентов: Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1}
Преобразуем последнюю формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход — входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход — обратное распространение ошибки — величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать — ссылка.
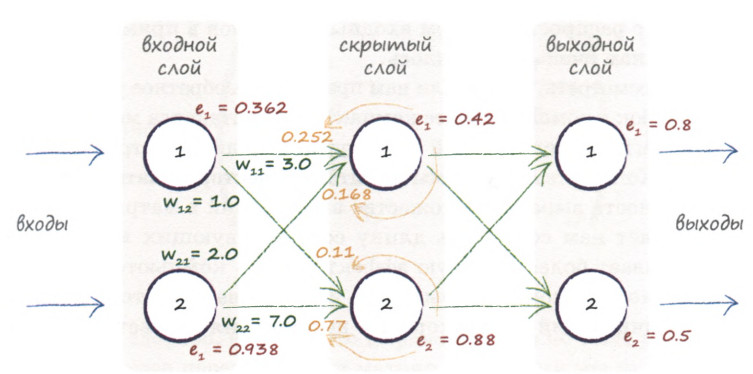
Вернемся к конкретному примеру для явной демонстрации этих принципов:
Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи — обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
- Рассчитываем величины ошибок для всех слоев:
- для выходного: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- для скрытых: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Далее используем полученные значения для расчета Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t — 1}
- И финишируем, рассчитывая новые значения весов: w_{ij medspace new} = w_{ij} + Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 — 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
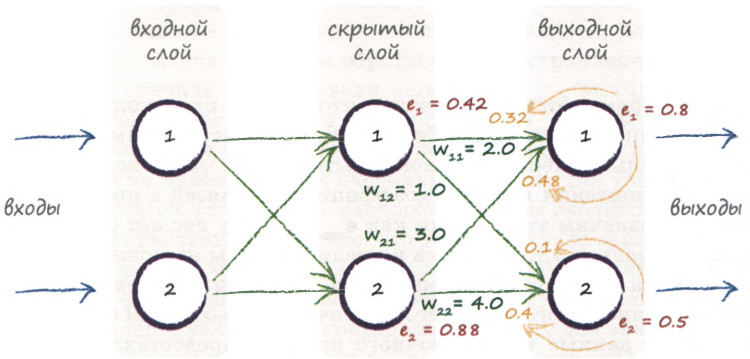
Возьмем нейронную сеть и зададим начальные значения весов:
Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = frac{1}{1 + e^{-x}}
И ее производная:
f{Large{prime}}(x) = f(x)medspace (1medspace-medspace f(x))
Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения alpha пусть будет равна 0.3, момент — gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 cdot w_{13} + O_2 cdot w_{23} = 0.6 cdot (-1medspace) + 0.7 cdot 1 = 0.1
I_4 = 0.6 cdot 2.5 + 0.7 cdot 0.4 = 1.78
I_5 = 0.6 cdot 1 + 0.7 cdot (-1.5medspace) = -0.45
На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3medspace) = 0.52 O_4 = 0.86 O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 cdot w_{36} + O_4 cdot w_{46} + O_5 cdot w_{56} = 0.52 cdot 2.2 + 0.86 cdot (-1.4medspace) + 0.39 cdot 0.56 = 0.158
I_7 = 0.52 cdot 0.34 + 0.86 cdot 1.05 + 0.39 cdot 3.1 = 2.288
O_6 = f(I_6) = 0.54
O_7 = 0.908
Добрались до выходного нейрона:
I_8 = O_6 cdot w_{68} + O_7 cdot w_{78} = 0.54 cdot 0.75 + 0.908 cdot (-0.22medspace) = 0.205
O_8 = O_{net} = f(I_8) = 0.551
Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
delta_8 = (O_{correct} - O_{net}) cdot f{Large{prime}}(I_8) = (O_{correct} - O_{net}) cdot f(I_8) cdot (1-f(I_8)) = (0.9 - 0.551medspace) cdot 0.551 cdot (1-0.551medspace) = 0.0863
delta_7 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_7) = (delta_8 cdot w_{78}) cdot f{Large{prime}}(I_7) = 0.0863 cdot (-0.22medspace) cdot 0.908 cdot (1 - 0.908medspace) = -0.0016
delta_6 = 0.086 cdot 0.75 cdot 0.54 cdot (1 - 0.54medspace) = 0.016
delta_5 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_5) = (delta_7 cdot w_{57} + delta_6 cdot w_{56}) cdot f{Large{prime}}(I_7) = (-0.0016 cdot 3.1 + 0.016 cdot 0.56) cdot 0.39 cdot (1 - 0.39medspace) = 0.001
delta_4 = (-0.0016 cdot 1.05 + 0.016 cdot (-1.4)) cdot 0.86 cdot (1 - 0.86medspace) = -0.003
delta_3 = (-0.0016 cdot 0.34 + 0.016 cdot 2.2) cdot 0.52 cdot (1 - 0.52medspace) = -0.0087
С расчетом ошибок закончили, следующий этап — расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Как вы помните, Delta w_{ij}^{t — 1} — это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
Delta w_{78} = alpha cdot delta_8 cdot O_7 = 0.3 cdot 0.0863 cdot 0.908 = 0.0235
Delta w_{68} = 0.3 cdot 0.0863 cdot 0.54= 0.014
Delta w_{57} = alpha cdot delta_7 cdot O_5 = 0.3 cdot (−0.0016medspace) cdot 0.39= -0.00019
Delta w_{47} = 0.3 cdot (−0.0016medspace) cdot 0.86= -0.0004
Delta w_{37} = 0.3 cdot (−0.0016medspace) cdot 0.52= -0.00025
Delta w_{56} = alpha cdot delta_6 cdot O_5 = 0.3 cdot 0.016 cdot 0.39= 0.0019
Delta w_{46} = 0.3 cdot 0.016 cdot 0.86= 0.0041
Delta w_{36} = 0.3 cdot 0.016 cdot 0.52= 0.0025
Delta w_{25} = alpha cdot delta_5 cdot O_2 = 0.3 cdot 0.001 cdot 0.7= 0.00021
Delta w_{15} = 0.3 cdot 0.001 cdot 0.6= 0.00018
Delta w_{24} = alpha cdot delta_4 cdot O_2 = 0.3 cdot (-0.003medspace) cdot 0.7= -0.00063
Delta w_{14} = 0.3 cdot (-0.003medspace) cdot 0.6= -0.00054
Delta w_{23} = alpha cdot delta_3 cdot O_2 = 0.3 cdot (−0.0087medspace) cdot 0.7= -0.00183
Delta w_{13} = 0.3 cdot (−0.0087medspace) cdot 0.6= -0.00157
И самый что ни на есть заключительный этап — непосредственно изменение значений весовых коэффициентов:
w_{78 medspace new} = w_{78} + Delta w_{78} = -0.22 + 0.0235 = -0.1965
w_{68 medspace new} = 0.75+ 0.014 = 0.764
w_{57 medspace new} = 3.1 + (−0.00019medspace) = 3.0998
w_{47 medspace new} = 1.05 + (−0.0004medspace) = 1.0496
w_{37 medspace new} = 0.34 + (−0.00025medspace) = 0.3398
w_{56 medspace new} = 0.56 + 0.0019 = 0.5619
w_{46 medspace new} = -1.4 + 0.0041 = -1.3959
w_{36 medspace new} = 2.2 + 0.0025 = 2.2025
w_{25 medspace new} = -1.5 + 0.00021 = -1.4998
w_{15 medspace new} = 1 + 0.00018 = 1.00018
w_{24 medspace new} = 0.4 + (−0.00063medspace) = 0.39937
w_{14 medspace new} = 2.5 + (−0.00054medspace) = 2.49946
w_{23 medspace new} = 1 + (−0.00183medspace) = 0.99817
w_{13 medspace new} = -1 + (−0.00157medspace) = -1.00157
И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!
Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.
Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.
Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_{m-1}(ldots (g_1(x)) ldots))$, то $frac{partial f}{partial x} = frac{partial g_m}{partial g_{m-1}}frac{partial g_{m-1}}{partial g_{m-2}}ldots frac{partial g_2}{partial g_1}frac{partial g_1}{partial x}$. Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с $frac{partial g_m}{partial g_{m-1}}$ и умножая каждый раз на частные производные предыдущего слоя.
Backpropagation в одномерном случае
В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид
$$f(w_0) = g_m(g_{m-1}(ldots g_1(w_0)ldots)),$$
где все $g_i$ скалярные. Тогда
$$f'(w_0) = g_m'(g_{m-1}(ldots g_1(w_0)ldots))cdot g’_{m-1}(g_{m-2}(ldots g_1(w_0)ldots))cdotldots cdot g’_1(w_0)$$
Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем
$$g_1(w_0), g_2(g_1(w_0)),ldots,g_{m-1}(ldots g_1(w_0)ldots),$$
то мы действуем следующим образом:
-
берём производную $g_m$ в точке $g_{m-1}(ldots g_1(w_0)ldots)$;
-
умножаем на производную $g_{m-1}$ в точке $g_{m-2}(ldots g_1(w_0)ldots)$;
-
и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):
Собирая все множители вместе, получаем:
$$frac{partial f}{partial w_0} = (-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_1} = x_1cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_2} = x_2cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.
Почему же нельзя просто пойти и начать везде вычислять производные?
В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^{r+1}$ — два последовательных промежуточных представления $Ntimes M$ и $Ntimes K$, связанных функцией $X^{r+1} = f^{r+1}(X^r)$. Предположим, что мы как-то посчитали производную $frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$ функции потерь $mathcal{L}$, тогда
$$frac{partialmathcal{L}}{partial X^{r}_{st}} = sum_{i,j}frac{partial f^{r+1}_{ij}}{partial X^{r}_{st}}frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$$
И мы видим, что, хотя оба градиента $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ и $frac{partialmathcal{L}}{partial X_{st}^{r}}$ являются просто матрицами, в ходе вычислений возникает «четырёхмерный кубик» $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, даже хранить который весьма болезненно: уж больно много памяти он требует ($N^2MK$ по сравнению с безобидными $NM + NK$, требуемыми для хранения градиентов). Поэтому хочется промежуточные производные $frac{partial f^{r+1}}{partial X^{r}}$ рассматривать не как вычисляемые объекты $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, а как преобразования, которые превращают $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ в $frac{partialmathcal{L}}{partial X_{st}^{r}}$. Целью следующих глав будет именно это: понять, как преобразуется градиент в ходе error backpropagation при переходе через тот или иной слой.
Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?
Встречный вопрос. Найдите производную функции по вектору $x$:
$$f(x) = x^TAx, Ain Mat_{n}{mathbb{R}}text{ — матрица размера }ntimes n$$
А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.
Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.
Градиент сложной функции
Напомним, что формула производной сложной функции выглядит следующим образом:
$$left[D_{x_0} (color{#5002A7}{u} circ color{#4CB9C0}{v}) right](h) = color{#5002A7}{left[D_{v(x_0)} u right]} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$
Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда
$$left[D_{x_0} f right] (x-x_0) = langlenabla_{x_0} f, x-x_0rangle.$$
С другой стороны,
$$left[D_{h(x_0)} g right] left(left[D_{x_0}h right] (x-x_0)right) = langlenabla_{h_{x_0}} g, left[D_{x_0} hright] (x-x_0)rangle = langleleft[D_{x_0} hright]^* nabla_{h(x_0)} g, x-x_0rangle.$$
То есть $color{#FFC100}{nabla_{x_0} f} = color{#348FEA}{left[D_{x_0} h right]}^* color{#FFC100}{nabla_{h(x_0)}}g$ — применение сопряжённого к $D_{x_0} h$ линейного отображения к вектору $nabla_{h(x_0)} g$.
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^{k-1}$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^{k-1}$:
Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.
Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.
Градиенты для типичных слоёв
Рассмотрим несколько важных примеров.
Примеры
-
$f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:
$$vbegin{pmatrix}
x_1
vdots
x_N
end{pmatrix}
= begin{pmatrix}
v(x_1)
vdots
v(x_N)
end{pmatrix}$$Тогда, как мы знаем,
$$left[D_{x_0} fright] (h) = langlenabla_{x_0} f, hrangle = left[nabla_{x_0} fright]^T h.$$
Следовательно,
$$begin{multline*}
left[D_{v(x_0)} uright] left( left[ D_{x_0} vright] (h)right) = left[nabla_{v(x_0)} uright]^T left(v'(x_0) odot hright) =[0.1cm]
= sumlimits_i left[nabla_{v(x_0)} uright]_i v'(x_{0i})h_i
= langleleft[nabla_{v(x_0)} uright] odot v'(x_0), hrangle.
end{multline*},$$где $odot$ означает поэлементное перемножение. Окончательно получаем
$$color{#348FEA}{nabla_{x_0} f = left[nabla_{v(x_0)}uright] odot v'(x_0) = v'(x_0) odot left[nabla_{v(x_0)} uright]}$$
Отметим, что если $x$ и $h(x)$ — это просто векторы, то мы могли бы вычислять всё и по формуле $frac{partial f}{partial x_i} = sum_jbig(frac{partial z_j}{partial x_i}big)cdotbig(frac{partial h}{partial z_j}big)$. В этом случае матрица $big(frac{partial z_j}{partial x_i}big)$ была бы диагональной (так как $z_j$ зависит только от $x_j$: ведь $h$ берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если $x$ и $h(x)$ — матрицы, то $big(frac{partial z_j}{partial x_i}big)$ представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.
-
$f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,
$$left[D_{X_0} f right] (X-X_0) = text{tr}, left(left[nabla_{X_0} fright]^T (X-X_0)right).$$
Тогда
$$begin{multline*}
left[ D_{X_0W} g right] left(left[D_{X_0} left( ast Wright)right] (H)right) =
left[ D_{X_0W} g right] left(HWright)=
= text{tr}, left( left[nabla_{X_0W} g right]^T cdot (H) W right) =
=
text{tr} , left(W left[nabla_{X_0W} (g) right]^T cdot (H)right) = text{tr} , left( left[left[nabla_{X_0W} gright] W^Tright]^T (H)right)
end{multline*}$$Здесь через $ast W$ мы обозначили отображение $Y hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:
$$
text{tr} , (A B C) = text{tr} , (C A B),
$$где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем
$$color{#348FEA}{nabla_{X_0} f = left[nabla_{X_0W} (g) right] cdot W^T}$$
-
$f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W — W_0$ имеем
$$
left[D_{W_0} f right] (H) = text{tr} , left( left[nabla_{W_0} f right]^T (H)right)
$$Тогда
$$ begin{multline*}
left[D_{XW_0} g right] left( left[D_{W_0} left(X astright) right] (H)right) = left[D_{XW_0} g right] left( XH right) =
= text{tr} , left( left[nabla_{XW_0} g right]^T cdot X (H)right) =
text{tr}, left(left[X^T left[nabla_{XW_0} g right] right]^T (H)right)
end{multline*} $$Здесь через $X ast$ обозначено отображение $Y hookrightarrow XY$. Значит,
$$color{#348FEA}{nabla_{X_0} f = X^T cdot left[nabla_{XW_0} (g)right]}$$
-
$f(X) = g(softmax(X))$, где $X$ — матрица $Ntimes K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$
$$softmax(x) = left(frac{e^{x_1}}{sum_te^{x_t}},ldots,frac{e^{x_K}}{sum_te^{x_t}}right)$$
В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $frac{partial s_l}{partial x_j}$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = frac{e^{x_l}} {sum_te^{x_t}}$. Нетрудно проверить, что
$$frac{partial s_l}{partial x_j} = begin{cases}
s_j(1 — s_j), & j = l,
-s_ls_j, & jne l
end{cases}$$Так как softmax вычисляется независимо от каждой строчки, то
$$frac{partial s_{rl}}{partial x_{ij}} = begin{cases}
s_{ij}(1 — s_{ij}), & r=i, j = l,
-s_{il}s_{ij}, & r = i, jne l,
0, & rne i
end{cases},$$где через $s_{rl}$ мы обозначили для краткости $softmax(X)_{rl}$.
Теперь пусть $nabla_{rl} = nabla g = frac{partialmathcal{L}}{partial s_{rl}}$ (пришедший со следующего слоя, уже известный градиент). Тогда
$$frac{partialmathcal{L}}{partial x_{ij}} = sum_{r,l}frac{partial s_{rl}}{partial x_{ij}} nabla_{rl}$$
Так как $frac{partial s_{rl}}{partial x_{ij}} = 0$ при $rne i$, мы можем убрать суммирование по $r$:
$$ldots = sum_{l}frac{partial s_{il}}{partial x_{ij}} nabla_{il} = -s_{i1}s_{ij}nabla_{i1} — ldots + s_{ij}(1 — s_{ij})nabla_{ij}-ldots — s_{iK}s_{ij}nabla_{iK} =$$
$$= -s_{ij}sum_t s_{it}nabla_{it} + s_{ij}nabla_{ij}$$
Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:
$$begin{multline*}
color{#348FEA}{nabla_{X_0}f =}
color{#348FEA}{= -softmax(X_0) odot text{sum}left(
softmax(X_0)odotnabla_{softmax(X_0)}g, text{ axis = 1}
right) +}
color{#348FEA}{softmax(X_0)odot nabla_{softmax(X_0)}g}
end{multline*}
$$
Backpropagation в общем виде
Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:
- Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, ldots, X^m = widehat{y}$.
- Вычислить все градиенты с помощью backward pass.
- С помощью полученных градиентов совершить шаг SGD.
Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.
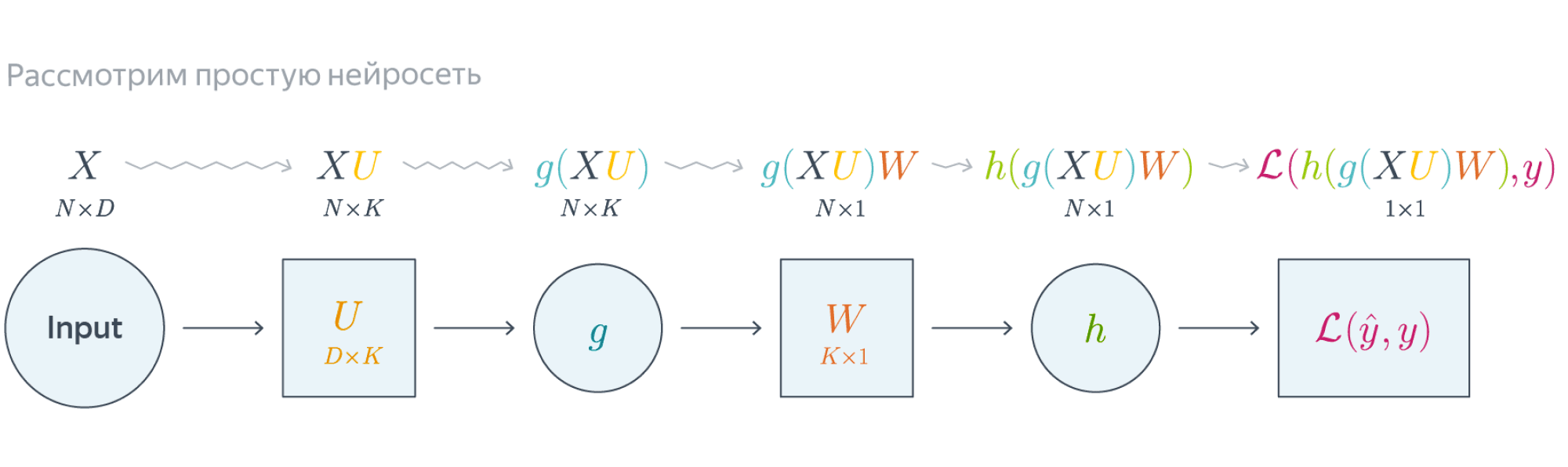
$$nabla_{W_0}mathcal{L} = nabla_{W_0}{left({vphantom{frac12}mathcal{L}circ hcircleft[Wmapsto g(XU_0)Wright]}right)}=$$
$$=g(XU_0)^Tnabla_{g(XU_0)W_0}(mathcal{L}circ h) = underbrace{g(XU_0)^T}_{ktimes N}cdot
left[vphantom{frac12}underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes 1}odot
underbrace{nabla_{hleft(vphantom{int_0^1}g(XU_0)W_0right)}mathcal{L}}_{Ntimes 1}right]$$
Итого матрица $ktimes 1$, как и $W_0$
$$nabla_{U_0}mathcal{L} = nabla_{U_0}left(vphantom{frac12}
mathcal{L}circ hcircleft[Ymapsto YW_0right]circ gcircleft[ Umapsto XUright]
right)=$$
$$=X^Tcdotnabla_{XU^0}left(vphantom{frac12}mathcal{L}circ hcirc [Ymapsto YW_0]circ gright) =$$
$$=X^Tcdotleft(vphantom{frac12}g'(XU_0)odot
nabla_{g(XU_0)}left[vphantom{in_0^1}mathcal{L}circ hcirc[Ymapsto YW_0right]
right)$$
$$=ldots = underset{Dtimes N}{X^T}cdotleft(vphantom{frac12}
underbrace{g'(XU_0)}_{Ntimes K}odot
underbrace{left[vphantom{int_0^1}left(
underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes1}odotunderbrace{nabla_{h(vphantom{int_0^1}gleft(XU_0right)W_0)}mathcal{L}}_{Ntimes 1}
right)cdot underbrace{W^T}_{1times K}right]}_{Ntimes K}
right)$$
Итого $Dtimes K$, как и $U_0$
Схематически это можно представить следующим образом:
Backpropagation для двуслойной нейронной сети
Если вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = sigma$)Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:
$$
widehat{y} = sigma(X^1 W^2) = sigmaBig(big(sigma(X^0 W^1 )big) W^2 Big).
$$
Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.
Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = sigma(X^0 W^1_0)$, $X^3 = sigma(X^0 W^1_0) W^2_0$, $X^4 = sigma(sigma(X^0 W^1_0) W^2_0) = widehat{y}$. Они понадобятся нам дальше.
Для полученных предсказаний вычисляется значение функции потерь:
$$
l = mathcal{L}(y, widehat{y}) = y log(widehat{y}) + (1-y) log(1-widehat{y}).
$$
Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.
-
Градиент $mathcal{L}$ по предсказаниям имеет вид
$$
nabla_{widehat{y}}l = frac{y}{widehat{y}} — frac{1 — y}{1 — widehat{y}} = frac{y — widehat{y}}{widehat{y} (1 — widehat{y})},
$$где, напомним, $ widehat{y} = sigma(X^3) = sigmaBig(big(sigma(X^0 W^1_0 )big) W^2_0 Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).
-
Следующий слой — поэлементное взятие $sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $sigma$, в которую подставлено предыдущее промежуточное представление:
$$
nabla_{X^3}l = sigma'(X^3)odotnabla_{widehat{y}}l = sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — widehat{y}}{widehat{y} (1 — widehat{y})} =
$$$$
= sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — sigma(X^3)}{sigma(X^3) (1 — sigma(X^3))} =
y — sigma(X^3)
$$ -
Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:
$$
color{blue}{nabla_{W^2_0}l} = (X^2)^Tcdot nabla_{X^3}l = (X^2)^Tcdot(y — sigma(X^3)) =
$$$$
= color{blue}{left( sigma(X^0W^1_0) right)^T cdot (y — sigma(sigma(X^0W^1_0)W^2_0))}
$$Аналогичным образом
$$
nabla_{X^2}l = nabla_{X^3}lcdot (W^2_0)^T = (y — sigma(X^3))cdot (W^2_0)^T =
$$$$
= (y — sigma(X^2W_0^2))cdot (W^2_0)^T
$$ -
Следующий слой — снова взятие $sigma$.
$$
nabla_{X^1}l = sigma'(X^1)odotnabla_{X^2}l = sigma(X^1)left( 1 — sigma(X^1) right) odot left( (y — sigma(X^2W_0^2))cdot (W^2_0)^T right) =
$$$$
= sigma(X^1)left( 1 — sigma(X^1) right) odotleft( (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^T right)
$$ -
Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:
$$
color{blue}{nabla_{W^1_0}l} = (X^0)^Tcdot nabla_{X^1}l = (X^0)^Tcdot big( sigma(X^1) left( 1 — sigma(X^1) right) odot (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^Tbig) =
$$$$
= color{blue}{(X^0)^Tcdotbig(sigma(X^0W^1_0)left( 1 — sigma(X^0W^1_0) right) odot (y — sigma(sigma(X^0W^1_0)W_0^2))cdot (W^2_0)^Tbig) }
$$
Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.
Автоматизация и autograd
Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^{k-1}mapsto X^k$ с параметрами $W^k$ уметь:
- превращать $nabla_{X^k_0}mathcal{L}$ в $nabla_{X^{k-1}_0}mathcal{L}$ (градиент по выходу в градиент по входу);
- считать градиент по его параметрам $nabla_{W^k_0}mathcal{L}$.
При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.
Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).
Но это лишь начало
Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.
Нейронные сети для начинающих. Часть 2 +38
Алгоритмы, Машинное обучение
Рекомендация: подборка платных и бесплатных курсов таргетированной рекламе — https://katalog-kursov.ru/
Добро пожаловать во вторую часть руководства по нейронным сетям. Сразу хочу принести извинения всем кто ждал вторую часть намного раньше. По определенным причинам мне пришлось отложить ее написание. На самом деле я не ожидал, что у первой статьи будет такой спрос и что так много людей заинтересует данная тема. Взяв во внимание ваши комментарии, я постараюсь предоставить вам как можно больше информации и в то же время сохранить максимально понятный способ ее изложения. В данной статье, я буду рассказывать о способах обучения/тренировки нейросетей (в частности метод обратного распространения) и если вы, по каким-либо причинам, еще не прочитали первую часть, настоятельно рекомендую начать с нее. В процессе написания этой статьи, я хотел также рассказать о других видах нейросетей и методах тренировки, однако, начав писать про них, я понял что это пойдет вразрез с моим методом изложения. Я понимаю, что вам не терпится получить как можно больше информации, однако эти темы очень обширны и требуют детального анализа, а моей основной задачей является не написать очередную статью с поверхностным объяснением, а донести до вас каждый аспект затронутой темы и сделать статью максимально легкой в освоении. Спешу расстроить любителей “покодить”, так как я все еще не буду прибегать к использованию языка программирования и буду объяснять все “на пальцах”. Достаточно вступления, давайте теперь продолжим изучение нейросетей.
Что такое нейрон смещения?
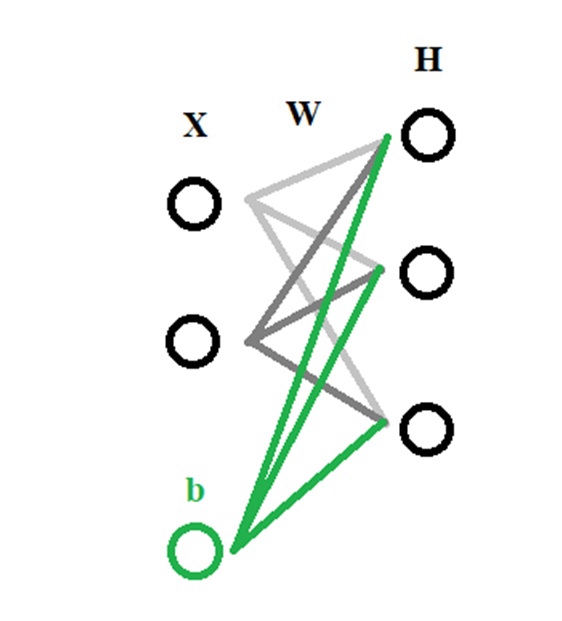
Перед тем как начать нашу основную тему, мы должны ввести понятие еще одного вида нейронов — нейрон смещения. Нейрон смещения или bias нейрон — это третий вид нейронов, используемый в большинстве нейросетей. Особенность этого типа нейронов заключается в том, что его вход и выход всегда равняются 1 и они никогда не имеют входных синапсов. Нейроны смещения могут, либо присутствовать в нейронной сети по одному на слое, либо полностью отсутствовать, 50/50 быть не может (красным на схеме обозначены веса и нейроны которые размещать нельзя). Соединения у нейронов смещения такие же, как у обычных нейронов — со всеми нейронами следующего уровня, за исключением того, что синапсов между двумя bias нейронами быть не может. Следовательно, их можно размещать на входном слое и всех скрытых слоях, но никак не на выходном слое, так как им попросту не с чем будет формировать связь.
Для чего нужен нейрон смещения?
Нейрон смещения нужен для того, чтобы иметь возможность получать выходной результат, путем сдвига графика функции активации вправо или влево. Если это звучит запутанно, давайте рассмотрим простой пример, где есть один входной нейрон и один выходной нейрон. Тогда можно установить, что выход O2 будет равен входу H1, умноженному на его вес, и пропущенному через функцию активации (формула на фото слева). В нашем конкретном случае, будем использовать сигмоид.
Из школьного курса математики, мы знаем, что если взять функцию y = ax+b и менять у нее значения “а”, то будет изменяться наклон функции (цвета линий на графике слева), а если менять “b”, то мы будем смещать функцию вправо или влево (цвета линий на графике справа). Так вот “а” — это вес H1, а “b” — это вес нейрона смещения B1. Это грубый пример, но примерно так все и работает (если вы посмотрите на функцию активации справа на изображении, то заметите очень сильное сходство между формулами). То есть, когда в ходе обучения, мы регулируем веса скрытых и выходных нейронов, мы меняем наклон функции активации. Однако, регулирование веса нейронов смещения может дать нам возможность сдвинуть функцию активации по оси X и захватить новые участки. Иными словами, если точка, отвечающая за ваше решение, будет находиться, как показано на графике слева, то ваша НС никогда не сможет решить задачу без использования нейронов смещения. Поэтому, вы редко встретите нейронные сети без нейронов смещения.
Также нейроны смещения помогают в том случае, когда все входные нейроны получают на вход 0 и независимо от того какие у них веса, они все передадут на следующий слой 0, но не в случае присутствия нейрона смещения. Наличие или отсутствие нейронов смещения — это гиперпараметр (об этом чуть позже). Одним словом, вы сами должны решить, нужно ли вам использовать нейроны смещения или нет, прогнав НС с нейронами смешения и без них и сравнив результаты.
ВАЖНО знать, что иногда на схемах не обозначают нейроны смещения, а просто учитывают их веса при вычислении входного значения например:
input = H1*w1+H2*w2+b3
b3 = bias*w3
Так как его выход всегда равен 1, то можно просто представить что у нас есть дополнительный синапс с весом и прибавить к сумме этот вес без упоминания самого нейрона.
Как сделать чтобы НС давала правильные ответы?
Ответ прост — нужно ее обучать. Однако, насколько бы прост не был ответ, его реализация в плане простоты, оставляет желать лучшего. Существует несколько методов обучения НС и я выделю 3, на мой взгляд, самых интересных:
- Метод обратного распространения (Backpropagation)
- Метод упругого распространения (Resilient propagation или Rprop)
- Генетический Алгоритм (Genetic Algorithm)
Об Rprop и ГА речь пойдет в других статьях, а сейчас мы с вами посмотрим на основу основ — метод обратного распространения, который использует алгоритм градиентного спуска.
Что такое градиентный спуск?
Это способ нахождения локального минимума или максимума функции с помощью движения вдоль градиента. Если вы поймете суть градиентного спуска, то у вас не должно возникнуть никаких вопросов во время использования метода обратного распространения. Для начала, давайте разберемся, что такое градиент и где он присутствует в нашей НС. Давайте построим график, где по оси х будут значения веса нейрона(w) а по оси у — ошибка соответствующая этому весу(e).
Посмотрев на этот график, мы поймем, что график функция f(w) является зависимостью ошибки от выбранного веса. На этом графике нас интересует глобальный минимум — точка (w2,e2) или, иными словами, то место где график подходит ближе всего к оси х. Эта точка будет означать, что выбрав вес w2 мы получим самую маленькую ошибку — e2 и как следствие, самый лучший результат из всех возможных. Найти же эту точку нам поможет метод градиентного спуска (желтым на графике обозначен градиент). Соответственно у каждого веса в нейросети будет свой график и градиент и у каждого надо найти глобальный минимум.
Так что же такое, этот градиент? Градиент — это вектор который определяет крутизну склона и указывает его направление относительно какой либо из точек на поверхности или графике. Чтобы найти градиент нужно взять производную от графика по данной точке (как это и показано на графике). Двигаясь по направлению этого градиента мы будем плавно скатываться в низину. Теперь представим что ошибка — это лыжник, а график функции — гора. Соответственно, если ошибка равна 100%, то лыжник находиться на самой вершине горы и если ошибка 0% то в низине. Как все лыжники, ошибка стремится как можно быстрее спуститься вниз и уменьшить свое значение. В конечном случае у нас должен получиться следующий результат:
Представьте что лыжника забрасывают, с помощью вертолета, на гору. На сколько высоко или низко зависит от случая (аналогично тому, как в нейронной сети при инициализации веса расставляются в случайном порядке). Допустим ошибка равна 90% и это наша точка отсчета. Теперь лыжнику нужно спуститься вниз, с помощью градиента. На пути вниз, в каждой точке мы будем вычислять градиент, что будет показывать нам направление спуска и при изменении наклона, корректировать его. Если склон будет прямым, то после n-ого количества таких действий мы доберемся до низины. Но в большинстве случаев склон (график функции) будет волнистый и наш лыжник столкнется с очень серьезной проблемой — локальный минимум. Я думаю все знают, что такое локальный и глобальный минимум функции, для освежения памяти вот пример. Попадание в локальный минимум чревато тем, что наш лыжник навсегда останется в этой низине и никогда не скатиться с горы, следовательно мы никогда не сможем получить правильный ответ. Но мы можем избежать этого, снарядив нашего лыжника реактивным ранцем под названием момент (momentum). Вот краткая иллюстрация момента:
Как вы уже наверное догадались, этот ранец придаст лыжнику необходимое ускорение чтобы преодолеть холм, удерживающий нас в локальном минимуме, однако здесь есть одно НО. Представим что мы установили определенное значение параметру момент и без труда смогли преодолеть все локальные минимумы, и добраться до глобального минимума. Так как мы не можем просто отключить реактивный ранец, то мы можем проскочить глобальный минимум, если рядом с ним есть еще низины. В конечном случае это не так важно, так как рано или поздно мы все равно вернемся обратно в глобальный минимум, но стоит помнить, что чем больше момент, тем больше будет размах с которым лыжник будет кататься по низинам. Вместе с моментом в методе обратного распространения также используется такой параметр как скорость обучения (learning rate). Как наверняка многие подумают, чем больше скорость обучения, тем быстрее мы обучим нейросеть. Нет. Скорость обучения, также как и момент, является гиперпараметром — величина которая подбирается путем проб и ошибок. Скорость обучения можно напрямую связать со скоростью лыжника и можно с уверенностью сказать — тише едешь дальше будешь. Однако здесь тоже есть определенные аспекты, так как если мы совсем не дадим лыжнику скорости то он вообще никуда не поедет, а если дадим маленькую скорость то время пути может растянуться на очень и очень большой период времени. Что же тогда произойдет если мы дадим слишком большую скорость?
Как видите, ничего хорошего. Лыжник начнет скатываться по неправильному пути и возможно даже в другом направлении, что как вы понимаете только отдалит нас от нахождения правильного ответа. Поэтому во всех этих параметрах нужно находить золотую середину чтобы избежать не сходимости НС (об этом чуть позже).
Что такое Метод Обратного Распространения (МОР)?
Вот мы и дошли до того момента, когда мы можем обсудить, как же все таки сделать так, чтобы ваша НС могла правильно обучаться и давать верные решения. Очень хорошо МОР визуализирован на этой гифке:
А теперь давайте подробно разберем каждый этап. Если вы помните то в предыдущей статье мы считали выход НС. По другому это называется передача вперед (Forward pass), то есть мы последовательно передаем информацию от входных нейронов к выходным. После чего мы вычисляем ошибку и основываясь на ней делаем обратную передачу, которая заключается в том, чтобы последовательно менять веса нейронной сети, начиная с весов выходного нейрона. Значение весов будут меняться в ту сторону, которая даст нам наилучший результат. В моих вычисления я буду пользоваться методом нахождения дельты, так как это наиболее простой и понятный способ. Также я буду использовать стохастический метод обновления весов (об этом чуть позже).
Теперь давайте продолжим с того места, где мы закончили вычисления в предыдущей статье.
Данные задачи из предыдущей статьи
Данные: I1=1, I2=0, w1=0.45, w2=0.78 ,w3=-0.12 ,w4=0.13 ,w5=1.5 ,w6=-2.3.
H1input = 1*0.45+0*-0.12=0.45
H1output = sigmoid(0.45)=0.61
H2input = 1*0.78+0*0.13=0.78
H2output = sigmoid(0.78)=0.69
O1input = 0.61*1.5+0.69*-2.3=-0.672
O1output = sigmoid(-0.672)=0.33
O1ideal = 1 (0xor1=1)
Error = ((1-0.33)^2)/1=0.45
Результат — 0.33, ошибка — 45%.
Так как мы уже подсчитали результат НС и ее ошибку, то мы можем сразу приступить к МОРу. Как я уже упоминал ранее, алгоритм всегда начинается с выходного нейрона. В таком случае давайте посчитаем для него значение ? (дельта) по формуле 1.
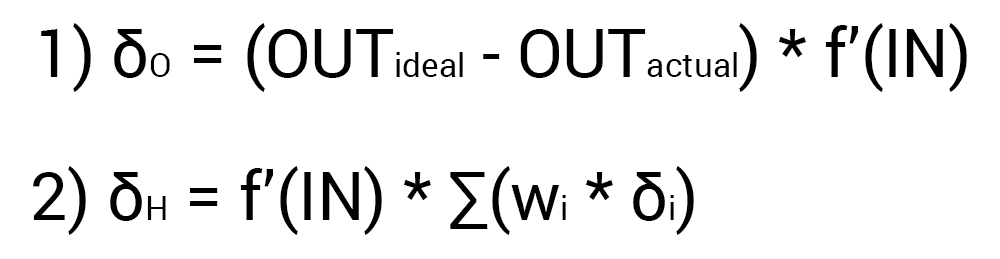
Таким образом наши вычисления для точки O1 будут выглядеть следующим образом.
Решение
O1output = 0.33
O1ideal = 1
Error = 0.45
?O1 = (1 — 0.33) * ( (1 — 0.33) * 0.33 ) = 0.148
На этом вычисления для нейрона O1 закончены. Запомните, что после подсчета дельты нейрона мы обязаны сразу обновить веса всех исходящих синапсов этого нейрона. Так как в случае с O1 их нет, мы переходим к нейронам скрытого уровня и делаем тоже самое за исключение того, что формула подсчета дельты у нас теперь вторая и ее суть заключается в том, чтобы умножить производную функции активации от входного значения на сумму произведений всех исходящих весов и дельты нейрона с которой этот синапс связан. Но почему формулы разные? Дело в том что вся суть МОР заключается в том чтобы распространить ошибку выходных нейронов на все веса НС. Ошибку можно вычислить только на выходном уровне, как мы это уже сделали, также мы вычислили дельту в которой уже есть эта ошибка. Следственно теперь мы будем вместо ошибки использовать дельту которая будет передаваться от нейрона к нейрону. В таком случае давайте найдем дельту для H1:
Решение
H1output = 0.61
w5 = 1.5
?O1 = 0.148
?H1 = ( (1 — 0.61) * 0.61 ) * ( 1.5 * 0.148 ) = 0.053
Теперь нам нужно найти градиент для каждого исходящего синапса. Здесь обычно вставляют 3 этажную дробь с кучей производных и прочим математическим адом, но в этом и вся прелесть использования метода подсчета дельт, потому что в конечном счете ваша формула нахождения градиента будет выглядеть вот так:
Здесь точка A это точка в начале синапса, а точка B на конце синапса. Таким образом мы можем подсчитать градиент w5 следующим образом:
Решение
H1output = 0.61
?O1 = 0.148
GRADw5 = 0.61 * 0.148 = 0.09
Сейчас у нас есть все необходимые данные чтобы обновить вес w5 и мы сделаем это благодаря функции МОР которая рассчитывает величину на которую нужно изменить тот или иной вес и выглядит она следующим образом:
Настоятельно рекомендую вам не игнорировать вторую часть выражения и использовать момент так как это вам позволит избежать проблем с локальным минимумом.
Здесь мы видим 2 константы о которых мы уже говорили, когда рассматривали алгоритм градиентного спуска: E (эпсилон) — скорость обучения, ? (альфа) — момент. Переводя формулу в слова получим: изменение веса синапса равно коэффициенту скорости обучения, умноженному на градиент этого веса, прибавить момент умноженный на предыдущее изменение этого веса (на 1-ой итерации равно 0). В таком случае давайте посчитаем изменение веса w5 и обновим его значение прибавив к нему ?w5.
Решение
E = 0.7
? = 0.3
w5 = 1.5
GRADw5 = 0.09
?w5(i-1) = 0
?w5 = 0.7 * 0.09 + 0 * 0.3 = 0.063
w5 = w5 + ?w5 = 1.563
Таким образом после применения алгоритма наш вес увеличился на 0.063. Теперь предлагаю сделать вам тоже самое для H2.
Решение
H2output = 0.69
w6 = -2.3
?O1 = 0.148
E = 0.7
? = 0.3
?w6(i-1) = 0
?H2 = ( (1 — 0.69) * 0.69 ) * ( -2.3 * 0.148 ) = -0.07
GRADw6 = 0.69 * 0.148 = 0.1
?w6 = 0.7 * 0.1 + 0 * 0.3 = 0.07
w6 = w6 + ?w6 = -2.2
И конечно не забываем про I1 и I2, ведь у них тоже есть синапсы веса которых нам тоже нужно обновить. Однако помним, что нам не нужно находить дельты для входных нейронов так как у них нет входных синапсов.
Решение
w1 = 0.45, ?w1(i-1) = 0
w2 = 0.78, ?w2(i-1) = 0
w3 = -0.12, ?w3(i-1) = 0
w4 = 0.13, ?w4(i-1) = 0
?H1 = 0.053
?H2 = -0.07
E = 0.7
? = 0.3
GRADw1 = 1 * 0.053 = 0.053
GRADw2 = 1 * -0.07 = -0.07
GRADw3 = 0 * 0.053 = 0
GRADw4 = 0 * -0.07 = 0
?w1 = 0.7 * 0.053 + 0 * 0.3 = 0.04
?w2 = 0.7 * -0.07 + 0 * 0.3 = -0.05
?w3 = 0.7 * 0 + 0 * 0.3 = 0
?w4 = 0.7 * 0 + 0 * 0.3 = 0
w1 = w1 + ?w1 = 0.5
w2 = w2 + ?w2 = 0.73
w3 = w3 + ?w3 = -0.12
w4 = w4 + ?w4 = 0.13
Теперь давайте убедимся в том, что мы все сделали правильно и снова посчитаем выход НС только уже с обновленными весами.
Решение
I1 = 1
I2 = 0
w1 = 0.5
w2 = 0.73
w3 = -0.12
w4 = 0.13
w5 = 1.563
w6 = -2.2
H1input = 1 * 0.5 + 0 * -0.12 = 0.5
H1output = sigmoid(0.5) = 0.62
H2input = 1 * 0.73 + 0 * 0.124 = 0.73
H2output = sigmoid(0.73) = 0.675
O1input = 0.62* 1.563 + 0.675 * -2.2 = -0.51
O1output = sigmoid(-0.51) = 0.37
O1ideal = 1 (0xor1=1)
Error = ((1-0.37)^2)/1=0.39
Результат — 0.37, ошибка — 39%.
Как мы видим после одной итерации МОР, нам удалось уменьшить ошибку на 0.04 (6%). Теперь нужно повторять это снова и снова, пока ваша ошибка не станет достаточно мала.
Что еще нужно знать о процессе обучения?
Нейросеть можно обучать с учителем и без (supervised, unsupervised learning).
Обучение с учителем — это тип тренировок присущий таким проблемам как регрессия и классификация (им мы и воспользовались в примере приведенном выше). Иными словами здесь вы выступаете в роли учителя а НС в роли ученика. Вы предоставляете входные данные и желаемый результат, то есть ученик посмотрев на входные данные поймет, что нужно стремиться к тому результату который вы ему предоставили.
Обучение без учителя — этот тип обучения встречается не так часто. Здесь нет учителя, поэтому сеть не получает желаемый результат или же их количество очень мало. В основном такой вид тренировок присущ НС у которых задача состоит в группировке данных по определенным параметрам. Допустим вы подаете на вход 10000 статей на хабре и после анализа всех этих статей НС сможет распределить их по категориям основываясь, например, на часто встречающихся словах. Статьи в которых упоминаются языки программирования, к программированию, а где такие слова как Photoshop, к дизайну.
Существует еще такой интересный метод, как обучение с подкреплением (reinforcement learning). Этот метод заслуживает отдельной статьи, но я попытаюсь вкратце описать его суть. Такой способ применим тогда, когда мы можем основываясь на результатах полученных от НС, дать ей оценку. Например мы хотим научить НС играть в PAC-MAN, тогда каждый раз когда НС будет набирать много очков мы будем ее поощрять. Иными словами мы предоставляем НС право найти любой способ достижения цели, до тех пор пока он будет давать хороший результат. Таким способом, сеть начнет понимать чего от нее хотят добиться и пытается найти наилучший способ достижения этой цели без постоянного предоставления данных “учителем”.
Также обучение можно производить тремя методами: стохастический метод (stochastic), пакетный метод (batch) и мини-пакетный метод (mini-batch). Существует очень много статей и исследований на тему того, какой из методов лучше и никто не может прийти к общему ответу. Я же сторонник стохастического метода, однако я не отрицаю тот факт, что каждый метод имеет свои плюсы и минусы.
Вкратце о каждом методе:
Стохастический (его еще иногда называют онлайн) метод работает по следующему принципу — нашел ?w, сразу обнови соответствующий вес.
Пакетный метод же работает по другому. Мы суммируем ?w всех весов на текущей итерации и только потом обновляем все веса используя эту сумму. Один из самых важных плюсов такого подхода — это значительная экономия времени на вычисление, точность же в таком случае может сильно пострадать.
Мини-пакетный метод является золотой серединой и пытается совместить в себе плюсы обоих методов. Здесь принцип таков: мы в свободном порядке распределяем веса по группам и меняем их веса на сумму ?w всех весов в той или иной группе.
Что такое гиперпараметры?
Гиперпараметры — это значения, которые нужно подбирать вручную и зачастую методом проб и ошибок. Среди таких значений можно выделить:
- Момент и скорость обучения
- Количество скрытых слоев
- Количество нейронов в каждом слое
- Наличие или отсутствие нейронов смещения
В других типах НС присутствуют дополнительные гиперпараметры, но о них мы говорить не будем. Подбор верных гиперпараметров очень важен и будет напрямую влиять на сходимость вашей НС. Понять стоит ли использовать нейроны смещения или нет достаточно просто. Количество скрытых слоев и нейронов в них можно вычислить перебором основываясь на одном простом правиле — чем больше нейронов, тем точнее результат и тем экспоненциально больше время, которое вы потратите на ее обучение. Однако стоит помнить, что не стоит делать НС с 1000 нейронов для решения простых задач. А вот с выбором момента и скорости обучения все чуточку сложнее. Эти гиперпараметры будут варьироваться, в зависимости от поставленной задачи и архитектуры НС. Например, для решения XOR скорость обучения может быть в пределах 0.3 — 0.7, но в НС которая анализирует и предсказывает цену акций, скорость обучения выше 0.00001 приводит к плохой сходимости НС. Не стоит сейчас заострять свое внимание на гиперпараметрах и пытаться досконально понять, как же их выбирать. Это придет с опытом, а пока что советую просто экспериментировать и искать примеры решения той или иной задачи в сети.
Что такое сходимость?
Сходимость говорит о том, правильная ли архитектура НС и правильно ли были подобраны гиперпараметры в соответствии с поставленной задачей. Допустим наша программа выводит ошибку НС на каждой итерации в лог. Если с каждой итерацией ошибка будет уменьшаться, то мы на верном пути и наша НС сходится. Если же ошибка будет прыгать вверх — вниз или застынет на определенном уровне, то НС не сходится. В 99% случаев это решается изменением гиперпараметров. Оставшийся 1% будет означать, что у вас ошибка в архитектуре НС. Также бывает, что на сходимость влияет переобучение НС.
Что такое переобучение?
Переобучение, как следует из названия, это состояние нейросети, когда она перенасыщена данными. Это проблема возникает, если слишком долго обучать сеть на одних и тех же данных. Иными словами, сеть начнет не учиться на данных, а запоминать и “зубрить” их. Соответственно, когда вы уже будете подавать на вход этой НС новые данные, то в полученных данных может появиться шум, который будет влиять на точность результата. Например, если мы будем показывать НС разные фотографии яблок (только красные) и говорить что это яблоко. Тогда, когда НС увидит желтое или зеленое яблоко, оно не сможет определить, что это яблоко, так как она запомнила, что все яблоки должны быть красными. И наоборот, когда НС увидит что-то красное и по форме совпадающее с яблоком, например персик, она скажет, что это яблоко. Это и есть шум. На графике шум будет выглядеть следующим образом.
Видно, что график функции сильно колеблется от точки к точке, которые являются выходными данными (результатом) нашей НС. В идеале, этот график должен быть менее волнистый и прямой. Чтобы избежать переобучения, не стоит долго тренировать НС на одних и тех же или очень похожих данных. Также, переобучение может быть вызвано большим количеством параметров, которые вы подаете на вход НС или слишком сложной архитектурой. Таким образом, когда вы замечаете ошибки (шум) в выходных данных после этапа обучения, то вам стоит использовать один из методов регуляризации, но в большинстве случаев это не понадобиться.
Заключение
Надеюсь эта статья смогла прояснить ключевые моменты такого нелегко предмета, как Нейронные сети. Однако я считаю, что сколько бы ты статей не прочел, без практики такую сложную тему освоить невозможно. Поэтому, если вы только в начале пути и хотите изучить эту перспективную и развивающуюся отрасль, то советую начать практиковаться с написания своей НС, а уже после прибегать к помощи различных фреймворков и библиотек. Также, если вам интересен мой метод изложения информации и вы хотите, чтобы я написал статьи на другие темы связанные с Машинным обучением, то проголосуйте в опросе ниже за ту тему которую вам интересна. До встречи в будущих статьях
Метод обратного распространения ошибок (англ. backpropagation) — метод вычисления градиента, который используется при обновлении весов в нейронной сети.
Содержание
- 1 Обучение как задача оптимизации
- 2 Дифференцирование для однослойной сети
- 2.1 Находим производную ошибки
- 3 Алгоритм
- 4 Недостатки алгоритма
- 4.1 Паралич сети
- 4.2 Локальные минимумы
- 5 Примечания
- 6 См. также
- 7 Источники информации
Обучение как задача оптимизации
Рассмотрим простую нейронную сеть без скрытых слоев, с двумя входными вершинами и одной выходной, в которых каждый нейрон использует линейную функцию активации, (обычно, многослойные нейронные сети используют нелинейные функции активации, линейные функции используются для упрощения понимания) которая является взвешенной суммой входных данных.
Простая нейронная сеть с двумя входными вершинами и одной выходной
Изначально веса задаются случайно. Затем, нейрон обучается с помощью тренировочного множества, которое в этом случае состоит из множества троек где и — это входные данные сети и — правильный ответ. Начальная сеть, приняв на вход и , вычислит ответ , который вероятно отличается от . Общепринятый метод вычисления несоответствия между ожидаемым и получившимся ответом — квадратичная функция потерь:
- где ошибка.
В качестве примера, обучим сеть на объекте , таким образом, значения и равны 1, а равно 0. Построим график зависимости ошибки от действительного ответа , его результатом будет парабола. Минимум параболы соответствует ответу , минимизирующему . Если тренировочный объект один, минимум касается горизонтальной оси, следовательно ошибка будет нулевая и сеть может выдать ответ равный ожидаемому ответу . Следовательно, задача преобразования входных значений в выходные может быть сведена к задаче оптимизации, заключающейся в поиске функции, которая даст минимальную ошибку.
График ошибки для нейрона с линейной функцией активации и одним тренировочным объектом
В таком случае, выходное значение нейрона — взвешенная сумма всех его входных значений:
где и — веса на ребрах, соединяющих входные вершины с выходной. Следовательно, ошибка зависит от весов ребер, входящих в нейрон. И именно это нужно менять в процессе обучения. Распространенный алгоритм для поиска набора весов, минимизирующего ошибку — градиентный спуск. Метод обратного распространения ошибки используется для вычисления самого «крутого» направления для спуска.
Дифференцирование для однослойной сети
Метод градиентного спуска включает в себя вычисление дифференциала квадратичной функции ошибки относительно весов сети. Обычно это делается с помощью метода обратного распространения ошибки. Предположим, что выходной нейрон один, (их может быть несколько, тогда ошибка — это квадратичная норма вектора разницы) тогда квадратичная функция ошибки:
- где — квадратичная ошибка, — требуемый ответ для обучающего образца, — действительный ответ сети.
Множитель добавлен чтобы предотвратить возникновение экспоненты во время дифференцирования. На результат это не повлияет, потому что позже выражение будет умножено на произвольную величину скорости обучения (англ. learning rate).
Для каждого нейрона , его выходное значение определено как
Входные значения нейрона — это взвешенная сумма выходных значений предыдущих нейронов. Если нейрон в первом слое после входного, то входного слоя — это просто входные значения сети. Количество входных значений нейрона . Переменная обозначает вес на ребре между нейроном предыдущего слоя и нейроном текущего слоя.
Функция активации нелинейна и дифференцируема. Одна из распространенных функций активации — сигмоида:
у нее удобная производная:
Находим производную ошибки
Вычисление частной производной ошибки по весам выполняется с помощью цепного правила:
Только одно слагаемое в зависит от , так что
Если нейрон в первом слое после входного, то — это просто .
Производная выходного значения нейрона по его входному значению — это просто частная производная функции активации (предполагается что в качестве функции активации используется сигмоида):
По этой причине данный метод требует дифференцируемой функции активации. (Тем не менее, функция ReLU стала достаточно популярной в последнее время, хоть и не дифференцируема в 0)
Первый множитель легко вычислим, если нейрон находится в выходном слое, ведь в таком случае и
Тем не менее, если произвольный внутренний слой сети, нахождение производной по менее очевидно.
Если рассмотреть как функцию, берущую на вход все нейроны получающие на вход значение нейрона ,
и взять полную производную по , то получим рекурсивное выражение для производной:
Следовательно, производная по может быть вычислена если все производные по выходным значениям следующего слоя известны.
Если собрать все месте:
и
Чтобы обновить вес используя градиентный спуск, нужно выбрать скорость обучения, . Изменение в весах должно отражать влияние на увеличение или уменьшение в . Если , увеличение увеличивает ; наоборот, если , увеличение уменьшает . Новый добавлен к старым весам, и произведение скорости обучения на градиент, умноженный на , гарантирует, что изменения будут всегда уменьшать . Другими словами, в следующем уравнении, всегда изменяет в такую сторону, что уменьшается:
Алгоритм
- — скорость обучения
- — коэффициент инерциальности для сглаживания резких скачков при перемещении по поверхности целевой функции
- — обучающее множество
- — количество повторений
- — функция, подающая x на вход сети и возвращающая выходные значения всех ее узлов
- — количество слоев в сети
- — множество нейронов в слое i
- — множество нейронов в выходном слое
fun BackPropagation:
init
repeat :
for = to :
=
for :
=
for = to :
for :
=
for :
=
=
return
Недостатки алгоритма
Несмотря на многочисленные успешные применения обратного распространения, оно не является универсальным решением. Больше всего неприятностей приносит неопределённо долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.
Градиентный спуск может найти локальный минимум вместо глобального
Паралич сети
В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших выходных значениях, а производная активирующей функции будет очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть.
Локальные минимумы
Градиентный спуск с обратным распространением ошибок гарантирует нахождение только локального минимума функции; также, возникают проблемы с пересечением плато на поверхности функции ошибки.
Примечания
- Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
- Neural Nets
- Understanding backpropagation
См. также
- Нейронные сети, перцептрон
- Стохастический градиентный спуск
- Настройка глубокой сети
- Практики реализации нейронных сетей
Источники информации
- https://en.wikipedia.org/wiki/Backpropagation
- https://ru.wikipedia.org/wiki/Метод_обратного_распространения_ошибки
Оглавление:
- Что такое искусственные нейронные сети?
- Виды обучения нейронных сетей
- Многослойные нейронные сети и их базовые понятия
- Разбираемся на примере
- Заключение
Что такое искусственные нейронные сети?
Данная статья предназначена для ознакомления читателя с искусственными нейронными сетями (далее ANN – Artificial Neural Network) и базовыми понятиями многослойных нейронных сетей.
Основным элементом ANN является нейрон. Его основной задачей является перемножение предыдущих значений нейронов или входных значений с соответствующими им весовыми коэффициентами связей между соответствующими нейронами, после активации вычисленного значения.
Основными задачами ANN является классификация, принятие решения, анализ данных, прогнозирование, оптимизация.
Искусственные нейронные сети категорируются по топологии (полносвязные, многослойные, слабосвязные), способу обучения (с учителем, без учителя, с подкреплением), модели нейронной сети (прямого распространения, рекррентные нейронные сети, сверточные нейронные сети, радиально-базисные функции), а также по типу связей (полносвязные, многослойные, слабосвязные). Такой значительно большой тип категорирования связан с разнообразием задач, которые ставятся перед ANN. Примеры, приведенные в скобках являются одними из самых распространенных типов категорирования, на самом деле их значительно больше.
Виды обучения нейронных сетей
Обучение с учителем
Данный тип обучения является самым простым, за счет того, что нет необходимости в написании алгоритмов самообучения. Для обучения с учителем требуется размеченный и структурированный набор данных для обучения. Под словом «размеченный» подразумевается процесс обозначения верного ответа на конкретный набор входных данных, который мы ожидаем от нейронной сети как результат работы. За счет таких данных нейронная сеть будет ориентироваться на разметку и корректировать процесс обучения за счет определения совершенных ошибок, которые будут определяться из данных разметки и ее предсказанных данных.
Обучение без учителя
Под обучением без учителя подразумевается процесс обучения нейронной сети без какого-либо контроля с нашей стороны. Весь процесс будет протекать за счет нахождения нейронной сетью корреляции в данных, извлечения полезных признаков и их анализа.
Существуют несколько способов обучения без учителя: обнаружение аномалий, ассоциации, автоэнкодеры и кластеризация.
На основе алгоритмов, описанных выше, в процессе обучения будет определяться значение ошибки, допущенной на каждом шаге обучения, за счет чего будет происходить корректировка обучения, следовательно, нейронная сеть обучится. За счет наличия алгоритмов, процесс написания которых занимает много времени и сильно усложняет моделирование нейронной сети, данный тип обучения считается самым сложным.
Обучение с подкреплением
Обучение с подкреплением или частичным вмешательством учителя можно считать золотой серединой в обучении нейронных сетей. Данный тип обучения представляет собой обучение без учителя с периодической его корректировкой. Корректировка обучения происходит тогда, когда нейронная сеть допускает ошибки при обучении.
Многослойные нейронные сети и их базовые понятия
Каждая ANN имеет входной, выходной и скрытые слои. Количество скрытых слоев и их сложность (количество искусственных нейронов) зачастую играют важную роль в процессе обучения, обеспечивая хорошее обучение модели нейронной сети.
Многослойными ANN называются нейронные сети, у которых количество скрытых слоев более одного. Пример многослойной нейронной сети:
Входной, выходной и скрытые слои, нормализация и зачем все это нужно?
Входной слой дает возможность «скормить» данные, на которых требуется производить обучение. Выходной, в свою очередь, выдает результат работы нейронной сети. Вся суть заключается в скрытых слоях. Повторюсь, количество скрытых слоев и их сложность определяют качество обучения. Объясню на простом примере. Я, при написании модели нейронной сети, которая классифицирует рукописные цифры, смоделировал нейронную сеть из двух скрытых слоев по 30 нейронов в каждом. На вход подавал изображение 28х28 пикселей, но предварительно проведя нормализацию (объясню чуть ниже) входных значений и приведение изображения к виду 784х1, путем расставления всех столбцов в один. Т.е. входными значениями являлись 0 и 1, а если быть точнее — значения из данного диапазона. Так вот эти 0 и 1 оказались на входном слое, т.е. каждый нейрон входного слоя представлял из себя пиксель исходного изображения. Далее следовал скрытый слой, состоящий из 30 нейронов. Так вот, эти 30 нейронов представляют собой 30 участков исходного изображения, а каждый участок в свою очередь содержит какие-либо признаки, характеризующие изображение как определенную цифру. Т.е. чем больше нейронов в скрытых слоях, тем точнее будет представление и градуировка исходного изображения. Будет «плодиться» больше характеристик, по которым нейронная сеть будет классифицировать изображение должным образом.
Вернусь к такому понятию, как нормализация. Она необходима для приведения входных значений к значениям из диапазона 0 и 1. Смысл заключается в том, что нейронная сеть должна явно или с долей вероятности классифицировать изображение, или дать какое-то предсказание. Раз предсказание представляет собой вероятность, то и входные значения должны быть в диапазоне от 0 до 1. Поэтому нормализация, к примеру, значений пикселей изображения, происходит путем деления на 255, т.к. значения пикселей находятся в диапазоне от 0 до 255 и максимальным значением является значение 255.
Весовые коэффициенты
Каждая связь между искусственными нейронами обладает весовым коэффициентом, который постоянно изменяется в процессе обучения и является величиной, которая увеличивает или уменьшает предсказанную вероятность. К примеру, при уменьшении веса связи между 1 и 2 нейроном и увеличении веса между 1 и 3 получим, что, используя сигмоидальную функцию активации, значение на ее выходе в 1-ом случае будет стремиться к 0, а во втором к 1. Т.е. весовые коэффициенты являются своего рода возбудителями искусственных нейронов к прогнозированию.
Функция активация, виды и особенности
Функция активации является нормализующим звеном на каждом слое нейронной сети. Она представляет из себя функцию, которая приводит входное значение к значению от 0 до 1. Одной из самых распространенных функция активации является сигмоидальная функция активации:
Значение ‘х’ является значением, которое обрабатывается функцией активации. Оно включает в себя алгебраическую сумму произведений значений нейронов на предыдущем слое на соответствующие им связи с тем нейроном, на котором мы производим расчет функции активации, а также нейрон смещения.
Пример вычисления функции активации приведен на рис. 5
Распространенные виды функций активации:
- Активация пороговой функции; функция активирована, если x, не активирована, если х<0
- Гиперболическая касательная функция ошибки; функция нелинейна, ее значения находятся в диапазоне (-1;1)
- ReLu и LeakyReLu; функция ReLu равна при х, при x, а при х<0 равна 0. Отличием LeakyReLu от ReLu является наличие коэффициента, определяющего значение функции при х<0 как ах
Функция ошибки, виды
Функция ошибки необходима для определения ошибки прогнозирования, допускаемой нейронной сетью на каждом этапе обучения и корректировкой процесса обучения, за счет корректировки весовых значений связей между искусственными нейронами.
Примеры функций ошибок:
- Кросс-энтропия
- Квадратичная (среднеквадратичное отклонение)
- Расстояние Кульбака — Лейблера
- Экспоненциальная
Самая простая и часто используемая функция ошибок (функция потерь) – среднеквадратичное отклонение.
Она вычисляется как половина от алгебраической суммы квадрата разности, прогнозируемого нейронной сетью значения и реальным значением – разметкой данных.
Backpropagation или обратное распространение ошибки
Для корректировки весов на каждом слое нейронной сети необходима метрика для определения ошибки каждого веса, с этой целью был разработан алгоритм обратного распространения ошибки. Он работает следующим образом:
- Вычисляется прогнозируемое нейронной сетью значение на выходе ANN
- Производится расчет функции ошибки, к примеру, среднеквадратичной
- Корректируются веса связей нейронов на последнем слое на основе вычисленной ошибки на выходе
- Происходит расчет ошибки на предпоследнем слое нейронной сети на основании скорректированных весов связей на последнем слое и ошибки на выходе ANN
- Процесс повторяется до первого слоя нейронной сети
Пример работы алгоритма обратного распространения ошибки:
Bias или нейрон смещения
Значение смещения позволяет сместить функцию активации влево или вправо, что может иметь решающее значение для успешного обучения, а также позволяет быть более гибким при выборе решения или прогнозировании.
При наличии нейрона смещения, его значение тоже поступает на вход функции активации, складываясь с алгебраической суммой произведений нейронов и их весовых коэффициентов.
Пример работы нейрона смещения:
Разбираемся на примере
В данном примере напишем классификатор рукописных цифр на языке программирования С++. Обучающую выборку найдем на официальном сайте MNIST.
В первую очередь импортируем модули:
Определим обучающую выборку ‘dataset’, и загрузим в нее размеченные изображения MNIST.
Создадим входной слой равный 784 нейронам, так как наши изображения равны 28х28 пикселей и мы разложим их в цепочку пикселей 784х1, чтобы подать на вход нейронной сети; два скрытых слоя размера 30 нейронов каждый (размеры скрытых слоев подбирались случайно); выходной слой размером 10 нейронов, так как наша нейросеть будет классифицировать числа в диапазоне 0-9, где первый нейрон будет отвечать за классификацию числа 0, второй за число 1 и так далее до 9.
Необходимо сразу инициализировать наши значения слоев, к примеру 0.
Создадим матрицы весов между входным и 1-м скрытым слоями, 1-м скрытым и 2-м скрытым слоями, 2-м скрытым и выходным слоями, и инициализируем матрицы случайными значениями, как показано на рисунке. На примере значения весов находятся в диапазоне [-1;1].
Также необходимо создать массивы, которые будут содержать в себе значения алгебраической суммы произведения весов на соответствующие нейроны, как было описано выше в статье, после чего эти значения будут подаваться в функцию активации.
Ниже были созданы массивы ошибок на каждом слое. Для сохранения результатов ошибок на каждом нейроне, были инициализированы количество эпох и скорость обучения (определяет скорость перемещения по функции в поисках минимума во время обучения; необходимо быть осторожным с этим значением, так как если оно будет слишком мало, то, есть вероятность остаться в локальном минимуме, не найдя настоящий минимум функции или наоборот, при слишком большом значении, есть вероятность перескочить главный минимум функции.)
На данном этапе начинается процесс обучения нашей нейронной сети. Внешний цикл определяет количество эпох обучения, а внутренний количество итераций обучения в каждой эпохе.
На рисунке ниже инициализируются значения из обучающей выборки MNIST и занесения их на входной слой нейронной сети, а после происходит инициализация S-величин, о которых было сказано выше, нулями
Ниже происходит подсчет алгебраической суммы значений произведений веса на соответствующий нейрон, а после прохождение их через функцию активации, где в роли функции активации выступает сигмоидальная функция.
Подсчитав значения на каждом слое, происходит инициализация массивов ошибок, путем заполнения их 0, а также определение ошибок на выходном слое, путем вычитания полученных значений из 1, и последующим умножением на произведение значений нейронов прошедших через функцию активации на выходном слое на разницу между 1 и этими же значениями.
Далее необходимо определить ошибки на каждом слое нейронной сети методом обратного распространения ошибки. К примеру, чтобы найти ошибку на первом нейроне предыдущего слоя от выходного слоя, необходимо найти алгебраическую сумму произведения ошибок нейронов на выходном слое на соответствующие им веса связей с первым нейроном предыдущего слоя и перемножить на произведение значения нейронов на предпоследнем слое на разницу 1 и этих же значений. Таким образом необходимо найти допущенные ошибки нейронной сетью на каждом слое.
После определения ошибок, допущенных нейронной сетью на каждом нейроне, приступаем к корректировке весовых коэффициентов связей между каждым нейроном. Алгоритм корректировки представлен ниже.
Скорректировав веса, определяем максимальное полученное значение на выходном слое, тем самым определим ответ нейронной сети после прохождения через нее изображения.
Заключение
В этой статье мы разобрались с базовыми понятиями искусственных нейронных сетей, а именно с такими как: входной, выходной, скрытые слои и их предназначение, весовыми коэффициентами связи между искусственными нейронами, функцией активации и ее предназначением, методами определения ошибки на каждом искусственном, с понятием нейрона смещения и функциями ошибки. В следующей статье мы перейдем к изучению нового класса нейронных сетей, таких как сверточные нейронные сети (CNN).
Желаю всем успехов в изучении!
Метод обратного распространения ошибки — метод обучения многослойного перцептрона. Впервые метод был описан в 1974 г. Полем Дж. Вербосом[1], а также независимо и одновременно А. И. Галушкиным[2]. Далее существенно развит в 1986 г. Дэвидом И. Румельхартом, Дж. Е. Хинтоном и Рональдом Дж. Вильямсом[3] и независимо и одновременно С. И. Барцевым и В. А. Охониным (Красноярская группа)[4]. Это итеративный градиентный алгоритм, который используется с целью минимизации ошибки работы многослойного перцептрона и получения желаемого выхода.
Основная идея этого метода состоит в распространении сигналов ошибки от выходов сети к её входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Барцев и Охонин предложили сразу общий метод («принцип двойственности»), приложимый к более широкому классу систем, включая системы с запаздыванием, распределённые системы, и т. п.[5]
Для возможноcти применения метода обратного распространения ошибки передаточная функция нейронов должна быть дифференцируема.
Cигмоидальные функции активации[]
Наиболее часто в качестве функций активации используются следующие виды сигмоид:
Функция Ферми (экспоненциальная сигмоида):

Рациональная сигмоида:
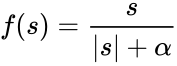
Гиперболический тангенс:
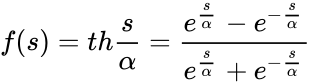
где s — выход сумматора нейрона, 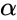
Менее всего, сравнительно с другими сигмоидами, процессорного времени требует расчет рациональной сигмоиды. Для вычисления гиперболического тангенса требуется больше всего тактов работы процессора. Если же сравнивать с пороговыми функциями активациями, то сигмоиды расчитываются очень медленно. Если после суммирования в пороговой функции сразу можно начинать сравнение с определенной величиной (порогом), то в случае сигмоидальной функции активации — нужно расчитать сигмоид (затратить время в лучшем случае на три операции: взятие модуля, сложение и деление), и только потом сравнивать с пороговой величиной (например, нулем). Если считать, что все простейшие операции расчитываются процессором за примерно одинаковое время, то работа сигмоидальной функции активации после произведенного суммирования (которое займет одинаковое время) будет медленее пороговой функции активации как 1:4.
Функция оценки работы сети[]
В тех случаях, когда удается оценить работу сети обучение нейронных сетей можно представить как задачу оптимизации. Оценить — означает указать количественно хорошо или плохо сеть решает поставленные ей задачи. Для этого строится функция оценки. Она, как правило, явно зависит от выходных сигналов сети и неявно (через функционирование) — от всех ее параметров. Простейший и самый распространенный пример оценки — сумма квадратов расстояний от выходных сигналов сети до их требуемых значений:

где 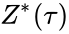
Метод наименьших квадратов далеко не всегда является лучшим выбором оценки. Тщательное конструирование функции оценки позволяет на порядок поысить эффективность обучения сети, а также получать дополнительную информацию — «уровень уверенности» сети в даваемом ответе[6].
Описание алгоритма[]
Файл:Neuro.PNG
Архитектура многослойного перцептрона
Алгоритм обратного распространения ошибки применяется для многослойного перцептрона. У сети есть входы 
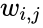
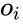
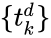
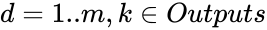

Как модифицировать веса? Мы будем реализовывать стохастический градиентный спуск, то есть будем подправлять веса после каждого тестового примера. Нам нужно двигаться в сторону, противоположную градиенту, то есть добавлять к каждому весу 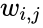
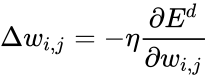
где
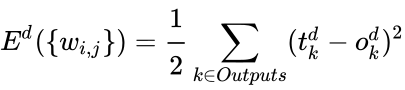
Производная считается следующим образом. Пусть сначала 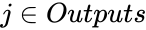
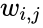
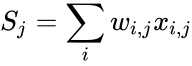

Аналогично, 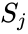
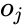
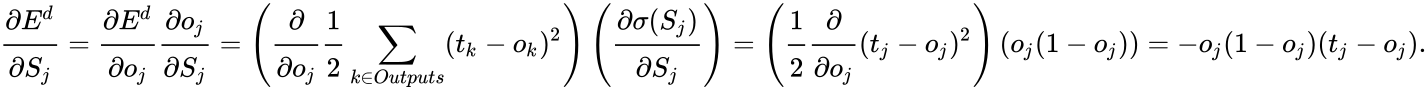
Если же j-й узел — не на последнем уровне, то у него есть выходы; обозначим их через Children(j). В этом случае

и

Ну а 
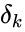
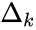
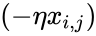
поправок алгоритм называется алгоритмом обратного распространения ошибки (backpropagation). Краткое резюме проделанной работы:
- для узла последнего уровня

- для внутреннего узла сети

- для всех узлов
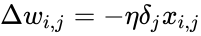
Получающийся алгоритм представлен ниже. На вход алгоритму, кроме указанных параметров, нужно также подавать в каком-нибудь формате структуру сети. На практике очень хорошие результаты показывают сети достаточно простой структуры, состоящие из двух уровней нейронов — скрытого уровня (hidden units) и нейронов-выходов (output units); каждый вход сети соединен со всеми скрытыми нейронами, а результат работы каждого скрытого нейрона подается на вход каждому из нейронов-выходов. В таком случае достаточно подавать на вход количество нейронов скрытого уровня.
Алгоритм[]
Алгоритм:
BackPropagation 
- Инициализировать
маленькими случайными значениями.
- Повторить NUMBER_OF_STEPS раз:
- Для всех d от 1 до m:
- Подать
на вход сети и подсчитать выходы
каждого узла.
- Для всех
.
- Для каждого уровня l, начиная с предпоследнего:
- Для каждого узла j уровня l вычислить
.
- Для каждого ребра сети {i, j}
.
- Выдать значения
.
Математическая интерпретация обучения нейронной сети[]
На каждой итерации алгоритма обратного распространения весовые коэффициенты нейронной сети модифицируются так, чтобы улучшить решение одного примера. Таким образом, в процессе обучения циклически решаются однокритериальные задачи оптимизации.
Обучение нейронной сети характеризуется четырьмя специфическими ограничениями, выделяющих обучение нейросетей из общих задач оптимизации: астрономическое число параметров, необходимость высокого параллелизма при обучении, многокритериальность решаемых задач, необходимость найти достаточно широкую область, в которой значения всех минимизируемых функций близки к минимальным. В остальном проблему обучения можно, как правило, сформулировать как задачу минимизации оценки. Осторожность предыдущей фразы («как правило») связана с тем, что на самом деле нам неизвестны и никогда не будут известны все возможные задачи для нейронных сетей, и, быть может, где-то в неизвестности есть задачи, которые несводимы к минимизации оценки. Минимизация оценки — сложная проблема: параметров астрономически много (для стандартных примеров, реализуемых на РС — от 100 до 1000000), адаптивный рельеф (график оценки как функции от подстраиваемых параметров) сложен, может содержать много локальных минимумов.
Недостатки алгоритма[]
Несмотря на многочисленные успешные применения обратного распространения, оно не является панацеей. Больше всего неприятностей приносит неопределенно долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.
Паралич сети[]
В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших значениях OUT, в области, где производная сжимающей функции очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть. В теоретическом отношении эта проблема плохо изучена. Обычно этого избегают уменьшением размера шага η, но это увеличивает время обучения. Различные эвристики использовались для предохранения от паралича или для восстановления после него, но пока что они могут рассматриваться лишь как экспериментальные.
Локальные минимумы[]
Обратное распространение использует разновидность градиентного спуска, то есть осуществляет спуск вниз по поверхности ошибки, непрерывно подстраивая веса в направлении к минимуму. Поверхность ошибки сложной сети сильно изрезана и состоит из холмов, долин, складок и оврагов в пространстве высокой размерности. Сеть может попасть в локальный минимум (неглубокую долину), когда рядом имеется гораздо более глубокий минимум. В точке локального минимума все направления ведут вверх, и сеть неспособна из него выбраться. Статистические методы обучения могут помочь избежать этой ловушки, но они медленны.
Размер шага[]
Внимательный разбор доказательства сходимости[3] показывает, что коррекции весов предполагаются бесконечно малыми. Ясно, что это неосуществимо на практике, так как ведет к бесконечному времени обучения. Размер шага должен браться конечным, и в этом вопросе приходится опираться только на опыт. Если размер шага очень мал, то сходимость слишком медленная, если же очень велик, то может возникнуть паралич или постоянная неустойчивость. П. Д. Вассерман[7] описал адаптивный алгоритм выбора шага, автоматически корректирующий размер шага в процессе обучения. В книге А. Н. Горбаня[8] предложена разветвлённая технология оптимизации обучения.
См. также[]
- Сигмоид
- Многослойный перцептрон
Литература[]
- Уоссермен Ф. Нейрокомпьютерная техника: Теория и практика. — М.: «Мир», 1992.
- Хайкин С. Нейронные сети: Полный курс. Пер. с англ. Н. Н. Куссуль, А. Ю. Шелестова. 2-е изд., испр. — М.: Издательский дом Вильямс, 2008, 1103 с.
Внешние ссылки[]
- Копосов А.И., Щербаков И.Б., Кисленко Н.А., Кисленко О.П., Варивода Ю.В. и др. Отчет по научно-исследовательской работе «Создание аналитического обзора информационных источников по применению нейронных сетей для задач газовой технологии». — Москва: ВНИИГАЗ, 1995.
- Миркес Е. М., Нейроинформатика: Учеб. пособие для студентов с программами для выполнения лабораторных работ. Красноярск: ИПЦ КГТУ, 2002, 347 с. Рис. 58, табл. 59, библиогр. 379 наименований. ISBN 5-7636-0477-6
Примечания[]
- ↑ Werbos P. J., Beyond regression: New tools for prediction and analysis in the behavioral sciences. Ph.D. thesis, Harvard University, Cambridge, MA, 1974.
- ↑ Галушкин А. И. Синтез многослойных систем распознавания образов. — М.: «Энергия», 1974.
- ↑ 3,0 3,1 Rumelhart D.E., Hinton G.E., Williams R.J., Learning Internal Representations by Error Propagation. In: Parallel Distributed Processing, vol. 1, pp. 318—362. Cambridge, MA, MIT Press. 1986.
- ↑ Барцев С. И., Охонин В. А. Адаптивные сети обработки информации. Красноярск : Ин-т физики СО АН СССР, 1986. Препринт N 59Б. — 20 с.
- ↑ Барцев С. И., Гилев С. Е., Охонин В. А., Принцип двойственности в организации адаптивных сетей обработки информации, В кн.: Динамика химических и биологических систем. — Новосибирск: Наука, 1989. — С. 6-55.
- ↑ Миркес Е. М., — Новосибирск: Наука, Сибирская издательская фирма РАН, 1999. — 337 с. ISBN 5-02-031409-9 Другие копии онлайн: [1]
- ↑ Wasserman P. D. Experiments in translating Chinese characters using backpropagation. Proceedings of the Thirty-Third IEEE Computer Society International Conference.. — Washington: D. C.: Computer Society Press of the IEEE, 1988.
- ↑ Горбань А. Н. Обучение нейронных сетей.. — Москва: СП ПараГраф, 1990.
ОРО и корректировка весов в нейросети
Ранее мы улучшали поведение простого линейного классификатора и рассмотрели, как по входу и матрицам весов нейросети вычислить её выход.
Теперь предположим, что имеется некий эталоный выход, к которому должен стремиться результат работы нейросети. Для достижения эталона нам потребуется что-то перенастраивать в сети. Это будут весовые коэффициенты.
Выясним, как мы будем обновлять матрицы весов.
Заготовка распределения ошибки. Изображение из (1)
Обратное распространение ошибки в нейронной сети
Воспользуемся методом ОРО, пропорционально распределяя ошибку между имеющимися узлами:
Простая сеть и ошибка на узлах. Изображение из (1)
Определим ошибку на выходном слое ( e^{О}), как разность между эталонным значением ( t_{i}) и полученным ( o_{i}) на выходе нейросети :
( e^{О}_{i} = t_{i} — o_{i})
Тогда, глядя на рисунок выше, заключим, что ошибка ( e^{О}_{1}) распределяется пропорционально весам ( w_{11}) и ( w_{21}), а ошибка ( e^{О}_{2}) должна распределяться пропорционально весам ( w_{12}) и ( w_{22}).
Запишем эти доли в явном виде:
( e^{O}_{1} = displaystylefrac {w_{11}}{w_{11} + w_{21}}; quad e^{O}_{2} = displaystylefrac {w_{12}}{w_{12} + w_{22}}, )
Итак, на основе отклонения текущего выхода от эталонного, мы будем обновлять весовые коэффициенты во всей нейросети, двигаясь с конца к её началу.
Распределение ошибки по слоям. Изображение из (1)
Но если сначала мы использовали ошибку выходного слоя, то какую ошибку использовать для узлов скрытого слоя? Ведь мы не можем указать очевидную ошибку для узла в таком слое.
Разберёмся, как определить ошибку для скрытого узла.
Ошибка скрытого слоя
Мы можем воссоединить ошибки, распределенные по связям следующим образом: ошибка на первом скрытом узле ( e^{H}_{1} ) представляет собой сумму ошибок, распределенных по всем связям, исходящим из этого узла в прямом направлении:
( e^{H}_{1} = e^{O}_{1} cdot frac {w_{11}}{w_{11} + w_{21}} + e^{O}_{2} cdot frac {w_{12}}{w_{12} + w_{22}}, )
или как показано на иллюстрации ниже:
Метод ОРО. Изображение из (1)
Применять данную методику мы будем до тех пор, пока не доберёмся до входного слоя:
Расчет ошибки на внутренних узлах. Изображение из (1)
Векторизация метода ОРО в нейросети
Опять, так как Scilab — матричный язык, адаптируем поэлементный процесс обратного распространения ошибки в нейросети под удобный нам.
Зададим эталонный вектор ( V_{e}), тогда ошибка ( E_O) на выходном слое ( O) считается самым простым способом:
( E_O = V_{e} — O )
Ошибка ( E_H ) на скрытом слое ( H) будет считаться с учетом вклада каждого узла следующим образом:
( E_H = begin{pmatrix}
frac {w_{11}}{w_{11} + w_{21}} & frac {w_{12}}{w_{12} + w_{22}}
frac {w_{21}}{w_{21} + w_{11}} & frac {w_{22}}{w_{22} + w_{12}}
end{pmatrix} cdot E_o
)
Здесь ( w_{ij} ) — элементы матрицы ( W_{HO} ), задающей веса для слоёв выходной-скрытый.
Это выражение можно переписать в более простом виде, отказавшись от знаменателей в первом множителе. Тогда получим связь с весовой матрицей на текущем шаге:
( E_H = begin{pmatrix}
w_{11} & w_{12}
w_{21} & w_{22}
end{pmatrix} cdot E_O
)
Итак, ошибка ( E_H ) скрытого вычисляется с учётом ошибки (E_O) выходного слоя и матрицы ( W_{HO} ):
( E_H = W_{HO}^T cdot E_O)
Аналогично, для входного слоя ошибка ( E_I ) будет вычисляться с учётом ошибки (E_H) предыдущего слоя в связи с матрицей ( W_{IH} ), определяющей веса входной-скрытый слоёв:
( E_I = W_{IH}^T cdot E_H)
Обновление весовых коэффициентов
Для обновления весовых коэффициентов мы воспользуемся методом градиентного спуска (подробнее в (1)).
При подсчёте ошибки на каждом из слоёв, будем немного корректировать весовые коэффициенты соответвующей весовой матрицы на величину ( Delta w ), которая на векторно-матричном языке может быть представлена как:
( Delta w = — alpha cdot E_k cdot O_k cdot (1 — O_k) cdot O^T_j, )
где
(alpha — ) скорость обучения нейронной сети (alpha in (0,1) ),
(E_k — ) ошибка текущего слоя (вектор столбец),
(O_k — ) текущий слой (вектор-столбец),
(O^T_j — ) предыдущий слой (вектор-столбец).
А обновлённая матрица весов примет вид:
( W^{new} = W^{cur} — Delta w )
Осталось лишь собрать всё в программный код обучения нейросети 😁
Данная статья создана на основе чудесной книги(1) с реализацией автором приведённых примеров на Scilab.
Интерес к нейронным сетям
Анализируя посещаемость нашего сайта, мы видим колоссальный интерес читателей к нейронным сетям. Данный инструментарий может решать целый набор задач, в том числе, прогнозировать временные ряды весьма эффективно. В частности, в своей диссертации я пишу следующим образом.
— В ряде работ [2],[36],[37] указано, что на сегодняшний день наиболее распространенными моделями прогнозирования являются авторегрессионные модели (ARIMAX), а также нейросетевые модели (ANN). В статье [3], в частности, утверждается: «Without a doubt ARIMA(X) and GRACH modeling methodologies are the most popular methodologies for forecasting time series. Neural networks are now the biggest challengers to conventional time series forecasting methods».
— Без сомнений модели ARIMA(X) и GARCH являются самыми популярными для прогнозирования временных рядов. В настоящее время главную конкуренцию данным моделям составляют модели на основе ANN.
У нас на сайте пока опубликован только один материал, посвященный нейронным сетям, в котором я давала советы по созданию сети. Интерес со стороны читателей заставляет меня более активно заниматься нейросетевым прогнозированием. Давайте попробуем шаг за шагом проделать работу по созданию, эффективному обучению и адаптации нейронной сети с тем, чтобы разобраться в нюансах нейросетевых моделей прогнозирования.
Первая нейронная сеть
Не стоит изобретать велосипед, а стоит взять готовый пример из книги Хайкина. Сама задача и ее решение подробно описаны в разделе 4.8 данной книги. Полный архив примеров для книги выложен у нас на форуме. Отдельно взятый рабочий пример можно скачать в архиве. Главный файл называется Create_ANN_step_0.m.
Приведенная программа решает задачу классификации. Прокомментирую текст основного файла.
% 1. Формирование исходного массива данных P=mk_data(500); % 2. Обучение нейронной сети по методу % Back Propagation Error (обратное распространение ошибки) [W1, b1, W2, b2, ep_err, a, end_ep]=... bpm_train(P, 4, 2, 2, .1, .5, 500, 0,0,0,0,0); % 3. Проверка граничных значений bpm_dec_bnds(W1, b1, W2, b2, .1); % 4. Формирование тестового массива T=mk_data(10000); % 5. Проверка созданной сети на тестовом массиве [cor, uncor]=bpm_test(W1,b1,W2,b2,T); % 6. Построение графика c=pl_circ([-2/3 0], 2.34, .01, 1);
Прогнозирование с помощью нейронной сети
Я взяла данный пример реализации нейронной сети, просмотрела внимательно содержание его функций и сделала свою нейронную сеть, которая прогнозирует торговый график по европейской территории РФ (далее ТГ) на 24 значения вперед. В архиве вы можете скачать, как полученный мною пример, так и исходные данные к нему. Основной файл называется Create_ANN_step_1.m
Шаг 1. Инициализация и исходные данные
Исходные данные по торговому графику содержатся в файле VOLUMES_EUR.mat и имеют значения за период с 01.09.2006 до 22.11.2011.
Обучение сети, то есть определение весов и смещений для всех нейронов я выполняю на периоде значений с 01.01.2010 по 31.12.2010.
В качестве тестового я выбрала период с 01.01.2011 по 22.11.2011.
Шаг 2. Предварительная обработка исходных данных
Из теории и из примера Хайкина я понимаю, что нейронная сеть работает со значениями временных рядов от 0 до 1. Исходные значения торгового графика в массиве VOLUMES_EUR, конечно, выходят далеко за этот диапазон. Для использования нейронной сети необходимо предварительно отмасштабировать исходный временной ряд, как показано на рисунках.
Рис 1. Предварительно мы имели значения от 57 847 до 111 720.
Рис 2. После масштабирования мы стали иметь значения от 0 до 1.
Шаг 3. Настройка нейронной сети
Так как в примере Хайкина содержалась трехслойная полносвязная нейронная сеть, то я на ней остановилась. Кроме того, из статей я знаю, что для прогнозирования энергопотребления чаще других используется именно трехслойная архитектура.
На вход нейронной сети я подаю 48 значений ТГ за двое предыдущих суток, скрытый слой после нескольких попыток стал содержать 72 нейрона, а на выходе мы получаем 24 прогнозных значений торгового графика на будущие сутки. Структура нейронной сети получилась следующая.
Рис 3. Структура разработанной нейронной сети.
После описания структуры указываются значения нескольких параметров нейронной сети (см файл Create_ANN_step_1.m). Не мудрствуя лукаво, оставила все значения, которые были установлены в примере Хайкина.
Шаг 4. Обучение сети
Двойной цикл по эпохам и внутренней корректировки весов я взяла в чистом виде из примера Хайкина. Такое обучение называется обучением нейронной сети по методу back propagation error (обратное распространение ошибки). Изменения внесены только в части формирования входа и выхода нейронной сети. Общие комментарии по ходу алгоритма приведены в тексте программы.
Шаг 5. Тестовое прогнозирование
На пятом шаге я формирую тестовый массив «T» и прогнозирую на полученной нейронной сети. Все прогнозирование в итоге сходится к нескольким строчкам кода.
% Вход i1 = T([(i-1)*24+1:i*24],2); i2 = T([(i-1)*24+1:i*24],3); input = [i1; i2]; % Прогноз outHiddenLayer = bpm_phi(W1 * input + b1); outOutputLayer = bpm_phi(W2 * outHiddenLayer + b2); % Переменная результата Result([(i-1)*24+1:i*24],1) = outOutputLayer;
По результатам прогноза я провожу инверсию масштаба.
Шаг 6. Оценка ошибки прогнозирования
На последнем шаге я вычисляю значения ошибки прогнозирования временных рядов MAE и MAPE.
Величина MAPE оставила около 4%, что показывает в целом адекватность разработанной нейросетевой модели прогнозирования. Однако мы знаем, что это далеко не предел точности! Аналогичное значение MAPE для того же самого временного ряда в отчете за аналогичный период (за 2011 год) составляет около 1.18% при использовании нашей внутренней модели прогнозирования. Подробности можно посмотреть в отчете Точность прогнозирования за истекшие периоды. В упомянутом отчете временной ряд назван для краткости ТГ ЕЦЗ (торговый график европейской ценовой зоны).
Результаты
Переделав пример Хайкина под нужны прогнозирования торгового графика (энергопотребления), мы получили новую нейронную сеть, трехслойную, полносвязную. Все параметры сети были из примера по книге Хайкина.
Созданная нейронная сеть обучается очень быстро: от 60 до 120 секунд в зависимости от мощности компьютера.
При тестовом прогнозировании на созданной нейронной сети получается прогноз торгового графика на сутки вперед с ошибкой MAPE ≅ 4%.
Исходный пример из книги Хайкина, а также мой пример нейронной сети для прогнозирования торгового графика европейской территории РФ с исходными данными вы можете скачать по приведенным ссылкам и попробовать решить свою задачу.
UPD 02.02.2016.
Уважаемые читатели, если вы скачали пример и пытаетесь на скорую руку прикрутить его к своей задаче, то обращаю ваше внимание на следующее.
- Если вы потратили меньше чем 6 месяцев на эти работы, то не ждите никакого адекватного результата. И полгода на приличный результат мало!
- Если у вас возник вопрос вроде «а где в коде то и се?», то имейте в виду, что я не буду впредь на эти вопросы отвечать — задавать их тут бесполезно. Для того, чтобы найти ответ на такого сорта вопрос нужно внимательно пошагово прогнать программу и разобраться.
- Если, не смотря на внимательный разбор кода примера, вопрос все равно остался, то задумайтесь, тем ли вы занимаетесь. Математическое моделирование — сфера деятельности, подходящая далеко не всем.
Привет, Вы узнаете про прогнозирование с помощью нейронных сетей, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
прогнозирование с помощью нейронных сетей , настоятельно рекомендую прочитать все из категории Практическое применение методов искусственного интеллекта.
Нейронные сети — это очень мощный и гибкий механизм прогнозирования. При определении того, что нужно прогнозировать, необходимо указывать переменные, которые анализируются и предсказываются. Здесь очень важен требуемый уровень детализации. На используемый уровень детализации влияет множество факторов:
доступность и точность данных, стоимость анализа и предпочтения пользователей результатов прогнозирования. В ситуациях, когда наилучший набор переменных неясен, можно попробовать разные альтернативы и выбрать один из вариантов, дающий наилучшие результаты. Обычно так осуществляется выбор при разработке прогнозирующих систем, основанных на анализе исторических данных.
Второй важный этап при построении нейросетевой прогнозирующей системы — это определение следующих трех параметров: периода прогнозирования, горизонта прогнозирования и интервала прогнозирования.
Общая постановка проблемы. Способности нейронной сети к прогнозированию напрямую следуют из ее способности к обобщению и выделению скрытых зависимостей между входными и выходными данными. После обучения сеть способна предсказать будущее значение некой последовательности на основе нескольких предыдущих значений и/или каких-то существующих в настоящий момент факторов.
Постановка задачи исследования. Необходимо подготовить данные для обучения и проверки корректности работы нейронной сети, выбрать топологию нейронной сети, подобрать ее характеристики и параметры обучения.
Период прогнозирования — это основная единица времени, на которую делается прогноз. Горизонт прогнозирования — это число периодов в будущем, которые покрывает прогноз. То есть, может понадобиться прогноз на 10 дней вперед, с данными на каждый день. В этом случае период — сутки, а горизонт — 10 суток. Наконец, интервал прогнозирования — частота, с которой делается новый прогноз. Часто интервал прогнозирования совпадает с периодом прогнозирования. Выбор периода и горизонта прогнозирования обычно диктуется условиями принятия решений в области, для которой производится прогноз. Выбор этих двух параметров — едва не самое трудное в нейросетевом прогнозировании. Для того чтобы прогнозирование имело смысл, горизонт прогнозирования должен быть не меньше, чем время, необходимое для реализации решения, принятого на основе прогноза. Таким образом, прогнозирование очень сильно зависит от природы принимаемого решения. В некоторых случаях, время, требуемое на реализацию решения, не определено, например, как в случае поставки запасных частей для пополнения запасов ремонтных предприятий. Существуют методы работы в условиях подобной неопределенности, но они повышают вариацию ошибки прогнозирования. Поскольку с увеличением горизонта прогнозирования точность прогноза, обычно, снижается, часто можно улучшить процесс принятия решения, уменьшив время, необходимое на реализацию решения и, следовательно, уменьшив горизонт и ошибку прогнозирования.
В некоторых случаях не так важно предсказание конкретных значений прогнозируемой переменной, как предсказание значительных изменений в ее поведении. Такая задача возникает, например, при предсказании момента, когда текущее направление движения рынка (тренд) изменит свое направление на противоположное.
Точность прогноза, требуемая для конкретной проблемы, оказывает огромное влияние на прогнозирующую систему. Также огромное влияние на прогноз оказывает обучающая выборка.
Первое, с чем сталкивается пользователь любого нейропакета — это необходимость подготовки данных для нейросети. На практике именно предобработка данных может стать наиболее трудоемким элементом нейросетевого анализа. Причем, знание основных принципов и приемов предобработки данных не менее, а может быть даже более важно, чем знание собственно нейросетевых алгоритмов. Последние, как правило, уже «зашиты» в различных нейроэмуляторах, доступных на рынке. Сам же процесс решения прикладных задач, в том числе и подготовка данных, целиком ложится на плечи пользователя.
Рассмотрим задачу прогнозирования объема продаж товаров предприятия. Среда является недетерминированной, так как обычные методы не позволяют со сто процентной уверенностью сказать, что будет в следующий момент времени и выявить все факторы, которые влияют на прогнозируемую величину практически невозможно (можно только ограничить набор факторов). Имеется следующий набор финансовых индикаторов:
Деятельность предприятия:
- история продаж (количество, суммы);
- история состояния склада;
- показатели рекламной активности.
Внешние факторы:
- прайс – листы конкурентов;
- состояние рынка;
- инфляция;
- курсы доллара, евро и т. д.;
- фондовые индексы (РТС, NASDAQ, Dow Jones и другие).
В результате комплексных исследований были выявлены вторичные факторы, оказывающие влияние на объем продаж предприятия, которые необходимо учитывать. Эти показатели представлены в таблице 1 (взята из диссертации Бычкова А.). Как видно из таблицы, перечисленные параметры имеют различную значимость, значения этих параметров имеют разную природу и добываются из различных источников. В результате содержательного анализа перечисленных параметров выявлено, что некоторые из них невозможно включить в модель из-за невозможности получения данных, а отдельные не оказывают сильного влияния на динамику модели и, поэтому их можно без существенной потери точности исключить из модели.
Таблица 1
Вторичные параметры используемые для принятия решений
|
Независимые переменные |
Значимость |
|
1.Концентрация |
++++ |
|
2. Состояние склада |
++++ |
|
3. Экономия от масштаба |
++ |
|
4. Дифференциация продукта |
+++ |
|
5. Интенсивность рекламы |
+++ |
|
6. Отношение активы — объем производства |
++ |
|
7. Рост. |
+++ |
|
8. Диверсификация |
++ |
|
9. Географическое размещение. |
+ |
|
10 . Об этом говорит сайт https://intellect.icu . Риск |
++++ |
|
11. Экспорт |
+ |
|
12. Импорт |
+ |
|
13. Рыночная доля |
+++ |
|
14. Концентрация покупателей |
+ |
|
15. Интенсивность исследований и разработок |
+ |
|
16. Стратегические группировки |
+ |
Следует отметить, что сама история продаж предприятия дает для обучения нейросети примерно 60 % необходимой информации (на основании опыта автора).
Задача прогнозирования объема продаж предприятия обладает теми особенностями, которые делают целесообразным использование нейросетевых методов моделирования и, в частности, топологии «внутренний учитель»:
а) таблица данных может иметь небольшой размер ;
б) в таблице данных могут присутствовать пропуски данных;
в) в данных возможны искажения («шум»);
г) необходима возможность адаптации модели при поступлении новых данных;
д) трудно получить линейную алгебраическую модель;
е) большое количество позиций номенклатуры.
Общий алгоритм прогнозирования с помощью нейронной сети
Алгоритм состоит из следующих пунктов:
- получение временного ряда с интервалом в выбранную временную итерацию;
- заполнение «пробелов» в истории;
- сглаживание ряда методом скользящих средних (или другим);
- получение ряда относительного изменения прогнозируемой величины;
- формирование таблицы «окон» с глубиной погружения временных интервалов;
- добавление к таблице дополнительных данных (например, изменение величины за предыдущие годы);
- шкалирование;
- определение обучающей и валидационной выборок;
- подбор параметров нейросети;
- обучение нейросети;
- проверка работоспособности нейросети в реальных условиях.
Поясним термин «таблицы окон». Данные необходимо преобразовать по специальной схеме. Сначала преобразуем полученный временный ряд в ряд приращений прогнозируемой величины, т. е. будем прогнозировать изменение величины, а не абсолютные значения ряда. Затем выберем глубину погружения, т.е. количество временных интервалов, по которым мы будем прогнозировать следующий. Возьмем глубину погружения равной 4, т.е. прогнозирование величины на следующую итерацию будет осуществляться по результатам четырех предыдущих итераций. Далее следует преобразовать величину к следующему виду:
Таблица 4.1
Первый вариант «окна» данных
|
Hist1 |
Hist2 |
Hist3 |
Hist4 |
Hist0 |
|
D-1 |
D-2 |
D-3 |
D-4 |
D |
|
D-2 |
D-3 |
D-4 |
D-5 |
D-1 |
|
D-3 |
D-4 |
D-5 |
D-6 |
D-2 |
|
… |
… |
… |
… |
… |
Первые четыре колонки являются входами нейросети, последняя – выход, т. е. на основе предыдущих значений изменения величины прогнозируется следующее значение ряда. Таким образом, мы получаем так называемое «скользящее окно», в котором представлены данные за пять недель. Окно можно двигать по временной оси и изменять его ширину. Чтобы учесть предыдущие годы и учесть возможные сезонные зависимости добавим еще один столбец в выборку, который показывает изменение величины в прошлый год за тот же период.
Таблица 4.2
Второй вариант «окна» данных
|
LastY |
Hist1 |
Hist2 |
Hist3 |
Hist4 |
Hist0 |
|
L |
D-1 |
D-2 |
D-3 |
D-4 |
D |
|
L-1 |
D-2 |
D-3 |
D-4 |
D-5 |
D-1 |
|
L-2 |
D-3 |
D-4 |
D-5 |
D-6 |
D-2 |
|
… |
… |
… |
… |
… |
… |
Таким образом, готовится обучающая выборка и именно в таком виде предоставляются данные для последующего анализа. Можно не ограничиваться только прошлым годом, а подавать данные за несколько предыдущих лет, но следует учитывать, что сеть в таком случае разрастается, что иногда приводит к плохим результатам.
К недостаткам прогнозирования с помощью нейронных сетей можно отнести следующее: длительное время обучения, проблема переобучения, трудность определения положения обучающей выборки и значащих входов.
Например, данные по продажам нового товара.
Схему решения задачи прогнозирования можно представить в виде последовательности этапов (рис. 1).
Рис. 1 Схема решения задач прогнозирования
Этап предварительных преобразований. Если временной ряд порождается динамической системой, т.е. значения {a(t)} – произвольная функция состояния такой системы, существует такое число d, что d предыдущих значений временного ряда однозначно определяет следующее значение. На практике большинство прогнозируемых временных рядов порождаются сложными динамическими системами, для которых велико значение d. Кроме того, в самом временном ряде может присутствовать случайная составляющая. Поэтому на данном этапе выполняются предварительные преобразования исходных данных позволяющие уменьшить ошибку прогнозирования.
Рис. 2 Динамика цен на подсолнечник с 2007 по 2010гг
На этапе обучения нейронная сеть восстанавливает целевую функцию по множеству наборов обучающей выборки, т.е. решает задачу интерполяции. На этапе использования обученной нейронной сети (получении прогноза) она будет использовать восстановленную зависимость для получения прогнозируемой величины, т.е. решать задачу экстраполяции. Для корректного решения задачи экстраполяции как задачи интерполяции необходимо обеспечить стационарность временного ряда признаков, распределение значений ряда должно быть инвариантно относительно момента времени, для которого оно построено. Для этого продифференцируем временной ряд: x’i=xi+1-xi (рис. 3).
Рис. 3 Продифференцированный временной ряд
Для улучшения качества и скорости обучения нейронной сети необходимо преобразовать входные данные к диапазону [-1,1]. Формула пересчета значения признака x для i-го примера выборки в интервал [a,b] такова:
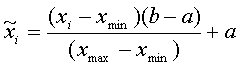
где xmin , xmax — минимальное и максимальное выборочные значения признака.
Из данного множества выделяются два непересекающихся подмножества, хронологически следующих одно за другим. Одно из них представляет собой обучающую выборку, на которой будет выполняться обучение нейронной сети. Другое подмножество представляет собой контрольную выборку, которая не предъявляется нейронной сети в процессе обучения и используется для проверки качества прогноза. Обучающая и контрольная выборки относятся как 2:1.
Этап структурного синтеза нейронной сети. На данном этапе производится выбор архитектуры сети и структура связей между нейронами. В результате исследований в качестве топологии нейронной сети выбран персептрон с 30 входами (x), 80 нейронами скрытого слоя (s) и одним выходным (y).
Рис. 4 Схема нейронной сети
Персептрон представляет собой сеть, состоящую из нескольких последовательно соединенных слоев формальных нейронов МакКаллока и Питтса. На низшем уровне иерархии находится входной слой, состоящий из сенсорных элементов, задачей которого является только прием и распространение по сети входной информации. Далее имеются один или, реже, несколько скрытых слоев. Каждый нейрон на скрытом слое имеет несколько входов, соединенных с выходами нейронов предыдущего слоя или непосредственно со входными сенсорами X1..Xn, и один выход. Нейрон характеризуется уникальным вектором весовых коэффициентов w. Веса всех нейронов слоя формируют матрицу, которую мы будем обозначать W. Функция нейрона состоит в вычислении взвешенной суммы его входов с дальнейшим нелинейным преобразованием ее в выходной сигнал.
Выходы нейронов последнего, выходного, слоя описывают результат классификации Y=Y(X). Особенности работы персептрона состоят в следующем. Каждый нейрон суммирует поступающие к нему сигналы от нейронов предыдущего уровня иерархии с весами, определяемыми состояниями синапсов, и формирует ответный сигнал (переходит в возбужденное состояние), если полученная сумма выше порогового значения. Персептрон переводит входной образ, определяющий степени возбуждения нейронов самого нижнего уровня иерахии, в выходной образ, определяемый нейронами самого верхнего уровня. Число последних, обычно, сравнительно невелико. Состояние возбуждения нейрона на верхнем уровне говорит о принадлежности входного образа к той или иной категории.
Традиционно рассматривается аналоговая логика, при которой допустимые состояния синаптических связей определяются произвольными действительными числами, а степени активности нейронов — действительными числами между 0 и 1. Иногда исследуются также модели с дискретной арифметикой, в которой синапс характеризуется двумя булевыми переменными: активностью (0 или 1) и полярностью (-1 или +1), что соответствует трехзначной логике. Состояния нейронов могут при этом описываться одной булевой переменной. Данный дискретный подход делает конфигурационное пространство состояний нейронной сети конечным (не говоря уже о преимуществах при аппаратной реализации).
Параметрический синтез нейронной сети. В качестве метода обучения нейронной сети будет использоваться алгоритм обратного распространения ошибки. Основная идея обратного распространения состоит в том, как получить оценку ошибки для нейронов скрытых слоев. Заметим, что известные ошибки, делаемые нейронами выходного слоя, возникают вследствие неизвестных пока ошибок нейронов скрытых слоев. Чем больше значение синаптической связи между нейроном скрытого слоя и выходным нейроном, тем сильнее ошибка первого влияет на ошибку второго. Следовательно, оценку ошибки элементов скрытых слоев можно получить, как взвешенную сумму ошибок последующих слоев. При обучении информация распространяется от низших слоев иерархии к высшим, а оценки ошибок, делаемые сетью — в обратном направлении.
На этапе обучения происходит вычисление синаптических коэффициентов w. При этом в отличие от классических методов в основе лежат не аналитические вычисления, а методы обучения по образцам с помощью примеров сгруппированных в обучаемом множестве. Для каждого образа из обучающей выборки считается известным требуемое значение выхода нейронной сети. Этот процесс можно рассматривать как решение оптимизационной задачи. Ее целью является минимизации функции ошибки или невязки Е на обучающем множестве путем выбора значений синоптических коэффициентов w.
В качестве активационной функции нейронов скрытого слоя необходимо взять сигмоидальную функцию, т.к. для возможности применения метода обратного распространения ошибки передаточная функция нейронов должна быть дифференцируема. (2).
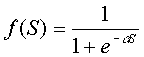
Сигмоид ограничивает диапазон изменения выходного сигнала между нулем и единицей, что повышает устойчивость нейросети. Благодаря нелинейности функции активации нейроны обладают хорошей обучаемостью.
Активационной функцией нейрона выходного слоя выбрана линейная функция (3).
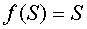
Рис. 5 Проверка обученной нейронной сети
Проверка ошибки прогноза на контрольной выборке. Если значение ошибки находится в допустимых пределах, то задача считается решенной, и обученная нейронная сеть используется для получения прогноза. В данном случае ошибка не превышает 4%.
Опираясь на результаты полученных экспериментальным путем ведущими разработчиками в области нейронных сетей, данная топология нейронной сети и метод ее обучения является одним из оптимальных в задачах прогнозирования.
Выводы.
Нейронные сети — исключительно мощный метод моделирования, позволяющий воспроизводить чрезвычайно сложные зависимости. В статье была доказана возможность и эффективность применения нейронных сетей для прогнозирования временных рядов, рассмотрены топология искусственной нейронной сети, метод ее обучения, входные данные и их предобработка и другие характеристики нейронной сети для прогнозирования финансово-хозяйственных показателей сельскохозяйственного предприятия, выделены основные задачи, которые необходимо выполнить для ее разработки.
К сожалению, в одной статье не просто дать все знания про прогнозирование с помощью нейронных сетей. Но я — старался.
Если ты проявишь интерес к раскрытию подробностей,я обязательно напишу продолжение! Надеюсь, что теперь ты понял что такое прогнозирование с помощью нейронных сетей
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Практическое применение методов искусственного интеллекта
Время на прочтение
11 мин
Количество просмотров 45K
На хабре было множество публикаций по данной теме, но все они говорят о разных вещах. Решил собрать всё в одну кучку и рассказать людям.
Это первая статья серии введения в нейронные сети, «Нейронные сети для начинающих». Здесь и далее мы постараемся разобраться с таким понятием — как нейронные сети, что они вообще из себя представляют и как с ними «подружиться», на практике решая простые задачи.
О чём будем говорить:
- Нейронные сети. Что это такое и какие они бывают?
- Виды нейронных сетей и конструкция нейронных сетей.
- Где они применяются?
- Перцептрон.
- Классификация. Что это такое и почему это важно?
- Функции активации (ФА).
- Зачем они нужны?
- Виды ФА.
- Как обучить нейронную сеть?
- Цели и задачи обучения.
- Обучение с учителем и без.
- Понятие ошибки.
- Задача минимизации ошибки.
- Градиентный спуск.
- Как вычислить градиент?
- Пресловутые «Ирисы Фишера».
- Постановка задачи.
- Softmax()+ Relu()
- Ура! Пишем код (Наконец-то).
Что такое нейронные сети?
Нейро́нная сеть — математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма (в частности, мозга).
▍ Виды нейронных сетей:
Есть десятки видов нейросетей, которые отличаются архитектурой, особенностями функционирования и сферами применения. При этом чаще других встречаются сети трёх видов.
Нейронные сети прямого распространения (Feed forward neural networks, FFNN). Прямолинейный вид нейросетей, при котором соседние узлы слоя не связаны, а передача информации осуществляется напрямую от входного слоя к выходному. FFNN имеют малую функциональность, поэтому часто используются в комбинации с сетями других видов.
Свёрточные нейронные сети (Convolutional neural network, CNN). Состоят из слоёв пяти типов:
- входного,
- свёртывающего,
- объединяющего,
- подключённого,
- выходного.
Каждый слой выполняет определённую задачу: например, обобщает или соединяет данные.
Свёрточные нейросети применяются для классификации изображений, распознавания объектов, прогнозирования, обработки естественного языка и других задач.
Рекуррентные нейронные сети (Recurrent neural network, RNN). Используют направленную последовательность связи между узлами. В RNN результат вычислений на каждом этапе используется в качестве исходных данных для следующего. Благодаря этому, рекуррентные нейронные сети могут обрабатывать серии событий во времени или последовательности для получения результата вычислений.
RNN применяют для языкового моделирования и генерации текстов, машинного перевода, распознавания речи и других задач.
▍ Типы задач, которые решают нейронные сети
Выделяют несколько базовых типов задач, для решения которых могут использоваться нейросети.
- Классификация. Для распознавания лиц, эмоций, типов объектов: например, квадратов, кругов, треугольников. Также для распознавания образов, то есть выбора конкретного объекта из предложенного множества: например, выбор квадрата среди треугольников.
- Регрессия. Для определения возраста по фотографии, составления прогноза биржевых курсов, оценки стоимости имущества и других задач, требующих получения в результате обработки конкретного числа.
- Прогнозирования временных рядов. Для составления долгосрочных прогнозов на основе динамического временного ряда значений. Например, нейросети применяются для предсказания цен, физических явлений, объёма потребления и других показателей. По сути, даже работу автопилота Tesla можно отнести к процессу прогнозирования временных рядов.
- Кластеризация. Для изучения и сортировки большого объёма неразмеченных данных в условиях, когда неизвестно количество классов на выходе, то есть для объединения данных по признакам. Например, кластеризация применяется для выявления классов картинок и сегментации клиентов.
- Генерация. Для автоматизированного создания контента или его трансформации. Генерация с помощью нейросетей применяется для создания уникальных текстов, аудиофайлов, видео, раскрашивания чёрно-белых фильмов и даже изменения окружающей среды на фото.
Как выглядит простая нейронная сеть?
Выяснив, как же она выглядит, мы перед тем, как разобрать её строение: что, зачем и почему — разберёмся, где же они применяются и что с помощью них можно сделать. Вот примерный список областей, где решение такого рода задач имеет практическое значение уже сейчас:
- Экономика и бизнес.
- Медицина и здравоохранение.
- Авионика.
- Связь.
- Интернет.
- Автоматизация производства.
- Политологические и социологические исследования.
- Безопасность, охранные системы.
- Ввод и обработка информации.
- Геологоразведка.
- Компьютерные и настольные игры.
- И т.д.
Теперь разберём подробнее самую простую модель искусственного нейрона — перцептрон:
Согласно общему определению перцептро́н или персептрон — математическая или компьютерная модель восприятия информации мозгом, предложенная Фрэнком Розенблаттом в 1958 году и впервые реализованная в виде электронной машины «Марк-1» в 1960 году. Перцептрон стал одной из первых моделей нейросетей, а «Марк-1» — первым в мире нейрокомпьютером.
Вы уже могли видеть подобные иллюстрации на просторах интернета:
Но что же это всё означает?
Давайте по порядку:
Х1, Х2, Х3, …, Хn — входные классы, данные, которые мы подаём на вход нашей сети. Т.е. здесь у нас идут те данные, которые пришли к нам от клиента или же от нашего сервиса, который каким-то образом собирает/парсит данные , далее эти данные умножаются на случайные веса (стандартное обозначение W1, …, Wn) и суммируются с так называемым нейроном смещения или bias нейрон в «Сумматоре» (из названия следует, что данные, Хn * Wn , суммируются друг с другом). Далее результат Σ(Хn * Wn + b) подаётся в функцию активации, о которой поговорим далее.
Данные метаморфозы проиллюстрированы на следующем слайде:
▍ Задача классификации
Проговорив в общих чертах строение «базовой нейронной сети», плавно перейдём к рассмотрению задачи классификации — основной задачи нейронных сетей.
Итак, из определения следует, что классификация — это задача, при которой по некоторому объекту — исходные данные, нужно предсказать, к какому
классу объектов он принадлежит.
Примитивно эту задачу можно проиллюстрировать следующим образом:
Мы с вами, с лёгкостью можем понять, что ответ будет следующий:
Но а что на это скажет компьютер?
Для него это лишь набор пикселей/байтов, который ему ни о чём не говорит. По-простому — это 0 и 1. Подробнее про это, можете почитать здесь.
Для того, чтобы компьютер понял, что происходит внутри предложенных ему данных, мы должны «объяснить» ему всё и дать какой-то алгоритм, т.е. написать программу.
▍ Функции активации — ФА
Но это будет не просто программа, помимо базового кода, нам необходимо ввести так называемую математическую модель или же функцию активации, что же это такое?
Функция активации определяет выходное значение нейрона в зависимости от результата взвешенной суммы входов и порогового значения. Пример: 𝒚=𝒇(𝒕).
Давайте рассмотрим некоторые распространённые ФА:
Первое, что приходит в голову, это вопрос о том, что считать границей активации для активационной функции. Если значение Y больше некоторого порогового значения, считаем нейрон активированным. В противном случае говорим, что нейрон неактивен. Такая схема должна сработать, но сначала давайте её формализуем.
Функция А = активирована, если Y > граница, иначе нет.
Другой способ: A = 1, если Y > граница, иначе А = 0.
Функция, которую мы только что создали, называется ступенчатой.
Функция принимает значение 1 (активирована), когда Y > 0 (граница), и значение 0 (не активирована) в противном случае.
Пользуясь определением, становится понятно, что ReLu возвращает значение х, если х положительно, и 0 в противном случае.
ReLu нелинейна по своей природе, а комбинация ReLu также нелинейна! (На самом деле, такая функция является хорошим аппроксиматором, так как любая функция может быть аппроксимирована комбинацией ReLu). Это означает, что мы можем стэкать слои. Область допустимых значений ReLu — [ 0,inf ].
ReLu менее требовательно к вычислительным ресурсам, так как производит более простые математические операции. Поэтому имеет смысл использовать ReLu при создании глубоких нейронных сетей.
Сигмоида выглядит гладкой и подобна ступенчатой функции. Рассмотрим её преимущества.
Во-первых, сигмоида — нелинейна по своей природе, а комбинация таких функций производит тоже нелинейную функцию.
Ещё одно достоинство такой функции — она не бинарна, что делает активацию аналоговой, в отличие от ступенчатой функции. Для сигмоиды также характерен гладкий градиент.
Если вы заметили, в диапазоне значений X от -2 до 2 значения Y меняется очень быстро. Это означает, что любое малое изменение значения X в этой области влечёт существенное изменение значения Y. Такое поведение функции указывает на то, что Y имеет тенденцию прижиматься к одному из краёв кривой.
Сигмоида действительно выглядит подходящей функцией для задач классификации. Она стремится привести значения к одной из сторон кривой (например, к верхнему при х=2 и нижнему при х=-2). Такое поведение позволяет находить чёткие границы при предсказании.
Другое преимущество сигмоиды над линейной функцией заключается в следующем. В первом случае имеем фиксированный диапазон значений функции — [0,1], тогда как линейная функция изменяется в пределах (-inf, inf). Такое свойство сигмоиды очень полезно, так как не приводит к ошибкам в случае больших значений активации.
Сегодня сигмоида является одной из самых частых активационных функций в нейросетях.
Как же обучить нейронную сеть?
Теперь перейдём к другим немаловажным терминам.
Что нам понадобится:
- Данные для обучения
- Функция потерь
- Понятие «градиентного спуска»
Цель обучения нейронной сети — найти такие параметры сети, при которых нейронная сеть будет ошибаться наименьшее количество раз.
Ошибка нейронной сети — отличие между предсказанным значением и правильным.
Самая простая функция потерь — Евклидово Расстояние или функция MSE:
yi – правильный результат.
zi – предсказанный результат.
Задача минимизации ошибки:
Используем метод оптимизации:
𝒂𝒓𝒈𝒎𝒊𝒏(𝒕) — функция, возвращающая элемент вектора, где достигается минимум.
𝒂𝒓𝒈𝒎𝒂𝒙(𝒕) — функция, возвращающая элемент вектора, где достигается максимум.
Градиентный спуск — метод нахождения локального минимума или максимума функции при помощи движения вдоль градиента.
Для вычисления градиентного спуска нам надо посчитать частные производные функции ошибки, по всем обучаемым параметрам нашей модели.
Пресловутые «Ирисы Фишера»
Теперь немного уйдём от голой теории и сделаем простую программу, решив базовую задачу классификации. Это базовая задача для специалистов, начинающих свой путь в нейронных сетях, своеобразный «Hello world!», для этого направления.
Здесь хотелось бы сделать небольшое отступление и рассказать подробнее про саму задачу «Ирисов Фишера» зачем и почему она здесь.
Ирисы Фишера — это набор данных для задачи классификации, на примере которого, Рональд Фишер в 1936 году продемонстрировал работу разработанного им метода дискриминантного анализа. Иногда его также называют ирисами Андерсона, так как данные были собраны американским ботаником Эдгаром Андерсоном. Этот набор данных стал уже классическим, и часто используется в литературе для иллюстрации работы различных статистических алгоритмов.
Вот так распределяются данные в датасете:
Ирисы Фишера состоят из данных о 150 экземплярах ириса, по 50 экземпляров из трёх видов:
- Ирис щетинистый (Iris setosa).
- Ирис виргинский (Iris virginica).
- Ирис разноцветный (Iris versicolor).
Для каждого экземпляра измерялись четыре характеристики (в сантиметрах):
- Длина чашелистника (sepal length).
- Ширина чашелистника (sepal width).
- Длина лепестка (petal length).
- Ширина лепестка (petal width).
Конструкция нейронной сети:
На входе у нас есть 4 класса(характеристики) — Х, также нам понадобится всего один внутренний слой — Н, в нём будет 10 нейронов (выбирается методом подбора), далее на выходе мы имеем 3 класса, которые зависят от характеристики цветов — Z. Получается вот такая конструкция сети:
Далее распишем математическое обоснование для нашей задачи:
Ура-а-а-а! Наконец-то код!
Нам потребуется:
- Язык программирования Python.
- Базовая библиотека языка Python, для работы с линейными данными, NumPy.
- Базовая библиотека языка Python, для «рандомизации» значений, random.
Для начала нам необходимо импортировать библиотеки numpy и random:
import numpy as np
import random as rdТеперь пропишем некоторые гиперпараметры:
INPUT_DIM = 4 #кол-во входных нейронов
OUT_PUT = 3 #кол-во выходных нейронов
H_DIM = 10 #кол-во нейронов в скрытом слое
Теперь зададим входной вектор и его веса (вначале рандомим данные, для получения реальной картины весов):
x = np.random.randn(INPUT_DIM)
w1 = np.random.randn(INPUT_DIM, H_DIM)
b1 = np.random.randn(H_DIM)
w2 = np.random.randn(H_DIM, OUT_DIM)
b2 = np.random.randn(OUT_DIM)
Расписываем вложенный слой — наше математическое обоснование:
t1 = x @ w1 + b1
h1 = relu(t1)Точно также сделаем и для остальных.
Теперь обернём наш код в функцию:
def predict(x):
t1 = x @ W1 + b1
h1 = relu(t1)
t2 = h1 @ W2 + b2
z = softmax(t2)
print('z =', z)
return z
Оформим функцию relu():
def relu(t):
print('relu:', np.maximum(t, 0))
return np.maximum(t, 0)
Теперь добавим softmax():
def softmax(t):
out = np.exp(t)
print('softmax:', out / np.sum(out))
return out / np.sum(out)
Добавим вызов функции predict(), также class_names — имена выходных классов и вывод результатов предсказания:
probs = predict(x)
pred_class = np.argmax(probs)
class_names = ['Setosa', 'Versicolor', 'Virginica']
print('Predicted:', class_names[pred_class])
Наш код здесь нарандомит значения входных коэффициентов и весов, поэтому и результат будет случайный. Для тех, кто хочет весь код сразу:
import numpy as np
import random as rd
INPUT_DIM = 4
OUT_DIM = 3
H_DIM = 10
x = []
for i in range(4):
x.append(float(input()))
print(x)
# Рандомно вводим значения гиперпараметров:
x = np.random.randn(INPUT_DIM)
w1 = np.random.randn(INPUT_DIM, H_DIM)
b1 = np.random.randn(H_DIM)
w2 = np.random.randn(H_DIM, OUT_DIM)
b2 = np.random.randn(OUT_DIM)
def relu(t):
print('relu:1', np.maximum(t, 0))
return np.maximum(t, 0)
def softmax(t):
out = np.exp(t)
print('softmax:', out / np.sum(out))
return out / np.sum(out)
def predict(x):
t1 = x @ w1 + b1
h1 = relu(t1)
t2 = h1 @ w2 + b2
z = softmax(t2)
print('z =1', z)
return z
tl = x @ w1 + b1
hl = relu(tl)
probs = predict(x)
pred_class = np.argmax(probs)
class_names = ['Setosa', 'Versicolor', 'Virginica']
print('Predicted:', class_names[pred_class])Вот теперь добавим полученные после обучения веса и входные данные:
w1 = np.array([[ 0.33462099, 0.10068401, 0.20557238, -0.19043767, 0.40249301, -0.00925352, 0.00628916, 0.74784975, 0.25069956, -0.09290041 ], [ 0.41689589, 0.93211640, -0.32300143, -0.13845456, 0.58598293, -0.29140373, -0.28473491, 0.48021000, -0.32318306, -0.34146461 ], [-0.21927019, -0.76135162, -0.11721704, 0.92123373, 0.19501658, 0.00904006, 1.03040632, -0.66867859, -0.01571104, -0.08372566 ], [-0.67791724, 0.07044558, -0.40981071, 0.62098450, -0.33009159, -0.47352435, 0.09687051, -0.68724299, 0.43823402, -0.26574543 ]])
b1 = np.array([-0.34133575, -0.24401602, -0.06262318, -0.30410971, -0.37097632, 0.02670964, -0.51851308, 0.54665141, 0.20777536, -0.29905165 ])
w2 = np.array([[ 0.41186367, 0.15406952, -0.47391773 ], [ 0.79701137, -0.64672799, -0.06339983 ], [-0.20137522, -0.07088810, 0.00212071 ], [-0.58743081, -0.17363843, 0.93769169 ], [ 0.33262125, 0.18999841, -0.14977653 ], [ 0.04450406, 0.26168097, 0.10104333 ], [-0.74384144, 0.33092591, 0.65464737 ], [ 0.45764631, 0.48877246, -1.16928700 ], [-0.16020630, -0.12369116, 0.14171301 ], [ 0.26099978, 0.12834471, 0.20866959 ]])
b2 = np.array([-0.16286677, 0.06680119, -0.03563594 ])
Опять же для любителей всего кода в одном месте:
import numpy as np
import random as rd
INPUT_DIM = 4
OUT_DIM = 3
H_DIM = 10
x = []
# Входные тестовые данные вводятся в следующем формате: "7.9 3.1 7.5 1.8"
# Длина чашелистника: 7.9
# Ширина чашелистника: 3.1
# Длина лепестка: 7.5
# Ширина лепестка: 1.8
for i in range(4):
x.append(float(input()))
print(x)
w1 = np.array([[ 0.33462099, 0.10068401, 0.20557238, -0.19043767, 0.40249301, -0.00925352, 0.00628916, 0.74784975, 0.25069956, -0.09290041 ], [ 0.41689589, 0.93211640, -0.32300143, -0.13845456, 0.58598293, -0.29140373, -0.28473491, 0.48021000, -0.32318306, -0.34146461 ], [-0.21927019, -0.76135162, -0.11721704, 0.92123373, 0.19501658, 0.00904006, 1.03040632, -0.66867859, -0.01571104, -0.08372566 ], [-0.67791724, 0.07044558, -0.40981071, 0.62098450, -0.33009159, -0.47352435, 0.09687051, -0.68724299, 0.43823402, -0.26574543 ]])
b1 = np.array([-0.34133575, -0.24401602, -0.06262318, -0.30410971, -0.37097632, 0.02670964, -0.51851308, 0.54665141, 0.20777536, -0.29905165 ])
w2 = np.array([[ 0.41186367, 0.15406952, -0.47391773 ], [ 0.79701137, -0.64672799, -0.06339983 ], [-0.20137522, -0.07088810, 0.00212071 ], [-0.58743081, -0.17363843, 0.93769169 ], [ 0.33262125, 0.18999841, -0.14977653 ], [ 0.04450406, 0.26168097, 0.10104333 ], [-0.74384144, 0.33092591, 0.65464737 ], [ 0.45764631, 0.48877246, -1.16928700 ], [-0.16020630, -0.12369116, 0.14171301 ], [ 0.26099978, 0.12834471, 0.20866959 ]])
b2 = np.array([-0.16286677, 0.06680119, -0.03563594 ])
# x = np.random.randn(INPUT_DIM)
# w1 = np.random.randn(INPUT_DIM, H_DIM)
# b1 = np.random.randn(H_DIM)
# w2 = np.random.randn(H_DIM, OUT_DIM)
# b2 = np.random.randn(OUT_DIM)
def relu(t):
print('relu:1', np.maximum(t, 0))
return np.maximum(t, 0)
def softmax(t):
out = np.exp(t)
print('softmax:', out / np.sum(out))
return out / np.sum(out)
def predict(x):
t1 = x @ w1 + b1
h1 = relu(t1)
t2 = h1 @ w2 + b2
z = softmax(t2)
print('z =1', z)
return z
tl = x @ w1 + b1
hl = relu(tl)
probs = predict(x)
pred_class = np.argmax(probs)
class_names = ['Setosa', 'Versicolor', 'Virginica']
print('Predicted:', class_names[pred_class])И в итоге мы получим нужное нам предсказание
Полноценный код можно также посмотреть в моём github-репозитории по ссылке.
Ну что же, мы с вами написали свой «Hello world» с нейронными сетями! Эта задача показывает одно из самых популярных направлений в DataSciense — направление классификации данных. Этим мы приоткрыли дверь в большой и быстроразвивающийся мир человекоподобных технологий. Дальше больше!
А какие примеры классификации и интересные задачи из направления DataSciense вы знаете? Пишите свой вариант в комментариях!
Оглавление:
- Что такое искусственные нейронные сети?
- Виды обучения нейронных сетей
- Многослойные нейронные сети и их базовые понятия
- Разбираемся на примере
- Заключение
Что такое искусственные нейронные сети?
Данная статья предназначена для ознакомления читателя с искусственными нейронными сетями (далее ANN – Artificial Neural Network) и базовыми понятиями многослойных нейронных сетей.
Основным элементом ANN является нейрон. Его основной задачей является перемножение предыдущих значений нейронов или входных значений с соответствующими им весовыми коэффициентами связей между соответствующими нейронами, после активации вычисленного значения.
Основными задачами ANN является классификация, принятие решения, анализ данных, прогнозирование, оптимизация.
Искусственные нейронные сети категорируются по топологии (полносвязные, многослойные, слабосвязные), способу обучения (с учителем, без учителя, с подкреплением), модели нейронной сети (прямого распространения, рекррентные нейронные сети, сверточные нейронные сети, радиально-базисные функции), а также по типу связей (полносвязные, многослойные, слабосвязные). Такой значительно большой тип категорирования связан с разнообразием задач, которые ставятся перед ANN. Примеры, приведенные в скобках являются одними из самых распространенных типов категорирования, на самом деле их значительно больше.
Виды обучения нейронных сетей
Обучение с учителем
Данный тип обучения является самым простым, за счет того, что нет необходимости в написании алгоритмов самообучения. Для обучения с учителем требуется размеченный и структурированный набор данных для обучения. Под словом «размеченный» подразумевается процесс обозначения верного ответа на конкретный набор входных данных, который мы ожидаем от нейронной сети как результат работы. За счет таких данных нейронная сеть будет ориентироваться на разметку и корректировать процесс обучения за счет определения совершенных ошибок, которые будут определяться из данных разметки и ее предсказанных данных.
Обучение без учителя
Под обучением без учителя подразумевается процесс обучения нейронной сети без какого-либо контроля с нашей стороны. Весь процесс будет протекать за счет нахождения нейронной сетью корреляции в данных, извлечения полезных признаков и их анализа.
Существуют несколько способов обучения без учителя: обнаружение аномалий, ассоциации, автоэнкодеры и кластеризация.
На основе алгоритмов, описанных выше, в процессе обучения будет определяться значение ошибки, допущенной на каждом шаге обучения, за счет чего будет происходить корректировка обучения, следовательно, нейронная сеть обучится. За счет наличия алгоритмов, процесс написания которых занимает много времени и сильно усложняет моделирование нейронной сети, данный тип обучения считается самым сложным.
Обучение с подкреплением
Обучение с подкреплением или частичным вмешательством учителя можно считать золотой серединой в обучении нейронных сетей. Данный тип обучения представляет собой обучение без учителя с периодической его корректировкой. Корректировка обучения происходит тогда, когда нейронная сеть допускает ошибки при обучении.
Многослойные нейронные сети и их базовые понятия
Каждая ANN имеет входной, выходной и скрытые слои. Количество скрытых слоев и их сложность (количество искусственных нейронов) зачастую играют важную роль в процессе обучения, обеспечивая хорошее обучение модели нейронной сети.
Многослойными ANN называются нейронные сети, у которых количество скрытых слоев более одного. Пример многослойной нейронной сети:
Входной, выходной и скрытые слои, нормализация и зачем все это нужно?
Входной слой дает возможность «скормить» данные, на которых требуется производить обучение. Выходной, в свою очередь, выдает результат работы нейронной сети. Вся суть заключается в скрытых слоях. Повторюсь, количество скрытых слоев и их сложность определяют качество обучения. Объясню на простом примере. Я, при написании модели нейронной сети, которая классифицирует рукописные цифры, смоделировал нейронную сеть из двух скрытых слоев по 30 нейронов в каждом. На вход подавал изображение 28х28 пикселей, но предварительно проведя нормализацию (объясню чуть ниже) входных значений и приведение изображения к виду 784х1, путем расставления всех столбцов в один. Т.е. входными значениями являлись 0 и 1, а если быть точнее — значения из данного диапазона. Так вот эти 0 и 1 оказались на входном слое, т.е. каждый нейрон входного слоя представлял из себя пиксель исходного изображения. Далее следовал скрытый слой, состоящий из 30 нейронов. Так вот, эти 30 нейронов представляют собой 30 участков исходного изображения, а каждый участок в свою очередь содержит какие-либо признаки, характеризующие изображение как определенную цифру. Т.е. чем больше нейронов в скрытых слоях, тем точнее будет представление и градуировка исходного изображения. Будет «плодиться» больше характеристик, по которым нейронная сеть будет классифицировать изображение должным образом.
Вернусь к такому понятию, как нормализация. Она необходима для приведения входных значений к значениям из диапазона 0 и 1. Смысл заключается в том, что нейронная сеть должна явно или с долей вероятности классифицировать изображение, или дать какое-то предсказание. Раз предсказание представляет собой вероятность, то и входные значения должны быть в диапазоне от 0 до 1. Поэтому нормализация, к примеру, значений пикселей изображения, происходит путем деления на 255, т.к. значения пикселей находятся в диапазоне от 0 до 255 и максимальным значением является значение 255.
Весовые коэффициенты
Каждая связь между искусственными нейронами обладает весовым коэффициентом, который постоянно изменяется в процессе обучения и является величиной, которая увеличивает или уменьшает предсказанную вероятность. К примеру, при уменьшении веса связи между 1 и 2 нейроном и увеличении веса между 1 и 3 получим, что, используя сигмоидальную функцию активации, значение на ее выходе в 1-ом случае будет стремиться к 0, а во втором к 1. Т.е. весовые коэффициенты являются своего рода возбудителями искусственных нейронов к прогнозированию.
Функция активация, виды и особенности
Функция активации является нормализующим звеном на каждом слое нейронной сети. Она представляет из себя функцию, которая приводит входное значение к значению от 0 до 1. Одной из самых распространенных функция активации является сигмоидальная функция активации:
Значение ‘х’ является значением, которое обрабатывается функцией активации. Оно включает в себя алгебраическую сумму произведений значений нейронов на предыдущем слое на соответствующие им связи с тем нейроном, на котором мы производим расчет функции активации, а также нейрон смещения.
Пример вычисления функции активации приведен на рис. 5
Распространенные виды функций активации:
- Активация пороговой функции; функция активирована, если x, не активирована, если х<0
- Гиперболическая касательная функция ошибки; функция нелинейна, ее значения находятся в диапазоне (-1;1)
- ReLu и LeakyReLu; функция ReLu равна при х, при x, а при х<0 равна 0. Отличием LeakyReLu от ReLu является наличие коэффициента, определяющего значение функции при х<0 как ах
Функция ошибки, виды
Функция ошибки необходима для определения ошибки прогнозирования, допускаемой нейронной сетью на каждом этапе обучения и корректировкой процесса обучения, за счет корректировки весовых значений связей между искусственными нейронами.
Примеры функций ошибок:
- Кросс-энтропия
- Квадратичная (среднеквадратичное отклонение)
- Расстояние Кульбака — Лейблера
- Экспоненциальная
Самая простая и часто используемая функция ошибок (функция потерь) – среднеквадратичное отклонение.
Она вычисляется как половина от алгебраической суммы квадрата разности, прогнозируемого нейронной сетью значения и реальным значением – разметкой данных.
Backpropagation или обратное распространение ошибки
Для корректировки весов на каждом слое нейронной сети необходима метрика для определения ошибки каждого веса, с этой целью был разработан алгоритм обратного распространения ошибки. Он работает следующим образом:
- Вычисляется прогнозируемое нейронной сетью значение на выходе ANN
- Производится расчет функции ошибки, к примеру, среднеквадратичной
- Корректируются веса связей нейронов на последнем слое на основе вычисленной ошибки на выходе
- Происходит расчет ошибки на предпоследнем слое нейронной сети на основании скорректированных весов связей на последнем слое и ошибки на выходе ANN
- Процесс повторяется до первого слоя нейронной сети
Пример работы алгоритма обратного распространения ошибки:
Bias или нейрон смещения
Значение смещения позволяет сместить функцию активации влево или вправо, что может иметь решающее значение для успешного обучения, а также позволяет быть более гибким при выборе решения или прогнозировании.
При наличии нейрона смещения, его значение тоже поступает на вход функции активации, складываясь с алгебраической суммой произведений нейронов и их весовых коэффициентов.
Пример работы нейрона смещения:
Разбираемся на примере
В данном примере напишем классификатор рукописных цифр на языке программирования С++. Обучающую выборку найдем на официальном сайте MNIST.
В первую очередь импортируем модули:
Определим обучающую выборку ‘dataset’, и загрузим в нее размеченные изображения MNIST.
Создадим входной слой равный 784 нейронам, так как наши изображения равны 28х28 пикселей и мы разложим их в цепочку пикселей 784х1, чтобы подать на вход нейронной сети; два скрытых слоя размера 30 нейронов каждый (размеры скрытых слоев подбирались случайно); выходной слой размером 10 нейронов, так как наша нейросеть будет классифицировать числа в диапазоне 0-9, где первый нейрон будет отвечать за классификацию числа 0, второй за число 1 и так далее до 9.
Необходимо сразу инициализировать наши значения слоев, к примеру 0.
Создадим матрицы весов между входным и 1-м скрытым слоями, 1-м скрытым и 2-м скрытым слоями, 2-м скрытым и выходным слоями, и инициализируем матрицы случайными значениями, как показано на рисунке. На примере значения весов находятся в диапазоне [-1;1].
Также необходимо создать массивы, которые будут содержать в себе значения алгебраической суммы произведения весов на соответствующие нейроны, как было описано выше в статье, после чего эти значения будут подаваться в функцию активации.
Ниже были созданы массивы ошибок на каждом слое. Для сохранения результатов ошибок на каждом нейроне, были инициализированы количество эпох и скорость обучения (определяет скорость перемещения по функции в поисках минимума во время обучения; необходимо быть осторожным с этим значением, так как если оно будет слишком мало, то, есть вероятность остаться в локальном минимуме, не найдя настоящий минимум функции или наоборот, при слишком большом значении, есть вероятность перескочить главный минимум функции.)
На данном этапе начинается процесс обучения нашей нейронной сети. Внешний цикл определяет количество эпох обучения, а внутренний количество итераций обучения в каждой эпохе.
На рисунке ниже инициализируются значения из обучающей выборки MNIST и занесения их на входной слой нейронной сети, а после происходит инициализация S-величин, о которых было сказано выше, нулями
Ниже происходит подсчет алгебраической суммы значений произведений веса на соответствующий нейрон, а после прохождение их через функцию активации, где в роли функции активации выступает сигмоидальная функция.
Подсчитав значения на каждом слое, происходит инициализация массивов ошибок, путем заполнения их 0, а также определение ошибок на выходном слое, путем вычитания полученных значений из 1, и последующим умножением на произведение значений нейронов прошедших через функцию активации на выходном слое на разницу между 1 и этими же значениями.
Далее необходимо определить ошибки на каждом слое нейронной сети методом обратного распространения ошибки. К примеру, чтобы найти ошибку на первом нейроне предыдущего слоя от выходного слоя, необходимо найти алгебраическую сумму произведения ошибок нейронов на выходном слое на соответствующие им веса связей с первым нейроном предыдущего слоя и перемножить на произведение значения нейронов на предпоследнем слое на разницу 1 и этих же значений. Таким образом необходимо найти допущенные ошибки нейронной сетью на каждом слое.
После определения ошибок, допущенных нейронной сетью на каждом нейроне, приступаем к корректировке весовых коэффициентов связей между каждым нейроном. Алгоритм корректировки представлен ниже.
Скорректировав веса, определяем максимальное полученное значение на выходном слое, тем самым определим ответ нейронной сети после прохождения через нее изображения.
Заключение
В этой статье мы разобрались с базовыми понятиями искусственных нейронных сетей, а именно с такими как: входной, выходной, скрытые слои и их предназначение, весовыми коэффициентами связи между искусственными нейронами, функцией активации и ее предназначением, методами определения ошибки на каждом искусственном, с понятием нейрона смещения и функциями ошибки. В следующей статье мы перейдем к изучению нового класса нейронных сетей, таких как сверточные нейронные сети (CNN).
Желаю всем успехов в изучении!
Библиографическое описание:
Кулбараков, М. А. К задаче прогнозирования энергопотребления с помощью нейронных сетей / М. А. Кулбараков. — Текст : непосредственный // Молодой ученый. — 2014. — № 11 (70). — С. 22-25. — URL: https://moluch.ru/archive/70/12122/ (дата обращения: 06.06.2023).
Ключевые слова: нейронные сети, прогнозирование, моделирование, энергопотребление
Введение. В настоящее время на предприятиях осуществляется контроль различных показателей электрическими средствами, с помощью химического или физического анализа и т. д. От способа измерения зависит дискретность контроля и своевременность получения значений. В случае прогнозирования энергопотребления необходимо иметь данные о таких характеристиках как температура и потребляемая мощность за один час. Рассматриваемые характеристики измеряются электрическими средствами, т. е. дискретность контроля мала, и результаты можно использовать незамедлительно. Однако стоит задача обработки большого количества информации. В данной работе предлагается использовать нейронные сети для получения значения энергопотребления, обучение которой происходит по методу обратного распространения ошибки. Также проведено сравнение рассматриваемого метода с встроенным методом для построения нейронной сети программного пакета Matlab.
Обучение нейронной сети по методу обратного распространения ошибки. Основная идея этого метода состоит в распространении сигналов ошибки от выходов сети к её входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Для возможности применения метода обратного распространения ошибки передаточная функция нейронов должна быть дифференцируема. Метод является модификацией классического метода градиентного спуска.
Прогнозирование с помощью нейронной сети методом обратного распространения ошибки происходило в несколько этапов:
Этап 1. Инициализация и исходные данные. Исходные данные по энергопотреблению имеют значения за период с 01.01.2010 по 31.03.2011. Обучение сети, то есть определение весов и смещений для всех нейронов выполняется на периоде значений с 01.01.2010 по 31.12.2010. В качестве тестового был выбран период с 01.01.2011 по 31.03.2011.
Этап 2. Предварительная обработка исходных данных. Нейронная сеть работает со значениями временных рядов от 0 до 1. Исходные значения энергопотребления в массиве выходят далеко за этот диапазон. Для использования нейронной сети необходимо предварительно нормировать исходный временной ряд, как показано на рис. 1.
Рис. 1. График нормированных значений энергопотребления
Этап 3. Настройка нейронной сети. Для прогнозирования использовалась трехслойная полносвязная нейронная сеть (рис. 2).
Рис.2. Структура нейронной сети
В результате эксперимента было выявлено, что наилучший результат получается, если на вход нейронной сети подается 24 значения за двое предыдущих суток, скрытый слой после нескольких попыток стал содержать 72 нейрона, а на выходе мы получаем 24 спрогнозированных значений энергопотребления на будущие сутки (рис. 3).
Этап 4. Обучение сети. Двойной цикл по эпохам и внутренней корректировки был взят из примера Хайкина [1]. Такое обучение называется обучением нейронной сети по методу “back propagation error” (обратное распространение ошибки).
Этап 5. Тестовое прогнозирование. На пятом этапе формируется тестовый массив и прогнозируются значения энергопотребления с помощью полученной нейронной сети (рис. 3). При подаче на вход нейронной сети 48 значений энергопотребления график модели и объекта имеют вид, представленный на рис. 3.
Рис. 3. График фактического и спрогнозированного значения
Количество эпох обучения 600. О качестве полученной модели будем судить по значению средней абсолютной ошибке в процентах (MAPE).
Ошибка прогнозирования MAPE в данном случае получилась равной 13.725 %. Судя по величине ошибки модель адекватно описывает поведение объекта.
На рис. 4 представлен график модели и объекта, при подаче на вход нейронной сети 24 значения энергопотребления, т. е. при прогнозе учитываем предыдущие сутки.
Рис. 4. График фактического и спрогнозированного значения
Количество эпох обучения 600. Величина MAPE оставила около 10.8845 %, что показывает в целом адекватность разработанной нейросетевой модели прогнозирования. Созданная нейронная сеть обучается очень быстро: от 60 до 120 секунд в зависимости от мощности компьютера.
Использование встроенного функционала Matlab для построения нейронной сети. Для реализации нейронно-сетевых концепций разработано большое количество специализированных программных средств. Пакет фирмы «The MathWorks» MATLAB также предоставляет пользователям возможность работы с нейронными сетями. Использование «Neural Network Toolbox» совместно с другими средствами MATLAB открывает широкий простор для эффективного комплексного использования современных математических методов для решения самых разных задач прикладного и научного характера.
Для построения модели прогнозирования энергопотребления был доработан типовой функционал среды Matlab. Обучение сети происходило с помощью алгоритма Левенберга — Маркуардта. Обучающая выборка составляла 80 % от всего объема выборки. Тестовая выборка 20 %. Полный объем выборки равен 10320 значениям энергопотребления на каждый час.
На рис. 5 изображен график прогнозирования энергопотребления методом нелинейной авторегрессии (NAR).
Рис. 5. График модели и объекта
В этом случае на вход подавались значения только энергопотребления. Для прогноза следующего значения энергопотребления использовались ранее спрогнозированные значения.
Величина MAPE составила 3.32652 %, что показывает адекватность разработанной нейросетевой модели прогнозирования. Однако это далеко не предел точности. Предлагается при обучении сети использовать метод нелинейной авторегрессии с расширенным входом. Помимо энергопотребления на вход также подается температура.
Ошибка прогнозирования MAPE, с использованием метода нелинейной авторегрессии с расширенным входом, составила всего 2.46294 %. При таких небольших значениях ошибки разница с предыдущим методом обучения нейронной сети весьма ощутима. При прогнозировании энергопотребления борьба за десятые доли процентов ведется постоянно, так как, например, расходы на покупку электроэнергии напрямую зависят от точности прогноза собственного энергопотребления.
Заключение. Прогнозирование временных рядов энергопотребления показало высокую эффективность реализованных моделей. Значения ошибки прогнозирования MAPE при обучении сети методом обратного распространения ошибки лежит в пределах от 10.8 % до 13 %, что сравнительно хуже значений, полученных при помощи новейших методов обучения нейронной сети.
Литература:
1. Хайкин, С. Нейронные сети: полный курс / С. Хайкин. — М.: ООО «И. Д. Вильямс», 2008. — 1104 с.
Основные термины (генерируются автоматически): нейронная сеть, MAPE, обратное распространение ошибки, MATLAB, значение энергопотребления, обучение сети, нелинейная авторегрессия, NAR, график модели, дискретность контроля.




 при прогнозировании на нейронных
при прогнозировании на нейронных




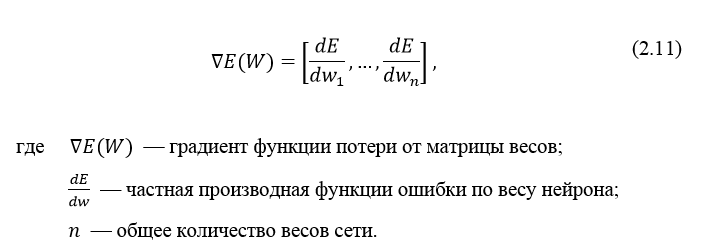


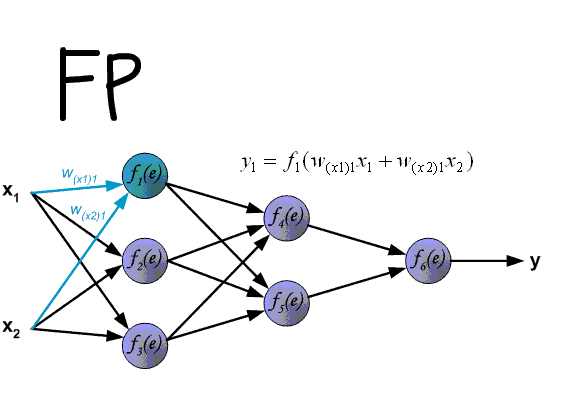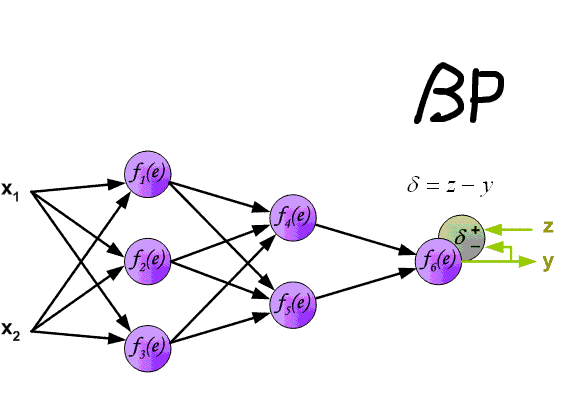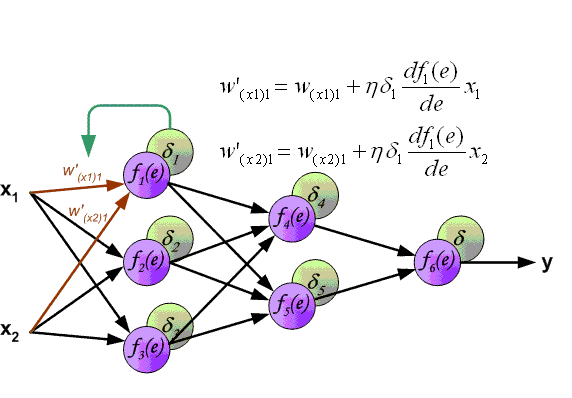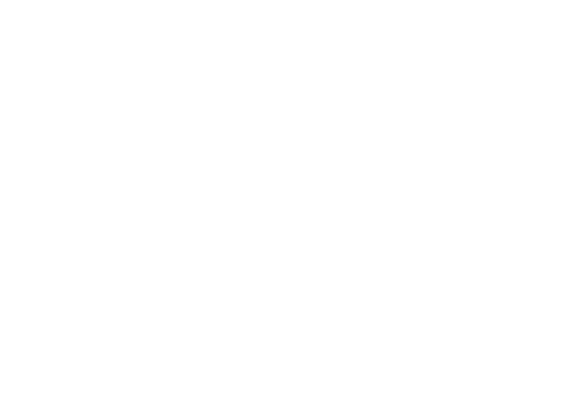
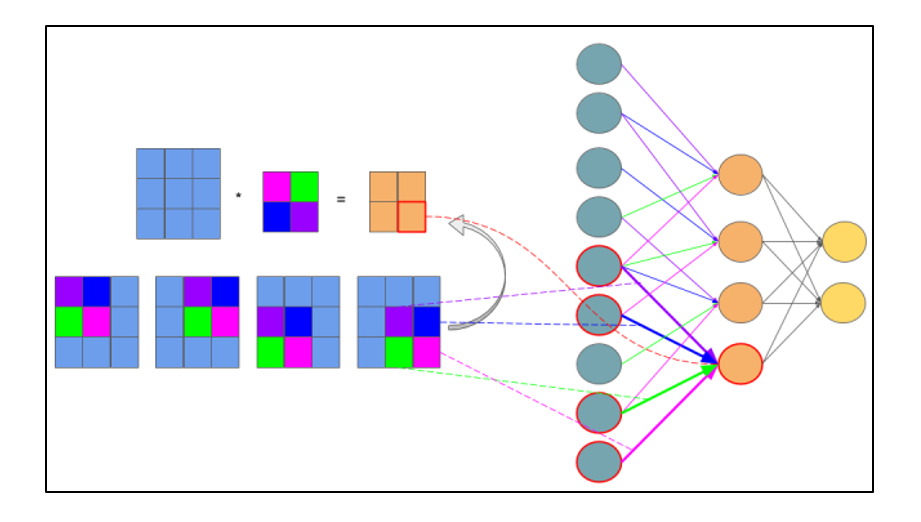
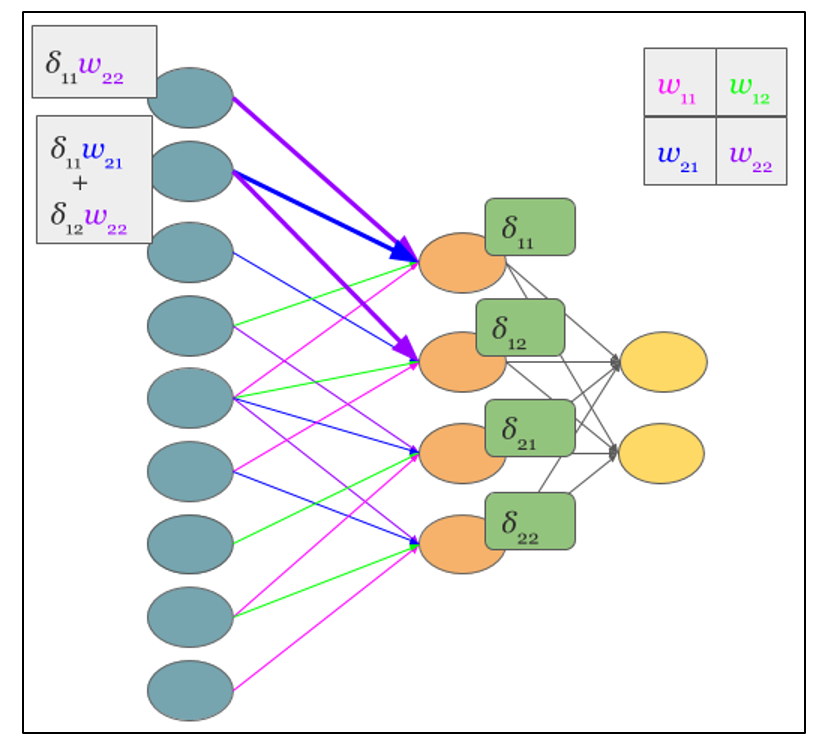

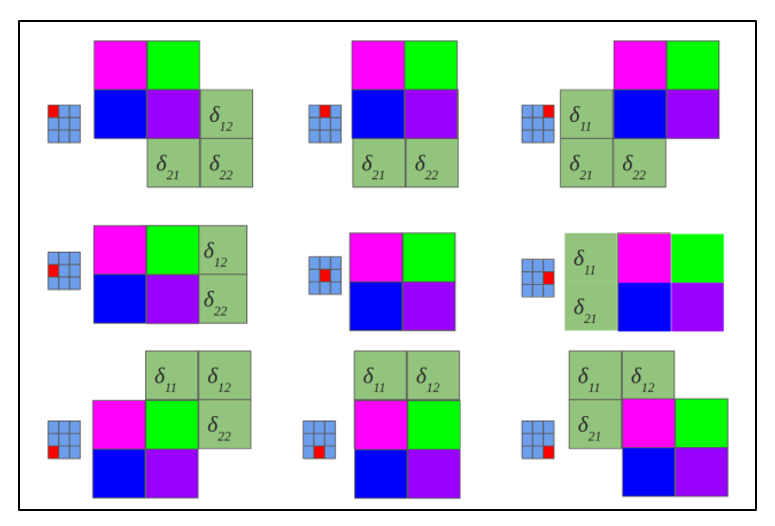



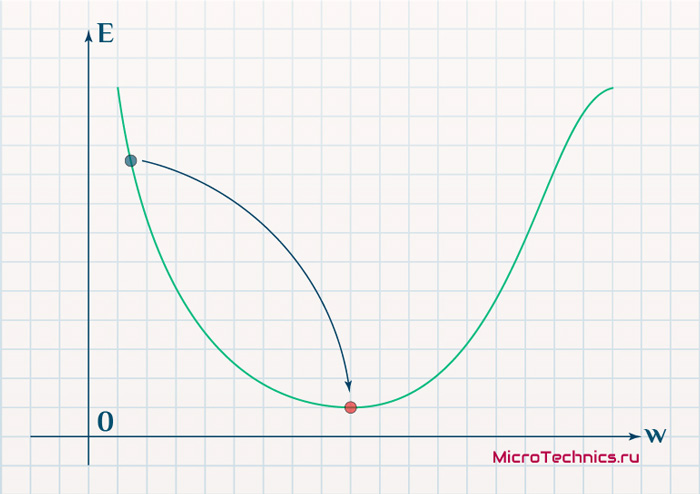
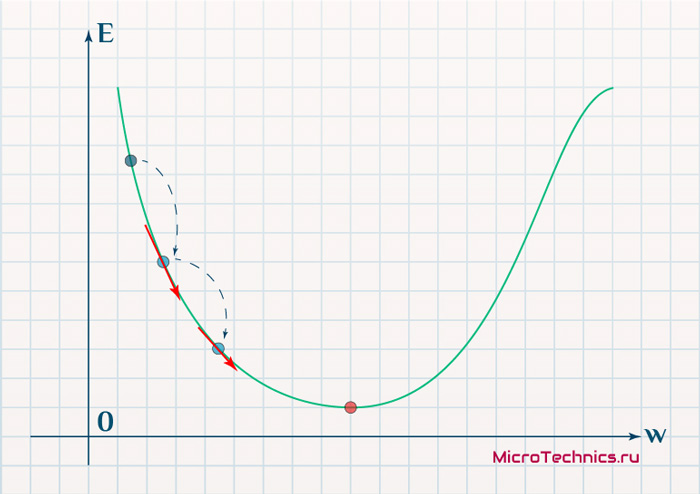
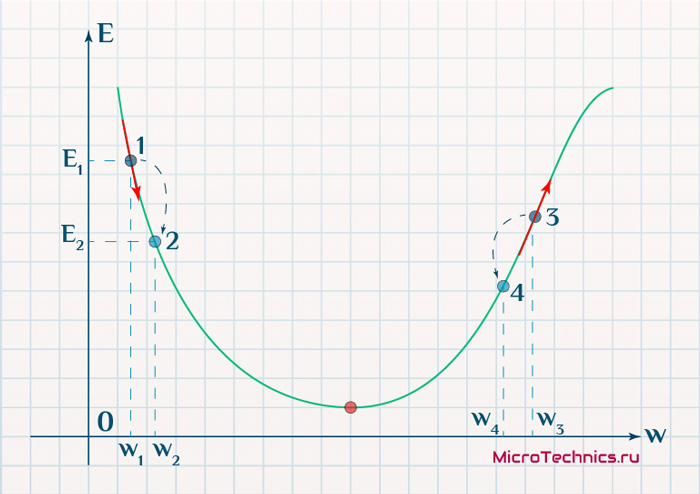
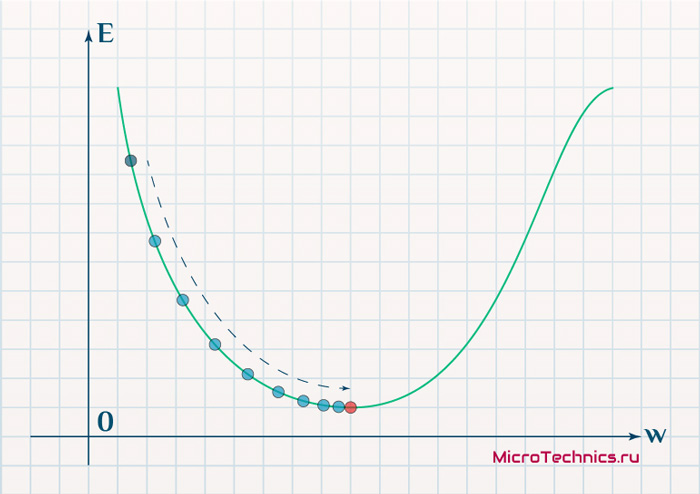
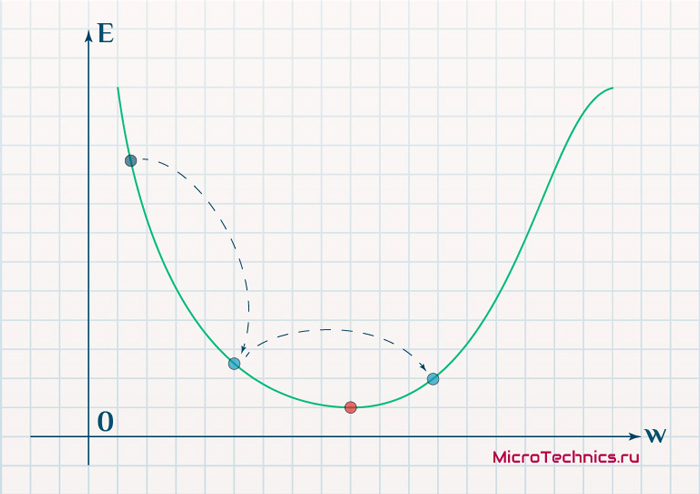
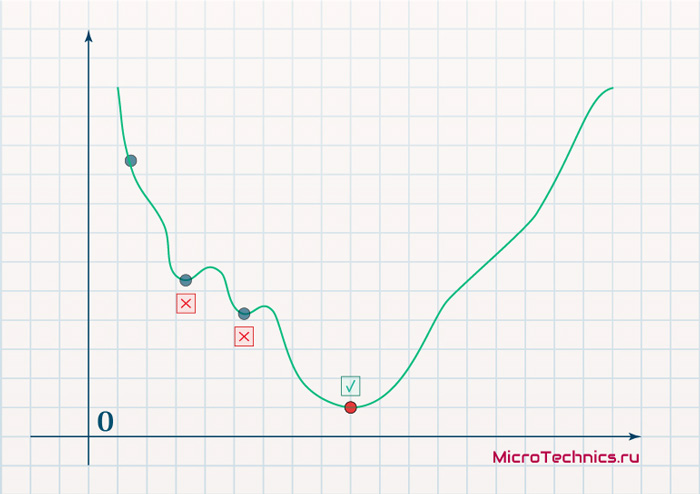
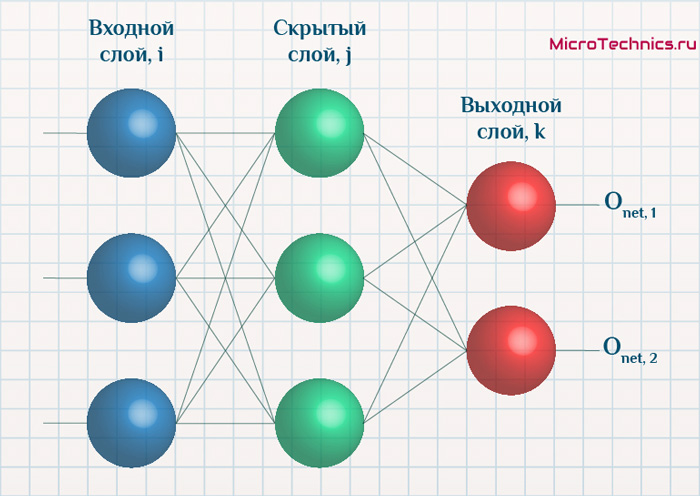
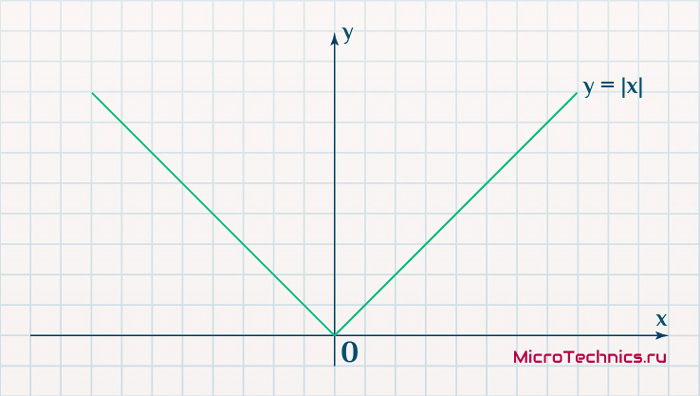
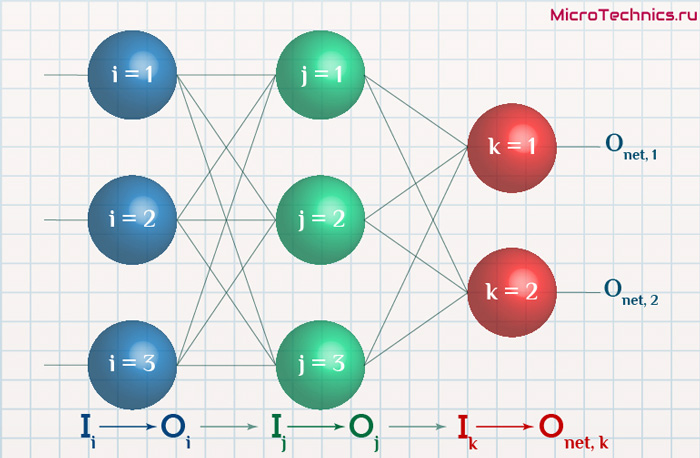
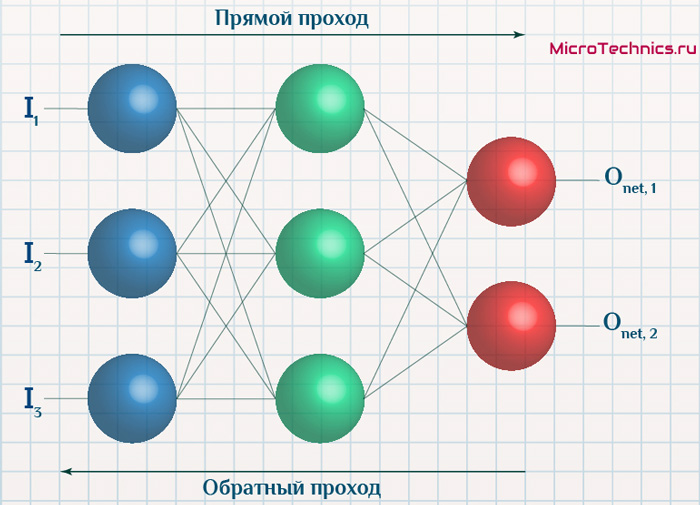
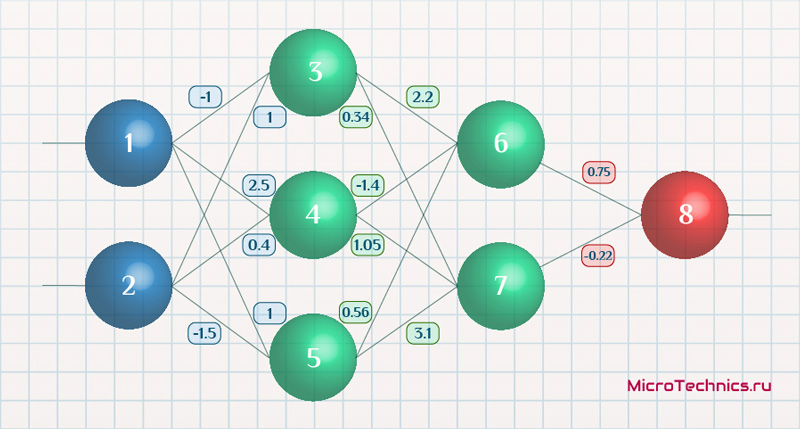
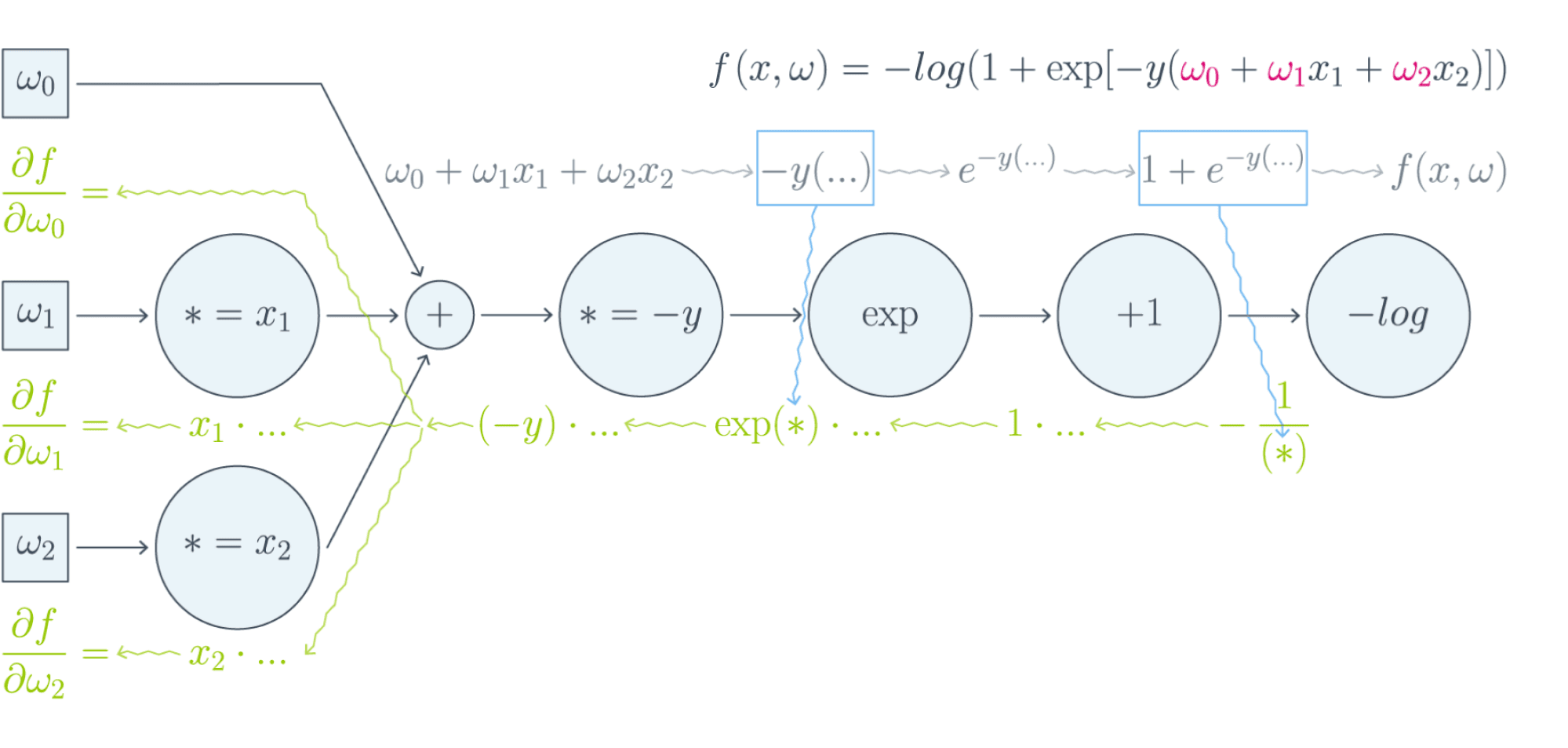
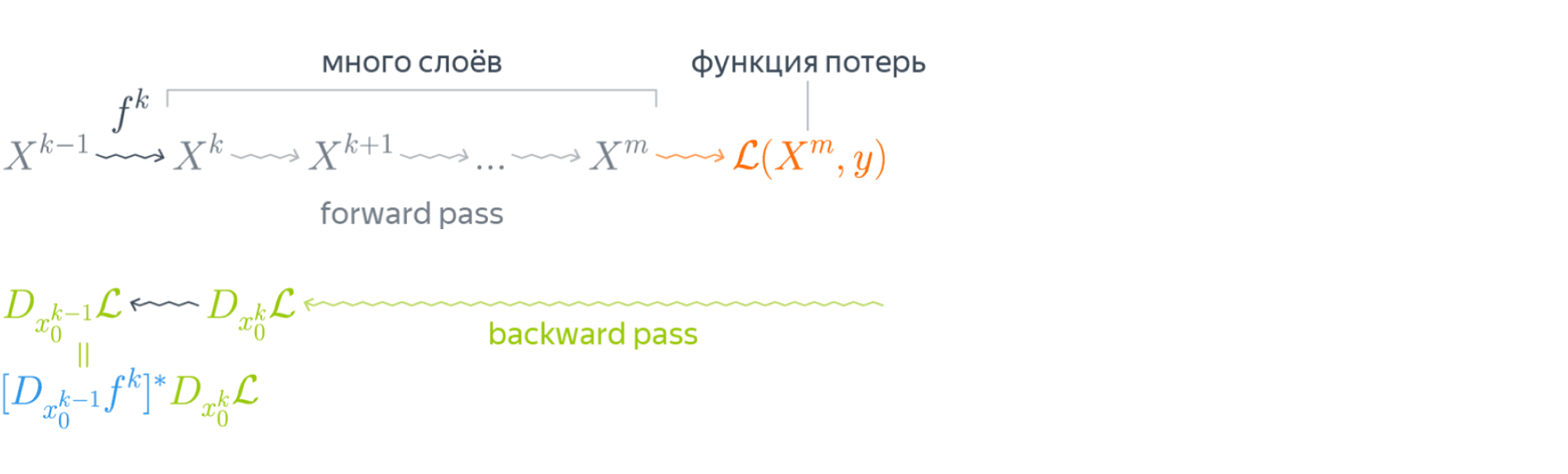
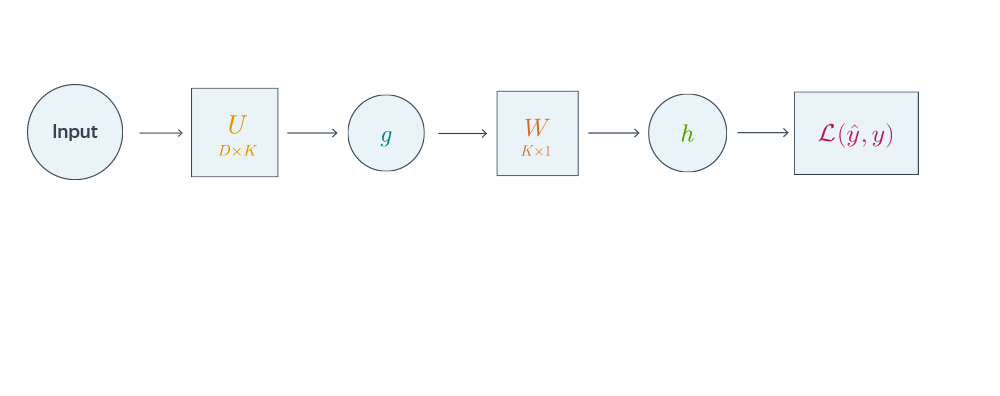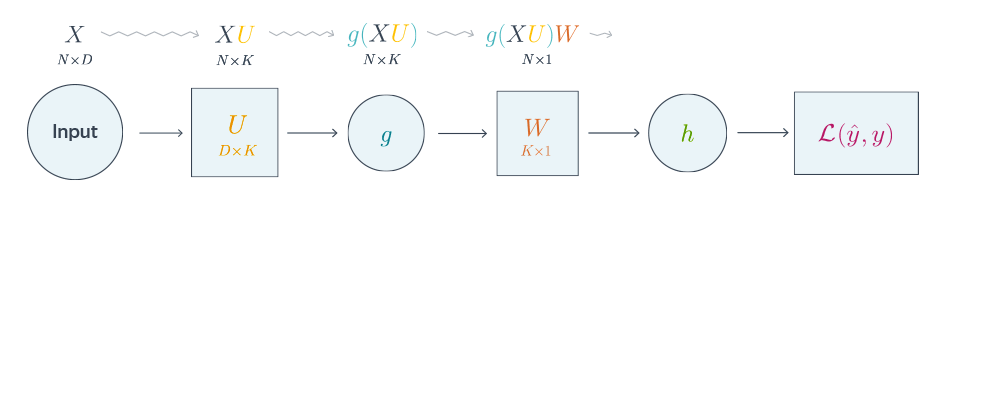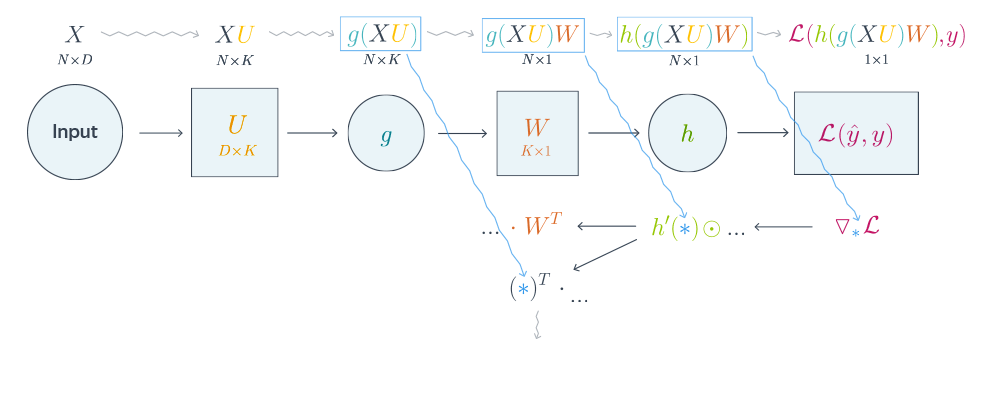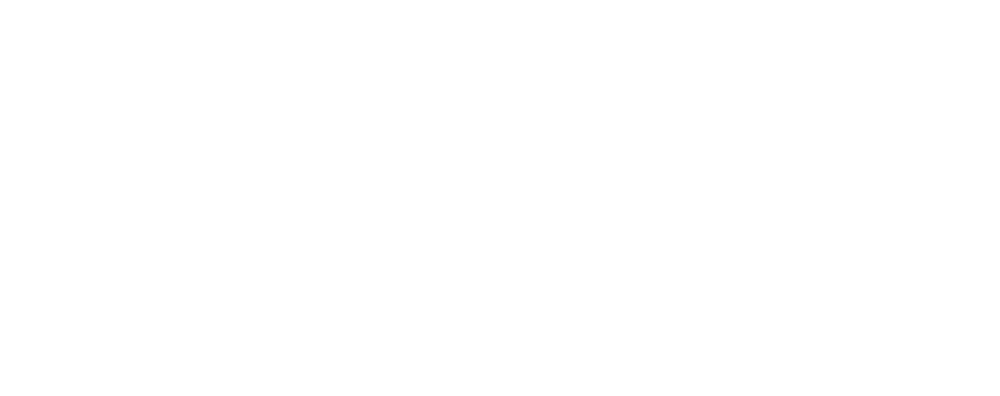

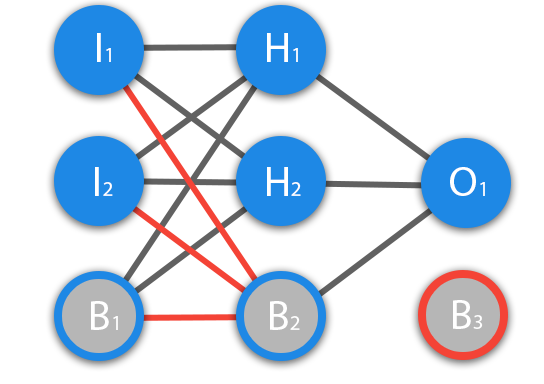

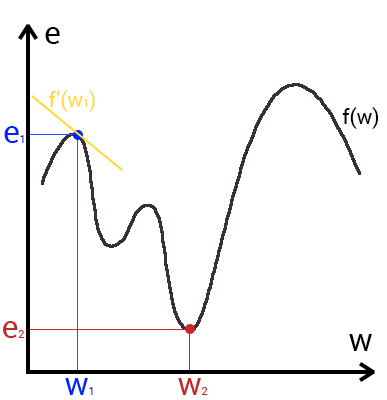

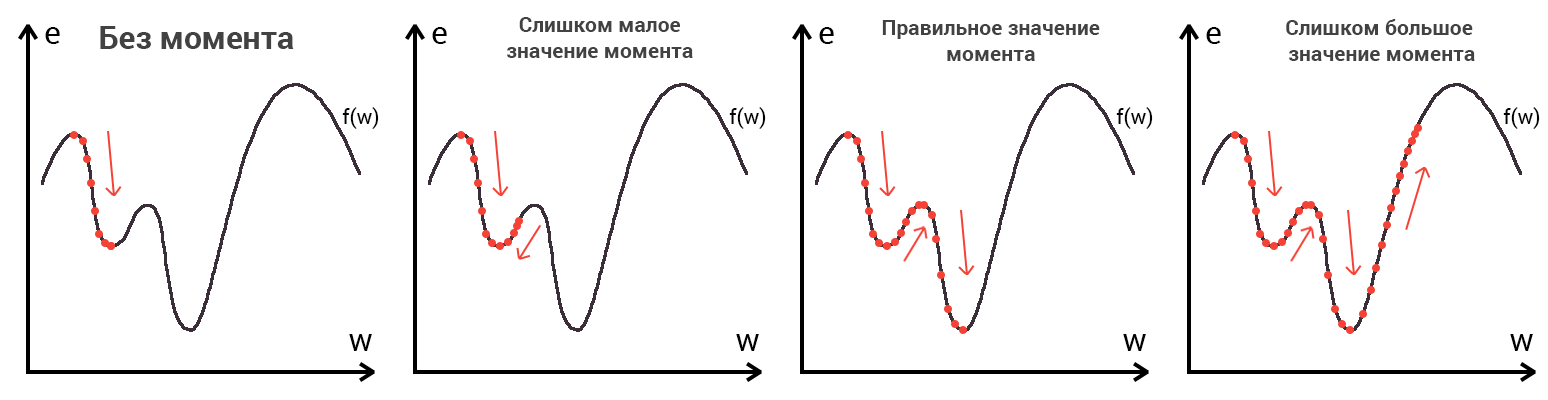
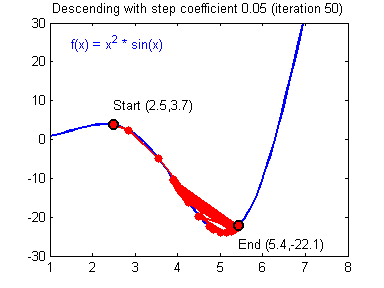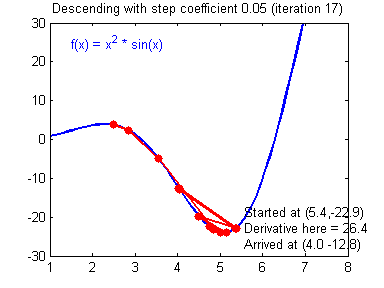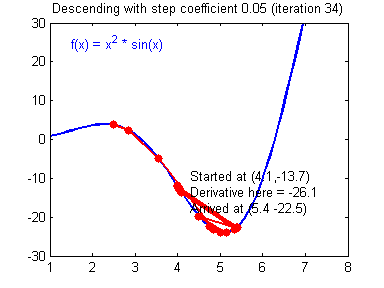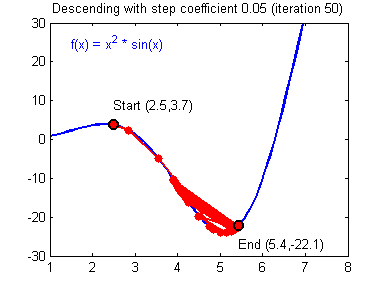

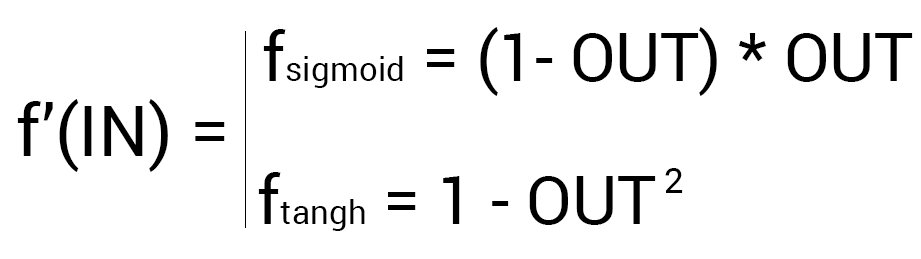
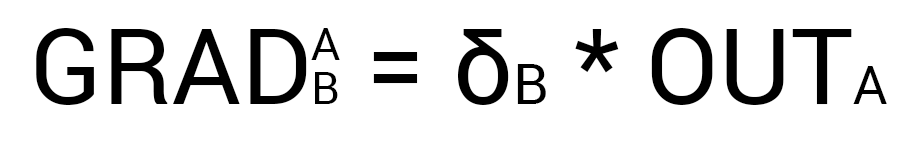

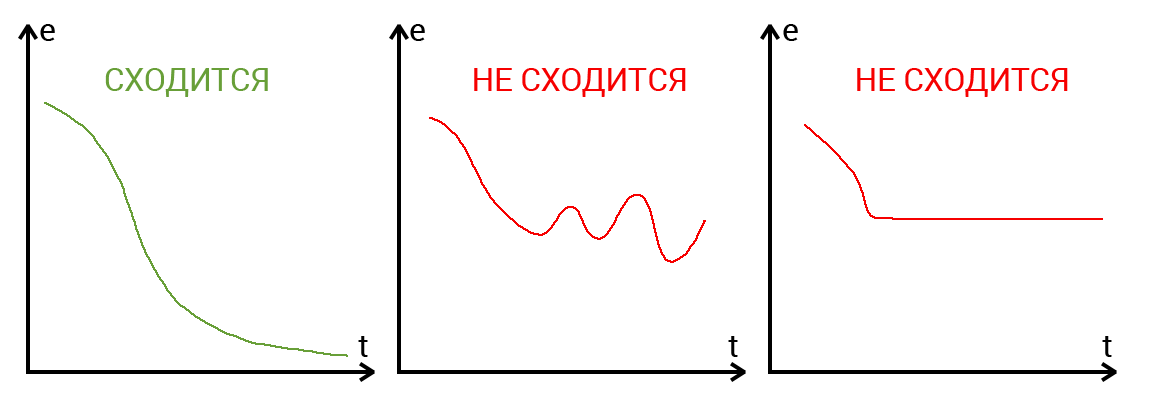
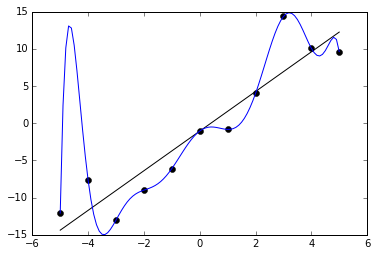
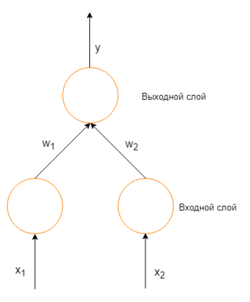
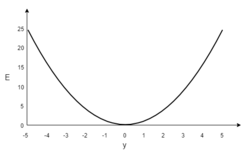
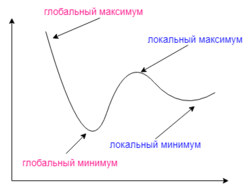
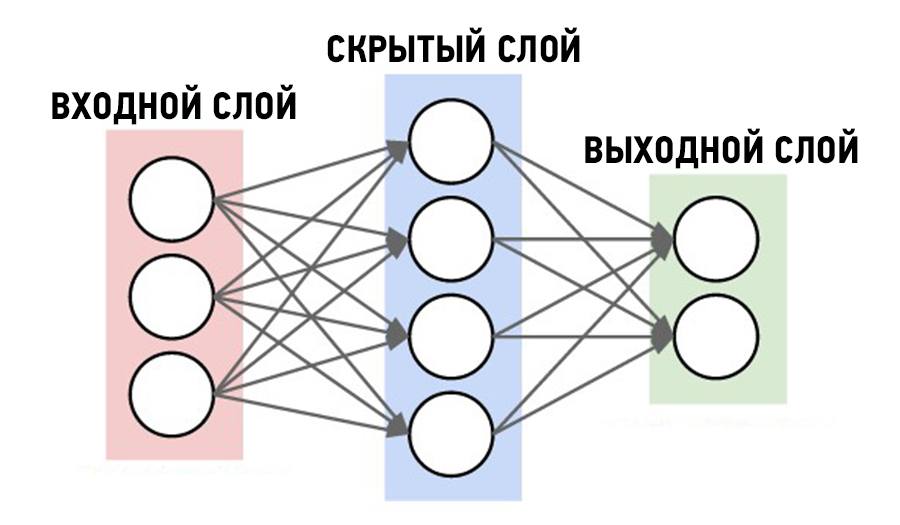
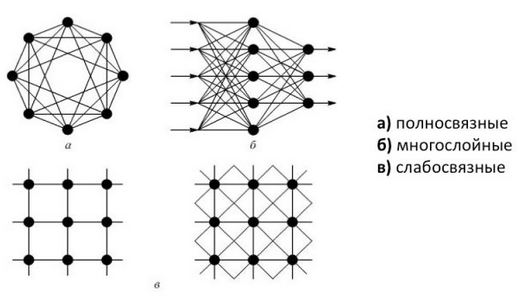
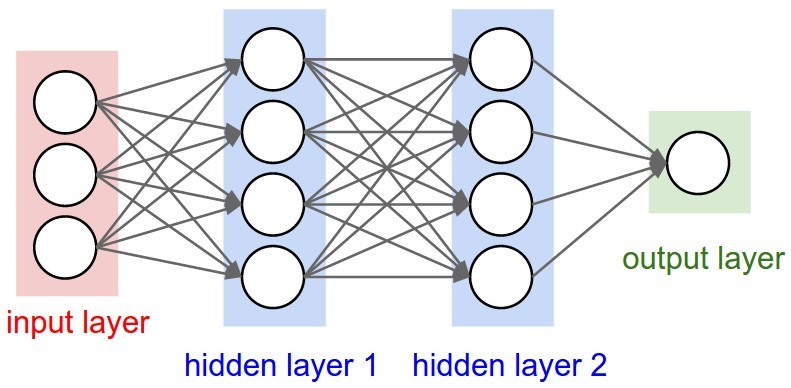
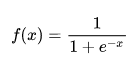
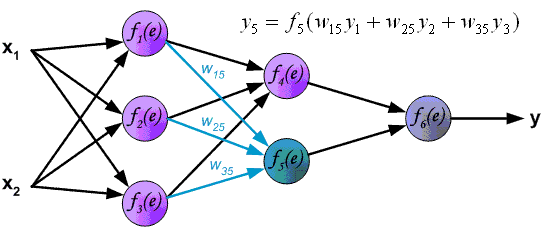
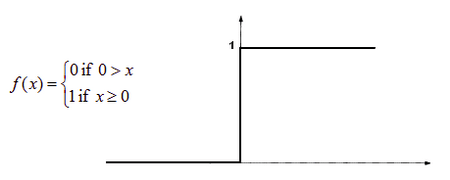
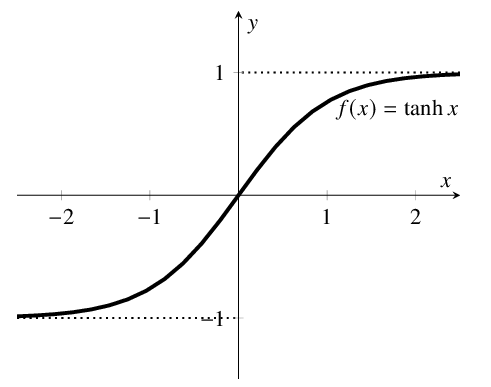
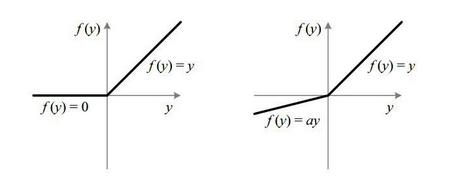
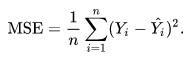
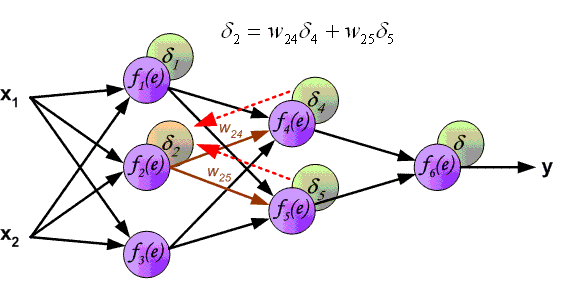
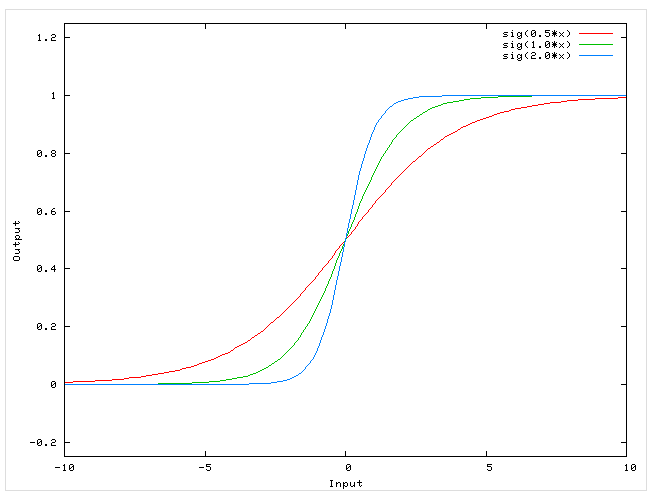
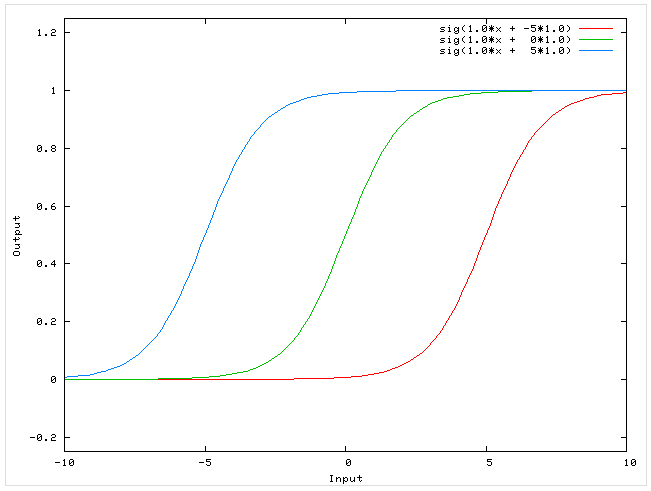


![Пример весов в диапазоне [-1;1]](https://codeby.school/images/immersion_in_ml_part1/16.png)
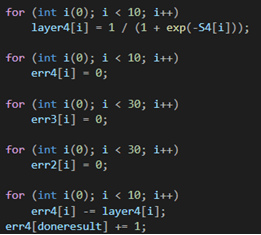


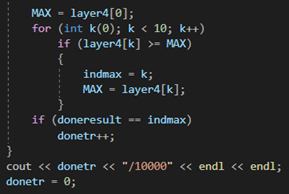
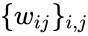 маленькими случайными значениями.
маленькими случайными значениями.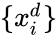 на вход сети и подсчитать выходы
на вход сети и подсчитать выходы 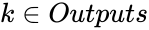
 .
. .
. .
. .
.