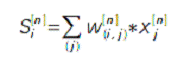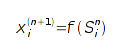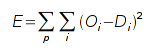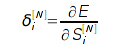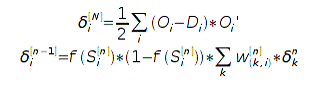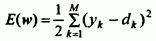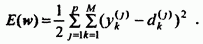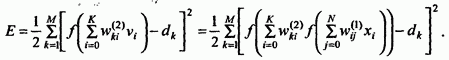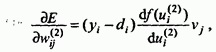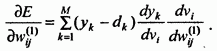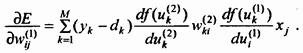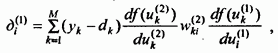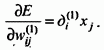Реферат алгоритм обратного распространения ошибки

Алгоритм обратного распространения ошибки

Содержание

Введение

Глава 1. Обучение нейронных сетей

1.1 Общие подходы нейронных сетей

Глава 2. Алгоритм обратного распространения ошибки

2.1 Описание алгоритма обратного распространения ошибки

2.2 Реализация алгоритма обратного распространения ошибки на
примере аппроксимации функции

2.3 Анализ алгоритма обратного распространения ошибки

Список использованной литературы

Введение

В последние несколько лет <#»721503.files/image001.gif»>

Рис 1 — График полинома

Нейронная сеть сталкивается с точно такой же трудностью. Сети с
большим числом весов моделируют более сложные функции и, следовательно, склонны
к переобучению. Сеть же с небольшим числом весов может оказаться недостаточно
гибкой, чтобы смоделировать имеющуюся зависимость. Например, сеть без
промежуточных слоев на самом деле моделирует обычную линейную функцию.

Как же выбрать «правильную» степень сложности для сети?
Почти всегда более сложная сеть дает меньшую ошибку, но это может
свидетельствовать не о хорошем качестве модели, а о переобучении.

Ответ состоит в том, чтобы использовать механизм контрольной
кросс-проверки
<#»721503.files/image002.gif»>

Нелинейность такого вида удобна простотой расчета
производной:

Для обучения сети используется P пар векторов сигналов:
входной вектор I и вектор, который должен быть получен на выходе сети D. Сеть,
в простом случае, состоит из N слоев, причем каждый нейрон последующего слоя
связан со всеми нейронами предыдущего слоя связями, с весами w ^[n].

При прямом распространении, для каждого слоя рассчитывается
(и запоминается) суммарный сигнал на выходе слоя (S ^[n]) и сигнал на
выходе нейрона. Так, сигнал на входе i-го нейрона n-го слоя:

Здесь w (_{i,j) —} веса связей n-го слоя. Сигнал на
выходе нейрона рассчитывается применением к суммарному сигналу нелинейности
нейрона.

Сигнал выходного слоя x ^[N] считается выходным
сигналом сети O.

По выходному сигналу сети O и сигналу D, который должен
получится на выходе сети для данного входа, рассчитываться ошибка сети. Обычно
используется средний квадрат отклонения по всем векторам обучающей выборки:

Для обучения сети используется градиент функции ошибки по
весам сети. Алгоритм обратного распространения предполагает расчет градиента
функции ошибки «обратным распространением сигнала» ошибки. Тогда
частная производная ошибки по весам связей рассчитывается по формуле:

Здесь δ — невязка сети, которая
для выходного слоя рассчитывается по функции ошибки:

А для скрытых слоев — по невязке предыдущего слоя:

Для случая сигмоидной нелинейности и среднего квадрата
отклонения как функции ошибки:

Собственно обучение сети состоит в нахождении таких значений
весов, которые минимизируют ошибку на выходах сети. Существует множество методов,
основанных или использующих градиент, позволяющих решить эту задачу. В
простейшем случае, обучение сети проводится <#»721503.files/image011.gif»>

Такой метод обучения называется «оптимизация методом
градиентного спуска» и, в случае нейросетей, часто считается частью метода
обратного распространения ошибки.

2.2
Реализация алгоритма обратного распространения ошибки на примере аппроксимации
функции

Задание: Пусть имеется таблица значений аргумента (x_i)
и соответствующих значений функции (f (x_i)) (эта таблица
могла возникнуть при вычислениях некоторой аналитически заданной функции при
проведении эксперимента по выявлению зависимости силы тока от сопротивления в
электрической сети, при выявлении связи между солнечной активностью и
количеством обращений в кардиологический центр, между размером дотаций фермерам
и объемом производства сельхозпродукции и т.п.).

В среде Matlab необходимо построить и обучить нейронную сеть
для аппроксимации таблично заданной функции , i=1, 20. Разработать
программу, которая реализует нейросетевой алгоритм аппроксимации и выводит
результаты аппроксимации в виде графиков.

Аппроксимация заключается в том, что, используя имеющуюся
информацию по f (x), можно рассмотреть аппроксимирующую функцию z (x) близкую в
некотором смысле к f (x), позволяющую выполнить над ней соответствующие
операции и получить оценку погрешности такой замены.

Под аппроксимацией обычно подразумевается описание некоторой,
порой не заданной явно, зависимости или совокупности представляющих ее данных с
помощью другой, обычно более простой или более единообразной зависимости. Часто
данные находятся в виде отдельных узловых точек, координаты которых задаются
таблицей данных. Результат аппроксимации может не проходить через узловые
точки. Напротив, задача интерполяции — найти данные в окрестности узловых
точек. Для этого используются подходящие функции, значения которых в узловых
точках совпадают с координатами этих точек [8].

Задача. В среде Matlab необходимо построить и обучить
нейронную сеть для аппроксимации таблично заданной функции (см. рисунок 5).

Рисунок 5. Таблица значений функции В математической среде
Matlab в командном окне записываем код программы создания и обучения нейронной
сети.

Для решения воспользуемся функцией newff (.) — создание
«классической» многослойной НС с обучением по методу обратного
распространения ошибки, т.е. изменение весов синапсов происходит с учетом
функции ошибки, разница между реальными и правильными ответами нейронной сети,
определяемыми на выходном слое, распространяется в обратном направлении —
навстречу потоку сигналов. Сеть будет иметь два скрытых слоя. В первом слое 5 нейронов,
во втором — 1. Функция активации первого слоя — ‘tansig’ (сигмоидная функция,
возвращает выходные векторы со значениями в диапазоне от — 1 до 1), второго —
‘purelin’ (линейная функция активации, возвращает выходные векторы без
изменений). Будет проведено 100 эпох обучения. Обучающая функция ‘trainlm’ —
функция, тренирующая сеть (используется по умолчанию, поскольку она
обеспечивает наиболее быстрое обучение, но требует много памяти) [9].

Код программы:

= zeros (1, 20);i = 1: 20 %создание массива P (i) = i*0.1;
%входные данные (аргумент)  end T= [2.09 2.05 2.19 2.18 2.17 2.27 2.58 2.73
2.82 3.04 3.03 3.45 3.62 3.85 4.19 4.45 4.89 5.06 5.63 5.91]; %входные данные
(значение функции)  net = newff ([-1 2.09], [5 1],{‘tansig’ ‘purelin’});
%создание нейронной сети net. trainParam. epochs = 100; %задание числа эпох
обучения net=train (net,P,T); %обучение сети y = sim (net,P); %опрос обученной
сети figure (1);

hold on;(‘P’);(‘T’);

plot (P,T,P,y,’o’),grid; %прорисовка графика исходных данных
и функции, сформированной нейронной сетью.

Результат работы нейронной сети.

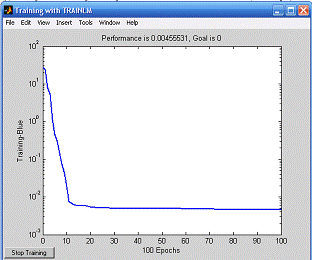
Результат обучения (см. рис.2): график показывает время
обучения нейронной сети и ошибку обучения. В этом примере нейронная сеть прошла
все 100 эпох постепенно обучаясь и уменьшая ошибки, дошла до 10^-2,35
(0,00455531).

Рисунок 2. Результат обучения нейронной сети

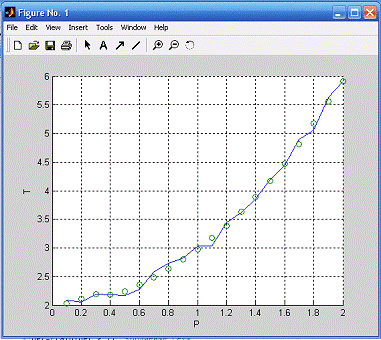
График исходных данных и функции, сформированной нейронной
сетью (см. рис.3): кружками обозначены исходные данные, а линия — функция,
сформированная нейронной сетью. Далее по полученным точкам можно построить
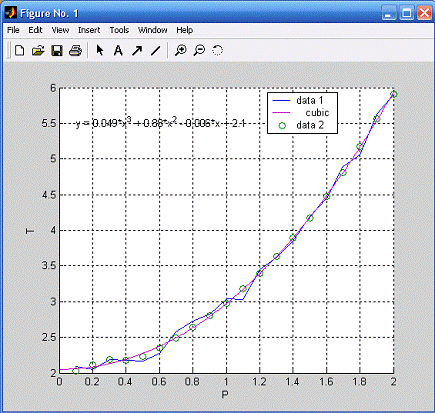
регрессию и получить уравнение аппроксимации (см. рисунок 8). Мы использовали
кубическую регрессию, так как ее график наиболее точно проходит через
полученные точки. Полученное уравнение имеет вид:

=0.049x³+0.88x²-0.006x+2.1.

Таким образом, видим, что используя нейронную сеть, можно
довольно быстро найти функцию, зная лишь координаты точек, через которые она
проходит.

Рисунок 3. График исходных данных и функции, сформированной
нейронной  сетью

Рисунок 4. График функции аппроксимации

2.3 Анализ
алгоритма обратного распространения ошибки

Алгоритм обратного распространения ошибки осуществляет так
называемый градиентный спуск по поверхности ошибок. Не углубляясь, это означает
следующее: в данной точке поверхности находится направление скорейшего спуска,
затем делается прыжок вниз на расстояние, пропорциональное коэффициенту
скорости обучения и крутизне склона, при этом учитывается инерция, то есть
стремление сохранить прежнее направление движения. Можно сказать, что метод
ведет себя как слепой кенгуру — каждый раз прыгает в направлении, которое
кажется ему наилучшим. На самом деле шаг спуска вычисляется отдельно для всех
обучающих наблюдений, взятых в случайном порядке, но в результате получается
достаточно хорошая аппроксимация спуска по совокупной поверхности ошибок.

Несмотря на достаточную простоту и применимость в решении
большого круга задач, алгоритм обратного распространения ошибки имеет ряд
серьезных недостатков. Отдельно стоит отметить неопределенно долгий процесс
обучения. В сложных задачах для обучения сети могут потребоваться дни или даже
недели, а иногда она может и вообще не обучиться. Это может произойти из-за следующих
нижеописанных факторов.

1. Паралич сети

В процессе обучения сети, значения весов могут в результате
коррекции стать очень большими величинами. Это может привести к тому, что все
или большинство нейронов будут выдавать на выходе сети большие значения, где
производная функции активации от них будет очень мала. Так как посылаемая
обратно в процессе обучения ошибка пропорциональна этой производной, то процесс
обучения может практически замереть. В теоретическом отношении эта проблема
плохо изучена. Обычно этого избегают уменьшением размера шага (скорости
обучения), но это увеличивает время обучения. Различные эвристики
использовались для предохранения от паралича или для восстановления после него,
но пока что они могут рассматриваться лишь как экспериментальные.

2. Локальные минимумы

Как говорилось вначале, алгоритм обратного распространения
ошибки использует разновидность градиентного спуска, т.е. осуществляет спуск
вниз по поверхности ошибки, непрерывно подстраивая веса в направлении к
минимуму. Поверхность ошибки сложной сети сильно изрезана и состоит из холмов,
долин, складок и оврагов в пространстве высокой размерности. Сеть может попасть
в локальный минимум (неглубокую долину), когда рядом имеется более глубокий
минимум. В точке локального минимума все направления ведут вверх, и сеть
неспособна из него выбраться. Статистические методы обучения могут помочь
избежать этой ловушки, но они медленны.

3. Размер шага

Алгоритм обратного распространения ошибки имеет
доказательство своей сходимости. Это доказательство основывается на том, что
коррекция весов предполагается бесконечно малой. Ясно, что это неосуществимо на
практике, так как ведет к бесконечному времени обучения. Размер шага должен
браться конечным, и в этом вопросе приходится опираться только на опыт. Если
размер шага очень мал, то сходимость слишком медленная, если же очень велик, то
может возникнуть паралич или постоянная неустойчивость.

4. Временная неустойчивость

Если сеть учится распознавать буквы, то нет смысла учить
«Б», если при этом забывается «А». Процесс обучения должен
быть таким, чтобы сеть обучалась на всем обучающем множестве без пропусков
того, что уже выучено. В доказательстве сходимости это условие выполнено, но
требуется также, чтобы сети предъявлялись все векторы обучающего множества
прежде, чем выполняется коррекция весов. Необходимые изменения весов должны
вычисляться на всем множестве, а это требует дополнительной памяти; после ряда
таких обучающих циклов веса сойдутся к минимальной ошибке. Этот метод может
оказаться бесполезным, если сеть находится в постоянно меняющейся внешней
среде, так что второй раз один и тот же вектор может уже не повториться. В этом
случае процесс обучения может никогда не сойтись, бесцельно блуждая или сильно
осциллируя. В этом смысле алгоритм обратного распространения ошибки не похож на
биологические системы.

Заключение Нейронные сети хорошо осуществляют сглаживание или
подбор значений функций по точкам. Нейронные сети могут подобрать большинство
функций. Причем, это могут быт как функции одной переменной, так и нескольких.

В данной курсовой работе было представлено, каким образом
нейронные сети способны помочь людям в генерации знаний, которые основывались
бы на всех первоначальных данных. Исследования в области нейронных сетей в
основном достаточно наглядны. По сравнению с другими вычислительными методами в
статистике и науке они имеют значительные преимущества. Так, у моделей на
основе нейронных сетей очень гибкие теоретические требования; кроме того, им
необходимы совсем небольшие объемы предварительных знаний относительно
формирования задачи.

В соответствии с задачами в курсовой работе было выполнено
следующее.

. Проведен обзор алгоритмов обучения нейронных сетей.

. Рассмотрены методы ускорения обучения нейронной сети.

. Изучены области применения нейронных сетей.

. Рассмотрен алгоритм обратного распространения ошибки.

. Реализован алгоритм обратного распространения ошибки на
примере аппроксимации функции.

В ходе выполнения данной курсовой работы была построена и
обучена нейронная сеть для аппроксимации таблично заданной функции , i=1,20 в среде Matlab.
Разработана программа, которая реализует нейросетевой алгоритм аппроксимации и
выводит результаты аппроксимации в виде графиков.

Для решения использована функция newff (.) — создание
«классической» многослойной НС с обучением по методу обратного
распространения ошибки.

Как мощный механизм обучения нейронные сети могут широко
применяться в различных областях. Существует, однако, возможность недоразумений
в оценке методик машинного обучения. Они никогда не смогут полностью заменить
людей в процессе решения задачи. Нейронные сети должны использоваться для
обобщения данных, а не для определения, атрибуты и критерии которого весьма
важны при сборе данных. Нейронные сети адаптивны по своей природе, они могут
подражать решению проблемы человеком, но они не сообщат нам, какой из критериев
решения задачи должен быть принят во внимание перед сбором данных. Кроме того,
обучающиеся машины часто используются при формализации знаний из данных
реального мира, но сами обучающиеся машины не могут генерировать принципы
формализации.

Список
использованной литературы

1. Бестенс Д.,
Ван ден Берг, Вуд Д. Нейронные сети и финансовые рынки. — М.: Диалектика
<http://ru.wikipedia.org/w/index.php?title=%D0%94%D0%B8%D0%B0%D0%BB%D0%B5%D0%BA%D1%82%D0%B8%D0%BA%D0%B0_(%D0%B8%D0%B7%D0%B4%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D1%81%D1%82%D0%B2%D0%BE)&action=edit&redlink=1>,
2009. — 224 с.

. Вороновский
Г.К. Махотило К.В. Петрашев С.Н. Сергеев С.А. — Генетические алгоритмы,
искусственные нейронные сети и проблемы виртуальной реальности — СПб.:
БХВ-Петербург
<http://ru.wikipedia.org/wiki/%D0%91%D0%A5%D0%92-%D0%9F%D0%B5%D1%82%D0%B5%D1%80%D0%B1%D1%83%D1%80%D0%B3>,
2007. — 544 с.

. Горбань А. Н,
Хлебопрос Р.Г. Демон Дарвина. Идея оптимальности и естественный отбор —
Вильямс, 2011. — 83 с.

. Горбань А. Н,
Дунин-Барковский, Кирдин А.Н. Нейроинформатика. МЦНМО, 2010. — 143 с.

5. Заенцев И. В Нейронные
сети. Основные модели. — ВГУ. 2011. — 321c.

6.
Федотов В.Х. Нейронные сети в экономике Чебоксары, 2006. — 171с.

.
http://ru. wikipedia.org/wiki/Нейронная_сеть

.
http://www.statsoft.ru/HOME/TEXTBOOK/modules/stneunet.html

9. http://mechanoid. narod.ru/nns/base/index.html#golovko

. http://www.scorcher.ru/neuro/science/neurocomp/mem52. htm

. http://www.neuroproject.ru/neuro. php

Алгоритм обратного
распространения ошибки определяет
стратегию подбора весов многослойной
сети с применением градиентных методов
оптимизации. «Изобретенный заново»
несколько раз, он в настоящее время
считается одним из наиболее эффективных
алгоритмов обучения многослойной сети.
Его основу составляет целевая функция,
формулируемая, как правило, в виде
квадратичной суммы разностей между
фактическими и ожидаемыми значениями
выходных сигналов.

В случае единичной
обучающей выборки (x,
d)
целевая функция определяется в виде

(51)

При большем
количестве обучающих выборок j
(j=1,
2, …, p)
целевая функция превращается в сумму
по всем выборкам

(52)

Уточнение весов
может проводиться после предъявления
каждой обучающей выборки (так называемый
режим “онлайн”) либо однократно после
предъявления всех выборок, составляющих
цикл обучения (режим “оффлайн”). В
последующем изложении используется
целевая функция вида (51), которая
соответствует актуализации весов после
предъявления каждой выборки.

1. Для упрощения
   можно считать, что цель обучения состоит
   в таком определении значений весов
   нейронов каждого слоя сети, чтобы при
   заданном входном векторе получить на
   выходе значения сигналов y_i,
   совпадающие с требуемой точностью с
   ожидаемыми значениями d_i
   при i=1,
   2, …, M.

47. Этапы алгоритма обратного распространения ошибки

Обучение
сети с использованием алгоритма обратного
распространения ошибки проводится в
несколько этапов.
На первом из них предъявляется обучающая
выборка х
и рассчитываются значения сигналов
соответствующих нейронов сети. При
заданном векторе x
определяются вначале значения выходных
сигналов v_i
скрытого слоя, а затем значения y_i
нейронов выходного слоя. Для расчета
применяются формулы (49) и (50).

После получения
значений выходных сигналов y_i
становится возможным рассчитать
фактическое значение целевой функции
E(w)
заданной выражением (51). На втором этапе
минимизируется значение этой функции.

48. Градиентные алгоритмы обучения сети

Если принять, что
целевая функция непрерывна, то наиболее
эффективными способами обучения
оказываются градиентные методы
оптимизации,
согласно которым уточнение вектора
весов (обучение) производится по
формуле

где η
– коэффициент обучения, p(w)
– направление в многомерном пространстве
w.

Обучение
многослойной сети с применением
градиентных методов
требует определения вектора градиента
относительно весов всех слоев сети, что
необходимо для правильного выбора
направления p(w).
Эта задача имеет очевидное решение
только для весов выходного слоя. Для
других слоев создана специальная
стратегия, которая в теории ИНС называется
алгоритмом обратного распространения
ошибки (error
backpropagation),
отождествляемым, как правило, с процедурой
обучения сети. В соответствии с этим
алгоритмом в каждом цикле обучения
выделяются следующие этапы:

1. А
   нализ
   нейронной сети в прямом направлении
   передачи информации при генерации
   входных сигналов, составляющих очередной
   вектор х.
   В результате такого анализа рассчитываются
   значения выходных сигналов нейронов
   скрытых слоев и выходного слоя, а также
   соответствующие производные

функции активации
каждого слоя, где m
– количество слоев сети.

2. Создание сети
обратного распространения ошибок путем
изменения направлений передачи сигналов,
замена функций активации их производными
и подача на бывший выход (а в настоящий
момент — вход) сети возбуждения в виде
разности между фактическим и ожидаемым
значением. Для определенной таким
образом сети необходимо рассчитать
значения требуемых обратных разностей.

3. Уточнение весов
(обучение сети) производится по
предложенным выше формулам на основе
результатов, полученных в п. 1 и 2, для
оригинальной сети и для сети обратного
распространения ошибки.

4. Описанный в п.
1, 2 и 3 процесс следует повторить для
всех обучающих выборок, продолжая его
вплоть до выполнения условия остановки
алгоритма. Действие алгоритма завершается
в момент, когда норма градиента упадет
ниже априори заданного значения ε
характеризующего точность процесса
обучения.

Для сети с одним
скрытым слоем

Рассмотрим условия,
относящиеся к сети с одним скрытым
слоем. Используемые обозначения
представлены на рис. 19 (уже был ранее).

Как и ранее,
количество входных узлов обозначим
буквой N
количество нейронов в скрытом слое К,
а количество нейронов в выходном слое
М.
Будем использовать сигмоидальную
функцию активации этих нейронов. Основу
алгоритма составляет расчет значения
целевой функции как квадратичной суммы
разностей между фактическими и ожидаемыми
значениями выходных сигналов сети. В
случае единичной обучающей выборки
(x,d)
целевая функция задается формулой (51),
а для множества обучающих выборок j
(j=1,
2, …, p)
– формулой (52).

Для упрощения
излагаемого материала будем использовать
целевую функцию вида (51), которая позволяет
уточнять веса после предъявления каждой
обучающей выборки.

Эта функция
определяется выражением:

(53)

Конкретные
компоненты градиента рассчитываются
дифференцированием этой зависимости.
В первую очередь подбираются веса
нейронов выходного слоя. Для выходных
весов получаем:

где

Если ввести
обозначение (54)

то соответствующий
компонент градиента относительно весов
нейронов выходного слоя можно представить
в виде

(55)

Компоненты
градиента относительно нейронов скрытого
слоя определяются по тому же принципу,
однако они описываются другой, более
сложной зависимостью, следующей из
существования функции, заданной в виде

(56)

После конкретизации
отдельных составляющих этого выражения
получаем:

(57)

Если ввести
обозначение

(58)

то получим выражение,
определяющее компоненты градиента
относительно весов нейронов скрытого
слоя в виде

(59)

В обоих случаях
(формулы (55) и (59)) описание градиента
имеет аналогичную структуру и
представляется произведением двух
сигналов: первый соответствует начальному
узлу данной взвешенной связи, а второй
– величине погрешности, перенесенной
на узел, с которым эта связь установлена.
Определение вектора градиента очень
важно для последующего процесса уточнения
весов.

В классическом
алгоритме обратного распространения
ошибки фактор p(w)
задает направление отрицательного
градиента, поэтому

(60)

Существуют и
другие, более эффективные методы выбора
направления p(w).

Градиентные
методы обучения сети

• Алгоритм
  наискорейшего спуска

• Алгоритм переменной
  метрики

• Алгоритм
  Левенберга-Марквардта

• Алгоритм сопряженных
  градиентов

А также:

• Эвристические
  методы обучения сети

• Элементы глобальной
  оптимизации:

  • Алгоритм имитации
    отжига

  • Генетические
    алгоритмы

• Методы инициализации
  весов

РАДИАЛЬНЫЕ
НЕЙРОННЫЕ СЕТИ

Многослойные
нейронные сети, представленные в
предыдущих разделах, с точки зрения
математики выполняют аппроксимацию
стохастической функции нескольких
переменных путем преобразования
множества входных переменных во
множество выходных переменных .
Вследствие характера сигмоидальной
функции активации осуществляется
аппроксимация глобального типа. В
результате ее нейрон, который был однажды
включен (после превышения суммарным
сигналом u_i
определенного
порогового значения), остается в этом
состоянии при любом значении u_i,
превышающем этот порог. Поэтому всякий
раз преобразование значения функции в
произвольной точке пространства
выполняется объединенными усилиями
многих нейронов, что и объясняет название
глобальная
аппроксимация.

Другой способ
отображения входного множества в
выходное заключается в преобразовании
путем адаптации нескольких одиночных
аппроксимирующих функций к ожидаемым
значениям, причем эта адаптация проводится
только в ограниченной области
многомерного пространства. При таком
подходе отображение всего множества
данных представляет собой сумму локальных
преобразований. С учетом роли, которую
играют скрытые нейроны, они составляют
множество базисных функций локального
типа. Выполнение одиночных функций (при
ненулевых значениях) регистрируется
только в ограниченной области пространства
данных – отсюда и название локальная
аппроксимация.

Особое семейство
образуют сети с радиальной базисной
функцией, в которых скрытые нейроны
реализуют функции, радиально изменяющиеся
вокруг выбранного центра и принимающие
ненулевые значения только в окрестности
этого центра. Подобные функции,
определяемые в виде φ(x)=
φ(||x—c||)
будем называть радиальными
базисными функциями.
В таких сетях роль скрытого нейрона
заключается в отображении радиального
пространства вокруг одиночной заданной
точки либо вокруг группы таких точек,
образующих кластер. Суперпозиция
сигналов, поступающих от всех скрытых
нейронов, которая выполняется выходным
нейроном, позволяет получить отображение
всего многомерного пространства.

Сети
радиального типа представляют собой
естественное дополнение сигмоидальных
сетей. Сигмоидальный нейрон представляется
в многомерном пространстве гиперплоскостью,
которая разделяет это пространство на
две категории (два класса), в которых
выполняется одно из двух условий: либо
либо

Такой подход
продемонстрирован на рис. 20 а).

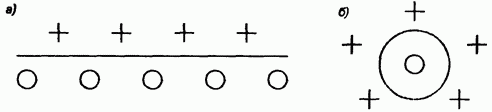
Рис. 20. Иллюстрация способов разделения
пространства данных:

а) сигмоидальным нейроном; б) радиальным
нейроном

В свою очередь
радиальный нейрон представляет собой
гиперсферу, которая осуществляет шаровое
разделение пространства вокруг
центральной точки (рис. 20 б). Именно с
этой точки зрения он является естественным
дополнением сигмоидального нейрона,
поскольку в случае круговой симметрии
данных позволяет заметно уменьшить
количество нейронов, необходимых для
разделения различных классов.

Поскольку нейроны
могут выполнять различные функции, в
радиальных сетях отсутствует необходимость
использования большого количества
скрытых слоев. Структура типичной
радиальной сети включает входной слой,
на который подаются сигналы, описываемые
входным вектором х,
скрытый слой с нейронами радиального
типа и выходной слой, состоящий, как
правило, из одного или нескольких
линейных нейронов. Функция выходного
нейрона сводится исключительно к
взвешенному суммированию сигналов,
генерируемых скрытыми нейронами.

Знакомимся с методом обратного распространения ошибки

Всем привет! Новогодние праздники подошли к концу, а это значит, что мы вновь готовы делиться с вами полезным материалом. Перевод данной статьи подготовлен в преддверии запуска нового потока по курсу «Алгоритмы для разработчиков».

Метод обратного распространения ошибки – вероятно самая фундаментальная составляющая нейронной сети. Впервые он был описан в 1960-е и почти 30 лет спустя его популяризировали Румельхарт, Хинтон и Уильямс в статье под названием «Learning representations by back-propagating errors».

Метод используется для эффективного обучения нейронной сети с помощью так называемого цепного правила (правила дифференцирования сложной функции). Проще говоря, после каждого прохода по сети обратное распространение выполняет проход в обратную сторону и регулирует параметры модели (веса и смещения).

В этой статья я хотел бы подробно рассмотреть с точки зрения математики процесс обучения и оптимизации простой 4-х слойной нейронной сети. Я считаю, что это поможет читателю понять, как работает обратное распространение, а также осознать его значимость.

Определяем модель нейронной сети

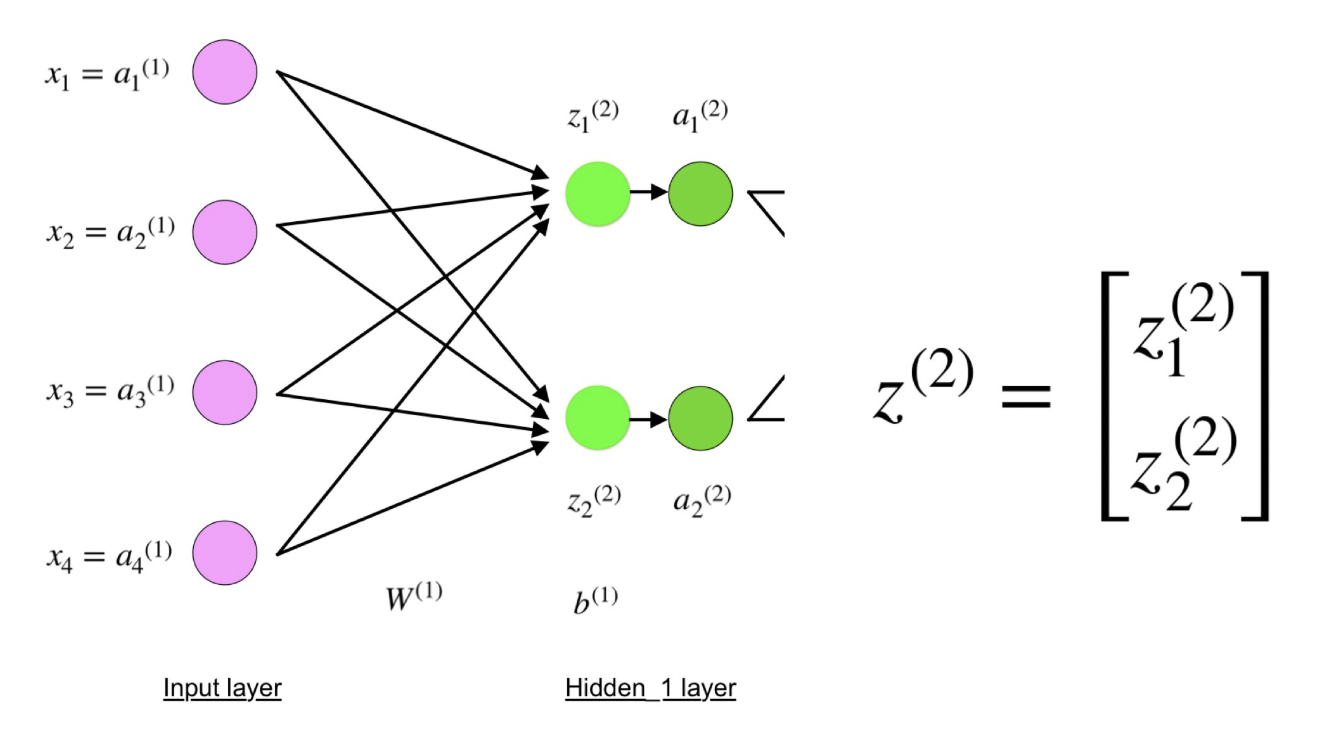
Четырехслойная нейронная сеть состоит из четырех нейронов входного слоя, четырех нейронов на скрытых слоях и 1 нейрона на выходном слое.

Простое изображение четырехслойной нейронной сети.

Входной слой

На рисунке нейроны фиолетового цвета представляют собой входные данные. Они могут быть простыми скалярными величинами или более сложными – векторами или многомерными матрицами.

Уравнение, описывающее входы xi.

Первый набор активаций (а) равен входным значениям. «Активация» — это значение нейрона после применения функции активации. Подробнее смотрите ниже.

Скрытые слои

Конечные значения в скрытых нейронах (на рисунке зеленого цвета) вычисляются с использованием z^l – взвешенных входов в слое I и a^I активаций в слое L. Для слоев 2 и 3 уравнения будут следующими:

Для l = 2:

Для l = 3:

W² и W³ – это веса на слоях 2 и 3, а b² и b³ – смещения на этих слоях.

Активации a² и a³ вычисляются с помощью функции активации f. Например, эта функция f является нелинейной (как сигмоид, ReLU и гиперболический тангенс) и позволяет сети изучать сложные паттерны в данных. Мы не будем подробно останавливаться на том, как работают функции активации, но, если вам интересно, я настоятельно рекомендую прочитать эту замечательную статью.

Присмотревшись внимательно, вы увидите, что все x, z², a², z³, a³, W¹, W², b¹ и b² не имеют нижних индексов, представленных на рисунке четырехслойной нейронной сети. Дело в том, что мы объединили все значения параметров в матрицы, сгруппированные по слоям. Это стандартный способ работы с нейронными сетями, и он довольно комфортный. Однако я пройдусь по уравнениям, чтобы не возникло путаницы.

Давайте возьмем слой 2 и его параметры в качестве примера. Те же самые операции можно применить к любому слою нейронной сети.
W¹ – это матрица весов размерности (n, m), где n – это количество выходных нейронов (нейронов на следующем слое), а m – число входных нейронов (нейронов в предыдущем слое). В нашем случае n = 2 и m = 4.

Здесь первое число в нижнем индексе любого из весов соответствует индексу нейрона в следующем слое (в нашем случае – это второй скрытый слой), а второе число соответствует индексу нейрона в предыдущем слое (в нашем случае – это входной слой).

x – входной вектор размерностью (m, 1), где m – число входных нейронов. В нашем случае m = 4.

b¹ – это вектор смещения размерности (n, 1), где n – число нейронов на текущем слое. В нашем случае n = 2.

Следуя уравнению для z² мы можем использовать приведенные выше определения W¹, x и b¹ для получения уравнения z²:

Теперь внимательно посмотрите на иллюстрацию нейронной сети выше:

Как видите, z² можно выразить через z₁² и z₂², где z₁² и z₂² – суммы произведений каждого входного значения xⁱ на соответствующий вес W_ij¹.

Это приводит к тому же самому уравнению для z² и доказывает, что матричные представления z², a², z³ и a³ – верны.

Выходной слой

Последняя часть нейронной сети – это выходной слой, который выдает прогнозируемое значение. В нашем простом примере он представлен в виде одного нейрона, окрашенного в синий цвет и рассчитываемого следующим образом:

И снова мы используем матричное представление для упрощения уравнения. Можно использовать вышеприведенные методы, чтобы понять лежащую в их основе логику.

Прямое распространение и оценка

Приведенные выше уравнения формируют прямое распространение по нейронной сети. Вот краткий обзор:

(1) – входной слой
(2) – значение нейрона на первом скрытом слое
(3) – значение активации на первом скрытом слое
(4) – значение нейрона на втором скрытом слое
(5) – значение активации на втором скрытом уровне
(6) – выходной слой

Заключительным шагом в прямом проходе является оценка прогнозируемого выходного значения s относительно ожидаемого выходного значения y.

Выходные данные y являются частью обучающего набора данных (x, y), где x – входные данные (как мы помним из предыдущего раздела).

Оценка между s и y происходит через функцию потерь. Она может быть простой как среднеквадратичная ошибка или более сложной как перекрестная энтропия.

Мы назовем эту функцию потерь С и обозначим ее следующим образом:

Где cost может равняться среднеквадратичной ошибке, перекрестной энтропии или любой другой функции потерь.

Основываясь на значении С, модель «знает», насколько нужно скорректировать ее параметры, чтобы приблизиться к ожидаемому выходному значению y. Это происходит с помощью метода обратного распространения ошибки.

Обратное распространение ошибки и вычисление градиентов

Опираясь на статью 1989 года, метод обратного распространения ошибки:

Постоянно настраивает веса соединений в сети, чтобы минимизировать меру разности между фактическим выходным вектором сети и желаемым выходным вектором.
и
…дает возможность создавать полезные новые функции, что отличает обратное распространение от более ранних и простых методов…

Другими словами, обратное распространение направлено на минимизацию функции потерь путем корректировки весов и смещений сети. Степень корректировки определяется градиентами функции потерь по отношению к этим параметрам.

Возникает один вопрос: Зачем вычислять градиенты?

Чтобы ответить на этот вопрос, нам сначала нужно пересмотреть некоторые понятия вычислений:

Градиентом функции С(x¹, x², …, x^m) в точке x называется вектор частных производных С по x.

Производная функции С отражает чувствительность к изменению значения функции (выходного значения) относительно изменения ее аргумента х (входного значения). Другими словами, производная говорит нам в каком направлении движется С.

Градиент показывает, насколько необходимо изменить параметр x (в положительную или отрицательную сторону), чтобы минимизировать С.

Вычисление этих градиентов происходит с помощью метода, называемого цепным правилом.
Для одного веса (w^jk)_l градиент равен:

(1) Цепное правило
(2) По определению m – количество нейронов на l – 1 слое
(3) Вычисление производной
(4) Окончательное значение
Аналогичный набор уравнений можно применить к (b^j)_l:

(1) Цепное правило
(2) Вычисление производной
(3) Окончательное значение
Общая часть в обоих уравнениях часто называется «локальным градиентом» и выражается следующим образом:

«Локальный градиент» можно легко определить с помощью правила цепи. Этот процесс я не буду сейчас расписывать.

Градиенты позволяют оптимизировать параметры модели:

Пока не будет достигнут критерий остановки выполняется следующее:

Алгоритм оптимизации весов и смещений (также называемый градиентным спуском)

• Начальные значения w и b выбираются случайным образом.
• Эпсилон (e) – это скорость обучения. Он определяет влияние градиента.
• w и b – матричные представления весов и смещений.
• Производная C по w или b может быть вычислена с использованием частных производных С по отдельным весам или смещениям.
• Условие завершение выполняется, как только функция потерь минимизируется.

Заключительную часть этого раздела я хочу посвятить простому примеру, в котором мы рассчитаем градиент С относительно одного веса (w²²)₂.

Давайте увеличим масштаб нижней части вышеупомянутой нейронной сети:

Визуальное представление обратного распространения в нейронной сети
Вес (w²²)₂ соединяет (a²)₂ и (z²)₂, поэтому вычисление градиента требует применения цепного правила на (z³)₂ и (a³)₂:

Вычисление конечного значения производной С по (a²)₃ требует знания функции С. Поскольку С зависит от (a²)₃, вычисление производной должно быть простым.

Я надеюсь, что этот пример сумел пролить немного света на математику, стоящую за вычислением градиентов. Если захотите узнать больше, я настоятельно рекомендую вам посмотреть Стэндфордскую серию статей по NLP, где Ричард Сочер дает 4 замечательных объяснения обратного распространения.

Заключительное замечание

В этой статье я подробно объяснил, как обратное распространение ошибки работает под капотом с помощью математических методов, таких как вычисление градиентов, цепное правило и т.д. Знание механизмов этого алгоритма укрепит ваши знания о нейронных сетях и позволит вам чувствовать себя комфортно при работе с более сложными моделями. Удачи вам в путешествии по глубокому обучению!

На этом все. Приглашаем всех на бесплатный вебинар по теме «Дерево отрезков: просто и быстро».

Реферат: Алгоритм обратного распространения ошибки для адаптивных сетей

Рассмотрим алгоритм обратного распространения ошибки для адаптивных сетей (рис.2.46). Напомним, что сеть имеет L слоев ( l =0,1,…,L) и l = 0 представляет входной слой. Слой l имеет N(l) вершин. Выходное значение вершины зависит от входных значений и параметров функции активации вершины. Обозначим выход -той вершины слоя как .

,

где — параметры функции активации -той вершины слоя .

Обучение методом обратного распространения ошибки в такой сети связано с настройкой параметров сети ( ) таким образом, чтобы ошибка на выходе была минимальной.

Предположим, что имеются P обучающих пар. Для входной обучающей пары p (p = 1,2,…,P) определим меру ошибки следующим образом:

, (2.23)

где

есть k-ая компонента вектора желаемого выхода для входного вектора p,

— k-ая компонента вектора реального выхода для входного вектора p, — число выходных вершин.

Введем сигнал ошибки, связанной с выходом -той вершиной слоя, как производную от меры ошибки:

Сигнал ошибки, связанной с выходом -той вершиной выходного слоя L, вычисляется как

Используя (2.23), имеем:

.

Сигнал ошибки, связанной с выходом -той вершины промежуточного слоя, зависит от сигнала ошибки (l+1) слоя и от производной функции активации нейронов слоя (l +1). Таким образом, сигнал ошибки может быть вычислен следующим образом:

(2.24)

Для процесса обучения, связанного с настройкой параметров сети, также будем использовать градиентный метод. Определим градиентный вектор как производную меры ошибки от параметров. Если — параметр функции активации -той вершины слоя, то, используя (2.24), то можем представить градиент ошибки по отношению к данному параметру как:

(2.25)

Далее, суммируя по всем обучающим парам, получим суммарную величину градиентов ошибки:

.

Теперь можем написать следующее правило обновления (обучения) параметров сети: на каждой следующей итерации алгоритма обучения добавлять к параметру его поправку в виде:

,

где 0 < η < 1 — множитель, задающий скорость обучения.