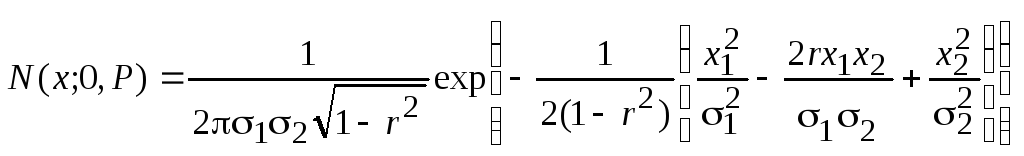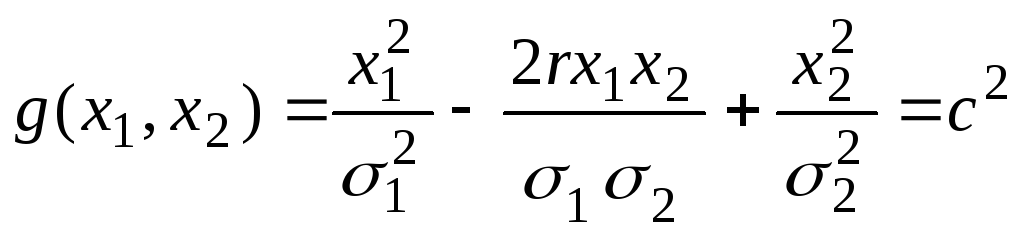Вероятная круговая ошибка

From Wikipedia, the free encyclopedia

CEP concept and hit probability. 0.2% outside the outmost circle.

In the military science of ballistics, circular error probable (CEP)^[1] (also circular error probability^[2] or circle of equal probability^[3]) is a measure of a weapon system’s precision. It is defined as the radius of a circle, centered on the mean, whose perimeter is expected to include the landing points of 50% of the rounds; said otherwise, it is the median error radius.^[4]^[5] That is, if a given munitions design has a CEP of 100 m, when 100 munitions are targeted at the same point, 50 will fall within a circle with a radius of 100 m around their average impact point. (The distance between the target point and the average impact point is referred to as bias.)

There are associated concepts, such as the DRMS (distance root mean square), which is the square root of the average squared distance error, and R95, which is the radius of the circle where 95% of the values would fall in.

The concept of CEP also plays a role when measuring the accuracy of a position obtained by a navigation system, such as GPS or older systems such as LORAN and Loran-C.

Concept[edit]

20 hits distribution example

The original concept of CEP was based on a circular bivariate normal distribution (CBN) with CEP as a parameter of the CBN just as μ and σ are parameters of the normal distribution. Munitions with this distribution behavior tend to cluster around the mean impact point, with most reasonably close, progressively fewer and fewer further away, and very few at long distance. That is, if CEP is n metres, 50% of shots land within n metres of the mean impact, 43.7% between n and 2n, and 6.1% between 2n and 3n metres, and the proportion of shots that land farther than three times the CEP from the mean is only 0.2%.

CEP is not a good measure of accuracy when this distribution behavior is not met. Precision-guided munitions generally have more «close misses» and so are not normally distributed. Munitions may also have larger standard deviation of range errors than the standard deviation of azimuth (deflection) errors, resulting in an elliptical confidence region. Munition samples may not be exactly on target, that is, the mean vector will not be (0,0). This is referred to as bias.

To incorporate accuracy into the CEP concept in these conditions, CEP can be defined as the square root of the mean square error (MSE). The MSE will be the sum of the variance of the range error plus the variance of the azimuth error plus the covariance of the range error with the azimuth error plus the square of the bias. Thus the MSE results from pooling all these sources of error, geometrically corresponding to radius of a circle within which 50% of rounds will land.

Several methods have been introduced to estimate CEP from shot data. Included in these methods are the plug-in approach of Blischke and Halpin (1966), the Bayesian approach of Spall and Maryak (1992), and the maximum likelihood approach of Winkler and Bickert (2012). The Spall and Maryak approach applies when the shot data represent a mixture of different projectile characteristics (e.g., shots from multiple munitions types or from multiple locations directed at one target).

Conversion[edit]

While 50% is a very common definition for CEP, the circle dimension can be defined for percentages. Percentiles can be determined by recognizing that the horizontal position error is defined by a 2D vector which components are two orthogonal Gaussian random variables (one for each axis), assumed uncorrelated, each having a standard deviation sigma . The distance error is the magnitude of that vector; it is a property of 2D Gaussian vectors that the magnitude follows the Rayleigh distribution, with a standard deviation ${displaystyle sigma _{d}={sqrt {2}}sigma }$ , called the distance root mean square (DRMS). In turn, the properties of the Rayleigh distribution are that its percentile at level is given by the following formula:

{displaystyle Q(F,sigma )=sigma {sqrt {-2ln(1-F/100%)}}}

or, expressed in terms of the DRMS:

${displaystyle Q(F,sigma _{d})=sigma _{d}{frac {sqrt {-2ln(1-F/100%)}}{sqrt {2}}}}$

The relation between and are given by the following table, where the values for DRMS and 2DRMS (twice the distance root mean square) are specific to the Rayleigh distribution and are found numerically, while the CEP, R95 (95% radius) and R99.7 (99.7% radius) values are defined based on the 68–95–99.7 rule

Measure of	Probability
DRMS	63.213…
CEP	50
2DRMS	98.169…
R95	95
R99.7	99.7

We can then derive a conversion table to convert values expressed for one percentile level, to another.^[6]^[7] Said conversion table, giving the coefficients alpha to convert into , is given by:

From to	RMS ()	CEP	DRMS	R95	2DRMS	R99.7
RMS ()	1.00	1.18	1.41	2.45	2.83	3.41
CEP	0.849	1.00	1.20	2.08	2.40	2.90
DRMS	0.707	0.833	1.00	1.73	2.00	2.41
R95	0.409	0.481	0.578	1.00	1.16	1.39
2DRMS	0.354	0.416	0.500	0.865	1.00	1.21
R99.7	0.293	0.345	0.415	0.718	0.830	1.00

For example, a GPS receiver having a 1.25 m DRMS will have a 1.25 m × 1.73 = 2.16 m 95% radius.

Warning: often, sensor datasheets or other publications state «RMS» values which in general, but not always,^[8] stand for «DRMS» values. Also, be wary of habits coming from properties of a 1D normal distribution, such as the 68-95-99.7 rule, in essence trying to say that «R95 = 2DRMS». As shown above, these properties simply do not translate to the distance errors. Finally, mind that these values are obtained for a theoretical distribution; while generally being true for real data, these may be affected by other effects, which the model does not represent.

References[edit]

^ Circular Error Probable (CEP), Air Force Operational Test and Evaluation Center Technical Paper 6, Ver 2, July 1987, p. 1
^ Nelson, William (1988). «Use of Circular Error Probability in Target Detection». Bedford, MA: The MITRE Corporation; United States Air Force. Archived (PDF) from the original on October 28, 2014.
^ Ehrlich, Robert (1985). Waging Nuclear Peace: The Technology and Politics of Nuclear Weapons. Albany, NY: State University of New York Press. p. 63.
^ Circular Error Probable (CEP), Air Force Operational Test and Evaluation Center Technical Paper 6, ver. 2, July 1987, p. 1
^ Payne, Craig, ed. (2006). Principles of Naval Weapon Systems. Annapolis, MD: Naval Institute Press. p. 342.
^ Frank van Diggelen, «GPS Accuracy: Lies, Damn Lies, and Statistics», GPS World, Vol 9 No. 1, January 1998
^ Frank van Diggelen, «GNSS Accuracy – Lies, Damn Lies and Statistics», GPS World, Vol 18 No. 1, January 2007. Sequel to previous article with similar title [1] [2]
^ For instance, the International Hydrographic Organization, in the IHO standard for hydrographic survey S-44 (fifth edition) defines «the 95% confidence level for 2D quantities (e.g. position) is defined as 2.45 × standard deviation», which is true only if we are speaking about the standard deviation of the underlying 1D variable, defined as above.

External links[edit]

Circular Error Probable in Ballistipedia

Источник

Среднеквадратический эллипс ошибок, круговая вероятная ошибка

Проанализируем
более подробно характеристики,
используемые для описания свойств
двухмерных гауссовских векторов.
Двухмерный случай весьма важен в задачах
обработки статистической информации.
Так, при решении навигационных задач
на плоскости нередко полагают, что
координаты объекта представляют собой
гауссовский случайный вектор с
математическим ожиданием в точке его
предполагаемого местонахождения. Для
описания неопределенности расположения
точки на плоскости используют введенные
выше эллипсы равных вероятностей, в
частности эллипс, соответствующий
уравнению (3.35) при
.
Поскольку этот эллипс пересекает оси
в точках, совпадающих со значениями
соответствующих СКО, т.е. при,
а при,
он получил наименованиесреднеквадратического
эллипса ошибок, или стандартного эллипса
[23]. В
навигационных приложениях для его
описания используют параметры
эллипса:
большую
ималую
полуоси
и дирекционный
угол
,
задающий ориентацию большой полуоси
относительно оси.
Эти три параметра полностью определяют
матрицу ковариаций двухмерной гауссовской
плотности. На рис. 3.4 изображен частный
случай, когда,
,
,
и таким
образом

, (3.36)

т.е. размеры полуосей
эллипса определяют значения СКО по
каждой координате.

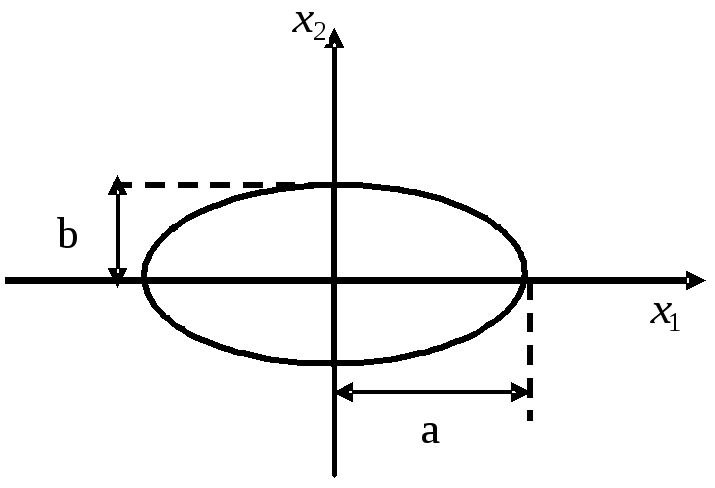
Рис.
1.2.4. Эллипс ошибок для двухмерного
гауссовского вектора

с независимыми
компонентами

При оценивании
точности местоположения подвижных
объектов весьма важным представляется
умение охарактеризовать неопределенность
местоположения одним
числом. Для
этих целей обычно используют значения
вероятности
попадания
точки на плоскости в ту или иную заданную
область
.
Для двухмерного центрированного
гауссовского вектора с плотностью

эта вероятность
определяется как

, (3.37)

Если в качестве
выступает область, ограниченная

то, переходя к
полярным координатам, можно показать,
что [44, с. 68]

. (3.38)

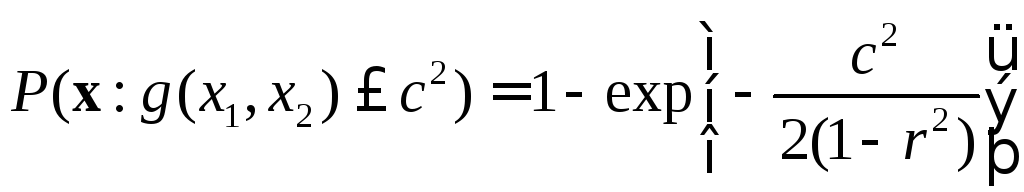
Для случая
независимых случайных величин при
эллипс превращается в окружность
радиусоми, таким образом, из (3.38) получаем, что
вероятность нахождения случайного
вектора в круге с таким радиусом
определяется введенным в разделе 2
распределением Рэлея

,
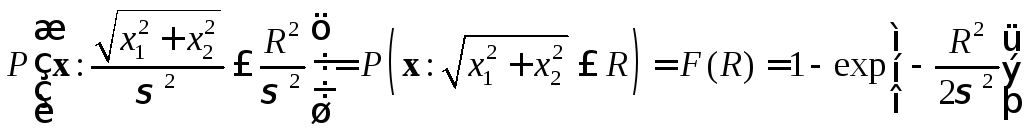
R>0. (1.39)

Круговая вероятная
ошибка (КВО).
Величина
,
соответствующая 50-процентному попаданию
гауссовского случайного вектора в круг
заданного радиуса, т.е. когда вероятность
попадания равна 0,5, называетсякруговой
вероятной ошибкой (КВО),
а круг, соответственно, кругом
равных вероятностей.
В англоязычной литературе для круговой
вероятной ошибки используется термин
circular error
probable (CEP).

Отметим, что для
независимых
случайных величин с равными
СКО

,
50-процентное попадание в круг (P=0,5)
достигается при
1,177.
Для круга радиуса
обеспечивается попадание с вероятностьюP=0,997.
В случае если
радиус круга, при котором достигается
вероятность попадания в него, равная
0,5, либо другой вероятности следует
отыскивать с помощью соотношения (3.37).

Радиальная
среднеквадратическая ошибка (Distance
Root Mean Square (DRMS)

Эта ошибка
определяется как

. (3.40)

Отметим, что
вероятность попадания в круг такого
радиуса составляет величину 0.65-0.68 в
зависимости от значений параметров
эллипса рассеивания.

Удвоенная
радиальная среднеквадратическая ошибка
(2DRMS).

Вероятность
попадания в круг такого удвоенного
радиуса зависит от конкретных соотношений
СКО и коэффициента корреляции, а примерная
ее величина определяется как P=0,95.

Понятия, аналогичные
приведенным выше, используются и для
трехмерного гауссовского вектора. При
этом вводится величина сферической
вероятной ошибки (СВО)
и сферы равных
вероятностей
(spherical error
probable (SEP)
и sphere of equal
probability (SEP)). Трехмерное
гауссовское распределение широко
используется при описании ошибок
местоположения подвижных объектов в
пространстве, в частности для летательных
аппаратов.

Соседние файлы в папке Кафедра ТВ

Источник

Похожие статьи см . в CEP .

Вероятность круговой ошибки ( CEP ) при x% — это радиус круга, внутри которого лежат x% значений двумерной выборки измерений. Этот процент отмечается как индекс (например, CEP при 20%: ). Это индикатор, обычно используемый для определения точности военных баллистических выстрелов или для определения местоположения по GPS.

Если вероятность не указана, дается вероятное круговое отклонение (CPE) на уровне 50%. Этот термин в основном используется для выражения характеристики точности ракеты или снаряда, обычно ракеты большой дальности класса «земля-поверхность », « воздух-поверхность » или « море-поверхность », используемой в качестве фактора для определения вероятной эффективности. ракеты оружие на своей цели. Определение из AAP-21 , глоссария терминов и определений ядерного , радиологического, бактериологического и химического оружия НАТО , таково: Вероятное круговое отклонение определяется как радиус круга, в пределах которого упадет 50 процентов снарядов или ракет ^{[ 1 ]} .

Например, GPS -позиционирование в сочетании с системой EGNOS обеспечивает точность CEP 3 м . Это означает, что погрешность между измеренным положением и фактическим положением составляет менее 3 м в 50% случаев.

Если двумерный случайный вектор , компоненты которого независимы, подчиняется центрированному нормальному распределению , где матрица дисперсии-ковариации, можно определить CEP в общем виде по следующей формуле:

где – вероятность того, что случайная величина примет значение внутри круга радиуса .

Вероятность того, что случайная величина примет значение внутри круга радиуса 2CEP, составляет 93,8 %, а для радиуса 3CEP — 99,8 %.

В случае двумерного центрированного нормального распределения с двумя дисперсиями, равными , мы имеем следующее соотношение:

Затем CEP рассчитывается в соответствии с дисперсией :

Примечания и ссылки

↑ [ PDF] НАТО/РОССИЯ БЕЗ СЕССИИ , стр. 6

Источник

1
circular error probable

CEP, circular error probable

————————

CIREP, circular error probable

English-Russian dictionary of planing, cross-planing and slotting machines > circular error probable
2
circular error probable
1. круговая вероятная ошибка
круговая вероятная ошибка
Радиус круга в точке определения местоположения, внутри которого истинное положение объекта находится с вероятностью 50 %. Ср. spherical error probable.
[Л.М. Невдяев. Телекоммуникационные технологии. Англо-русский толковый словарь-справочник. Под редакцией Ю.М. Горностаева. Москва, 2002]

Тематики
- электросвязь, основные понятия
EN
- circular error probable
- СЕР
Англо-русский словарь нормативно-технической терминологии > circular error probable
3
circular error probable

Универсальный англо-русский словарь > circular error probable
4
circular error probable

Англо-русский дипломатический словарь > circular error probable
5
circular error probable

English-Russian military dictionary > circular error probable
6
circular error probable

English-Russian dictionary on nuclear export control > circular error probable
7
circular error probable

круговое вероятное отклонение; КВО

English-Russian small dictionary of medicine > circular error probable
8
circular error probable buffer distance

Универсальный англо-русский словарь > circular error probable buffer distance
9
circular error probable/probability

Универсальный англо-русский словарь > circular error probable/probability
10
circular error probable buffer distance

дополнительное расстояние с учетом срединного [вероятного] отклонения

English-Russian military dictionary > circular error probable buffer distance
11
CEP — circular error probable

КВО — круговая вероятная ошибка

Терминологический словарь МИД России > CEP — circular error probable
12
probable circular error

PCE, probable circular error

вероятная круговая ошибка [отклонение], срединное отклонение

English-Russian dictionary of planing, cross-planing and slotting machines > probable circular error
13
probable circular error

Универсальный англо-русский словарь > probable circular error
14
error

ошибка, погрешность; дефект; расхождение, рассогласование

— biased error

English-Russian military dictionary > error
15
error

ошибка, погрешность; отклонение; рассогласование

static pressure port error — погрешность, обусловленная расположением и формой отверстия для приёма статического давления

Englsh-Russian aviation and space dictionary > error
16
error

English-Russian electronics dictionary > error
17
error

The New English-Russian Dictionary of Radio-electronics > error
18
circular probable error

CPE, circular probable error

English-Russian dictionary of planing, cross-planing and slotting machines > circular probable error
19
probable

English-Russian big polytechnic dictionary > probable
20
circular probable error

Универсальный англо-русский словарь > circular probable error

Страницы

См. также в других словарях:

Circular error probable — In the military science of ballistics, circular error probable (CEP) (also circular error probability or circle of equal probability[1]) is an intuitive measure of a weapon system s precision. It is defined as the radius of a circle, centered… … Wikipedia
Circular Error Probable — Der Circular Error Probable (kurz CEP, auf deutsch: Kreisfehlerwahrscheinlichkeit oder Streukreisradius) gibt bei einer kreisförmigen Normalverteilung den Radius eines Kreises an, in dem 50 Prozent aller Messwerte liegen. Der CEP dient als ein… … Deutsch Wikipedia
circular error probable — apskritiminės paklaidos tikimybė statusas T sritis Gynyba apibrėžtis Raketos (sviedinio) pataikymo tikslumo rodiklis, naudojamas kaip veiksnys nustatant tikimą žalą taikiniui. Tai yra apskritimo, į kurį tikimasi, kad bus pataikyta pusė raketų… … NATO terminų aiškinamasis žodynas
circular error probable — apskritimo paklaidos tikimybė statusas T sritis Gynyba apibrėžtis Raketos (sviedinio) pataikymo rodiklis, pagal kurį nustatoma tikima žala taikiniui. Tai yra apskritimo, į kurį tikimasi, kad pataikys pusė raketų (sviedinių), spindulys.… … Artilerijos terminų žodynas
circular error probable — An indicator of the delivery accuracy of a weapon system, used as a factor in determining probable damage to a target. It is the radius of a circle within which half of a missile … Military dictionary
circular error probability — The radius of a circle within which half the missiles or projectiles are expected to fall. It is an indicator of the delivery accuracy of a weapon system, used as a factor in determining probable damage to a target. The CEP is expressed as a… … Aviation dictionary
Circular — is a basic geometric shape such as a Circle. Contents 1 Documents 2 Travel and transportation 3 Places … Wikipedia
horizontal error — The error in range, deflection, or in radius, which a weapon may be expected to exceed as often as not. Horizontal error of weapons making a nearly vertical approach to the target is described in terms of circular error probable. Horizontal error … Military dictionary
Erreur Circulaire Probable — L Erreur circulaire probable (Circular Error Probable, CEP) à x % est le rayon du cercle à l intérieur duquel se trouvent x % des valeurs d un échantillon de mesure bidimensionnelle. On note ce pourcentage en indice (par exemple, CEP à… … Wikipédia en Français
delivery error — The inaccuracy associated with a given weapon system resulting in a dispersion of shots about the aiming point. See also circular error probable; deviation; dispersion; dispersion error; horizontal error … Military dictionary
écart circulaire probable — apskritiminės paklaidos tikimybė statusas T sritis Gynyba apibrėžtis Raketos (sviedinio) pataikymo tikslumo rodiklis, naudojamas kaip veiksnys nustatant tikimą žalą taikiniui. Tai yra apskritimo, į kurį tikimasi, kad bus pataikyta pusė raketų… … NATO terminų aiškinamasis žodynas

Источник

Круглая вероятная ошибка

В военной науке о баллистике круглая вероятная ошибка (CEP) (также круглая ошибочная вероятность или круг равной вероятности) является мерой точности системы оружия. Это определено как радиус круга, сосредоточенного о среднем, граница которого, как ожидают, будет включать приземляющиеся пункты 50% раундов.

Понятие

Оригинальное понятие БЕЛОГО ГРИБА было основано на круглом двумерном нормальном распределении (CBN) с БЕЛЫМ ГРИБОМ как параметр CBN так же, как μ, и σ — параметры нормального распределения. Боеприпасы с этим поведением распределения имеют тенденцию группироваться вокруг пункта цели, с наиболее довольно близким, прогрессивно меньше и меньше еще дальше и очень немногие на большом расстоянии. Таким образом, если БЕЛЫЙ ГРИБ — n метры, 50% земли раундов в пределах n метров цели, 43% между n и 2n, и 7% между 2n и 3n, метры и пропорция раундов, которые приземляются дальше, чем три раза БЕЛЫЙ ГРИБ от цели, составляют меньше чем 0,2%.

Это поведение распределения часто не встречается. Управляемые точностью боеприпасы обычно имеют больше «близких промахов» и так обычно не распределяются. У боеприпасов может также быть большее стандартное отклонение ошибок диапазона, чем стандартное отклонение азимута (отклонение) ошибки, приводящие к эллиптической области уверенности. Образцы снаряжения могут не быть точно на цели, то есть, средний вектор не будет (0,0). Это упоминается как уклон.

Чтобы применить понятие БЕЛОГО ГРИБА в этих условиях, БЕЛЫЙ ГРИБ может быть определен как квадратный корень среднеквадратической ошибки (MSE). MSE будет суммой различия ошибки диапазона плюс различие ошибки азимута плюс ковариация ошибки диапазона с ошибкой азимута плюс квадрат уклона. Таким образом следствия MSE объединения всех этих источников ошибки, геометрически соответствуя радиусу круга, в пределах которого приземлятся 50% раундов.

Преобразование между БЕЛЫМ ГРИБОМ, RMS, 2DRMS, и R95

В то время как 50% — очень общее определение для БЕЛОГО ГРИБА, измерение круга может быть определено для процентов. Приблизительные формулы доступны, чтобы преобразовать распределения вдоль этих двух топоров в эквивалентный радиус круга для указанного процента.

Дополнительные материалы для чтения

Источник

Вероятная круговая ошибка

Concept[edit]

Conversion[edit]

See also[edit]

References[edit]

Further reading[edit]

External links[edit]

Среднеквадратический эллипс ошибок, круговая вероятная ошибка