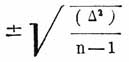Все наши наблюдения и опытные исследования подвержены большим или меньшим ошибкам, причина которых заключается частью в несовершенстве наших чувств, частью в несовершенстве употребляемых нами инструментов. Ошибки эти делятся на постоянные (систематические) и случайные; постоянной ошибкой называется такая, которая при всех измерениях какой-либо величины или остается постоянной, или ее изменения следуют какому-либо определенному закону; случайной же называется ошибка, появляющаяся без определенного порядка и происходящая то в одну, то в другую сторону. Чтобы ослабить влияние случайных ошибок на результат, одни и те же наблюдения повторяют несколько раз, так что для наблюдаемой величины получается несколько более или менее отличных друг от друга результатов. Наиболее правдоподобным или невероятнейшим значением определяемой величины, если все отдельные наблюдения равно благонадежны, считается среднее арифметическое из отдельных результатов. Разности между средним арифметическим и результатами каждого отдельного наблюдения принимаются за случайные ошибки (при этом предполагается, конечно, что влияние постоянных ошибок уже принято во внимание). Представим себе теперь, что имеется ряд измерений какой-нибудь величины и, следовательно, соответствующий этим измерениям ряд ошибок; та ошибка, численная величина которой такова, что число всех ошибок, меньших ее, равно числу ошибок, больших ее, называется, следуя Гауссу, вероятною (erreur moyenne à craindre); она дает возможность судить о достоинстве измерения какой-либо величины. Астрономы и геодезисты, измерения которых отличаются чрезвычайною точностью, сообщая результаты своих измерений, приводят обыкновенно и вероятную ошибку их. Вместо вероятной ошибки иногда дается средняя; средней называется такая ошибка, квадрат которой равен среднему арифметическому из квадратов всех ошибок рассматриваемого ряда наблюдений. В простейшем случае, когда для определения искомой величины произведен достаточно многочисленный ряд равно благонадежных измерений, средняя ошибка отдельного измерения вычисляется по формуле
а средняя ошибка результата (среднего арифметического) по формуле
где (Δ2) означает сумму квадратов всех уклонений отдельных измерений от среднего арифметического, а n — число измерений. Вероятная ошибка приблизительно в полтора раза менее средней. Величину вероятной ошибки можно найти еще следующим, хотя и грубым, способом, вытекающим из самого ее определения: из всего числа ошибок отобрать по порядку половину их, по численной величине наиболее близких к нулю; тогда ошибка, находящаяся на границе отобранных с остальными, и будет приблизительно равна В. ошибке отдельного измерения. В более общем случае, когда различные, не зависимые друг от друга выводы для искомой величины неодинаково благонадежны, при вычислении вероятнейшего значения искомой величины, а также вероятной и средней ошибки ее, принимают в расчет так наз. веса выводов; относительным весом наз. число, обратно пропорциональное квадрату средней ошибки разных выводов, причем единица веса произвольна.
См. Gauss, «Theoria combinationis observationum erroribus minimis obnoxiae» (1821); Буняковский, «Теория вероятностей»; Савич, «Приложение теории вероятностей к вычислению наблюдений etc.».
А. Жданов.
Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона. — С.-Пб.: Брокгауз-Ефрон.
1890—1907.
From Wikipedia, the free encyclopedia
In statistics, probable error defines the half-range of an interval about a central point for the distribution, such that half of the values from the distribution will lie within the interval and half outside.[1]
Thus for a symmetric distribution it is equivalent to half the interquartile range, or the median absolute deviation. One such use of the term probable error in this sense is as the name for the scale parameter of the Cauchy distribution, which does not have a standard deviation.
The probable error can also be expressed as a multiple of the standard deviation σ,[1][2] which requires that at least the second statistical moment of the distribution should exist, whereas the other definition does not. For a normal distribution this is

See also[edit]
- Average absolute deviation
- Circular error probable
- Confidence interval
- Standard error
References[edit]
- ^ a b Dodge, Y. (2006) The Oxford Dictionary of Statistical Terms, OUP. ISBN 0-19-920613-9
- ^ Zwillinger, D.; Kokosa, S. (2000) CRC Standard Probability and Statistics Tables and Formulae, Chapman & Hall/CRC. ISBN 1584880597 (Section 2.2.13)
Значение слова «ВЕРОЯТНАЯ ОШИБКА» найдено в 18 источниках
ВЕРОЯТНАЯ ОШИБКА
Все наши наблюдения и опытные исследования подвержены большим или меньшим ошибкам, причина которых заключается частью в несовершенстве наших чувств, частью в несовершенстве употребляемых нами инструментов. Ошибки эти делятся на постоянные (систематические) и случайные; постоянной ошибкой называется такая, которая при всех измерениях какой-либо величины или остается постоянной, или ее изменения следуют какому-либо определенному закону; случайной же называется ошибка, появляющаяся без определенного порядка и происходящая то в одну, то в другую сторону. Чтобы ослабить влияние случайных ошибок на результат, одни и те же наблюдения повторяют несколько раз, так что для наблюдаемой величины получается несколько более или менее отличных друг от друга результатов.Наиболее правдоподобным или невероятнейшим значением определяемой величины, если все отдельные наблюдения равно благонадежны, считается среднее арифметическое из отдельных результатов. Разности между средним арифметическим и результатами каждого отдельного наблюдения принимаются за случайные ошибки (при этом предполагается, конечно, что влияние постоянных ошибок уже принято во внимание). Представим себе теперь, что имеется ряд измерений какой-нибудь величины и, следовательно, соответствующий этим измерениям ряд ошибок; та ошибка, численная величина которой такова, что число всех ошибок, меньших ее, равно числу ошибок, больших ее, называется, следуя Гауссу, вероятною (erreur moyenne à craindre); она дает возможность судить о достоинстве измерения какой-либо величины. Астрономы и геодезисты, измерения которых отличаются чрезвычайною точностью, сообщая результаты своих измерений, приводят обыкновенно и вероятную ошибку их. Вместо вероятной ошибки иногда дается средняя; средней называется такая ошибка, квадрат которой равен среднему арифметическому из квадратов всех ошибок рассматриваемого ряда наблюдений. В простейшем случае, когда для определения искомой величины произведен достаточно многочисленный ряд равно благонадежных измерений, средняя ошибка отдельного измерения вычисляется по формуле
а средняя ошибка результата (среднего арифметического) по формуле
где (Δ2) означает сумму квадратов всех уклонений отдельных измерений от среднего арифметического, а n — число измерений. Вероятная ошибка приблизительно в полтора раза менее средней. Величину вероятной ошибки можно найти еще следующим, хотя и грубым, способом, вытекающим из самого ее определения: из всего числа ошибок отобрать по порядку половину их, по численной величине наиболее близких к нулю; тогда ошибка, находящаяся на границе отобранных с остальными, и будет приблизительно равна В. ошибке отдельного измерения. В более общем случае, когда различные, не зависимые друг от друга выводы для искомой величины неодинаково благонадежны, при вычислении вероятнейшего значения искомой величины, а также вероятной и средней ошибки ее, принимают в расчет так наз. веса выводов; относительным весом наз. число, обратно пропорциональное квадрату средней ошибки разных выводов, причем единица веса произвольна.
См. Gauss, «Theoria combinationis observationum erroribus minimis obnoxiae» (1821); Буняковский, «Теория вероятностей»; Савич, «Приложение теории вероятностей к вычислению наблюдений etc.».
А. Жданов.
Найдено 2 изображения:
Изображения из описаний на этой странице
Вероятная ошибка — Bсе наши наблюдения и опытные исследования подвержены большим или меньшим ошибкам, причина которых заключается частью в несовершенстве наших чувств, частью в несовершенстве употребляемых нами инструментов. Ошибки эти делятся на постоянные (систематические) и случайные; постоянной ошибкой называется такая, которая при всех измерениях какой-либо величины или остается постоянной, или ее изменения следуют какому-либо определенному закону; случайной же называется ошибка, появляющаяся без определенного порядка и происходящая то в одну, то в другую сторону. Чтобы ослабить влияние случайных ошибок на результат, одни и те же наблюдения повторяют несколько раз, так что для наблюдаемой величины получается несколько болee или менее отличных друг от друга результатов. Наиболее правдоподобным или невероятнейшим значением определяемой величины, если все отдельные наблюдения равно благонадежны, считается среднее арифметическое из отдельных результатов. Разности между средним арифметическим и результатами каждого отдельного наблюдения принимаются за случайные ошибки (при этом предполагается, конечно, что влияние постоянных ошибок уже принято во внимание). Представим себе теперь, что имеется ряд измерений какой-нибудь величины и, следовательно, соответствующий этим измерениям ряд ошибок; та ошибка, численная величина которой такова, что число всех ошибок, меньших ее, равно числу ошибок, больших ее, называется, следуя Гауссу, вероятною (erreur moyenne à craindre); о на дает возможность судить о достоинстве измерения какой-либо величины. Астрономы и геодезисты, измерения которых отличаются чрезвычайною точностью, сообщая результаты своих измерений, приводят обыкновенно и вероятную ошибку их. Вместо вероятной ошибки иногда дается средняя; средней называется такая ошибка, квадрат которой равен среднему арифметическому из квадратов всех ошибок рассматриваемого ряда наблюдений. В простейшем случае, когда для определения искомой величины произведен достаточно многочисленный ряд равно благонадежных измерений, средняя ошибка отдельного измерения вычисляется по формуле а средняя ошибка результата (среднего арифметического) по формуле где (Δ 2) означает сумму квадратов всех уклонений отдельных измерений от среднего арифметического, а n — число измерений. Вероятная ошибка приблизительно в полтора раза менее средней. Величину вероятной ошибки можно найти еще следующим, хотя и грубым, способом, вытекающим из самого ее определения: из всего числа ошибок отобрать по порядку половину их, по численной величине наиболее близких к нулю; тогда ошибка, находящаяся на границе отобранных с остальными, и будет приблизительно равна В. ошибке отдельного измерения. В более общем случае, когда различные, не зависимые друг от друга выводы для искомой величины неодинаково благонадежны, при вычислении вероятнейшего значения искомой величины, а также вероятной и средней ошибки ее, принимают в расчет так наз. веса выводов; относительным весом наз. число, обратно пропорциональное квадрату средней ошибки разных выводов, причем единица веса произвольна. См. Gauss, «Theoria combinationis observationum erroribus minimis obnoxiae» (1821); Буняковский, «Теория вероятностей»; Савич, «Приложение теории вероятностей к вычислению наблюдений etc.». А. Жданов.
probable error
* * *
probable error
Средняя ошибка
полученная как среднеарифметическое
из истинных ошибок, дает неверное
представление о точности результатов,
так как при сложении положительных и
отрицательных ошибок компенсируется.
Поэтому определяют среднее арифметическое
из абсолютных значений ошибок.
v=[|∆|]/n,
где ∆-среднеарифметическое, n-число
измерений.
В таком случае
средняя ошибка наиболее достоверна, но
средняя ошибка недостаточно точно
характеризует результаты измерений,
т.к сглаживает влияние больших по
величине ошибок.
Чтобы усилить их
влияние нужно их возвести в квадрат и
получают средние
квадратические ошибки.
m=√([∆2]/n)
Преимущество СКО
по сравнению со средними:
1.Учитывают влияние
больших по величине ошибок.
2.СКО одного измерения
(me)
определенная из небольшого числа
измерений мало отличается от СКО большого
числа таких же измерений.
При оценке точности
результатов измерений достаточно чтобы
в оценке участвовали 4 рез-та, которые
дадут однозначное значение ошибки.
При оценке точности
после определения СКО необходимо
вычислить ошибку самой ошибки (надежность
ошибки):
mml=ml/√2n
Зная СКО можно
установить предельную ошибку, абсолютное
значение которой является верхней
границей допустимых при данных условиях
измерений размеров ошибок. ∆пр=ґm,
где ґ=2;2,5;3. Предельная ошибка устанавливается
инструкциями на все виды работ и
называется служебный
допуск.
Вероятная ошибка
— такое значение случайной ошибки при
данных условиях измерения по отношению
к которой ошибки и большие и меньшие по
абсолютной величине встречаются
одинаково часто. В теории вероятности
доказано, что при достаточно большом
числе измерений существуют следующие
зависимости: вероятная ошибка составляет
2/3 квадратической ошибки, а средняя
ошибка составляет 4/5 от средней
квадратической ошибки.
r=2/3m;
v=4/5m.
Истинная, средняя,
вероятная, СКО, предельные ошибки
называются абсолютными.
В тех случаях
когда на точность измерений влияет
размер определяемой величины, то оценка
точности по абсолютной ошибке становится
недостаточной и судить о качестве
измерений нельзя.
Во всех таких
случаях для точности применяют понятие
относительная
ошибка —
отвлеченное число выражающее отношение
абсолютной ошибка измерения к его
результату.
13. Математическая обработка равноточных измерений. Арифметическое среднее, ско арифметической середины.
1.Имеется
ряд равноточных измерений l1,l2…,ln.
За окончательное значение принимаем
среднее из них.
L=(l1+l2+…+ln)/n=[l]/n.
Сравним каждый
результат с точным значением x
и получим ряд истинных ошибок.
∆1=l1-x
∆2=l2-x
…..
∆n=ln-x
где х — точное
значение измеренной величины.
Сложим все и получим
[∆]=[l]-nx.
Выразим отсюда
величину точного значения
x=[l]/n-[∆]/n.
При бесконечном
числе измерений среднее арифметическое
значение их находится ближе всего к
точному их значению х, чем любой из
результатов измерений (l1,l2…ln)
поэтому его называть вероятнейшим
значением измеренной величины.
2.
Если X-точное
значение измеренной величины, а L
-вероятнейшее значение, то М-ошибка
арифметического среднего или вероятнейшее
значение измереной величины.
М= L-x;
Для вывода формулы
определим зависимость между ошибками.
Воспользуемся рядом истинных ошибок:
∆1=l1-x
∆2=l2-x
…..
∆n=ln-x
Сложим равенства
и разделим на n(количество
измерений).
[∆]/n=([l]/n)-x
[∆]/n=L-x
M=[∆]/n
Возведем в квадрат:
M2=(∆12+∆22+…+∆n2+2∆1∆2+2∆1∆3+…+2∆1∆n+…+2∆2∆3+2∆2∆4+…+2∆2∆n+…+2∆n-1∆n)/n2
В числителе этой
формулы удвоенные произведения имеют
разные знаки и при возрастании числа
измерений сумма их стремится к 0 поэтому
отбросив их получим приближенные
равенства.
M2=(∆12+∆22+…+∆n2)/
n2
M2=[∆2]/n2
ml=√([∆2]/n)
M=ml/√n
mL=
ml/√n
– среднеквадратическая ошибка
вероятнейшего значения через СКО
Средняя ошибка
меньше СКО одного измерения.
14-15.Оценка точности
результатов равноточных измерений по
истинным ошибкам. Формулы, порядок
вычислений.
Случайные ошибки
в ряду измерений отличаются одна от
другой на незначительную величину. О
точности измерений можно судить по
значению средней ошибки.
Средняя ошибка,
полученная как среднее арифметическое
из истинных ошибок, дает неверное
представление о точности результатов,
так как при сложении положительных и
отрицательных ошибок компенсируется.
Поэтому определяют среднее арифметическое
из абсолютных значений ошибок.
v=[|∆|]/n,
где ∆-среднеарифметическое, n-число
измерений.
В таком случае
средняя ошибка будет наиболее достоверна,
но средняя ошибка недостаточно точно
характеризует результаты измерений,
так как сглаживает влияние больших по
величине ошибок.
Чтобы усилить их
влияние, их нужно возвести в квадрат. И
получают средние
квадратические ошибки.
ml=√[∆2/n]
При оценке точности
результатов измерений достаточно, чтобы
в этой оценке участвовали всего лишь 4
результата, которые дадут однозначное
значение ошибки. При оценке точности
после после определения СКО необходимо
вычислить ошибку самой ошибки (надежность
ошибки):
mml=ml/√2n
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
14.02.20152.46 Mб6Э.doc
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Читать PDF
Методологические ошибки в психолого-педагогических исследованиях и публикациях
В статье рассматриваются выявленные в процессе изучения и анализа многочисленных публикаций (научных статей, методических рекомендаций, учебно-методических пособий, монографий), диссертаций и авторефе
Читать PDF
Типичные ошибки психолога-диагноста
Ануфриев А.Ф., Рыжкова А.Н.
С помощью метода компьютерного моделирования диагностических задач изучаются типичные ошибки психолога-диагноста. Предлагается их теоретически обоснованная классификация.
Читать PDF
Когнитивные ошибки и способы их исправления
Сханов Руслан Александрович, Макаров Антон Валерьевич
В статье рассматривается проблема ошибочных действий, а также выдвигаются гипотезы относительно возможности элиминации ошибок в когнитивной деятельности субъекта.
Читать PDF
Современный уровень преступности несовершеннолетних и ошибки семейного воспитания, приводящие к форм
Широбокова Татьяна Сергеевна
Обеспечение нормальных условий развития и воспитания это основная обязанность родителей.
Читать PDF
«Самосознание, возможно, является ошибкой эволюции»: Олдос Хаксли о топографии сознания
Головачева И. В.
Структура и работа сознания трудно поддается словесному выражению, взывая к необходимости метафорического и символического описания. Олдосу Хаксли это прекрасно удавалось.
Читать PDF
Ошибки в процессе научения при разных способах оценки эталона
Сханов Р.А., Ворожейкин И.В., Филиппова М.Г., Макаров А.В.
В статье описана процедура и результаты исследования, нацеленного на выявление феноменов научения, связанных с оценкой двумя независимыми способами одного и того же релевантного стимула.
Читать PDF
Ошибки невнимания в слепоте по невниманию
Кувалдина Мария Борисовна
Данная статья посвящена экспериментальному исследованию слепоты по невниманию, поддерживаемой динамически.
Читать PDF
Ошибки воспроизведения оценочных суждений при противоречивой обратной связи
Козлов Дмитрий Дмитриевич, Агафонов Андрей Юрьевич, Шалаева Наталья Юрьевна
Статья посвящена изучению условий возникновения ошибок воспроизведения оценочных суждений при наличии противоречивой обратной связи.
Читать PDF
Ошибки материнского воспитания как фактор затрудненного общения ребенка
Самохвалова Анна Геннадьевна, Котова Ирина Владимировна
В статье рассматриваются коммуникативные трудности детей дошкольного возраста, возникающие в процессе межличностного общения со взрослыми и сверстниками; влияние стилей и ошибок материнского воспитани
Читать PDF
Устойчивые ошибки в процессе научения: особенности и возможности прогнозирования
Андриянова Наталья Владимировна
В данной экспериментальной работе исследуется возможность прогнозирования устойчивых ошибок в процессе научения с помощью регистрации времени реакции и степени уверенности при ответе.
Читать PDF
Социальные страхи студентов: страх ошибки
Крутых Е.В.
В статье рассматривается страх ошибки у студентов. Указаны ситуации, в которых этот страх может проявляться. Исследование показало, что выраженный страх ошибки проявляется в основном у девушек.
Читать PDF
Ошибки в соревнованиях по портивному ориентированию как следствие отрицательных психических состояни
Казанцев Сергей Александрович, Федотова Анна Александровна, Федотов Юрий Николаевич