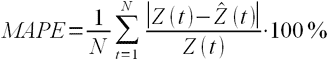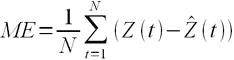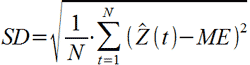Вероятная ошибка прогноза

Вариант 1

Задание 1. Модель парной линейной регрессии.

Имеются данные о размере среднемесячных доходов в разных группах семей

Задания:

1. Рассчитать линейный коэффициент парной корреляции, оценить его статистическую значимость и построить для него доверительный интервал с уровнем значимости a =0,05. Сделать выводы

2. Построить линейное уравнение парной регрессии Y на X и оценить статистическую значимость параметров регрессии. Сделать рисунок.

3. Оценить качество уравнения регрессии при помощи коэффициента детерминации. Сделать выводы. Проверить качество уравнения регрессии при помощи F-критерия Фишера.

4. Выполнить прогноз доли оплаты труда структуре доходов семьи Y при прогнозном значении среднедушевого денежного дохода X, составляющем 111% от среднего уровня. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал для уровня значимости a =0,05. Сделать выводы.

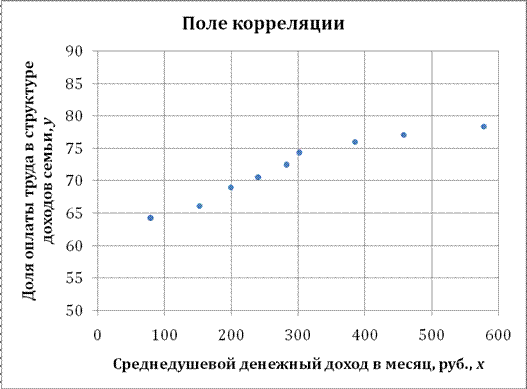
Решение: Построим поле корреляции зависимости доли оплаты труда в структуре доходов семьи от среднедушевого денежного дохода в месяц.

Точки на построенном графике размещаются вблизи кривой, напоминающей по форме Прямую, поэтому можно предположить, что между указанными величинами существует Линейная зависимость вида .

Для расчета линейного коэффициента парной корреляции и параметров линейной регрессии составим вспомогательную таблицу.

Вычислим коэффициент корреляции. Используем следующую формулу:

= 0,9568.

Можно сказать, что между рассматриваемыми признаками существует Прямая тесная Корреляционная связь.

Среднюю ошибку коэффициента корреляции определим по формуле:

= 0,032.

Найдем табличное значение TТабл по таблице распределения Стьюдента для
a = 0,05 и числе степеней свободы K = N – M – 1 = 9 – 1 – 1 = 7.

TТабл(0,05; 7) = 2,36.

Запишем доверительный интервал для коэффициента корреляции.

Доверительный интервал не включает число 0, поэтому при заданном уровне значимости коэффициент корреляции является статистически значимым.

Вычислим параметры уравнения регрессии.

= 0,03.

= 72,01 – 0,03×297,41 = 63,09.

Получим следующее уравнение: .

Для проверки статистической значимости (существенности) линейного коэффициента парной корреляции рассчитаем T-критерий Стьюдента по формуле:

= 23,04.

Фактическое значение по абсолютной величине больше табличного, что свидетельствует о значимости линейного коэффициента корреляции и существенности связи между рассматриваемыми признаками.

Проверим значимость оценок теоретических коэффициентов регрессии с помощью t-статистики Стьюдента и сделаем соответствующие выводы о значимости этих оценок.

Для определения статистической значимости коэффициентов A и B найдем T-статистики Стьюдента:

Рассчитаем по полученному уравнению теоретические значения. Составим вспомогательную таблицу.

Вычислим стандартные ошибки коэффициентов уравнения.

= 1,2.

= 0,003.

Вычислим T-статистики.

Сравнение расчетных и табличных величин критерия Стьюдента показывает, что и , т. е. оценки A и B теоретических коэффициентов регрессии статистически значимы.

Сделаем рисунок.

Рассчитаем коэффициент детерминации: = 0,95682= 0,915 = 91,5%.

Таким образом, вариация результата Y на 91,5% объясняется вариацией фактора X.

Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:

= 75,81.

Найдем табличное значение Fтабл по таблице критических точек Фишера для
a = 0,05; K1 = M = 1 (число факторов), K2 = N – M – 1 = 9 – 1 – 1 = 7.

Fтабл(0,05; 1; 7) = 5,59.

Поскольку F > FТабл, уравнение регрессии с вероятностью 0,95 в целом Является статистически значимым.

Выполним прогноз доли оплаты труда структуре доходов семьи y при прогнозном значении среднедушевого денежного дохода x, составляющем 111% от среднего уровня.

XP = 297,41 × 1,11 = 330,1.

Вычислим прогнозное значение Yp с помощью уравнения регрессии.

» 73%.

Доверительный интервал прогноза имеет вид

(УP – Tкр×My, УP + Tкр×My),

Где , M = 2 – число параметров уравнения.

= 1,695 » 1,7.

Запишем доверительный интервал прогноза:

Þ

Данный прогноз является надежным, поскольку доверительный интервал не включает число 0, точность прогноза составляет 4.

Задание 2. Модель парной нелинейной регрессии.

По территориям Центрального района известны данные за 1995 г.

Задания:

1. Построить поле корреляции и сформулируйте гипотезу о форме связи. Рассчитать параметры уравнений полулогарифмической () и степенной () парной регрессии. Сделать рисунки.

2. Дать с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом для каждой модели. Сделать выводы. Оценить качество уравнений регрессии с помощью средней ошибки аппроксимации и коэффициента детерминации. Сделать выводы.

3. По значениям рассчитанных характеристик выбрать лучшее уравнение регрессии. Дать экономический смысл коэффициентов выбранного уравнения регрессии

4. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости a =0,05. Сделать выводы.

Решение: Решение: Для предварительного определения вида связи между указанными признаками построим поле корреляции. Для этого построим в системе координат точки, у которых первая координата X, а вторая – Y.

Получим следующий рисунок.

По внешнему виду диаграммы рассеяния трудно предположить, какая зависимость существует между указанными показателями.

Построение полулогарифмической модели регрессии.

Уравнение логарифмической кривой: .

Обозначим:

Получим линейное уравнение регрессии:

Y = A + B×X.

Произведем линеаризацию модели путем замены . В результате получим линейное уравнение .

Рассчитаем его параметры, используя данные таблицы.

= -9,76.

= 225,6 – (-9,76)×5,26 = 276,99.

Уравнение модели имеет вид:

Определим индекс корреляции

Используя данные таблицы, получим:

.

Рассчитаем коэффициент детерминации: = 0,14642= 0,021 = 2,1%.

Вариация результата Y всего на 2,1% объясняется вариацией фактора X.

Сделаем рисунок.

Рассчитаем средний коэффициент эластичности по формуле:

= -0,04%.

Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,04%.

Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:

= 2,5%.

Построение степенной модели парной регрессии.

Уравнение степенной модели имеет вид: .

Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:

.

Произведем линеаризацию модели путем замены и . В результате получим линейное уравнение .

Рассчитаем его параметры, используя данные таблицы.

С учетом введенных обозначений уравнение примет вид: Y = A + BX – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы.

= -0,042.

= 5,418 – 0,959×5,26 = 5,637.

Перейдем к исходным переменным X и Y, выполнив потенцирование данного уравнения.

A = eA = e5,637 = 280,76

Получим уравнение степенной модели регрессии: .

Определим индекс корреляции

Используя данные таблицы, получим:

.

Рассчитаем коэффициент детерминации: = 0,1472= 0,021 = 2,1%.

Вариация результата Y всего на 2,1% объясняется вариацией фактора X.

Сделаем рисунок.

Для степенной модели средний коэффициент эластичности равен коэффициенту B.

= -0,042%.

Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,042%.

Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:

= 2,5%.

Сводная таблица вычислений

Для выявления формы связи между указанными признаками были построены полулогарифмическая и степенная модели регрессии. Анализ показателей корреляции, а также оценка качества моделей с использованием средней ошибки аппроксимации позволил предположить, что из перечисленных моделей более адекватной является степенная модель, поскольку для нее индекс корреляции принимает наибольшее значение R = 0,147, свидетельствующий о том, что между рассматриваемыми признаками наблюдается Слабая корреляционная связь.

Рассчитаем прогнозное значение результата по степенной модели регрессии, если прогнозируется увеличение значения фактора на 10% от среднего уровня.

Прогнозное значение составит:

= 193,5 × 1,1 = 212,9 тыс. р., тогда прогнозное значение Y составит:

= 224,6 тыс. р.

Определим доверительный интервал прогноза для уровня значимости a = 0,05.

Вычислим Среднюю стандартную ошибку прогноза По следующей формуле:

, где

Получаем: = 7,55.

Найдем предельную ошибку прогноза , где для доверительной вероятности 0,95 значение T составляет 1,96.

= 14,8.

Запишем доверительный интервал прогноза.

= 224,6 – 14,8 = 209,8 тыс. р.

= 224,6 + 14,8 = 239,4 тыс. р.

Таким образом, с вероятностью 0,95 можно утверждать, что прогнозное значение среднего размера назначенных ежемесячных пенсий будет находиться в пределах от 209,8 тыс. р. до 239,4 тыс. р.

Задание 3. Моделирование временных рядов

Имеются поквартальные данные по розничному товарообороту России в 1995-1999 гг.

Задания:

1. Построить график данного временного ряда. Охарактеризовать структуру этого ряда.

2. Рассчитать сезонную компоненты временного ряда и построить его Мультипликативную Модель.

3. Рассчитать трендовую компоненту временного ряда и построить его график

4. Оценить качество модели через показатели средней абсолютной ошибки и среднего относительного отклонения.

Решение: Пронумеруем указанные месяцы от 1 до 24 и построим график временного ряда.

Полученный график показывает, что а данном временном ряду присутствуют сезонные колебания.

Построим мультипликативную модель временного ряда.

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (S) и случайной (E) компонент.

Построение мультипликативной моделей сведем к расчету значений T, S и E для каждого уровня ряда.

Процесс построения модели включает в себя следующие шаги.

1)  Выравнивание исходного ряда методом скользящей средней.

2)  Расчет значений сезонной компоненты S.

3)  Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных T×E.

4)  Аналитическое выравнивание уровней T×E и расчет значений T с использованием полученного уравнения тренда.

5)  Расчет полученных по модели значений T×E.

6)  Расчет абсолютных и/или относительных ошибок.

Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:

1.1. Просуммируем уровни ряда последовательно за каждые четыре месяца со сдвигом на один момент времени и определим условные годовые уровни объема продаж (гр. 3 табл. 2.1).

1.2. Разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 2.1). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.

1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 5 табл. 2.1).

Таблица 2.1

Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 2.1). Эти оценки используются для расчета сезонной компоненты S (табл. 2.2). Для этого найдем средние за каждый месяц оценки сезонной компоненты Si. Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем месяцам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4.

Таблица 2.2

Имеем: 0,860 + 0,788 + 0,890 + 0,959 = 3,497.

Определяем корректирующий коэффициент: K = 4 : 3,497 = 1,144.

Скорректированные значения сезонной компоненты получаются при умножении ее средней оценки на корректирующий коэффициент K.

Проверяем условие: равенство 4 суммы значений сезонной компоненты:

0,984 + 0,901 + 1,018 + 1,097 = 4.

Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины (гр. 4 табл. 2.3), которые содержат только тенденцию и случайную компоненту.

Таблица 2.3

Шаг 4. Определим компоненту T в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни T×E. Составим вспомогательную таблицу.

Таблица 2.4

Вычислим параметры уравнения тренда.

= 0,17.

= 99,85.

В результате получим уравнение тренда:

T = 99,85 + 0,17×T.

Подставляя в это уравнение значения T = 1,2,…,16, найдем уровни T для каждого момента времени (гр. 5 табл. 2.3).

Шаг 5. Найдем уровни ряда, умножив значения T на соответствующие значения сезонной компоненты (гр. 6 табл. 2.3). На одном графике откладываем фактические значения уровней временного ряда и теоретические, полученные по мультипликативной модели.

Расчет ошибки в мультипликативной модели произведем по формуле:

Средняя абсолютная ошибка составила 1,0011 (см. гр. 7 табл. 2.3).

Рассчитаем сумму квадратов абсолютных ошибок .

Используя 5-й столбец таблицы 2.4, получим:

= 7,099.

Рассчитаем среднюю относительную ошибку: .

Используя 6-й столбец таблицы 2.4, получим, что средняя относительная ошибка составила 6,12%, т. е. построенная модель достаточно точно описывает динамику данного явления.

Формализованными
называют
методы прогнозирования, которые
используют математическое описание
выявленных закономерностей в развитии
объекта для получения прогноза.
Фактографические
ме­тоды прогнозирования используют
в качестве источника информации
действительно свершившиеся факты,
которые зафиксированы на ка­ком-либо
носителе информации с помощью
количественных или каче­ственных
характеристик.

Статистические
методы прогнозиро­вания,
основанные на выявленных в прошлом
закономерностях разви­тия объекта и
предположениях об инерционном развитии
объекта в бу­дущем на основе выявленных
математических закономерностей изменения
характеристик данного объекта с целью
получения прогнозных моделей.

Методы обработки
совокупностей включают осреднение
параметров одногодичных уравнений
регрессии, ковариационный анализ и др.

Имитационное
моделирование,
применяемое для анализа и прогнозирования
развития сложных систем, в которых
конечный результат зависит от множества
параметров. Дают возможность, анализируя
промежуточные результаты, менять в
процессе моделирования управляющие
параметры.

Историко-логический
анализ основан
на исследовании истори­ческих аналогий
в развитии разных объектов или одного
объекта в раз­ные периоды времени.

Методы
аналогий основаны
на выявлении сходства, общих черт в
закономерностях развития различных
процессов. К ним относятся методы
математических и исторических аналогий.

Опережающие
методы прогнозирования основаны
на опреде­ленных принципах специальной
обработки инфор­мации, учитывающих
ее свойство опережать практическое
применение инноваций. К ним относятся
методы исследования динамики
научно-технической информации,
использующие построение динамических
рядов на базе различных видов такой
информации, анализа и прогно­зирования
на этой основе развития соответствующего
объекта (например, метод огибающих,
патентный метод).

Результат
прогноза, разработанного формализованным
методом, чаще всего выражается
количественным показателем, которому
может быть дана точечная ()
и (или) интервальная оценка ().

Точечная
оценка ()
– это единичная оценка прогнозного
параметра. Прогноз должен быть дан в
виде интервала значений.

Интервальная
оценка ()
– это числовой интервал (довери­тельный
интервал), в котором, вероятно, находится
прогнозный па­раметр.

Точность
прогноза
тем выше, чем меньше величина ошибки,
ко­торая представляет собой разность
между прогнозируемыми и факти­ческими
значениями исследуемой величины.

Математическая
вероятность (Р_i)
случайной величины равна отношению
числа событий, благоприятствующих ее
появлению (т.е. свершению прогноза) к
общему числу событий (благоприятных и
неблагоприятных). Численное значение
вероятности прогноза лежит в пределах
от 0 до 1.

Границы доверительного
интервала можно задать такими широкими,
что прогнозируемое значение попадет
туда с любой вероятностью, включая Р =
0 и Р = 1. Такой прогноз называется абсолютно
достоверным. Однако границы доверительного
интервала будут столь широкими, что
полученный прогноз не будет иметь
практиче­ской ценности для принятия
управленческих решений. На практике
достаточно иметь вероятность прогноза
0,7-0,95.

Под
достоверностью
прогноза
понимается вероятность осуще­ствления
прогноза в заданном доверительном
интервале
.

Неформально
доверительный интер­вал может быть
определен экспертами с учетом степени
изменчивости фактических значений
показателей вокруг расчетных
(теоретических) значений в прошлом и
возможности деформации в будущем.
Суммарная ошибка решения прогнозной
задачи определяется по формуле

, (3.1)

где – суммарная ошибка;

–ошибки
информации, обусловленные неадекватностью
описания объек­та, погрешностями
получения и обработки информации;

–ошибки
метода прогнозирования, вызванные
невозможностью идеально­го выбора
метода для данного объекта, а также
обязательной схематично­стью метода;

–ошибки
вычислительных процедур;

–ошибки,
допущенные человеком и обусловленные
субъективными факто­рами (низкая
квалификация, восторженность, пессимизм);

–нерегулярная
составляющая ошибки, обусловленная
возможностью появления непредсказуемых
изменений в объекте.

Формально границы
доверительного интервала можно определить
на основе оценки изменчивости уровней
ряда. Чем выше эта изменчивость, тем
менее точной может быть расчетная
величина и тем шире должен быть
доверительный интервал при одной и той
же вероятности прогноза.

Получая
прогнозный результат в виде точечного
значения
,
необходимо указать и возможную величину
ошибки,
т.е. перейти к интервальному прогнозу
по формуле:

, (3.2)

где – точечное значение прогнозной
характеристики;

–интервальное
значение прогнозной характеристики;

–вероятная
ошибка прогноза.

Для определения
границ доверительного интервала
используется выражение

, (3.3).

где – среднеквадратическое отклонение;

–критерий
Стьюдента.

Величина
среднеквадратического отклонения
рассчитывается по формуле

, (3.4):

где – фактическое значение исследуемой
характеристики на участке ретроспекции;

–расчетное
значение исследуемой характеристики
на участке ретроспек­ции;

n
– число наблюдений (размер выборки).

Величина
определяет минимальную ошибку прогноза.

–критерий
Стьюдента, значение которого зависит
от размера выборочной совокупности и
заданной вероятности прогноза,
использование этого коэффициента
определяется ограниченностью выборки.
Критерий Стьюдента — чем выше заданная
вероятность прогноза и чем меньше размер
выборки, тем шире должны быть границы
доверительного интервала.

После наступления
прогнозируемого события ошибка прогноза
определяется как разность между
фактическим и прогнозным значе­нием
показателя. Ошибка прогноза или
погрешность для каждого момента времени,
в котором рассматривается прогноз:

, (3.5)

где –
ошибка прогноза в момент времениt;

–фактическое
значение в момент времени t;

–прогнозное
значение в момент времени t.

Способы оценки
средней ошибки прогноза (по­грешности):

■ среднее
абсолютное отклонение (mean
absolute
derivation,
MAD).
Использование этого показателя имеет
смысл, когда исследователю не­обходимо
оценить ошибку в тех же единицах, что и
исходный ряд:

; (3.6)

■ средняя
процентная ошибка (mean
percentage
error,
MPE)
по­зволяет оценить возможное смещение
прогноза, когда полученный про­гноз
окажется завышенным или заниженным).
При несмещенном про­гнозе имеем
величину ошибки, близкую к нулю, при
завышенном – большое положительное
процентное значение, при заниженном –
боль­шое отрицательное:

; (3.7)

■ средняя
абсолютная ошибка в процентах (mean
absolute
percentage
error,
МАРЕ):

. (3.8)

Модели динамики
данных:

Горизонтальную
модель используют,
если наблюдения колеб­лются относительно
постоянного уровня или среднего значения,
в этом случае временной ряд называют
стационарным. Внешние воздействия
относительно постоянны. Прогнозирование
включает использование его предыстории
для оценки среднего значения, которое
становится прогнозным. Используют
методы наивного прогнозирования,
простого среднего, скользящего среднего,
простое экспоненциальное сглаживание.

Трендовая
модель применяется,
если значения временного ряда возрастают
или убывают в течение некоторого,
достаточно большого промежутка времени.
Методы прогнозирования должны дать
возмож­ность выявить закономерность
и рассчитать параметры средней
тео­ретической линии развития объекта.
Оперируют методами прогнозной
экстраполяции, методы скользящей средней
и линейного экспонен­циального
сглаживания.

Сезонная
модель используется,
если на данные наблюдений влияют сезонные
факторы. В прогнозировании могут быть
использованы модели экстрапо­ляции
с аддитивной и мультипликативной
компонентой.

Циклическая
модель применяется,
если данные характеризуются подъемами
и спадами, не зависящими от времени.
Циклическая компонента обычно имеет
причиной общие закономерности
экономическо­го развития (жизненный
цикл продукции, деловой цикл, бизнес-цикл).
Методы прогнозирования – классическое
разложение, экономические индикаторы,
эконометрические модели, многомерная
регрессия.

Временной
(или динамический) ряд – это упорядоченная
вся времени совокупность измерений
одной из характеристик исследуемого
объекта (),t
– порядковый номер анализируемого
периода.

Интервальный
временной ряд –
это совокупность показателей, каждый
из которых характеризует развитие
объекта исследования за определенный
период времени (год, квартал, месяц,
сутки и т.п.).

Моментный
временной ряд –
это совокупность показателей
характеризующих состояние объекта на
определенную дату.

Наивное
прогнозирование основано
на предположении, что пре­дыдущее
значение лучше всего предсказывает
будущее.

Первый
вариант.
Прогнозное значение принимается равным
пре­дыдущему фактическому значению,
такой прогноз называют прогно­зом
без изменений:

, (3.9)

где – прогнозное значение в момент времениt;

–фактическое
значение в момент времени t
— 1.

Второй
вариант.
Наивный прогноз, который можно получить
учитывая последние абсолютные или
относительные изменения пока­зателей.
Он применяется, если значения фактических
величин изменяются во времени.

Методы
простых средних.
Прогнозное значение рассчитывается на
основе обобщенных средних характеристик
временного ряда в ретроспективном
периоде. К средним характеристикам
динамики относятся: средний уровень
ряда, или средняя хронологическая;
средний абсолютный прирост; средний
темп роста; средний темп прироста.

Показатель
рассчитывается различ­но для
интервальных и моментных рядов.

Для
интервального
ряда сумма
значений фактических показате­лей
временного ряда делится на число
показателей:

. (3.10)

Для
моментного
ряда расчет
осуществляется по формуле (3.11). Следует
учесть, что значения первого и последнего
показателей вре­менного ряда берутся
в половинном размере, поэтому в знаменателе
количество показателей уменьшается на
единицу.

. (3.11)

Средний
абсолютный прирост ряда показывает
скорость разви­тия явления и
рассчитывается по формуле

, (3.12)

где – первый зарегистрированный показатель
временного ряда;

y
– последний зарегистрированный
показатель временного ряда;

n
– число показателей временного ряда.

Средний
темп роста может
быть рассчитан по формуле средней
геометрической, при сравнении последнего
показателя временного ряда с первым
расчет осуществляется по формуле

. (3.13)

Средний
темп прироста определяется
по формуле

. (3.14)

Метод
простого скользящего среднего.
Прогноз строится с учетом не всех
наблюдений, а определенного количества
последних наблюдений. Как только новое
наблюдение становится доступным, оно
включается в расчетную формулу (3.15), а
наиболее старое исключается. Скользящее
среднее порядка
k
– это среднее значение k
последовательных наблюдений:

, (3.15)

где t
– количество измерений;

–значение
исследуемой характеристики в текущем
периоде;

–прогнозное
значение исследуемой характеристики
на следующий период;

k
– количество наблюдений в скользящем
среднем.

Величина
k
может принимать произвольно выбранное
значения (3, 4, 5 и т.д.). Величина k
зависит от размера изучаемой совокупности,
чем большее количество наблюдений
анализируется, тем большее значение
она может принимать.

Метод
двойного скользящего среднего. Временной
ряд сглаживается методом простого
скользящего среднего, а потом повторяется
процедура усреднения для рассчитанных
значений.

, (3.16)

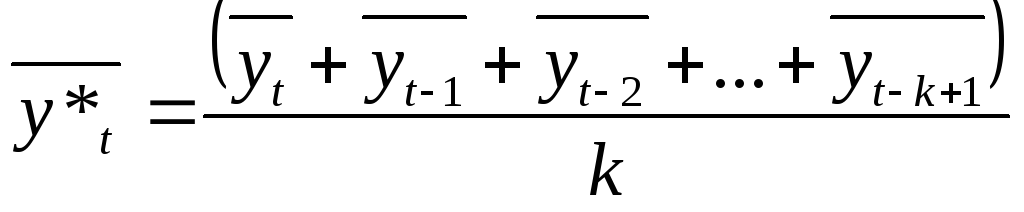
где – вторичное скользящее среднее.

Для
построения прогноза рассчитываются
сумма первичного скользящего среднего
и разницы между первичным и вторичным
скользящим средним
(3.17) и коэффициент корректировки:

; (3.17)

. (3.18)

Прогнозное значение
пар периодов вперед определяется по
формуле

. (3.19)

Экстраполяция
– метод
прогнозирования, основанный на ана­лизе
динамики объекта прогнозирования в
ретроспективном периоде. Метод
экстраполяции позволяет описать функцию,
характеризующую движение исследуемой
характеристики.

В процессе
экстраполяции определяют временной
ряд, тренд и случайную компоненту.
Формула временного ряда:

. (3.20)

Тренд
(эволюаторная составляющая, вековая
тенденция) – средняя линия движения
прогнозируемой характеристики ().

Случайная
компонента характеризует случайные
отклонения фактических показателей
динамики объекта от средней линии ().

Объективным
критерием оценки целесообразности
сглажи­вания может быть величина
абсолютного отклонения сглаженных
зна­чений от фактических:

, (3.21)

где – положительное число, выбираемое из
соображений точности представления
данных и точности последующих алгоритмов
обработки.

Выбор функции,
применяемой для описания явления,
зависит от типа динамики процесса. В
приложении 3 приведены основные
элементарные функции прогнозной
экстраполяции.

В социально-экономическом
прогнозировании экстраполяция применяется
для следующих типов динамики.

1. Равномерное
развитие, под которым понимают
экономический рост с постоянным
абсолютным приростом. Эта динамика
может быть описана ли­нейной функцией

, (3.22)

где а
– теоретическое значение y_t
в точке отсчета, t
– 0;

b
– коэффициент регрессии, определяющий
направление развития исследуе­мой
характеристики (если b
> 0, показатели
временного ряда равномерно возрастают,
если b
< 0, показатели
временного ряда равномерно убывают,
если b
= 0, показатели
временного ряда неизменны во времени).

2. Равноускоренное
(равнозамедленное) развитие — экономический
рост с постоянными темпами прироста.
Дан­ный тип динамики может быть описан
функцией параболы второго порядка,
показательной или экспоненциальной
функциями. Уравне­ние параболической
функции имеет следующий вид:

, (3.23)

где с
– постоянное изменение интенсивности
развития (в единицу времени).

Если
с >
0, то для процесса характерно ускорение
динамики, если с
< 0 –
замедление. При этом параметр b
может принимать положительные или
отрицательные значения.

3. Развитие с
переменным ускорением (замедлением) —
экономический рост со стабильно
изменяющимися темпами прироста. Динамика
может быть описана кубической параболой:

, (3.24)

Для нахождения
параметров функции решаются определенные
системы уравнений, которые приведены
в приложении 4.

Экстраполяция на
основе полученных функций дает возможность
получить точечное прогнозное значение.
Следующий этап – переход от точечного
прогноза к интервальному:

, (3.25)

где –
интервальное значение прогнозной
характеристики в момент времениt;

–точечное
значение прогнозной характеристики в
момент времени t;

–ошибка
прогноза.

Расширение границ
доверительного интервала при линейном
тренде, вследствие дисконтирования
прогнозной информации, учиты­вается
коэффициентом:

, (3.26)

где l
– безразмерный интервал периода
упреждения прогноза;

n
– число наблюдений на участке
ретроспекции.

Длина интервала
периода упреждения прогноза численно
равна временному шагу между ретроспективными
значениями.

Формула расчета
гра­ниц доверительного интервала
примет следующий вид:

.
(3.27)

Для выяснения
закономер­ностей необходимо полу­чить
надежно повторяемые и достаточно
достоверные многократные сов­падения
ожидаемых величин и фактических значений.
Исследование динамики экономических
показателей может привести к открытию
новых зависимостей, которые не всегда
очевидны и доступны для других методов.

Под
сезонностью
понимается устойчивая, повторяющаяся
во времени периодичность в развитии
экономических явлений. Исследовать
влияние сезонности можно по временным
рядам, содержащим информацию о значениях
показателя по кварталам, месяцам, недели,
дням, времени суток или часам.

В процессе
прогнозирования сезонных изменений
каждый уро­вень временного ряда можно
представить как результат взаимодействия
трендовой, сезонной и случайной компонент.

Модель
с аддитивной компонентой
строится путем сложения составляющих.
Уравнение временного ряда с учетом
сезонных колеба­ний может быть
представлено формулой:

, (3.28)

где – сезонная компонента;

L
– номер сезона.

Модель с аддитивной
компонентой целесообразно использовать,
если среднегодовые значения показателя
остаются неизменными на протяжении
длительного периода.

Модель
с мультипликативной компонентой
строится путем перемножения трендовой
составляющей и индекса сезонности ()
, соответственно, уравнение временного
ряда может быть представлено фор­мулой

.
(3.29)

Этапы
построения прогнозной модели
с аддитивной компонентой:
построение и визуальный анализ графика
сезонной волны; расчет значений сезонной
компоненты; десезонализация данных,
т.е. вычитание сезонной компоненты из
фактических значений; расчет тренда на
основе полученных десезонализированньи
данных; оценка ошибки для оценки степени
соответствия модели исходным данным,
расчет среднеквадратического отклонения;
построение прогноза с учетом сезонных
колебаний.

Последовательность
этапов построение модели с
мультипликативной компонентой
(первый способ): расчет значений индекса
сезонности; десезонализация данных,
т.е. деление фактических значений на
индекс сезонности; расчет параметров
тренда для полученных десезонализированных
данных; оценка ошибки для оценки степени
соответствия модели ис­ходным данным;
расчет среднеквадратического отклонения;
построение прогноза с учетом сезонных
колебаний.

Последовательность
этапов построение модели с
мультипликативной компонентой (второй
способ): определение вида тренда и расчет
параметров тренда без уче­та сезонных
колебаний; построение и визуальный
анализ графика сезонной волны; расчет
индексов сезонности.

Формула индекса
сезонности, определенного по средней
арифметической, будет иметь следующий
вид:

, (3.30)

где –
фактическое значение исследуемой
характеристики в момент времениj;

–теоретическое
значение исследуемой характеристики
в момент времени j;

j
– номер измерения 1-х
сезонов в рассматриваемом временном
интервале;

l
– номер сезона;

k
– количество l-х
сезонов в рассматриваемом временном
интервале.

Расчет
скорректированных индексов сезонности.
Индекс корректировки можно определить
по формуле (3.31), а скорректированные
индексы сезонности рассчитать по формуле
(3.32). Далее при прогнозировании используются
именно скорректированные индексы
сезонности:

;
(3.31)

. (3.32)

Формирование
уравнений тренда с учетом индексов
сезонно­сти (3.33). Эта формула должна
быть конкретизирована для каждого типа
динамики, т.е. для равномерного развития
будет рассчитываться по формуле линейной
зависимости, для равноускоренного –
по степен­ной или параболической:

.
(3.33)

Рассчитанные
по уравнению (3.33) прогнозные характеристики
отражают и закономерности среднегодовой
динамики исследуемой ха­рактеристики
и среднесезонные отклонения от нее.

С количественной
точки зрения различают три вида
взаимосвязей: балансовые; компонентные;
факторные.

Балансовая
связь
показателей характеризует соответствие
двух элементов — спроса и предложения,
доходов и расходов, производства и
потребления, наличия рабочей силы и
потребностей в ней и т.п. Методический
инструмент прогнозирования балансовых
связей – балансы и разрабатываемые на
их основе балансовые модели.

Компонентные
связи
показателей характеризуются из­менением
прогнозного показателя – результат
изменения компонентов, входящих в этот
показатель как множители. В прогно­зировании
этот вид взаимосвязи может быть
использован для опреде­ления прогноза
одного из показателей при известных
прогнозах компонентов, используемых
при расчете искомой характеристики
(ме­тод укрупненных измерителей, метод
Кольма) либо для оценки качества прогнозов
взаимосвязанных показателей.

Факторные
связи
характеризуются тем, что проявляются
в согласованной вариации изучаемых
показателей. При этом одни показа­тели
выступают как факторные (причины,
независимые переменные), другие – как
следствие (результат, зависимая
переменная). По своему характеру этот
вид связи – причинно-следственная
зависимость.

Факторные
связи могут рассматриваться как
функциональные или корреляционные. При
функциональной связи
изменение результативного признака
всецело обусловлено действием факторного.
При
корреляционной связи
изменение результативного признака
лишь частично обусловлено влиянием
факторного признака, так как не исключается
возможность воздействия и других
факторов.

Корреляционно-регрессионный
анализ используется
для исследования форм связи, устанавливающих
количественные соотношения между
случайными величинами изучаемого
процесса. При этом значение независимой
переменной (х)
нам известно по предположению. В процессе
прогнозирования оно может быть
использовано нами для оценки зависимой
переменной (y).
Функция регрессии
показывает, каким будет в среднем
значение переменнойy,
если переменные х
примут конкретное значение.

Переменная
у,
характеризующая результат, формируется
пот воздействием других переменных и
факторов. Поэтому она всегда стохастична
(случайна) по природе. Переменные х
(объясняющие переменные) характеризуют
причину. Значения ряда переменных x
могут характеризовать внутренние
элементы системы или задаваться «извне»
прогнозируемой системы.

По
своей природе объясняющие переменные
могут быть случайными и неслучайными.
Регрессионные остатки
– это латентные (скрытые) случайные
компоненты, влияющие нау,
а также случайные ошибки в измерении
анализируемых результирующих переменных.

Парная
корреляция –
корреляционные связи между двумя
переменными. Экономико-математические
модели, построенные с учетом такого
рода взаимосвязей, называют однофакторными
моде­лями.

Множественная
корреляция –
корреляционные взаимосвязи между
несколькими переменными.

Ложная
корреля­ция –
это отсутствие причинной связи между
явлениями, связанными корреляционной
связью.

Регрессионный
анализ –
решаются задачи выбора независимых
переменных, существенно влияющих на
зависимую величину, определенней формы
уравнения регрессии, оценивание
параметров.

Последовательность
процедур прогнозирования на основе
однофакторных моделей линейной регрессии:

1. Сбор исходной
информации.

2. Качественный
анализ взаимосвязи исследуемых
показателей, определение причинно-следственной
связи между анализируемыми характеристиками.

3.
Оценка тесноты связи. Коэффициент
корреляции R
характеризует тесноту связи между
случайными величинами (х,у),
может быть рассчитан по формуле

. (3.34)

По численному
значению коэффициента корреляции можно
сделать следующие выводы:

R
= 0 –
рассматриваемые величины не взаимосвязаны;

R
= 1 – имеет
место прямая функциональная зависимость,
изменение значений переменных
однонаправленное, при увеличении одной
переменной другая тоже увеличивается;

R
= — 1 – имеет
место обратная функциональная зависимость,
изменение значений переменных
разнонаправленное, при увеличении одной
переменной другая уменьшается.

По абсолютному
значения коэффициента корреляции можно
прийти к следующим заключениям:

–связи
практически нет;

–связь
слабая;

–связь
заметная;

–связь
тесная;

–связь,
близкая к функциональной.

Прогнозы строятся
на основе взаимосвязей с коэффициентом
корреляции 0,75-1.

4.
Расчет параметров уравнения регрессии.
Оценка параметров уравнения регрессии
осуществляется методом наименьших
квадратов на основе формул (3.35), (3.36),
(3.37):

; (3.35)

; (3.36)

, (3.37)

где n
– объем выборки.

5. Оценка значимости,
типичности.

6.
Задание условий прогнозного периода
(вероятных значений параметра х).

7.
Прогнозирование возможных значений
параметра y
при задан­ных значениях параметра х.

Временным
лагом ()
называется промежуток времени, по
истечении которого изменение показателей
одного временного ряда оказывает влияние
на показатели другого. Корреляционно-регрессионная
зависимость с учетом временного лага
описана следующим уравнением:

. (3.38)

Авторегрессионной
называют
модель, в которой лаговое соотношение
связывает значение одного и того же
показателя в разные моменты времени:

. (3.39)

Экономический
барометр –
это система экономических показателей,
применяемых для анализа и прогнозирования
конъюнктуры рынка. Все показатели
делятся на три группы: опережающие
(лидирующие), со­впадающие (синхронные)
и запаздывающие.

Во
многих прогнозах ставится вопрос не о
запаздывании, а об упреждении событий.
По предположению принимается прогнозное
значение
,
и рассчитывается необходимая величина
.

Интуитивные
(экспертные) методы прогнозирования –
это методы прогнозирования, использующие
в качестве источника инфор­мации
обработанные суждения экспертов,
полученные в ходе проведе­ния
специальных опросов.

Индивидуальные
экспертные оценки –
методы прогнозирования, основанные на
использовании в качестве источника
информации одного эксперта.

Прямой
опрос (интервью).
Прогноз составляется по результатам
беседы прогнозиста (интервьюера) с
экспертом, в ходе которой прогнозист
задает вопросы в соответствии с заранее
разработанной программой.

Анонимный
опрос предполагает
самостоятельную творческую работу
эксперта по поставленной проблеме.

Аналитические
докладные записки.
Прогнозная информация представленная
в форме докладной записки, является
результатом длительной, тщательной
самостоятельной работы эксперта над
анализом прогнозируемого объекта.

Коллективные
экспертные оценки –
методы прогнозирования, основанные на
выявлении обобщенной объективизированной
оценки экспертной группы в результате
обработки индивидуальных независимых
оценок, вынесенных экспертами, входящими
в группу. Зависимый интеллектуальный
эксперимент проводится путем коллективного
обсуждения исследуемой проблемы.
Независимый интеллектуальный эксперимент
проводится с помощью анкетирования.

Оценка компетентности
экспертов. Составляется рабочая таблица
– «Матрица оценки компетентности
экспертов первого порядка», по результатам
которой рассчитываются коэффициенты
компетентности экспертов первого
порядка:

. (3.40)

По результатам
этих расчетов строится матрица оценки
коэффи­циентов компетентности
экспертов второго порядка, оцен­ки в
которой взвешиваются с учетом
компетентности эксперта, давше­го
оценку, и рассчитывается коэффициент
компетентности экспертов второго
порядка:

, (3.41)

где – результат анкетирования, заключение
данноеi-м
экспертом по поводу компетентности
j-го
эксперта;

I
– номер оценивающего эксперта;

j
– номер оцениваемого эксперта;

,
если i-й
эксперт назвал j-ro
эксперта;

,
если i-й
эксперт не назвал j-го
эксперта;

–коэффициент
компетентности первого порядка j-гo
эксперта, показывает долю голосов,
полученных j-м
экспертом, в общей сумме голосов.

Оценка профессиональных
качеств эксперта способом самооценки
предполагает наличие тестов, анкет, на
вопросы которых эксперту предстоит
дать самостоятельный ответ. Каждый
ответ на вопрос получает определенное
количество баллов, соответствующее, с
одной стороны, значимости оцениваемого
показателя, а с другой – варианту ответа
эксперта на данный вопрос. Конкретные
численные значения весовых коэффициентов
определяются рабочей группой и не
сообщаются потенциальным экспертам.
Коэффициент компетентности конкретного
эксперта может быть получен как частное
от деления количества баллов данного
эксперта на количество баллов, которое
может получить «эталонный» эксперт:

, (3.42)

где – количество баллов, полученноеj-м
экспертом при ответе на i-й
вопрос анкеты;

–количество
баллов, которое может получить «эталонный»
эксперт при ответе на i-й
вопрос анкеты.

Зависимый
интеллектуальный эксперимент проводится
путем коллективного обсуждения
исследуемой проблемы, в результате
которого эксперты вырабатывают обобщенную
прогнозную оценку. К методам данной
группы могут быть отнесены методы
комиссий (совещание), суда и мозговой
атаки.

Метод
деструктивной отнесенной оценки (ДОО).

Основные этапы
ДОО: формирование группы участников
мозговой атаки: составление проблемной
записки участника моз­говой атаки —
описание сущности и основных процедур
метода ДОО и описание проблемной
ситуации; генерация идей; систематизация
идей; разрушение систематизированных
идей; оценка критических замечаний и
составление списка практически
осуществимых идей.

Метод
обмена мнениями.
Группе экспертов предлагают крити­чески
обсудить заранее подготовленный прогноз.
В процессе мозговой атаки необходимо
найти уязвимые места в первоначальном
прогнозе и превратить его в согласованный
документ.

Операционное
творчество.
Только руководитель группы знает
истинный характер проблемы и организует
обсуждение таким образом, чтобы найти
решение.

Независимый
интеллектуальный эксперимент
проводится заочно с помощью анкетирования.
К числу его методов могут быть отнесены
социологические опросы, анкетирование
методом Дельфи, метод ранговой корреляции
и др.

Обработка
и представление результатов коллективных
экспертных опросов.
Способ обработки результатов экспертизы
зависит oт
природы исследуемых факторов и типа
шкалы результатов, требуемых точности
и оперативности получения необходимых
характеристик.

При прогнозировании
методами коллективных экспертных оценок
важно установить среднюю оценку
экспертной группы. Используют следующие
показатели: среднее значение прогнозируемой
величины, дисперсию, коэффициент
вариа­ции оценок.

Среднее
значение прогнозируемой величины ()
определяется по формуле

, (3.43)

где – значение прогнозируемой величины,
данноеi-м
экспертом;

n
– число экспертов в группе.

При известных
коэффициентах компетентности экспертов
кор­ректнее применять среднюю
взвешенную оценку, используя в качестве
весов коэффициенты компетентности:

. (3.44)

Дисперсия
значений прогнозируемой величины (D):

. (3.45)

Среднеквадратическое
отклонение индивидуальных экспертных
оценок ():

. (3.46)

Коэффициенты
вариации оценок, данных экспертами (v):

. (3.47)

Метод
Дельфи –
метод коллективного экспертного
поискового прогнозирования, основанный
на выявлении согласованной оценки
экспертной группы путем анонимного
опроса экспертов в несколько туров,
предусматривающий сообщение экспертам
результатов предыдущего тура с целью
дополнительного обоснования оценки
экспертов в последующем туре.

Обработка информации,
полученной методом Дельфи.

1. Получение ответов
на вопросы от экспертов в письменной
форме.

2. Статистическая
обработка – расчет медианы, моды,
кварти­лей и децилей. Для этого
необходимо первоначально упорядочить
по­лученные экспертные оценки по
возрастанию или убыванию прогно­зируемого
признака.

Медиана
— значение прогнозиру­емого признака,
которым обладает центральный член ряда,
составлен­ного в порядке возрастания
значений признака (ответ эксперта в
центре ранжированного ряда). Мода
— наиболее
часто встречающееся в ранжиро­ванном
ряду значение прогнозируемого признака.

Квартиль
– значение прогнозируемого признака,
которым обла­дают члены ряда под
номером, представляющим 1/4 всего ряда
(ниж­ний квартиль) и 3/4 всего ряда
(верхний квартиль).

Дециль
– это значение прогнозируемого признака,
которым об­ладают члены ряда под
номером, представляющим 1/10, всего ряда
и 9/10 всего ряда.

В результате
статистической обработки вся совокупность
отве­тов разбивается на несколько
групп и выделяется 80- и 50%-ный кори­дор
ответов.

3. Экспертам
присылается анкета, в которой сообщаются
резуль­таты анализа, обобщенные в
двух разделах. В первом дан перечень
пунк­тов, по которым большинство
экспертов дали согласованную оценку.
Во втором разделе отобраны недостаточно
согласованные оценки.

4. Повторное
анкетирование и обработка его результатов.

Согласованность
мнений эк­спертов может быть оценена
коэффициентом конкордации.

Коэффициент
конкордации (W)
показывает степень согласованности
мнений экспертов по важности каждого
из оцениваемых направ­лений:

, (3.48)

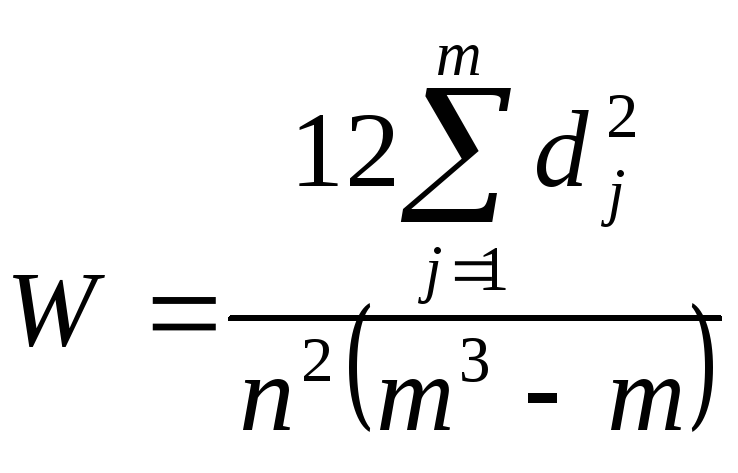
где n
– количество экспертов;

m
– количество параметров (направлений,
оцениваемых объектов);

–отклонение
суммы рангов по j-му
направлению от среднего значения рангов.

Если среди рангов,
данных одним экспертом, есть равные,
формула оценки согласованности экспертных
оценок приобретает следующий вид:

, (3.49)

если W
= 1 – полная
согласованность мнений экспертов;

W
= 0 – полная
несогласованность мнений экспертов.

Последовательность
расчетов методом ранговой корреляции.

1. Получение
индивидуальных экспертных оценок
относитель­но важности, значимости,
приоритетности оцениваемых параметров
или направлений. Оценки даются в виде
весовых коэффициентов (от 0 до 1). Сумма
коэффициентов одного эксперта, должна
равняться 1.

2.
Ранжирование оценок важности, данных
экспертами. Каждая оценка, данная i-м
экспертом, выражается рангом
(число натурального ряда) таким образом,
что значение 1 – максимальная оценка,a
n
– минимальная. Если среди оценок, данных
i-м
экспертом есть одинаковые, то им
присваивается одинаковый ранг, равный
среднему арифметическому соответствующих
чисел натурального ряда.

3.
Расчет суммы рангов по каждому направлению
():

. (3.50)

4.
Расчет среднего значения суммы рангов
по всем направлениям ():

, (3.51)

где m
– количество оцениваемых направлений;

j
– номер направления.

5.
Расчет отклонения суммы рангов по j-му
направлению от сред­него значения
суммы рангов ():

. (3.52)

6.
Расчет показателя
характеризующего равные ранги:

, (3.53)

где – количество равных рангов вi-й
группе.

7. Расчет коэффициента
конкордации, выводы о согласованнос­ти
мнений экспертов.

8. Анализ значимости
исследуемых параметров. Параметр с
наи­меньшей суммой рангов имеет
наибольшее значение. Средний коэф­фициент
весомости определяется как отношение
величины обратной сумме рангов к их
сумме:

. (3.54)

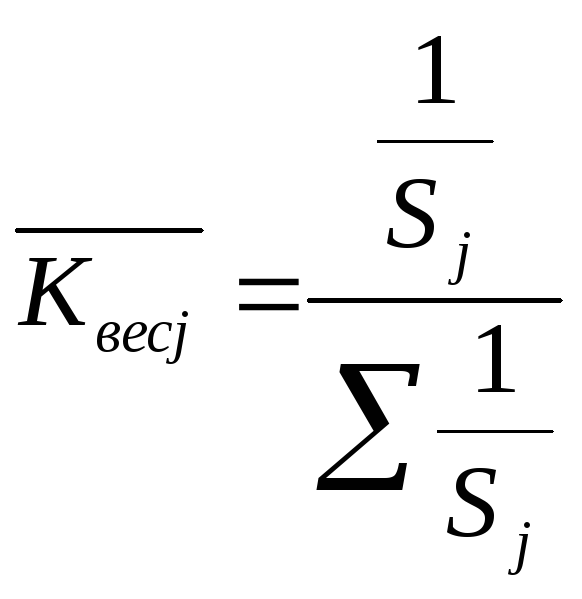
Степень предпочтения
параметров заранее считается неизвестной,
она определяется в результате обработки
полученных оценок. Результаты оцени­вания
фиксируются в виде квадратной матрицы
смежности парных сравнений в виде
знаков:

■ >,
если
;

■ <,
если
;

■ =,
если
.

Далее
строится квадратная матрица
,
где,
если,,
если,,
если,
гдеу
– любое рациональное число в заданном
интервале.

Далее
в расчет вводится понятие «итерированная
сила» порядка, «К»
параметров в виде матрицы-столбца Р(К),
которая определяется в общем случае
как:

, (3.55)

где К
=1,2, … m.

Итерированная
сила объекта х
– произведение строки матрицы А
на столбец матрицы Р(К)
по формуле:

. (3.56)

В
начале расчета принимается итерированная
сила Р(К) = 1,
т.е. для определения
берется.
Исходная матрицаА
умножается на
.
Далее этот процесс продолжается с учетом
полученной итериро­ванной силы
предыдущей итерации.

Практическую
ценность представляет нормированная
итерированная сила k-го
порядка i-го
пара­метра
,
она трактуется как значение коэффициента
ве­сомостиi-го
параметра:

; (3.57)

. (3.58)

С каждой последующей
итерацией результаты уточня­ются.

Морфологический
анализ –
метод предпрогнозных исследова­ний,
основанный на формировании и анализе
максимального числа вариантов развития
или состояния объекта прогнозирования
с после­довательным исключением
нереальных или наименее целесообразных,
варианты морфологических подходов к
прогнозированию: метод морфологических
деревьев, метод ступенчатого поиска
решения, функционально-стоимостной
анализ, метод принудительного образования
связей, метод отрицания и конструирования,
метод крайностей, метод сопоставления
совершенного с дефектным.

Последовательность
построения «морфологического ящика».

1. Точная формулировка
поставленной цели или проблемы.

2.
Структурирование объекта исследования.
Выделение и изучение парамет­ров (),
от которых зависит решение проблемы.

3.
Нахождение для каждого выделенного
параметра ()
его значенийи сведение их в «морфологический ящик».
Значения параметров независимы и
несводимы.

4.
Нахождение вариантов решения проблемы.
Возможный вариант решения – любая
совокупность значений всех параметров
(по одному значению из каждой строки
«морфологического ящика»). Общее число
вариантов решения проблемы (N)
определяется по формуле

, (3.59)

где – число значенийi-го
параметра ().

5. Определение
функциональной ценности всех полученных
в «мор­фологическом ящике» вариантов.
В результате оценки варианты решения
проблемы ранжируются по уровню избранного
критерия, из полученной их совокупности
исключаются неосуществимые и признанные
на прогнозный период нецелесообразными.

6. Выбор наиболее
желательного или наиболее реального
варианта решения.

Прогнозный
сценарий –
метод предпрогнозных исследова­ний,
с помощью которого устанавливается
логическая последователь­ность
событий для определения будущего
состояния объекта исследования. При
прогнозировании социально-экономических
проблем в сценарии указываются
альтернативные события и вероятные
сроки их наступления.

В результате
сценарного исследования эксперт
оформляет доклад, в который включаются
разделы: предисловие: описание сущности
и назначения сценариев; краткое описание
теоретических и информационно-статистических
оснований исследования, временного
горизонта; описание разработанных
вариантов; сравнение вариантов между
собой; рекомендации для процесса принятия
решений; выводы.

Литература: 1, 10, 15.

В статистика, а ошибка прогноза разница между фактическим или реальным и прогнозируемым или прогноз стоимость Временные ряды или любое другое интересное явление. Поскольку ошибка прогноза выводится из одного и того же масштаба данных, сравнение ошибок прогноза разных рядов может быть выполнено только в том случае, если ряды имеют одинаковый масштаб.^[1]

В простых случаях прогноз сравнивается с результатом в один момент времени, и сводка ошибок прогноза строится по набору таких моментов времени. Здесь прогноз может быть оценен с использованием разницы или пропорциональной ошибки. По соглашению ошибка определяется с использованием значения результата минус значение прогноза.

В других случаях прогноз может состоять из прогнозируемых значений за несколько периодов времени; в этом случае для оценки ошибки прогноза может потребоваться рассмотреть более общие способы оценки совпадения временных профилей прогноза и результата. Если основное применение прогноза состоит в том, чтобы предсказать, когда определенные пороговые значения будут пересечены, один из возможных способов оценки прогноза — использовать временную ошибку — разницу во времени между тем, когда результат пересекает порог, и тем, когда прогноз это делает. Когда есть интерес к достижению максимального значения, оценка прогнозов может быть выполнена с использованием любого из:

• разница времен пиков;
• разница пиковых значений в прогнозе и исходе;
• разница между пиковым значением результата и значением, прогнозируемым на этот момент времени.

Ошибка прогноза может быть ошибкой календарного прогноза или ошибкой перекрестного прогноза, когда мы хотим суммировать ошибку прогноза по группе единиц. Если мы наблюдаем среднюю ошибку прогноза для временного ряда прогнозов для одного и того же продукта или явления, мы называем это ошибкой календарного прогноза или ошибкой прогноза временного ряда. Если мы наблюдаем это для нескольких продуктов за один и тот же период, то это перекрестная ошибка производительности. Прогнозирование эталонного класса был разработан для уменьшения ошибки прогноза. Также было показано, что комбинирование прогнозов снижает ошибку прогноза.^[2][3]

Расчет ошибки прогноза

Ошибка прогноза — это разница между наблюдаемым значением и его прогнозом на основе всех предыдущих наблюдений. Если ошибка обозначена как тогда ошибку прогноза можно записать как;

где,

= наблюдение

= обозначают прогноз на основе всех предыдущих наблюдений

Ошибки прогноза можно оценить с помощью различных методов, а именно: средняя процентная ошибка, среднеквадратичная ошибка, средняя абсолютная ошибка в процентах, среднеквадратичная ошибка. Другие методы включают сигнал слежения и смещение прогноза.

Для ошибок прогноза по обучающим данным

обозначает наблюдение и это прогноз

Для ошибок прогноза на тестовых данных

обозначает фактическое значение наблюдения h-шага, а прогноз обозначается как

Академическая литература

Дреман и Берри в 1995 г. в «Financial Analysts Journal» утверждали, что прогнозы аналитиков ценных бумаг слишком оптимистичны и что инвестиционное сообщество слишком сильно полагается на их прогнозы. Однако этому противостоял Лоуренс Д. Браун в 1996 году, а затем снова в 1997 году, который утверждал, что аналитики, как правило, более точны, чем аналитики «наивных или сложных моделей временных рядов», и что ошибки не увеличиваются с течением времени.^[4][5]

Хиромичи Тамура в 2002 году утверждал, что консенсусные аналитики не только представляют свои оценки доходов, которые в конечном итоге близки к консенсусу, но и что их личные качества сильно влияют на эти оценки.^[6]

Примеры ошибок прогнозирования

Майкл Фиш — За несколько часов до Великая буря 1987 года сломался, 15 октября 1987 года, он сказал во время прогноза: «Ранее сегодня, по всей видимости, женщина позвонила на BBC и сказала, что слышала, что был ураган в дороге. Что ж, если вы смотрите, не волнуйтесь, его нет! ». буря было хуже всего ударить Юго-Восточная Англия за три столетия, в результате чего был нанесен рекордный ущерб и погибло 19 человек.^[7]

Великая рецессия — Финансово-экономический кризис разразился в 2007 году — возможно, худший со времен Великая депрессия 1930-х годов — не предвиделось большинством прогнозистов, даже если несколько одиноких аналитиков предсказывали это в течение некоторого времени (например, Нуриэль Рубини и Роберт Шиллер ). Неспособность спрогнозировать «Великая рецессия «вызвало много душевных поисков в профессии. Королева Великобритании Елизавета сама спросила, почему никто не заметил, что кредитный кризис приближается, и группа экономистов — экспертов из бизнеса, Сити, его регулирующих органов, академических кругов и правительство — пытался объяснить в письме.^[8]

Это было не только предсказание Великой рецессии, но и ее влияние, когда было ясно, что экономисты боролись. Например, в Сингапуре Citi утверждал, что страна испытает «самую серьезную рецессию в истории Сингапура». В 2009 году экономика выросла на 3,1%, а в 2010 году в стране наблюдался рост на 15,2%.^[9][10]

В конце 2019 года Международный Валютный Фонд по оценкам, глобальный рост в 2020 году достигнет 3,4%, но в результате коронавирус пандемия МВФ пересмотрел свою оценку в ноябре 2020 года, ожидая сокращения мировой экономики на 4,4%.^[11][12]

Смотрите также

• Расчет точности прогноза спроса
• Ошибки и неточности в статистике
• Прогнозирование
• Точность прогнозов
• Среднеквадратичная ошибка прогноза
• Смещение оптимизма
• Прогнозирование эталонного класса

использованная литература

Основной задачей при управлении запасами является определение объема пополнения, то есть, сколько необходимо заказать поставщику. При расчете этого объема используется несколько параметров — сколько будет продано в будущем, за какое время происходит пополнение, какие остатки у нас на складе и какое количество уже заказано у поставщика. То, насколько правильно мы определим эти параметры, будет влиять на то, будет ли достаточно товара на складе или его будет слишком много. Но наибольшее влияние на эффективность управления запасами влияет то, насколько точен будет прогноз. Многие считают, что это вообще основной вопрос в управлении запасами. Действительно, точность прогнозирования очень важный параметр. Поэтому важно понимать, как его оценивать. Это важно и для выявления причин дефицитов или неликвидов, и при выборе  программных продуктов для прогнозирования продаж и управления запасами.

В данной статье я представила несколько формул для расчета точности прогноза и ошибки прогнозирования. Кроме этого, вы сможете скачать файлы с примерами расчетов этого показателя.

Статистические методы

Для оценки прогноза продаж используются статистические оценки Оценка ошибки прогнозирования временного ряда. Самый простой показатель – отклонение факта от прогноза в количественном выражении.

В практике рассчитывают ошибку прогнозирования по каждой отдельной позиции, а также рассчитывают среднюю ошибку прогнозирования. Следующие распространенные показатели ошибки относятся именно  к показателям средних ошибок прогнозирования.

К ним относятся:

MAPE – средняя абсолютная ошибка в процентах

где Z(t) – фактическое значение временного ряда, а   – прогнозное.

Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE. 

Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.

MAE – средняя абсолютная ошибка

                                                                                                  .

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.

После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.

Кроме указанных методов иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.

ME – средняя ошибка

Встречается еще другое название этого показателя — Bias (англ. – смещение) демонстрирует величину отклонения, а также — в какую сторону прогноз продаж отклоняется от фактической потребности. Этот индикатор показывает, был ли прогноз оптимистичным или пессимистичным. То есть, отрицательное значение Bias говорит о том, что прогноз был завышен (реальная потребность оказалась ниже), и, наоборот, положительное значение о том, что прогноз был занижен. Цифровое значение показателя определяет величину отклонения (смещения).

MSE – среднеквадратичная ошибка

.

RMSE – квадратный корень из среднеквадратичной ошибки

.

.

SD – стандартное отклонение

где ME – есть средняя ошибка, определенная по формуле выше.

Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме ниже. Скачать пример расчета в Excel >>>

Связь точности и ошибки прогнозирования

В начале этого обсуждения разберемся с определениями.

Ошибка прогноза — апостериорная величина отклонения прогноза от действительного состояния объекта. Если говорить о прогнозе продаж, то это показатель отклонения фактических продаж от прогноза.

Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.

Точность прогноза в % = 100% – MAPE, встречается еще название этого показателя Forecast Accuracy. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности. Показатель точности прогноза выражается в процентах:

• Если точность прогноза равна 100%, то выбранная модель описывает фактические значения на 100%, т.е. очень точно. Нужно сразу оговориться, что такого показателя никогда не будет, основное свойство прогноза в том, что он всегда ошибочен.
• Если 0% или отрицательное число, то совсем не описывает, и данной модели доверять не стоит.

Выбрать подходящую модель прогноза можно с помощью расчета показателя точность прогноза. Модель прогноза, у которой показатель точность прогноза будет ближе к 100%, с большей вероятностью сделает более точный прогноз. Такую модель можно назвать оптимальной для выбранного временного ряда.  Говоря о высокой точности, мы говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Не имеет значения, что именно вы будете отслеживать, но важно, чтобы вы сравнивали модели прогнозирования или целевые показатели по одному показателю – ошибка прогноза или точность прогнозирования.

Ранее я использовала оценку MAPE, до тех пор пока не встретила формулу, которую рекомендует Валерий Разгуляев. 

Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>

Оценка ошибки прогноза – формула Валерия Разгуляева (сайт http://upravlenie-zapasami.ru/)

Одной из самых используемых формул оценки ошибки прогнозирования является следующая формула:

где: P – это прогноз, а S – факт за тот же месяц. Однако у этой формулы есть серьезное ограничение — как оценить ошибку, если факт равен нулю? Возможный ответ, что в таком случае D = 100% – который означает, что мы полностью ошиблись. Однако простой пример показывает, что такой ответ — не верен:

Оказывается, что в варианте развития событий №2, когда мы лучше угадали спрос, чем в варианте №1, ошибка по данной формуле оказалась – больше. То есть ошиблась уже сама формула. Есть и другая проблема, если мы посмотрим на варианты №2 и №3, то увидим, что имеем дело с зеркальной ситуацией в прогнозе и факте, а ошибка при этом отличается – в разы!.. То есть при такой оценке ошибки прогноза нам лучше его заведомо делать менее точным, занижая показатель – тогда ошибка будет меньше!.. Хотя понятно, что чем точнее будет прогноз – тем лучше будет и закупка. Поэтому для расчёта ошибки Валерий Разгуляев рекомендует использовать следующую формулу:

В таком случае для тех же примеров ошибка рассчитается иначе:

Как мы видим, в варианте №1 ошибка становится равной 100%, причём это уже – не наше предположение, а чистый расчёт, который можно доверить машине. Зеркальные же варианты №2 и №3 – имеют и одинаковую ошибку, причём эта ошибка меньше ошибки самого плохого варианта №1. Единственная ситуация, когда данная формула не сможет дать однозначный ответ – это равенство знаменателя нулю. Но максимум из прогноза и факта равен нулю, только когда они оба равны нулю. В таком случае получается, что мы спрогнозировали отсутствие спроса, и его, действительно, не было – то есть ошибка тоже равна нулю – мы сделали совершенно точное предсказание.   

Визуальный метод – графический

Визуальный метод состоит в том, что мы на график выводим значение прогнозной модели и факта продаж по тем моделям, которые хотим сравнить. Далее  сравниваем визуально, насколько прогнозная модель близка к фактическим продажам. Давайте рассмотрим на примере. В таблице представлены две прогнозные модели, а также фактические продажи по этому товару за тот же период. Для наглядности мы также рассчитали ошибку прогнозирования по обеим моделям.  

По графикам очевидно, что модель 2 описывает лучше продажи этого товара. Оценка ошибки прогнозирования тоже это показывает – 65% и 31% ошибка прогнозирования по модели 1 и модели 2 соответственно.

Недостатком данного метода является то, что небольшую разницу между моделями сложно выявить — разницу в несколько процентов сложно оценить по диаграмме. Однако эти несколько процентов могут существенно улучшить качество прогнозирования и планирования пополнения запасов в целом.  

Использование формул ошибки прогнозирования на практике

Практический аспект оценки ошибки прогнозирования я вывела отдельным пунктом. Это связано с тем, что все статистические методы расчета показателя ошибки прогнозирования рассчитывают то, насколько мы ошиблись в прогнозе в количественных показателях. Давайте теперь обсудим, насколько такой показатель будет полезен в вопросах управления запасами. Дело в том, что основная цель управления запасами  — обеспечить продажи, спрос наших клиентов. И, в конечном счете, максимизировать доход и прибыль компании. А эти показатели оцениваются как раз  в стоимостном выражении. Таким образом, нам важно при оценке ошибки прогнозирования понимать какой вклад каждая позиция внесла в объем продаж в стоимостном выражении. Когда мы оцениваем ошибку прогнозирования в количественном выражении мы предполагаем, что каждый товар имеет одинаковый вес в общем объеме продаж, но на самом деле это не так – есть очень дорогие товары, есть товары, которые продаются в большом количестве, наша группа А, а есть не очень дорогие товары, есть товары которые вносят небольшой вклад в объем продаж. Другими словами большая ошибка прогнозирования по товарам группы А будет нам «стоить» дороже, чем низкая ошибка прогнозирования по товарам группы С, например. Для того, чтобы наша оценка ошибки прогнозирования была корректной, релевантной целям управления запасами, нам необходимо оценивать ошибку прогнозирования по всем товарам или по отдельной группе не по средними показателями, а средневзвешенными с учетом прогноза и факта в стоимостном выражении.

Пример расчета такой оценки Вы сможете увидеть в файле Excel.

Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>

При этом нужно помнить, что для оценки ошибки прогнозирования по отдельным позициям мы рассчитываем по количеству, но вот если нам важно понять в целом ошибку прогнозирования по компании, например, для оценки модели, которую используем, то нам нужно рассчитывать не среднюю оценку по всем товарам, а средневзвешенную с учетом стоимостной оценки. Оценку можно брать по ценам себестоимости или ценам продажи, это не играет большой роли, главное, эти же цены (тип цен) использовать при всех расчетах.  

Для чего используется ошибка прогнозирования

В первую очередь, оценка ошибки прогнозирования нам необходима для оценки того, насколько мы ошибаемся при планировании продаж, а значит при планировании поставок товаров. Если мы все время прогнозируем продажи значительно больше, чем потом фактически продаем, то вероятнее всего у нас будет излишки товаров, и это невыгодно компании. В случае, когда мы ошибаемся в обратную сторону – прогнозируем продажи меньше чем фактические продажи, с большой вероятностью у нас будут дефициты и компания не дополучит прибыль. В этом случае ошибка прогнозирования служит индикатором качества планирования и качества управления запасами.

Индикатором того, что повышение эффективности возможно за счет улучшения качества прогнозирования. За счет чего можно улучшить качество прогнозирования мы не будем здесь рассматривать, но одним из вариантов является поиск другой модели прогнозирования, изменения параметров расчета, но вот насколько новая модель будет лучше, как раз поможет показатель ошибки прогнозирования или точности прогноза. Сравнение этих показателей по нескольким моделям поможет определить ту модель, которая дает лучше результат.

В идеальном случае, мы можем так подбирать модель для каждой отдельной позиции. В этом случае мы будем рассчитывать прогноз по разным товарам по разным моделям, по тем, которые дают наилучший вариант именно для конкретного товара.

Также этот показатель можно использовать при выборе автоматизированного инструмента для прогнозирования спроса и управления запасами. Вы можете сделать тестовые расчеты прогноза в предлагаемой программе и сравнить ошибку прогнозирования полученного прогноза с той, которая есть у вашей существующей модели. Если у предлагаемого инструмента ошибка прогнозирования меньше. Значит, этот инструмент можно рассматривать для применения в компании. Кроме этого, показатель точности прогноза или ошибки прогнозирования можно использовать как KPI сотрудников, которые отвечают за подготовку прогноза продаж или менеджеров по закупкам, в том случае, если они рассчитывают прогноз будущих продаж при расчете заказа.

Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>

Если вы хотите повысить эффективность управления запасами и увеличить оборачиваемость товарных запасов, предлагаю изучить мастер-класс «Как увеличить оборачиваемость товарных запасов».

Источник: сайт http://uppravuk.net/