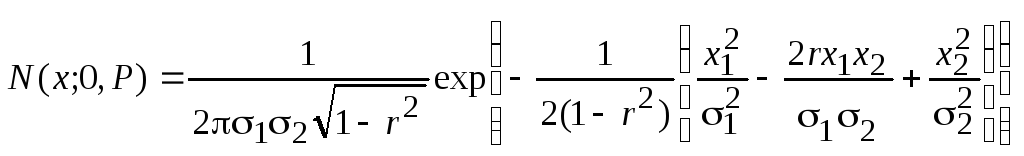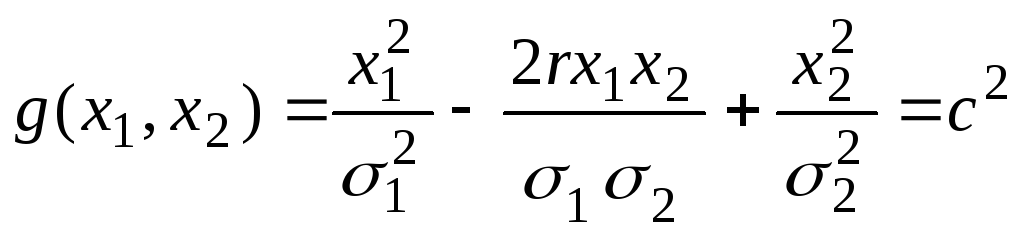Вероятность круговой ошибки

From Wikipedia, the free encyclopedia

In the military science of ballistics, circular error probable (CEP)^[1] (also circular error probability^[2] or circle of equal probability^[3]) is a measure of a weapon system’s precision. It is defined as the radius of a circle, centered on the mean, whose perimeter is expected to include the landing points of 50% of the rounds; said otherwise, it is the median error radius.^[4][5] That is, if a given munitions design has a CEP of 100 m, when 100 munitions are targeted at the same point, 50 will fall within a circle with a radius of 100 m around their average impact point. (The distance between the target point and the average impact point is referred to as bias.)

There are associated concepts, such as the DRMS (distance root mean square), which is the square root of the average squared distance error, and R95, which is the radius of the circle where 95% of the values would fall in.

The concept of CEP also plays a role when measuring the accuracy of a position obtained by a navigation system, such as GPS or older systems such as LORAN and Loran-C.

Concept[edit]

The original concept of CEP was based on a circular bivariate normal distribution (CBN) with CEP as a parameter of the CBN just as μ and σ are parameters of the normal distribution. Munitions with this distribution behavior tend to cluster around the mean impact point, with most reasonably close, progressively fewer and fewer further away, and very few at long distance. That is, if CEP is n metres, 50% of shots land within n metres of the mean impact, 43.7% between n and 2n, and 6.1% between 2n and 3n metres, and the proportion of shots that land farther than three times the CEP from the mean is only 0.2%.

CEP is not a good measure of accuracy when this distribution behavior is not met. Precision-guided munitions generally have more «close misses» and so are not normally distributed. Munitions may also have larger standard deviation of range errors than the standard deviation of azimuth (deflection) errors, resulting in an elliptical confidence region. Munition samples may not be exactly on target, that is, the mean vector will not be (0,0). This is referred to as bias.

To incorporate accuracy into the CEP concept in these conditions, CEP can be defined as the square root of the mean square error (MSE). The MSE will be the sum of the variance of the range error plus the variance of the azimuth error plus the covariance of the range error with the azimuth error plus the square of the bias. Thus the MSE results from pooling all these sources of error, geometrically corresponding to radius of a circle within which 50% of rounds will land.

Several methods have been introduced to estimate CEP from shot data. Included in these methods are the plug-in approach of Blischke and Halpin (1966), the Bayesian approach of Spall and Maryak (1992), and the maximum likelihood approach of Winkler and Bickert (2012). The Spall and Maryak approach applies when the shot data represent a mixture of different projectile characteristics (e.g., shots from multiple munitions types or from multiple locations directed at one target).

Conversion[edit]

While 50% is a very common definition for CEP, the circle dimension can be defined for percentages. Percentiles can be determined by recognizing that the horizontal position error is defined by a 2D vector which components are two orthogonal Gaussian random variables (one for each axis), assumed uncorrelated, each having a standard deviation . The distance error is the magnitude of that vector; it is a property of 2D Gaussian vectors that the magnitude follows the Rayleigh distribution, with a standard deviation , called the distance root mean square (DRMS). In turn, the properties of the Rayleigh distribution are that its percentile at level is given by the following formula:

or, expressed in terms of the DRMS:

The relation between and are given by the following table, where the values for DRMS and 2DRMS (twice the distance root mean square) are specific to the Rayleigh distribution and are found numerically, while the CEP, R95 (95% radius) and R99.7 (99.7% radius) values are defined based on the 68–95–99.7 rule

Measure of	Probability
DRMS	63.213…
CEP	50
2DRMS	98.169…
R95	95
R99.7	99.7

We can then derive a conversion table to convert values expressed for one percentile level, to another.^[6][7] Said conversion table, giving the coefficients to convert into , is given by:

From to	RMS ()	CEP	DRMS	R95	2DRMS	R99.7
RMS ()	1.00	1.18	1.41	2.45	2.83	3.41
CEP	0.849	1.00	1.20	2.08	2.40	2.90
DRMS	0.707	0.833	1.00	1.73	2.00	2.41
R95	0.409	0.481	0.578	1.00	1.16	1.39
2DRMS	0.354	0.416	0.500	0.865	1.00	1.21
R99.7	0.293	0.345	0.415	0.718	0.830	1.00

For example, a GPS receiver having a 1.25 m DRMS will have a 1.25 m × 1.73 = 2.16 m 95% radius.

Warning: often, sensor datasheets or other publications state «RMS» values which in general, but not always,^[8] stand for «DRMS» values. Also, be wary of habits coming from properties of a 1D normal distribution, such as the 68-95-99.7 rule, in essence trying to say that «R95 = 2DRMS». As shown above, these properties simply do not translate to the distance errors. Finally, mind that these values are obtained for a theoretical distribution; while generally being true for real data, these may be affected by other effects, which the model does not represent.

See also[edit]

• Probable error

References[edit]

Further reading[edit]

External links[edit]

• Circular Error Probable in Ballistipedia

В военной науке о баллистике , круговое вероятное отклонение ( СЕР ) (также круговое вероятное отклонение или круг равновероятно ) является мерой системы оружейные в точности . Он определяется как радиус круга с центром в среднем, периметр которого, как ожидается, будет включать точки приземления 50% выстрелов ; иначе говоря, это средний радиус ошибки. То есть, если данная конструкция боеприпасов имеет КВО 100 м, когда 100 нацелены на одну и ту же точку, 50 попадут в круг с радиусом 100 м вокруг их средней точки удара. (Расстояние между целевой точкой и средней точкой удара называется смещением .)

Существуют связанные концепции, такие как DRMS ​​(среднеквадратическое значение расстояния), которое представляет собой квадратный корень из средней квадратичной ошибки расстояния, и R95, который представляет собой радиус круга, в который попадают 95% значений.

Концепция CEP также играет роль при измерении точности положения, полученного навигационной системой, такой как GPS, или более старыми системами, такими как LORAN и Loran-C .

Концепция

Первоначальная концепция CEP была основана на круговом двумерном нормальном распределении (CBN) с CEP в качестве параметра CBN, так же как μ и σ являются параметрами нормального распределения . Боеприпасы с таким характером распределения имеют тенденцию группироваться вокруг средней точки удара, причем наиболее близко, постепенно все меньше и меньше, и очень мало на большом расстоянии. То есть, если CEP составляет n метров, 50% выстрелов попадают в пределах n метров от среднего удара, 43,7% между n и 2n и 6,1% между 2n и 3n метрами, а доля выстрелов, которые попадают на расстояние более чем в три раза больше CEP от среднего составляет всего 0,2%.

CEP не является хорошим показателем точности, когда это поведение распределения не соблюдается. Боеприпасы с высокоточным наведением обычно имеют больше «попаданий в цель» и поэтому обычно не распространяются. Боеприпасы также могут иметь большее стандартное отклонение ошибок дальности, чем стандартное отклонение ошибок азимута (отклонения), что приводит к эллиптической доверительной области . Образцы боеприпасов могут не точно попадать в цель, то есть средний вектор не будет (0,0). Это называется предвзятостью .

Чтобы включить точность в концепцию CEP в этих условиях, CEP можно определить как квадратный корень из среднеквадратичной ошибки (MSE). MSE будет суммой дисперсии ошибки дальности плюс дисперсия ошибки азимута плюс ковариация ошибки дальности с ошибкой азимута плюс квадрат смещения. Таким образом, MSE результатов объединения всех этих источников ошибок, геометрический соответствующее радиус о наличии окружности , в течение которого 50% туров будет земля.

Было введено несколько методов для оценки CEP по данным выстрелов. В эти методы включены подключаемый подход Блишке и Халпина (1966), байесовский подход Сполла и Марьяка (1992) и подход максимального правдоподобия Винклера и Бикерта (2012). Подход Сполл и Марьяк применяется, когда данные о выстреле представляют собой смесь различных характеристик снаряда (например, выстрелы из нескольких типов боеприпасов или из нескольких мест, направленных на одну цель).

Преобразование

Хотя 50% — очень распространенное определение для CEP, размер круга может быть определен в процентах. Процентили можно определить, признав, что ошибка горизонтального положения определяется двумерным вектором, компоненты которого являются двумя ортогональными гауссовскими случайными величинами (по одной для каждой оси), предположительно некоррелированными , каждая из которых имеет стандартное отклонение . Ошибка расстояния является величиной этого вектора; свойство двумерных гауссовских векторов состоит в том, что величина соответствует распределению Рэлея со стандартным отклонением , называемым среднеквадратичным значением расстояния (DRMS). В свою очередь, свойства распределения Рэлея таковы, что его процентиль на уровне задается следующей формулой:

или в терминах DRMS:

Связь между и дана в следующей таблице, где значения DRMS ​​и 2DRMS (удвоенное среднеквадратичное значение расстояния) относятся к распределению Рэлея и находятся численно, а значения CEP, R95 (радиус 95%) и R99. 7 значений (радиус 99,7%) определены на основе правила 68–95–99,7.

Мера	Вероятность (%)
DRMS	63,213 …
CEP	50
2DRMS	98,169 …
R95	95
99,7 рэндов	99,7

Затем мы можем составить таблицу преобразования для преобразования значений, выраженных для одного уровня процентиля, в другой. Указанная таблица преобразования, давая коэффициенты для преобразования в , определяется по формуле:

От до	RMS ( )	CEP	DRMS	R95	2DRMS	99,7 рэндов
RMS ( )	1	1,1774	1,4142	2,4477	2,8284	3,4086
CEP	0,8493	1	1.2011	2,0789	2,4022	2,8950
DRMS	0,7071	0,8326	1	1,7308	2	2,4103
R95	0,4085	0,4810	0,5778	1	1,1555	1,3926
2DRMS	0,3536	0,4163	0,5	0,8654	1	1,2051
99,7 рэндов	0,2934	0,3454	0,4149	0,7181	0,8298	1

Например, приемник GPS с DRMS ​​1,25 м будет иметь радиус 1,25 м 1,73 = 2,16 м 95%.

Предупреждение: часто в технических описаниях датчиков или в других публикациях указываются значения «RMS», которые в целом, но не всегда , соответствуют значениям «DRMS». Также будьте осторожны с привычками, проистекающими из свойств одномерного нормального распределения , таких как правило 68-95-99.7 , по сути пытаясь сказать, что «R95 = 2DRMS». Как показано выше, эти свойства просто не влияют на ошибки расстояния. Наконец, помните, что эти значения получены для теоретического распределения; хотя в целом это справедливо для реальных данных, на них могут влиять другие эффекты, которые модель не отражает.

Смотрите также

• Вероятная ошибка

использованная литература

дальнейшее чтение

внешние ссылки

• Вероятность круговой ошибки в Ballistipedia

Среднеквадратический эллипс ошибок, круговая вероятная ошибка

Проанализируем
более подробно характеристики,
используемые для описания свойств
двухмерных гауссовских векторов.
Двухмерный случай весьма важен в задачах
обработки статистической информации.
Так, при решении навигационных задач
на плоскости нередко полагают, что
координаты объекта представляют собой
гауссовский случайный вектор с
математическим ожиданием в точке его
предполагаемого местонахождения. Для
описания неопределенности расположения
точки на плоскости используют введенные
выше эллипсы равных вероятностей, в
частности эллипс, соответствующий
уравнению (3.35) при
.
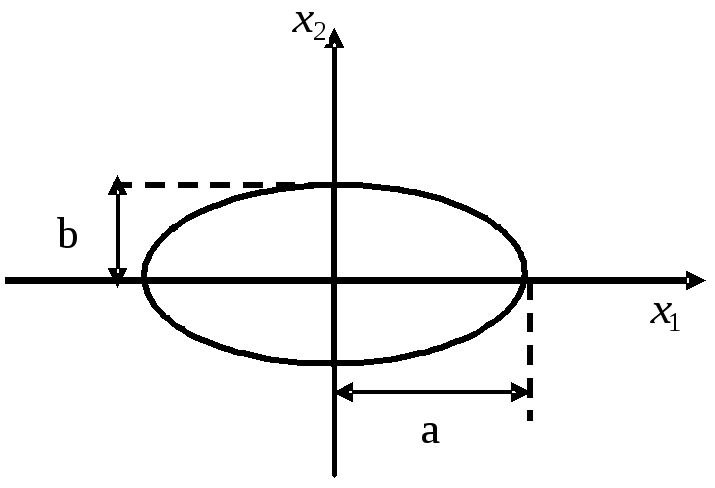
Поскольку этот эллипс пересекает оси
в точках, совпадающих со значениями
соответствующих СКО, т.е. при,
а при,
он получил наименованиесреднеквадратического
эллипса ошибок, или стандартного эллипса
[23]. В
навигационных приложениях для его
описания используют параметры
эллипса:
большую
ималую
полуоси
и дирекционный
угол
,
задающий ориентацию большой полуоси
относительно оси.
Эти три параметра полностью определяют
матрицу ковариаций двухмерной гауссовской
плотности. На рис. 3.4 изображен частный
случай, когда,
,
,
и таким
образом

, (3.36)

т.е. размеры полуосей
эллипса определяют значения СКО по
каждой координате.

Рис.
1.2.4. Эллипс ошибок для двухмерного
гауссовского вектора

с независимыми
компонентами

При оценивании
точности местоположения подвижных
объектов весьма важным представляется
умение охарактеризовать неопределенность
местоположения одним
числом. Для
этих целей обычно используют значения
вероятности
попадания
точки на плоскости в ту или иную заданную
область
.
Для двухмерного центрированного
гауссовского вектора с плотностью

эта вероятность
определяется как

, (3.37)

Если в качестве
выступает область, ограниченная

то, переходя к
полярным координатам, можно показать,
что [44, с. 68]

. (3.38)

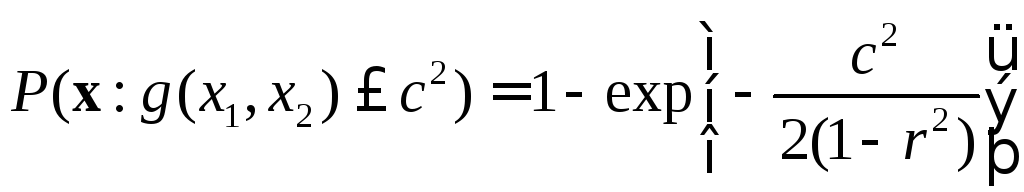
Для случая
независимых случайных величин при
эллипс превращается в окружность
радиусоми, таким образом, из (3.38) получаем, что
вероятность нахождения случайного
вектора в круге с таким радиусом
определяется введенным в разделе 2
распределением Рэлея

,
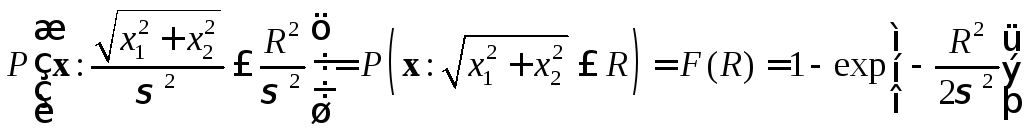
R>0. (1.39)

Круговая вероятная
ошибка (КВО).
Величина
,
соответствующая 50-процентному попаданию
гауссовского случайного вектора в круг
заданного радиуса, т.е. когда вероятность
попадания равна 0,5, называетсякруговой
вероятной ошибкой (КВО),
а круг, соответственно, кругом
равных вероятностей.
В англоязычной литературе для круговой
вероятной ошибки используется термин
circular error
probable (CEP).

Отметим, что для
независимых
случайных величин с равными
СКО

,
50-процентное попадание в круг (P=0,5)
достигается при
1,177.
Для круга радиуса
обеспечивается попадание с вероятностьюP=0,997.
В случае если
радиус круга, при котором достигается
вероятность попадания в него, равная
0,5, либо другой вероятности следует
отыскивать с помощью соотношения (3.37).

Радиальная
среднеквадратическая ошибка (Distance
Root Mean Square (DRMS)

Эта ошибка
определяется как

. (3.40)

Отметим, что
вероятность попадания в круг такого
радиуса составляет величину 0.65-0.68 в
зависимости от значений параметров
эллипса рассеивания.

Удвоенная
радиальная среднеквадратическая ошибка
(2DRMS).

Вероятность
попадания в круг такого удвоенного
радиуса зависит от конкретных соотношений
СКО и коэффициента корреляции, а примерная
ее величина определяется как P=0,95.

Понятия, аналогичные
приведенным выше, используются и для
трехмерного гауссовского вектора. При
этом вводится величина сферической
вероятной ошибки (СВО)
и сферы равных
вероятностей
(spherical error
probable (SEP)
и sphere of equal
probability (SEP)). Трехмерное
гауссовское распределение широко
используется при описании ошибок
местоположения подвижных объектов в
пространстве, в частности для летательных
аппаратов.

Соседние файлы в папке Кафедра ТВ

• #
• #
• #
• #
• #
• #

Концепция CEP также вступает в игру, когда речь идет об измерении подходящей точности определения местоположения, обеспечиваемой вашей навигационной системой, такой как GPS или люди. системы, такие как LORAN и Loran-C.

Концепция

Основное правило CEP было основано на круговом двумерном нормальном распределении (CBN), где CEP был параметром самого CBN , поскольку μ и σ являются параметрами, близкими к нормальному распределению. Боеприпасы с этой дозировкой имеют тенденцию концентрироваться вокруг намеченной точки вместе с ударом, и большинство из них вполне приличные, достигают меньше и очень мало при длинных вращениях вокруг блока. Другими словами, если CEP составляет t метров, 50% выстрелов находятся в пределах химических метров удара, 43,7% находятся между n и, следовательно, 2n, 6,1% находятся между 2n и 3n садами, а доля выстрелов, приземляющихся на открытом воздухе, места при ударе. . CEP более чем в четыре раза по сравнению со средним повышенным значением, составляющим всего 0,2%.

CEP не всегда так хорош в измерении точности, если это поведение отправки нарушено. Высокоточные боеприпасы традиционно больше промахиваются в непосредственной близости и не могут нормально разнестись. Боеприпасы также могут иметь стандартную разность ошибок по дальности, превышающую стандартное отклонение единицы измерения, вместе с ошибками азимута (отклонения), что приводит к эллиптическому падению критического времени. Образцы боеприпасов могут быть неточными для данной крупной цели, т. е. средний вектор точно не будет (0,0). Это называется предрасположенностью.

Чтобы улучшить внешний вид точности расчета CEP в таких условиях, CEP может быть выражен как, я бы сказал, квадратный корень из ожидаемого квадрата недосмотра (MSE). MSE всегда является суммой общей дисперсии ошибки дальности плюс модель ошибки азимута плюс ковариация главы ошибки дальности с ошибкой азимута плюс квадрат относительно смещения. Таким образом, MSE является явно конкретным результатом суммирования всех этих прерывистых режимов, геометрически в пределах соответствующего радиуса круга, где будет найдено 50% случаев.

Введено несколько методов оценки CEP на основе данных выстрелов. Эти методы включали своего рода подключаемый подход Блишке и Халпина (1966), своего рода байесовский выбор Сполла и Марьяка (1992) в сочетании с общим подходом максимального правдоподобия Винклера в дополнение к Бикерту (2012). Подход Сполла и Маржака действительно используется, когда данные выстрела представляют собой смесь различных свойств снаряда (например, выстрелы с использованием двойных типов боеприпасов или выстрелы из нескольких мест, направленные в цель).

Конверсия

Хотя 50% может быть обычным определением CEP, размер кольца можно указать в процентах. Процентили можно определить, признав, что каждая ошибка горизонтального расположения определяется двумерным действительным вектором, компоненты которого являются более чем двумя ортогональными гауссовскими целевыми переменными. Поскольку (по одному на каждой отдельной оси), когда и если они не коррелированы, каждый из них по умолчанию имеет огромную большую разницу . Ошибка расстояния может быть величиной вместе с этим вектором; На самом деле это свойство двумерных гауссовских векторов любого размера, которое подходит для распределения Рэлея одной стандартной редакции определяется по следующей формуле:

Круговое вероятное отклонение (КВО) — показатель точности попадания бомбы, ракеты, снаряда, применяемый для оценки вероятности поражения цели. Круговое рассеивание является частным случаем более общего понятия вероятного или срединного отклонения, широко используемого в артиллерийской практике и баллистике с XIX века. Как характеристика эффективности ракетного оружия КВО или по англ. CEP (от circular error probable) введено в оборот в специальной технической литературе в конце 1940-х — начале 1950-х годов.

КВО выражается величиной радиуса круга, очерченного вокруг цели, в который предположительно должно попасть 50 % боеприпасов (или их боевых частей); далее для простоты они будут называться снарядами.

По определению, если КВО равно L, то 50 % снарядов падает на расстояниях от цели меньших либо равных L. Если при этом места падения снарядов подчиняются некоррелированному двумерному нормальному распределению с равными стандартными отклонениями σx = σy = σ по обеим осям (часто встречающийся в практике случай, см. рис. 2), то примерно 43,7 % снарядов падают на расстояниях между L и 2L от цели, около 6,1 % — на расстояниях между 2L и 3L, и лишь 0,2 % снарядов падает на расстояниях от цели, больших, чем три величины КВО. Стандартное отклонение по любой горизонтальной оси σ связано с КВО соотношением L = σ·√2 ln 2 ≈ 1,1774 σ. Для кругового нормального распределения расстояние от точки падения снаряда до цели (промах, s) подчиняется распределению Рэлея. При этом максимум плотности кругового распределения вероятностей находится в точке цели, однако среднеквадратичный промах равен srms = σ·√2 ≈ 1,2011L (внутрь круга с таким радиусом попадает 63,213% снарядов, а в круг с удвоенным радиусом 2srms ≈ 2,4022L — 98,169% снарядов). Применительно к круговому нормальному распределению часто встречается также величина R95 ≈ 2,4477 σ ≈ 2,0789 L — радиус круга с центром в цели, в который попадает 95% снарядов.

На практике распределение попаданий относительно точки прицеливания может не подчиняться круговому нормальному закону. В частности, применительно к высокоточному оружию отмечается группирование точек падения ближе к условному центру рассеивания, и, таким образом, имеет место отклонение от нормального распределения. Для артиллерийских боеприпасов при стрельбе по целям на горизонтальной поверхности характерны увеличенные значения вероятного отклонения по дальности по сравнению с вероятным отклонением в боковом направлении, с образованием доверительной области в форме эллипса (эллипс рассеивания), вытянутого по дальности. В этом случае соотношения, указанные выше, недействительны, однако концепция КВО всё ещё может использоваться, оставаясь мерой точности стрельбы (меньшее значение КВО соответствует лучшей точности стрельбы).

С увеличением дальности достижение малого КВО становится всё более трудной задачей.

Точность главным образом зависит от степени совершенства систем наведения (для управляемых боеприпасов — также и систем управления), а также от аэродинамических показателей.

Современные крылатые ракеты и управляемые (корректируемые) авиабомбы имеют КВО, не превышающее 10 метров. Самые точные баллистические ракеты имеют КВО менее 100 метров, даже при межконтинентальных дальностях. У первой баллистической ракеты «Фау-2» (V2), созданной в 1942 году и имевшей практическую дальность полёта около 250—270 километров (максимально — 320 км), КВО составляло от 4,5 до 6 км.

Сравнение ракет по КВО

• UGM-133A Трайдент II (D5) — 90…500 м
• Р-30 Булава-30 — 120…350 м

В современной культуре

Термин КВО используется в фильме «Прямая и явная угроза», когда наземная группа сообщает «Вероятность круговой ошибки ноль. Удар при детонации высокого порядка. Хорошего дня». В данном случае параметр «КВО» используется для обозначения ситуации, что боезаряд попал точно в цель.