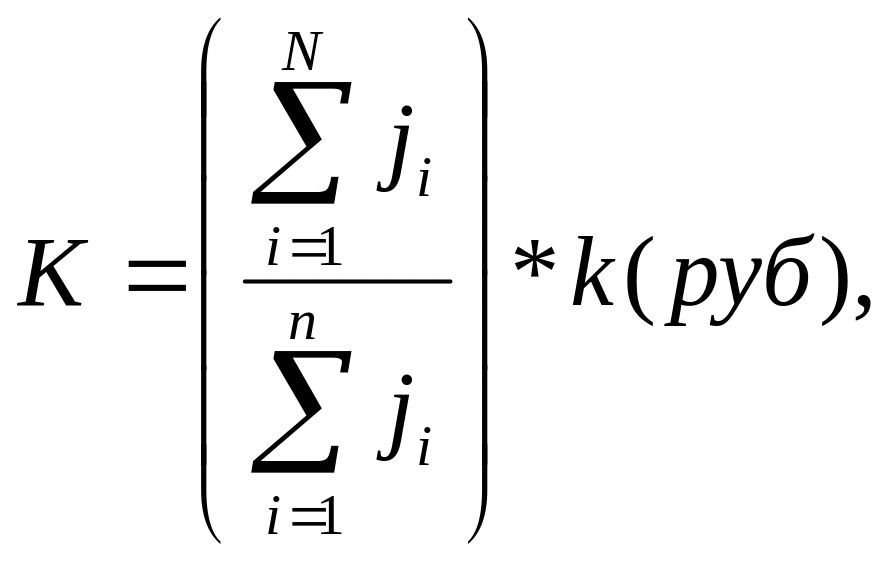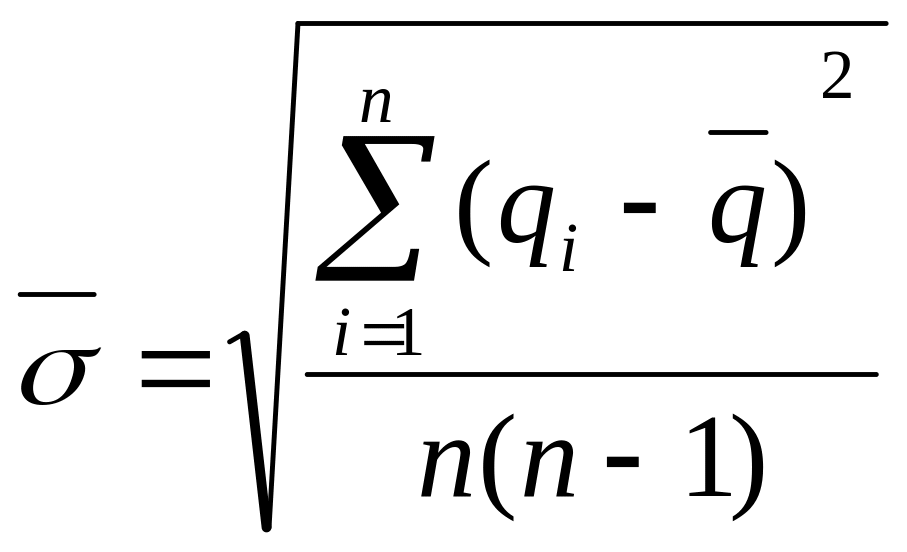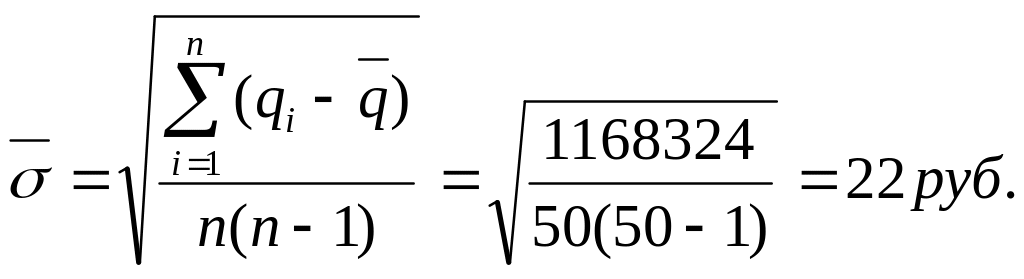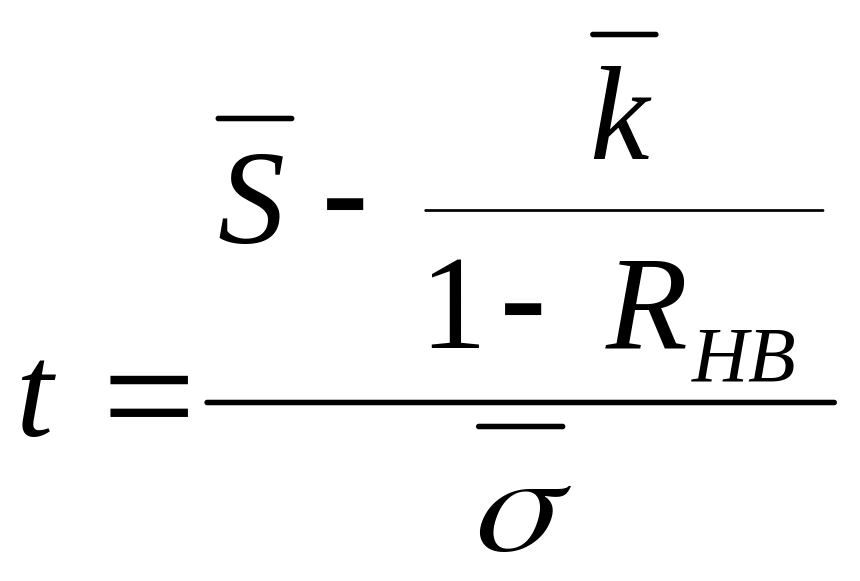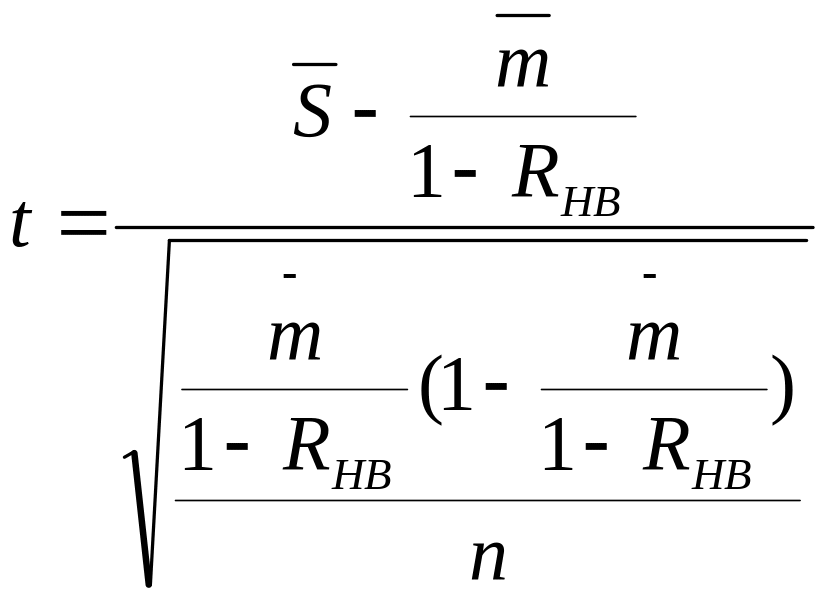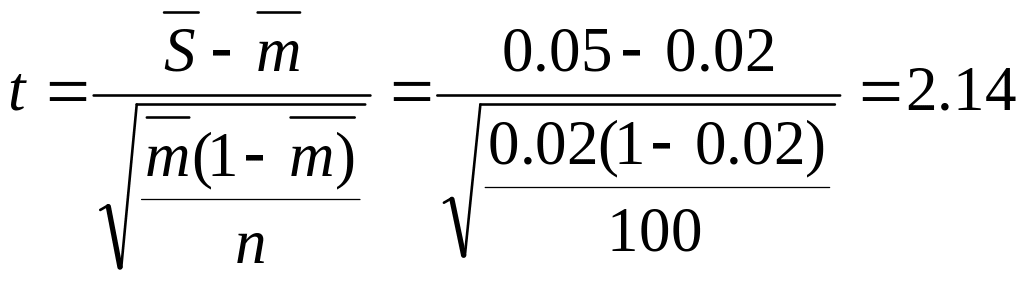Вероятность определения ожидаемой ошибки

Как мы отметили ранее, насущной задачей теории аудита является разработка и обоснование методов оценки вероятности определения ожидаемой ошибки (аудиторского риска).

Дело в том, что в любом случае, даже при сплошных проверках, не говоря уже о выборочных, определение ожидаемой ошибки содержит элемент случайности (аудитор мог не заметить ошибку, мог неправильно истолковать содержание хозяйственной операции и т. д.).

Следовательно, определение ожидаемой ошибки К всегда осуществляется с какой-то вероятностью (аудиторским риском).

В соответствии с требованиями международных и федеральных аудиторских стандартов аудитор обязан оценивать аудиторский риск и разрабатывать процедуры, необходимые для снижения риска до приемлемо низкого уровня.

Стандарты устанавливают также, что аудитор должен оценивать риск как на уровне отчетности в целом, так и на уровне сальдо по счетам (т. е. для отдельных статей баланса), а также на уровне групп однотипных операций (т. е. для оборотов по счетам бухгалтерского учета).

Для осуществления требуемых оценок необходимо определить аудиторский риск и уяснить для себя его природу.

Стандарты определяют аудиторский риск как возможность выражения аудитором ошибочного мнения, в то время как в бухгалтерской отчетности будут содержаться существенные ошибки, искажения.

Это – концептуальное определение, малопригодное для практической работы. Дадим более строгое определение аудиторского риска.

Для этого введем следующие обозначения: S (руб.) – уровень существенности базового показателя (статьи бухгалтерской отчетности); К (руб.) – ожидаемая (наиболее вероятная) ошибка, которая, по мнению аудитора, содержится в статье бухгалтерской отчетности, для которой установлен уровень существенности S; Q (руб.) – действительная ошибка, содержащаяся в данной статье бухгалтерской отчетности.

Тогда аудиторский риск на уровне отчетности в целом – это вероятность события, заключающаяся в том, что хотя бы для одной статьи бухгалтерской отчетности выполняется неравенство K < S при выполнении неравенства Q > S (ожидаемая ошибка меньше уровня существенности, в то время как действительная ошибка превышает его).

Аудиторский риск на уровне оборота по конкретному счету (генеральной совокупности операций) – это вероятность события, заключающегося в том, что неравенства K < S при Q > S выполняются для генеральной совокупности операций, составляющей оборот (дебетовый или кредитовый) данного счета (в этом случае S, K, Q – уровень существенности, ожидаемая ошибка и действительная ошибка для оборота рассматриваемого счета).

Итак, согласно нашему определению аудиторский риск – это вероятность наступления некоего события. Вероятность есть величина математическая, и она может быть определена количественно (в долях единицы либо процентах).

Указанные выше стандарты предусматривают также возможность качественной оценки, исходя, по крайней мере, из трех градаций (низкий риск, средний риск, высокий риск).

Для того чтобы обоснованно выбрать способ оценки, надо уяснить себе природу аудиторского риска.

Очевидно, что аудиторский риск для отчетности в целом, равно как и аудиторский риск на уровне сальдо и оборотов по счетам при применении процедур сплошной проверки, либо выборочных процедур, основанных на нестатистических (содержательных) методах, – это субъективная вероятность, т. е. вероятность, основанная не на статистическом или классическом ее определении, а на суждении экспертов (аудиторов), учитывающих имеющийся опыт, влияние различных факторов и т. д.

Если же говорить об аудиторском риске на уровне сальдо и оборотов по счетам при применении выборочных процедур, основанных на статистических методах, то в этом случае аудиторский риск – это статистическая вероятность, которая может быть численно определена исходя из закона распределения случайной величины (размера ошибок либо количества ошибок в выборке).

Как мы отметили
ранее, применение статистических
выборочных методов определения ожидаемой
ошибки К, рассмотренных в предыдущих
разделах, оправдано не во всех случаях,
а лишь тогда, когда объем генеральных
совокупностей достаточно велик (сотни,
тысячи элементов), а ошибки случайны и
равновозможны.

Если объем
генеральной совокупности невелик
(например, не более нескольких десятков
документов), то проведение сплошной
проверки займет у аудитора меньше
времени, чем обработка результатов
выборочного исследования. Отметим, что
при сплошной проверке аудитор
непосредственно определяет ожидаемую
ошибку К как сумму всех выявленных им
в проверяемой совокупности ошибок.

В другом случае
объем генеральной совокупности может
быть слишком велик для сплошной проверки
(например, не менее нескольких сотен
документов). Но при этом у аудитора может
иметься информация (источники появления
ее будут рассмотрены позднее), исключающая
применимость предположения о
равновозможности и случайности ошибок
в генеральной совокупности. В таком
случае оправдано применение содержательных
методов выборочного исследования.
Содержательные методы, как следует из
их названия, основаны на содержании
имеющейся у аудитора информации о
характере распределения ошибок в
генеральной совокупности.

Рассмотрим
возможные причины неслучайности и
неравновозможности ошибок в генеральных
совокупностях.

Очевидно, что
ошибки неслучайны, если они появляются
в силу какой-то постоянно действующей
причины (в этом случае ошибки будут
систематическими). Причиной появления
систематических ошибок чаще всего
бывает слабое знание (незнание) либо
неправильное, недостаточное понимание
бухгалтером законодательных и нормативных
актов Российской Федерации в области
учета налогообложения, хозяйственного
права. Другой причиной появления
систематических ошибок может быть
давление на бухгалтера со стороны
руководства организации.

Ошибки
неравновозможны, если в бухгалтерских
документах имеются учетные области, в
которых вероятность появления ошибок
значительно выше, чем в других. Такие
области (области с повышенной вероятностью
появления ошибок) будем называть
значимыми для аудита областями. Практика
показывает, что значимые для аудита
области могут иметь место, например, в
следующих случаях:

—
резкая неоднородность генеральной
совокупности — наличие в совокупности
документов, стоимость которых на порядок
(порядки) превышает стоимость большей
части документов (сосредоточение
значительных денежных сумм в небольшом
количестве документов нарушает
равновозможность появления ошибок);

—
появление в учете новых, ранее в данной
организации не встречавшихся хозяйственных
операций, вызванных, например, освоением
нового вида деятельности;

—
наличие в учете операций, неоднозначно
трактуемых законодательством, нормативными
актами, профессиональными комментаторами;

—
изменение правил учета и налогообложения
каких-либо операций (такие операции
будут составлять значимую область).

—
наличие в учёте операций со связанными
сторонами (при совершении подобных
операций возможны нарушения, обусловленные
взаимным интересом сторон и их особыми
отношениями друг с другом);

—
наличие в учёте операций с существенными
суммами по выполнению работ, оказанию
услуг, не имеющих вещественного результата
(консультации, информационные услуги,
обслуживание оборудования и т.д.);

—
наличие в учёте различных по сути
(подлежащих отнесению в связи с этим на
различные источники), но весьма близких
по своему содержанию операций и т.д.

Причины появления
значимых для аудита областей определяют
возможности содержательных выборочных
методов определения ожидаемой ошибки.
При этом следует иметь в виду, что
возможные причины появления значимых
для аудита областей, безусловно, не
ограничиваются приведенными выше
примерами, число их неисчерпаемо.

Поэтому, если
статистических методов, рассмотренных
выше, в общем-то, два, то содержательных
методов, наверное, столько же, сколько
практикующих аудиторов. Некоторые
аудиторы, проводя проверку, не задумываются
о методах (как не задумывался г-н Журден
о том, что он говорит прозой), а
руководствуются при осуществлении
выборки исключительно своим опытом и
интуицией, и при этом достигают отличных
результатов. Очевидно, происходит это
потому, что они неосознанно используют
эти самые содержательные методы.

Серьезного
научного обоснования содержательных
методов выборочного исследования в
аудите на сегодняшний день пока нет.
Тем не менее, некоторые общие принципы,
заложенные в основу содержательных
методов, хорошо себя зарекомендовали
на практике [6], и потому некоторые из
них могут быть рекомендованы для
практического использования. К подобным
методам выборочного исследования могут
быть отнесены следующие:

— метод,
основанный на блочном отборе документов
(метод «блочного отбора»);

— метод,
основанный на отборе документов
наибольшей стоимости (метод «основного
массива»);

— метод,
основанный на отборе документов, в
которых наличие ошибок наиболее вероятно,
либо в которых возникновение ошибок и
нарушений может вызвать наиболее
негативные для предприятия последствия
(метод «ключевых» элементов);

-комбинированный
метод, основанный на различных сочетаниях
вышеперечисленных методов.

Рассмотрим
содержание и практическое применение
указанных выше методов.

Метод «блочного
отбора»
заключается в формировании выборки
путем отбора из генеральной совокупности
«блока» документов – совокупности,
относящейся к определенному периоду
(например, документы за один месяц).

Ожидаемая
ошибка К генеральной совокупности
определяется при этом, как произведение
суммарной ошибки выборки на отношение
объемов генеральной совокупности и
выборки:

К = N
/ n

k
(руб.)
, (3.17)

где К (руб.) —
ожидаемая ошибка генеральной совокупности;
N (в натуральных единицах) – объем
генеральной совокупности; n (в натуральных
единицах) – объем выборки; k (руб.) —
суммарная ошибка в выборке.

Подобный прием
оправдан в тех случаях, когда в генеральной
совокупности преобладают систематические
ошибки, что исключает возможность
применения статистических методов.

Пример.
Аудитор проверяет кредитовый оборот
счета 02 — амортизацию основных средств,
начисленную в течение года. Объем
генеральной совокупности N = 1200 операций
(по 100 операций ежемесячно). В течение
года не было движения (выбытия или
оприходования) основных средств.
Соответственно, ежемесячная сумма
начисленной амортизации одна и та же.
Исходя из этого, аудитор предполагает,
что если генеральная совокупность
содержит ошибки, то исключительно
систематические, повторяющиеся ежемесячно
(например, неправильное применение
нормы амортизации). Аудитор выбирает
любой месяц и сплошным методом проверяет
начисление амортизации. Выявленная
ошибка k = 25 000 р. Поскольку объем выборки
n = 100 операций, то ожидаемая ошибка
генеральной совокупности

К = N
/ n

k
= 1200 / 100

25 000 = 300 000 р.

В зарубежной
литературе по аудиту содержатся указание
на то, что при методе «блочного отбора»
экстраполяция ошибки на генеральную
совокупность может осуществляться как
пропорционально соотношению объемов
генеральной и выборочной совокупностей
(N/n),
так и пропорционально соотношению их
стоимостей. Тогда ожидаемая ошибка
генеральной совокупности К будет
определяться из следующей зависимости:

(3.18)

где

— стоимость i-го
документа.

Численный
анализ, проведенный в работе [15], показал,
что при однородной стоимости элементов
генеральной совокупности (коэффициент
вариации менее 0,3) формулы (3.17) и (3.18) дают
практически равные результаты. При
большей неоднородности генеральной
совокупности формула (3.18) неприменима,
поскольку погрешность ее может быть
весьма значительной.

Метод «основного
массива»,
как следует из его названия, состоит в
том, что аудитор формирует выборку путем
отбора из генеральной совокупности
элементов наибольшей стоимости
(элементов, стоимость которых превышает
уровень существенности). Этот метод
оправдан в тех случаях, когда генеральная
совокупность неоднородна по стоимости
документов, составляющих ее: в совокупности
есть документы, стоимость которых на
порядок (порядки) превышает стоимость
бóльшей части документов. Опыт показывает,
что чаще всего количество подобных
документов в совокупностях невелико.
В литературе встречается даже «магическое»
соотношение: 20·80 (часто на 20% документов
приходится 80% стоимости всех документов
купности). Как отмечено ранее, применение
статистических методов в таком случае
неоправданно, так как сосредоточение
значительных денежных сумм в небольшом
количестве мест (документов) нарушает
принцип равновозможности — единственная
ошибка в документе, входящем в «основной
массив», сразу превышает уровень
существенности, в то время как в документах
«неосновного массива» для превышения
уровня существенности таких ошибок
должно быть, например, несколько десятков.

При применении
метода «основного массива» ожидаемая
ошибка генеральной совокупности К
принимается равной суммарной ошибке в
выборке k:

К=k
(руб). (3.19)

Теперь рассмотрим
метод «ключевых
элементов».
Метод состоит в формировании выборки
путем отбора элементов (операций), в
которых вероятность появления ошибок
значительно выше, чем в других (значимые
для аудита области), а также тех операций,
ошибки или нарушения в которых могут
вызвать существенный ущерб для
проверяемого субъекта, государства или
третьих лиц. Данные для осуществления
отбора могут быть основаны на опыте
предыдущих проверок, результатах
наблюдения и опроса, результатах
использования аналитических или
специальных процедур.

Как и в предыдущем
случае, ожидаемая ошибка генеральной
совокупности К принимается равной
суммарной ошибке в выборке k.

Пример.
Аудитор
проверяет дебетовый оборот счета 41 —
оприходование товара. Объем генеральной
совокупности N = 250 накладных. Из них 245
поставок — от постоянных российских
поставщиков, 5 поставок — от заграничных
поставщиков по импортным контрактам.
Причем ранее валютные операции проверяемым
предприятием не осуществлялись. Очевидно,
что 5 операций по импорту товара являются
как ключевыми по риску (вероятность
ошибок в непривычных операциях всегда
гораздо выше, чем в повседневных), так
и по последствиям (ошибки или нарушения
в валютных операциях могут повлечь
тяжелые последствия . Аудитор отбирает
5 операций импорта товара и проверяет
их сплошным образом.

Комбинированный
метод, как
следует из его названия, включает в себя
все вышеперечисленные методы в различных
сочетаниях. На практике чаще всего
применяется именно комбинированный
метод.

Пример.
Аудитор проверяет учет производственных
затрат (дебетовый оборот счета 20) на
малом предприятии. В состав производственных
затрат входят:

Генеральная
совокупность (операции, отраженные по
дебету счета 20) неоднородна по виду
операций, вследствие чего аудитор
стратифицирует ее на 5 совокупностей.

Совокупность
операций по ремонту (520 тыс. р.) аудитор
подвергает сплошной проверке в качестве
как «основного массива», так и «ключевых
элементов». Ожидаемая ошибка страты,
выявленная в ходе сплошной проверки,
составила К₁
= 4,5 тыс. р. (необоснованное отнесение на
счет 20).

Совокупность
операций по учету заработной платы с
начислениями (258 тыс. р.) аудитор подвергает
проверке методом «блочного отбора»,
полагая, что в ней преобладают
систематические ошибки. В качестве
блока аудитор выбирает документы за
один месяц. В ходе их проверки ошибок
не обнаружено,ожидаемая ошибка К₂
= 0.

Совокупность
операций по начислению амортизации (75
тыс. р.) аудитор из тех же соображений
подвергает «блочному отбору». В ходе
проверки документов за отобранный месяц
обнаружена ошибка в начислении амортизации
k = 500 р. Тогда ожидаемая ошибка страты

К₃
= N
/ n

k
= 12 / 1 · 500 = 6000 р.

Совокупность
операций по списанию материалов (185 тыс.
р.) содержит 450 операций. Аудитор подвергает
ее выборочной проверке с использованием
метода, основанного на нормальном
распределении. В ходе обработки
результатов выборочной проверки
получено: средняя ошибка выборки

= 20 р. Тогда ожидаемая ошибка страты

К₄
=

N
= 20

450 = 9 000 р.

Совокупность
операций по отнесению на затраты услуг
сторонних организаций (30 тыс. р.) аудитор
решает не проверять ввиду несущественности
ее суммы.

Тогда ожидаемая
ошибка генеральной совокупности:

К = К₁
+К₂
+К₃
+ К₄
= 4500 + 0 + 6000 + 9 000 = 19 500 р.

3.10.
Оценка аудиторского риска на уровне
сальдо и оборотов по

счетам

По результатам
применения аудиторских процедур,
рассмотренных выше, может быть оценен
аудиторский риск (его компоненты) на
уровне сальдо и оборотов по счетам, то
есть на уровне генеральных совокупностей,
в отношении которых применялись
аудиторские процедуры.

Рассмотрим эти
оценки.

3.10.1.
Оценка аудиторского риска при применении
выборочных

вероятностно-статистических
процедур

При применении
выборочных вероятностно-статистических
процедур аудиторский риск проявляет
себя как статистическая вероятность,
и может быть численно определен исходя
из закона распределения случайной
величины (размера ошибок, либо количества
ошибок в выборке).

Как известно
из статистики, при экстраполировании
результатов исследования репрезентативной
выборки на генеральную совокупность
вероятность определяется объёмом
выборки.

Упомянутая
статистическая вероятность при
репрезентативной выборке зависит только
от объема выборки, вследствие чего
согласно федеральному стандарту аудита
№ 16 «Аудиторская выборка» ее следует
определить, как риск выборки (риск,
связанный с объемом выборки – будем
обозначать его

).
Следует отметить, что наряду со
статистической вероятностью

при применении выборочных процедур,
основанных на вероятностно-статистических
методах, присутствует и субъективная
вероятность, которую стандарт № 16
определяет, как риск, не связанный с
объемом выборки (обозначим его

).
Этот риск зависит от прочих факторов,
не связанных с объемом выборки (опытом
и квалификацией аудитора, его
добросовестностью и пр.), и проявляет
себя в рассматриваемом случае, как
вероятность того, что аудитор может
обнаружить в выборке не все имеющиеся
в ней ошибки.

Таким образом,
аудиторский риск R_А
на уровне сальдо и оборотов по счетам
бухгалтерского учета при применении
выборочных процедур, основанных на
вероятностно- статистических методах,
является функцией двух компонентов —
риска выборки R_В
и риска, не связанного с выборкой R_НВ
:

R_А
= f (R_В,R_НВ).
(3.20)

Получим выражения
для риска выборки и аудиторского риска
применительно к известным
вероятностно-статистическим методам.

Сперва получим
выражение для риска выборки R_В
применительно к процедуре, основанной
на нормальном
распределении размера ошибок.

Риск
выборки R_В
является вероятностью события,
заключающегося в том, что действительная
ошибка Q
генеральной совокупности окажется
больше «применяемого» для данной
генеральной совокупности уровня
существенности S
, в то время, как полученная аудитором
ожидаемая ошибка К менее уровня
существенности (Q
S
при К
S).
Заметим, что неравенство К
S
может быть приведено к виду



,
где

— средний уровень существенности;

= K/N
– генеральная средняя; N
– объем генеральной совокупности.

Получим выражение
для риска выборки R_В.
Для этого вспомним, что при нормальном
распределении может быть определена
верхняя граница доверительного интервала

,
которую генеральная средняя

не должна превысить:


,
(3.21)

где

—
выборочная средняя;

— среднеквадратичная погрешность
выборочной средней; t
– предел
интеграла Лапласа..

Вероятность R
превышения генеральной средней

верхней границы доверительного интервала
a
будет являться риском выборки R_В
в том случае, когда верхняя граница
доверительного интервала будет равна
среднему уровню существенности (a=
).

Получаем следующее
выражение:

(3.22)

Среднеквадратичное
отклонение выборочной средней в выражении
для доверительного интервала подсчитывается
по известной зависимости:

.
(3.23)

где
n-
объем выборки; q_i
(руб.) –
размер ошибки в i-ом
элементе выборки.

Тогда
риск выборки R_В
может
быть найден из статистических таблиц
по значению t,
полученному из выражения для доверительного
интервала:

.
(3.24)

Таким
образом, для выборочной процедуры,
основанной на нормальном распределении
размера ошибки, риск выборки может быть
найден из зависимости

,
где значение предела интеграла Лапласа
t
определяется с помощью выражения (3.24).
Рассмотрим возможность применения
полученных зависимостей на примере.

Пример.
Воспользуемся
исходными данными примера, рассмотренного
ранее: объем
генеральной совокупности N=850
авансовых отчетов общей стоимостью
J=1 800 000
руб.; объем выборки n=50
авансовых отчетов; ошибки в авансовых
отчетах, попавших в выборку:

руб.
Уровень существенности установлен
аудитором в размере s=5%
( S
= 90 000 руб.). Определим ожидаемую ошибку
генеральной совокупности К и риск
выборки R_В.

Средняя ошибка
в выборке:

Ожидаемая
ошибка генеральной совокупности:

К=

*N=34*850=28 900
руб.

Среднеквадратичное
отклонение выборочной средней:

Средний уровень
существенности:

Расчетное
значение предела интеграла Лапласа:

Из
статистических таблиц [11] получаем, что
при t
=3,3 вероятность превышения генеральной
средней верхней границы доверительного
интервала равна 0,001. Таким образом, риск
выборки R_В
=0,1%. Из
этого следует, что с вероятностью 99,9%
ожидаемая ошибка генеральной совокупности
(наиболее вероятное значение которой
составляет 28 900 руб.) не превысит
уровень существенности, равный 90 000
руб.

Приведенные
выше рассуждения основаны на предположении
о том, что аудитор обнаружит в выборке
все ошибки q_i,
то есть на предположении о том, что риск
R_НВ,
определяемый опытом аудитора, его
информированностью о клиенте и т.д.,
равен нулю.

На
практике, конечно риск R_НВ
0,
поскольку аудитор в силу различных
причин (недостаток опыта, квалификации,
усталость, небрежность и т.д.) может
обнаружить не все ошибки в выборке.

Введём понятие
ошибки в выборке, обнаруженной аудитором
–

(руб.).

Вероятность
обнаружения аудитором всех ошибок в
выборке составит в таком случае

,
где

— средняя ошибка в выборке, обнаруженная
аудитором.

Поскольку эта
вероятность определяется всеми прочими
факторами (опыт и квалификация аудитора,
его добросовестность, знакомство с
проверяемой организацией и т.д.), то
вероятность противоположного события
– это риск R_НВ.
Тогда:

.
(3.25)

Из
выражения (3.14) получаем:

.
(3.26)

Риск
R_НВ
может быть численно оценен путем анализа
определяющих его указанных выше факторов,
например, как это показано выше, с помощью
линейной полиномиальной модели.

Тогда
аудиторский риск может быть определён
из статистических таблиц, как функция

,
где значение предела интеграла Лапласа
определяется из зависимости:

.
(3.27)

Пример. Используя
исходные данные предыдущего примера,
определим аудиторский риск, если
значение R_НВ
=35%.

Расчетное
значение предела интеграла Лапласа:

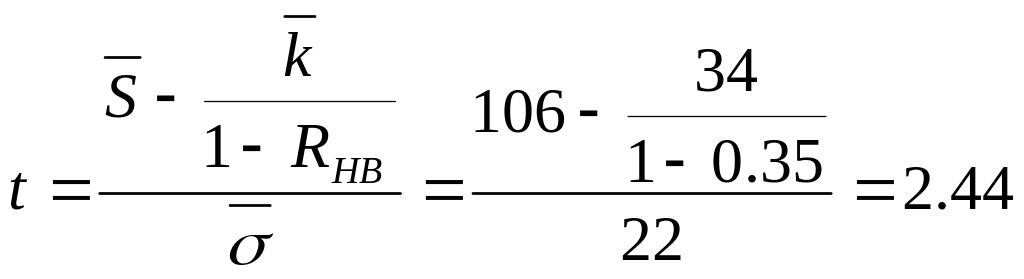
Из таблиц [11]
получаем, что при t
=2,44 аудиторский риск R_А
=0,005
(0,5%).

Теперь получим
выражение для риска выборки и аудиторского
риска применительно к процедуре,
основанной на биномиальном
распределении количества ошибок в
выборке.

Ведем следующие
обозначения: N
– объем генеральной совокупности; n
– объем выборки; m
– количество ошибок в выборке; M
– ожидаемая ошибка генеральной
совокупности (ожидаемое количество
ошибок в генеральной совокупности).

Как мы указали
ранее, в математической статистике
показано, что для биномиального
распределения наиболее вероятное
значение величины М определяется из
выражения M
= m*N/n.

В
[11] показано также, что для отношения
M/N
может быть определена верхняя граница
доверительного интервала a,
которую величина M/N
с вероятностью P
= 1 – R
не должна превысить:

,
(3.28)

где
t
– предел интеграла Лапласа;

— относительное количество ошибок в
выборке.

В
[11] указано, что формула (3.28) является
приближенной, но достаточной для
практических расчетов при значениях n
порядка сотен.

Приравняв верхнюю
границу доверительного интервала
среднему уровню существенности

,
(3.29)

получаем
значение предела интеграла Лапласа,
определяющее риск выборки R_В:

,
(3.30)

где

— средний уровень существенности.

Используя тот же
прием, что и при рассмотрении выборочной
процедуры, основанной на нормальном
распределении, получаем выражение для
предела интеграла Лапласа, определяющего
аудиторский риск:

.
(3.31)

Пример. Объем
генеральной совокупности N=2500
счетов-фактур. Объем выборки n
= 100 счетов- фактур. Количество ошибок
(неправильно заполненных счетов-фактур)
в выборке m
= 2. Уровень существенности S
=125 счетов- фактур (5%). Риск R_НВ
по
оценке аудитора составляет R_НВ
=20%.
Определим ожидаемую ошибку генеральной
совокупности М, риск выборки R_В
и
аудиторский риск R_А.

Относительное
количество ошибок в выборке:

.

Ожидаемая ошибка
генеральной совокупности:

M
= m*N/n
= 2* 2500/100 = 50 счетов-фактур.

Средний уровень
существенности:

.

Значение предела
интеграла Лапласа, определяющее риск
выборки:

.

При t
=2,14 риск выборки составляет R_В
=0,02
(2%).

Значение интеграла
Лапласа, определяющее аудиторский
риск:

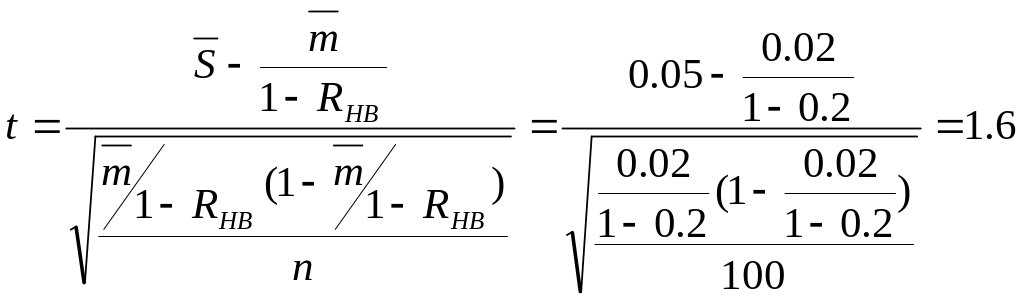
При t
= 1,6 аудиторский риск составляет R_А
=5,5%.

Итак, мы получили
выражения, с помощью которых можно
количественно оценить компоненту
аудиторского риска (риск выборки) как
статистическую вероятность при выборочных
проверках, основанных на нормальном
либо биномиальном законах распределения
случайных величин.

Но количественная
оценка риска выборки возможна ещё в
одном случае – при использовании
процедуры «основного массива». Покажем
это.