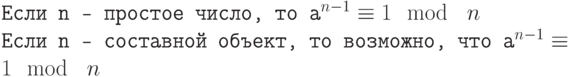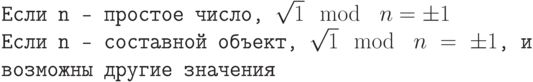Вероятность ошибки алгоритма

Случайность как вычислительный ресурс

Архив

Речь пойдет не о случайных действиях, а об алгоритмах, использующих случайность. Наряду с «обычными» действиями в вероятностном алгоритме разрешается «подбрасывание монетки», то есть использование случайных равномерно распределенных битов.

«Дело в том, что самые интересные и изящные научные результаты сплошь и рядом обладают свойством казаться непосвященным заумными и тоскливо-непонятными…»
А. и Б. Стругацкие.
«Понедельник начинается в субботу»

Речь пойдет не о случайных действиях, а об алгоритмах, использующих случайность (вероятностных алгоритмах). Наряду с «обычными» действиями в вероятностном алгоритме разрешается «подбрасывание монетки», то есть использование случайных равномерно распределенных битов.

Результат работы вероятностного алгоритма точно не определен. Можно лишь говорить о вероятности того или иного результата. Алгоритм считается хорошим, если вероятность ошибки не слишком велика. Такое расплывчатое описание, конечно, нуждается в уточнении. С практической точки зрения интересны только те алгоритмы, которые ошибаются очень редко.

Во многих случаях сравнительно легко уменьшить вероятность ошибки вероятностного алгоритма. Для этого алгоритм запускается несколько раз и выбирается тот ответ, который встречается чаще всего. Вероятность ошибки будет довольно быстро убывать. Приведем пример. Если вероятность ошибки алгоритма равна 0,4 (многовато, не правда ли?), то при повторении его работы вероятность ошибки будет уменьшаться вдвое примерно за тридцать повторений. Выполнив алгоритм тысячу раз, мы достигнем вероятности ошибки 10-9; две тысячи повторений дадут 10-18, что более чем достаточно с практической точки зрения. Такая процедура называется усилителем вероятности.

Как появились вероятностные алгоритмы

Классическое представление об алгоритме: это точный рецепт получения результата, который можно реализовать, используя заранее оговоренный набор простейших действий.

Пока алгоритмы использовались в основаниях математики, ничего иного и не требовалось. Имея строгое определение алгоритма, математики получили возможность отвечать на вопрос: существует ли для данной задачи алгоритм ее решения? Почти во всех практически интересных случаях на этот вопрос удается ответить.

Появление компьютеров привело к постановке новых вопросов. Оказалось, что есть алгоритмические задачи, непосильные для компьютеров 1. Дело в том, что некоторые алгоритмы работают очень медленно. Возьмем хрестоматийный пример. Хорошо известно 2, что существует алгоритм решения любых задач элементарной геометрии. Подавая на вход такого алгоритма описание геометрической задачи, на выходе получим ее решение. Однако ждать придется долго. Точные оценки времени его работы зависят, конечно, от подробностей реализации, но не будет грубой ошибкой сказать, что универсальный алгоритм решения геометрических задач затратит на решение всех задач из школьного учебника время, заведомо превышающее время существования Вселенной 3.

Эффективными алгоритмами занимается теория сложности вычислений. В ней учитываются ограничения, накладываемые на вычисления в реальном мире. При этом все базируется на простейшей метафоре. Вычислительная машина, как и всякая машина, потребляет некоторый ресурс. А поскольку ресурсы окружающего мира ограничены 4, то алгоритмы, требующие их слишком много, реализовать невозможно. Основными вычислительными ресурсами, очевидно, являются время вычисления и требуемая для вычислений память 5.

Интересно, что если одновременно используется несколько вычислительных ресурсов, между ними возможен «обмен» (trade-off): скажем, увеличивая память, можно сократить время вычисления.

Случайные биты — и это замечательно! — тоже являются своеобразным вычислительным ресурсом. Вероятностные алгоритмы используют его, чтобы сократить потребление другого ресурса (обычно времени вычисления).

Каким же образом случайность экономит время? Рассмотрим самую общую ситуацию.

Случайный поиск

Допустим, нужно оценить, насколько часто встречается некоторое свойство. Общее количество возможных вариантов слишком велико для прямого перебора. Тогда можно поступить следующим образом: выбирая варианты случайно и равновероятно, подсчитать частоту выполнения свойства на полученной выборке.

Таким образом, выбор случайного варианта позволяет в некотором ослабленном смысле произвести большой перебор вариантов за небольшое время. Можно с некоторой натяжкой сказать, что вероятностный поиск «распараллеливает» перебор вариантов.

Отметим важное требование — использовать при таком поиске равномерное распределение на возможных вариантах. В алгоритмических задачах этому требованию не всегда легко удовлетворить. Легко выбрать случайную последовательность нулей и единиц (это ведь и есть последовательность результатов случайного подбрасывания монетки). Немного труднее выбрать случайное слово заданной длины в алфавите, число букв в котором не является степенью двойки. Еще чуть труднее построить случайную перестановку в соответствии с равномерным распределением. Но часто условия бывают гораздо сложнее, и построение равномерного распределения становится трудной математической задачей.

Проверка простоты числа

Самый известный и важный с практической точки зрения пример эффективного вероятностного алгоритма — проверка простоты числа. Напомним, что натуральное число называется простым, если оно делится нацело только на единицу и на само себя. Скажем, 3, 5, 7 — числа простые, а 9 — нет. Когда числа маленькие, проверку простоты легко выполнить, проверяя делимость на все числа, меньшие данного 6. Но что делать, если нужно проверить, скажем, число 170141183460469231731687?

Тем не менее, ответ можно получить буквально за несколько секунд на персональном компьютере (ввод этого числа с клавиатуры займет больше времени). Число — составное, хотя алгоритм и не говорит ничего о том, каковы его делители (используются косвенные признаки простоты числа).

Алгоритм проверки простоты устроен так, что ответ «число — не простое» он дает с достоверностью (вероятность ошибки 0). А вот если ответ «число — простое», то существует некоторая вероятность ошибки, которую можно сделать достаточно малой, используя описанное выше усиление вероятностей. (Алгоритмы такого типа называются Лас-Вегас-алгоритмами, в противоположность алгоритмам Монте-Карло, допускающими ошибки в обоих вариантах ответа. Такая терминология не подразумевает различия технологий в игорных домах Нового и Старого Света. Она возникла и прижилась случайно.)

Если перебирать числа одно за другим, начиная с приведенного выше, то первым «простым» окажется 29-е по счету число. Почему слово «простым» взято в кавычки? А потому, что утверждать наверняка простоту этого числа автор статьи не берется, поскольку проверка проводилась вероятностным алгоритмом. Можно лишь полагать, что вероятность ошибки мала.

Вероятностные алгоритмы долгое время смущали именно этим странным свойством. Приведенное выше число либо простое, либо нет. Как понимать утверждение, что оно простое с вероятностью ошибки меньше одной стомиллионной? Если бы на простоту этого числа опиралось доказательство какой-то теоремы, следовательно, теорема была бы верна лишь с некоторой вероятностью?!

Делалось множество попыток построить эффективный алгоритм проверки простоты числа. Наилучшее на сегодняшний день достижение выглядит довольно странно: если верна некоторая математическая гипотеза (вариант знаменитой гипотезы Римана о нулях дзета-функции), то эффективный алгоритм проверки простоты существует. Если же эта гипотеза неверна, то ничего пока сказать нельзя. Замечательно, не правда ли?

Совершенные паросочетания

Иногда применение вероятностных алгоритмов дает более скромный выигрыш в скорости, чем в случае проверки простоты числа. В качестве примера приведем задачу о совершенном паросочетании в графе. Сформулировать ее можно так. Пусть в путешествие отправилась группа людей. Известно, кто с кем дружит. Можно ли расселить людей по двухместным каютам так, чтобы в каждой каюте оказались друзья?

Для задачи о совершенном паросочетании есть эффективные детерминированные алгоритмы. Есть, однако, и очень простой вероятностный алгоритм, допускающий множество обобщений на более трудные случаи. Он эксплуатирует следующее наблюдение из алгебры: количество корней у ненулевого многочлена от одной переменной не превосходит его степени. Если переменных несколько, то утверждение становится чуть более сложным, но его суть сохраняется: корней у ненулевого многочлена по-прежнему мало. Поэтому значение ненулевого многочлена в наугад взятой точке будет отлично от нуля с большой вероятностью!

Вычислить значение этого многочлена можно быстро, а вот выписать все его коэффициенты — нет. (Для группы из двадцати человек количество коэффициентов в многочлене гораздо больше приведенного выше гигантского числа.) Выбрав случайно значения переменных этого многочлена в достаточно большом диапазоне, можно проверить, равно ли нулю значение многочлена. Если не равно, то совершенное паросочетание есть (хотя вычисление и не дает никакого намека на то, кого с кем сочетать). А если несколько случайных попыток дают 0, можно с большой вероятностью утверждать, что совершенного паросочетания нет.

Время работы такого вероятностного алгоритма незначительно отличается от времени работы более громоздких детерминированных алгоритмов. Впрочем, это справедливо лишь для компьютеров, где все вычисления проводятся последовательно. Если же решать задачу о совершенном паросочетании на компьютере, состоящем из большого количества параллельно работающих процессоров, то мы получаем ощутимый выигрыш во времени.

Экзотические модели вычислений

Компьютеры используются не только для решения задач, но и для общения. Сейчас уже правильнее говорить «не столько для решения задач, сколько для общения». При этом возникают проблемы совершенно иного рода, связанные с необходимостью защиты информации.

Для многих из этих проблем придуманы точные математические формулировки. Не вдаваясь в подробности математической криптографии, скажем лишь, что типичная ситуация, которую нужно исследовать, — это общение обычного алгоритма, ограниченного в ресурсах, с некоторым всезнающим существом. (В криптографии всезнающее существо моделирует возможного противника, желающего перехватить вашу информацию или обмануть вас тем или иным способом. Поскольку заранее противник не определен, принимается такая, несколько параноидальная точка зрения: противник может делать все, что не запрещено законами природы.)

В задачах, где предусматривается общение со всезнающим оппонентом, применение вероятностных алгоритмов дает удивительные результаты. Приведем три ярких примера.

Пример 1. Пристрастный советник.

Пусть алгоритм решает некоторую задачу, в которой ответом является «да» или «нет», и имеет возможность консультироваться со всезнающим советником. У советника есть только один недостаток: он преследует свои собственные цели и поэтому необязательно говорит правду. Цель советника в том, чтобы было принято положительное решение. Тогда алгоритм должен быть устроен так, чтобы в случае, когда ответ отрицательный, ответы советника не могли привести к принятию положительного решения.

Оказывается, существуют вероятностные алгоритмы использования такого пристрастного советника, позволяющие со сколь угодно малой вероятностью ошибки решать все задачи, которые можно решить, используя не слишком большую память (без ограничений на время вычисления). Типичным примером подобной задачи является поиск выигрышной стратегии для позиционной игры. Глядя на ситуацию со стороны советника, можно сказать и так: игра против любого противника, использующего сколь угодно сложную стратегию, оказывается не сложнее игры с природой (природа — это противник, стратегия действий которого считается известной, но допускает случайный выбор).

Математика, лежащая в основе этих алгоритмов, не так уж сложна, но непривычна. Например, приходится расширять область логических значений, заменяя 0 и 1 (ложь и истину) на набор остатков по модулю достаточно большого простого числа. Смысл такого действия и сегодня остается непонятым.

Пример 2. PCP-теорема.

Это теорема, доказанная в начале 1990-х годов, произвела настолько сильное впечатление, что о ней писала даже нематематическая пресса (например, газета «New York Times»). В вольном пересказе она формулируется следующим образом: можно придумать такой способ записи математических доказательств, при котором проверять (в вероятностном смысле, то есть с небольшой вероятностью ошибки) правильность доказательства можно, изучив несколько случайно выбранных мест в доказательстве (их число не зависит от длины доказательства!).

Другая, более практическая интерпретация звучит так. Вы решаете некоторую сложную задачу, используя суперкомпьютер. Однако вы не доверяете надежности его работы и хотите проверить правильность вычислений на домашнем компьютере. Очевидно, что полная проверка займет слишком много времени. Вместо этого вы просите суперкомпьютер произвести вычисления в определенном формате и переслать вам некоторое количество выбранных вами контрольных точек.

Сила PCP-теоремы в том, что объем запрашиваемой у суперкомпьютера информации не зависит от объема проделанных им вычислений, а определяется лишь той вероятностью ошибки, которую вы согласны допустить.

Пример 3. Доказательства с нулевым разглашением.

Рассмотрим такую ситуацию. Вы обращаетесь к эксперту с тем, чтобы он решил некоторую интересующую вас задачу, которую не можете решить самостоятельно. При этом вы не доверяете эксперту (вдруг он, как и вы, не умеет решать задачу 7?). А эксперт, в свою очередь, не доверяет вам. Поэтому вы не хотите платить деньги эксперту, пока он не убедит вас в том, что он умеет решать задачу, а эксперт не хочет давать вам никакой информации о решении, пока вы не заплатите ему за работу.

Выход из тупика есть. Можно организовать общение между заказчиком и экспертом так, чтобы первый убедился в квалификации второго, но не получил при этом ни бита информации о решении.

Разумеется, точная формулировка этого утверждения более сложная, причем доказательство корректности предлагаемого протокола основано, как почти всегда бывает, на недоказанных гипотезах о трудности решения некоторых конкретных задач. В данном случае речь идет о задаче проверки изоморфизма графов 8.

Дополнительные возможности: квантовые вероятности

Квантовые компьютеры активно обсуждаются в последние годы, несмотря на то (а быть может, даже благодаря тому), что они пока не существуют «в железе». Интерес к квантовым вычислениям скачкообразно вырос после того, как П. Шор придумал эффективный квантовый алгоритм факторизации числа (разложения на простые множители). Это задача гораздо труднее задачи проверки простоты числа. Например, требуются многие часы (если не недели) вычислений, чтобы найти простые делители числа, приведенного выше.

Квантовые алгоритмы напоминают вероятностные. Прежде всего, неопределенностью результата. Когда считывается (физики предпочитают говорить: измеряется) результат работы квантового вычислителя, могут получаться разные значения, вероятности которых определяются законами квантовой механики.

Если использовать в вычислительном устройстве разрозненные квантовые биты, то получающаяся неопределенность ничем не отличается от обычной случайности. Именно такие системы могут служить идеальными датчиками случайных чисел. Реализовать их нетрудно. К примеру, долгоживущий радиоактивный изотоп можно использовать как практически неисчерпаемый источник случайных битов 9.

Особые свойства квантовых вычислителей проявляются лишь тогда, когда по правилам квантовой механики функционирует система взаимодействующих квантовых битов. Возникают явления интерференции, благодаря которым вероятности могут не только складываться, но и вычитаться. В самом грубом приближении это и придает квантовым компьютерам дополнительные вычислительные возможности.

Попробуем (крайне грубо) описать один из простейших квантовых алгоритмов — алгоритм Гровера. Он решает универсальную задачу перебора, состоящую в том, что нужно найти ответ на некоторый вопрос, используя «оракул», или «черный ящик» — устройство, которое на предложенный ему вариант ответа сообщает, подходит этот вариант или нет.

Действуя классическим способом, в такой ситуации можно лишь перебирать один за другим возможные варианты ответа. Если использовать случайный выбор, можно сократить перебор примерно вдвое. А применение квантового алгоритма позволяет сократить перебор гораздо сильнее: нужное количество запросов будет пропорционально квадратному корню из числа возможных вариантов. Если вариантов 1000 — квантовому алгоритму потребуется 100 попыток, если вариантов 100 миллионов, то 10000 попыток.

Обратите внимание, что такое сокращение времени работы специалисты по теории сложности считают непринципиальным. Их устраивает только экспоненциальное ускорение перебора. Причина в том, что в практически важных случаях вариантов перебора гораздо больше. Допустим, ответ записывается 64 байтами. Число, о котором шла речь в разделе про проверку простоты, намного меньше, чем количество возможных состояний 64 байт (а значит, вариантов ответа). Корень из этого числа «намного меньше», но все же значительно превосходит количество всех сложений, сделанных на планете Земля в двадцатом веке (как людьми, так и компьютерами).

Как же устроено ускорение перебора в алгоритме Гровера? Для этого сооружается еще один оракул, на этот раз полностью нами контролируемый 10. Этот вспомогательный оракул считает правильным ответом «равномерную смесь» всех возможных вариантов ответа. То, что мы назвали «равномерной смесью», является особым квантовым состоянием, которое при измерениях действительно будет давать все возможные варианты равновероятно. Но если теперь мы составим сложную систему из исходного и построенного нами оракула и начнем задавать им вопросы попеременно, начиная с правильного ответа на наш вспомогательный вопрос, то спустя некоторое количество вопросов (как уже говорилось, пропорциональное квадратному корню из числа вариантов) измерение зафиксирует со значительной вероятностью правильный ответ на вопрос исходного оракула.

Пояснить это довольно трудно. Разве что можно вспомнить эпизод из известного мультфильма, где почтальон общается через дверь с говорящей птицей, которая повторяет одно и то же: «Кто там?» Почтальон отвечает: «Это я, почтальон Печкин…» И так много-много раз. Заканчивается все тем, что почтальон вопрошает: «Кто там?» и получает в ответ: «Это я, почтальон Печкин».

Вот так и квантовые оракулы: если задавать им вопросы очень долго, то правильный ответ одного превращается в правильный ответ другого… «Почему?» — спросите вы. «Потому, что композиция двух отражений в плоскости есть поворот», — загадочно ответит автор. Тем читателям, кто понимает, о чем идет речь в ответе, рекомендую почитать более точные описания алгоритма Гровера и вообще познакомиться с квантовой механикой. Остальным лучше начать с линейной алгебры.

Насколько велики возможности квантовых алгоритмов? Как вы уже догадываетесь, точного ответа на этот вопрос нет. Зато наблюдается удивительная аналогия со случаем вероятностных алгоритмов. Есть небольшое количество примеров, когда достигается принципиальный выигрыш по сравнению с классическими детерминированными алгоритмами: проверка простоты для вероятностных вычислений, факторизация — для квантовых. Есть примеры, когда выигрыш не столь принципиален, но имеются другие преимущества. Для вероятностных алгоритмов это, например, задача о совершенном паросочетании. Для квантовых — универсальная задача перебора. Для более сложных моделей и вероятностные, и квантовые вычисления дают значительные усиления. Скажем, описанный выше вероятностный диалог с советником может быть квантовым образом упакован всего в два раунда.

В чем смысл этой аналогии, неясно. Вполне возможно, это просто случайное совпадение. А быть может, отражение некоторой закономерности, настолько общей, что ею должны интересоваться философы, а не математики.

1 (обратно к тексту) — Имеется в виду любое вычислительное устройство, реализация которого хотя бы в принципе возможна в физическом мире.
2 (обратно к тексту) — Первым это доказал А. Тарский — один из создателей теории алгоритмов.
3 (обратно к тексту) — Оговорка про универсальность важна: существуют программы, которые во многих случаях за приемлемое время доказывают геометрические теоремы, хотя и не всегда добиваются успеха. Программа такого типа может справиться с задачником по геометрии гораздо быстрее.
4 (обратно к тексту) — Некоторые физики утверждают, что в нашем распоряжении есть всего-навсего 1080 элементарных частиц.
5 (обратно к тексту) — По большому счету, это пространство и время.
6 (обратно к тексту) — На самом деле, достаточно проверить только числа, не превосходящие квадратный корень из данного числа.
7 (обратно к тексту) -Ситуация вполне «из жизни». Не правда ли? — Ю.Р.
8 (обратно к тексту) — Ее формулировка звучит так: можно ли перенумеровать вершины двух графов таким образом, чтобы в обоих графах вершины с одинаковыми номерами были либо соединены ребром, либо нет.
9 (обратно к тексту) — Мы опускаем сейчас тонкости, связанные с тем, что закон распределения получающихся битов отличается от равномерного. Скажем лишь, что он нам заранее известен.
10 (обратно к тексту) — В том смысле, что его поведение нам всегда известно. Полностью контролируемый оракул — согласитесь, это так знакомо! — Ю.Р.

Источник

12.2. Испытание простоты чисел

Если формулы получения простых чисел, подобно формулам Ферма или Мерсенна, не гарантируют, что полученные числа — простые, то как мы можем генерировать большие простые числа для криптографии? Мы можем только выбрать случайно большое число и провести испытание, чтобы убедиться, что оно — простое.

Нахождение алгоритма, который правильно и эффективно проверяет очень большое целое число и устанавливает: данное число – простое это число или же составной объект, — всегда было проблемой в теории чисел и, следовательно, в криптографии. Однако, недавние исследования (одно из которых мы обсуждаем в этом разделе) выглядят очень перспективными.

Алгоритмы, которые решают эту проблему, могут быть разделены на две обширные категории — детерминированные алгоритмы и вероятностные алгоритмы. Ниже рассматриваются некоторые представители обеих категорий. Детерминированный алгоритм всегда дает правильный ответ. Вероятностный алгоритм дает правильный ответ в большинстве, но не во всех случаях. Хотя детерминированный алгоритм идеален, он обычно менее эффективен, чем соответствующий вероятностный.

Детерминированные алгоритмы

Детерминированный алгоритм, проверяющий простоту чисел, принимает целое число и выдает на выходе признак: это число — простое число или составной объект. До недавнего времени все детерминированные алгоритмы были неэффективны для нахождения больших простых чисел. Как мы коротко покажем, новые взгляды делают эти алгоритмы более перспективными.

Алгоритм теории делимости

Самое элементарное детерминированное испытание на простоту чисел — испытание на делимость. Мы используем в качестве делителей все числа, меньшие, чем 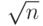sqrt n . Если любое из этих чисел делит n, тогда n — составное. Алгоритм 12.1 показывает проверку на делимость в ее примитивной и очень неэффективной форме.

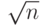
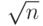
Алгоритм может быть улучшен, если проверять только нечетные номера. Он может быть улучшен далее, если использовать таблицу простых чисел между 2 и sqrt n . Число арифметических операций в алгоритме 12.1 — sqrt n . Если мы принимаем, что каждая арифметическая операция использует только операцию на один бит (чисто условное соглашение), тогда сложность разрядной операции алгоритма 12.1 — sqrt {{2^{{n_b}}}} = {2^{{raise0.7exhbox{${{n_b}}$} !mathord{left/ {vphantom {{{n_b}} 2}}right.kern-nulldelimiterspace} !lower0.7exhbox{$2$}}}} , где nb – число битов в n. В больших системах, обозначаемых О, сложность может быть оценена O(2n): экспоненциально (см. приложение L). Другими словами, алгоритм делимости неэффективен, если nb большое.

Сложность побитного испытания делимостью показательна.

Пример 12.18

Предположим, что n имеет 200 битов. Какое число разрядных операций должен был выполнить алгоритм делимости?

Решение

Сложность побитовых операций этого алгоритма — {2^{{raise0.7exhbox{${{n_b}}$} !mathord{left/ {vphantom {{{n_b}} 2}}right.kern-nulldelimiterspace} !lower0.7exhbox{$2$}}}} . Это означает, что алгоритму необходимо провести 2100 битовых операций. Если алгоритм имеет скорость 230 операций в секунду, то необходимо 270 секунд для проведения испытаний. 

ttparindent0pt

Тест на делимость (n)

         //n – число тестов на простоту

{ 

  r gets  2

  while (r < sqrt n)

    { 

    if (r|n) return "a composite"  // составное

    r gets  r+1

   } 

  return "a prime"  //простое

}

12.1.

AKS-алгоритм

В 2002 г. индийские ученые Агравал, Каял и Сахсена (Agrawal, Kayal и Saxena) объявили, что они нашли алгоритм для испытания простоты чисел с полиномиальной сложностью времени разрядных операций 0 ((log2nb)). Алгоритм использует тот факт, что 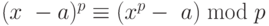{(x{text{ }}-a)^p} equiv ({x^p}-{text{ }}a)bmod p. Интересно наблюдать, что некоторые будущие разработки делают этот алгоритм стандартным тестом для определения простоты чисел в математике и информатике.

Пример 12.19

Предположим, что n имеет 200 битов. Какое число разрядных операций должен был выполнить алгоритм AKS?

Решение

Сложность разрядной операции этого алгоритма — O((log 2 n b) 12). Это означает, что алгоритму надо только (log2 200) 12 = 39 547 615 483 битовых операций. На компьютере, способном выполнить 1 миллиард битов в секунду, алгоритму требуется только 40 секунд.

Вероятностные алгоритмы

До AKS-алгоритма все эффективные методы для испытания простоты чисел были вероятностные. Эти методы могут использоваться еще некоторое время, пока AKS формально не принят как стандарт.

Вероятностный алгоритм не гарантирует правильность результата. Однако мы можем получить вероятность ошибки настолько маленькую, что это почти гарантирует, что алгоритм вырабатывает правильный ответ. Сложность разрядной операции алгоритма может стать полиномиальной, при этом мы допускаем небольшой шанс для ошибок. Вероятностный алгоритм в этой категории возвращает результат либо простое число, либо составной объект, основываясь на следующих правилах:

a. Если целое число, которое будет проверено, — фактически простое число, алгоритм явно возвратит простое число.

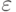
b. Если целое число, которое будет проверено, — фактически составной объект, алгоритм возвращает составной объект с вероятностью 1 - varepsilon , но может возвратить простое число с varepsilon вероятности. Вероятность ошибки может быть улучшена, если мы выполняем алгоритм несколько раз с различными параметрами или с использованием различных методов. Если мы выполняем алгоритм m раз, вероятность ошибки может уменьшиться до m.

Тест Ферма

Первый вероятностный метод, который мы обсуждаем, — испытание простоты чисел тестом Ферма.

Если n — простое число, то 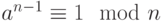a^{n-1}equiv 1 mod n.

Обратите внимание, что если n — простое число, то сравнение справедливо. Это не означает, что если сравнение справедливо, то n — простое число. Целое число может быть простым числом или составным объектом. Мы можем определить следующие положения как тест Ферма:

ttparindent0pt Если n — простое число, то a^{n-1} equiv 1 mod n Если n — составной объект, то возможно, что a^{n-1} equiv 1 mod n

Простое число удовлетворяет тесту Ферма. Составной объект может пройти тест Ферма с вероятностью 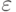varepsilon . Сложность разрядной операции испытания Ферма равна сложности алгоритма, который вычисляет возведение в степень. Позже в этой лекции мы приводим алгоритм для быстрого возведения в степень со сложностью разрядной операции O(nb ), где О — номер битов в n. Вероятность может быть улучшена, если проверка делается с несколькими числами (a1, a2 и так далее). Каждое испытание увеличивает вероятность, что испытуемое число – это простое число.

Пример 12.20

Проведите испытание Ферма для числа 561.

Решение

Используем в качестве основания число 2.

2561-1 = 1 mod 561

Число прошло тест Ферма, но это — не простое число, потому что

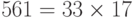
561 = 33 times 17.

Испытание квадратным корнем

В модульной арифметике, если n — простое число, то квадратный корень равен только 1 (либо +1, либо –1). Если n — составной объект, то квадратный корень — +1 или (-1), но могут быть и другие корни. Это называют испытанием простоты чисел квадратным корнем. Обратите внимание, что в модульной арифметике –1 означает n–1.

ttparindent0pt Если n — простое число, $sqrt 1 mod n = pm 1$ Если n — составной объект, $sqrt 1 mod n = pm 1$, и возможны другие значения

Пример 12.21

Каковы квадратные корни 1 mod n, если n равно 7 (простое число)?

Решение

Единственные квадратные корни 1 mod n – это числа 1 и –1. Мы можем видеть, что

12 = 1 mod 7	  (–1)2 = 1 mod 7
22 = 4 mod 7	  (–2)2 = 4 mod 7
32 = 2 mod 7	  (–3)2 = 2 mod 7

Заметим, что тест не дает результатов для 4, 5 и 6, потому что 4 = –3 mod 7,
5 = –2 mod 7 и 6 = –1 mod 7.

Пример 12.22

Каков квадратный корень из 1 mod n, если n равно 8 (составное)?

Решение

Имеется три решения: 1, 3, 5 и 7 (которые дают –1). Мы можем также видеть, что

12 = 1 mod 8	  (–1)2 = 1 mod 8
32 = 1 mod 8	  (–5)2 = 1 mod 8

Пример 12.23

Каков квадратный корень из 1 mod n, если n равно 17 (простое)?

Решение

Имеются только два решения, соответствующие поставленной задаче: это 1 и (–1). 

12 = 1 mod 17	  (-1)2 = 1 mod 17
22 = 4 mod 17	  (-2)2 = 4 mod 17
32 = 9 mod 17	  (-3)2 = 9 mod 17
42 = 16 mod 17	  (-4)2 = 16 mod 17
52 = 8 mod 17	  (-5)2 = 8 mod 17
62 = 2 mod 17	  (-6)2 = 2 mod 17
72 = 15 mod 17	  (-7)2 = 15 mod 17
82 = 13 mod 17	  (-8)2 = 13 mod 17

Заметим, что не надо проверять целые числа, большие 8, потому что 9 = –8 mod 17

Пример 12.24

Каков квадратный корень из 1 mod n, если n равно 22 (составное)?

Решение

Сюрприз в том, что имеется только два решения: +1 и –1, хотя 22 — составное число. 

12    = 1 mod 22
(-1)2 = 1 mod 22

Хотя во многих случаях имеется испытание, которое показывает нам однозначно, что число составное, но это испытание провести трудно. Когда дано число n, то все числа, меньшие, чем n (кроме чисел 1 и n–1), должны быть возведены в квадрат, чтобы гарантировать, что ни одно из них не равно 1. Это испытание может использоваться для чисел (не +1 или –1), которые в квадрате по модулю n дают значение 1. Этот факт помогает в испытании Миллера–Рабина, которое рассматривается в следующем разделе.

Источник

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

  • 1 О природе переобучения
  • 2 Определения
    • 2.1 Вероятность переобучения (частотное определение)
    • 2.2 Вероятность переобучения (вероятностное определение)
  • 3 Теоретические верхние оценки переобученности
    • 3.1 Сложность
    • 3.2 Разделимость
    • 3.3 Устойчивость
  • 4 Эмпирическое измерение переобучения
  • 5 См. также
  • 6 Ссылки
  • 7 Литература

Обобщающая способность (generalization ability, generalization performance).
Говорят, что алгоритм обучения обладает способностью к обобщению, если вероятность ошибки на тестовой выборке достаточно мала или хотя бы предсказуема, то есть не сильно отличается от ошибки на обучающей выборке.
Обобщающая способность тесно связана с понятиями переобучения и недообучения.

Переобучение, переподгонка (overtraining, overfitting) — нежелательное явление, возникающее при решении задач обучения по прецедентам, когда вероятность ошибки обученного алгоритма на объектах тестовой выборки оказывается существенно выше, чем средняя ошибка на обучающей выборке.
Переобучение возникает при использовании избыточно сложных моделей.

Недообучение — нежелательное явление, возникающее при решении задач обучения по прецедентам, когда алгоритм обучения не обеспечивает достаточно малой величины средней ошибки на обучающей выборке.
Недообучение возникает при использовании недостаточно сложных моделей.

Пример.
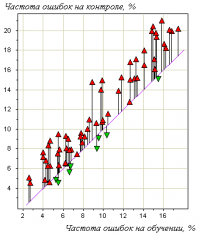
На рисунке справа показан эффект переобучения в одной задаче медицинского прогнозирования.
Точки на графике соотвествуют различным методам обучения.
Каждая точка получена путём усреднения по большому числу разбиений исходной выборки из 72 прецедентов на обучающую подвыборку и контрольную.
Горизонтальная ось — частота ошибок на обучении; вертикальная — на контроле.
Хорошо видно, что точки имеют систематическое смещение вверх относительно диагонали графика.

О природе переобучения

Переобучение в задаче прогнозирования долгосрочного результата хирургического лечения атеросклероза.

Переобучение в задаче прогнозирования долгосрочного результата хирургического лечения атеросклероза.

Эмпирическим риском называется средняя ошибка алгоритма на обучающей выборке.
Метод минимизации эмпирического риска (empirical risk minimization, ERM) наиболее часто применяется для построения алгоритмов обучения.
Он состоит в том, чтобы в рамках заданной модели выбрать алгоритм, имеющий минимальное значение средней ошибки на заданной обучающей выборке.

С переобучением метода ERM связано два утверждения, которые на первый взгляд могут показаться парадоксальными.

Утверждение 1.
Минимизация эмпирического риска не гарантирует, что вероятность ошибки на тестовых данных будет мала.
Легко строится контрпример — абсурдный алгоритм обучения, который минимизирует эмпирический риск до нуля, но при этом абсолютно не способен обучаться.
Алгоритм состоит в следующем.
Получив обучающую выборку, он запоминает её и строит функцию, которая сравнивает предъявляемый объект с запомненными обучающими объектами.
Если предъявляемый объект в точности совпадает с одним из обучающих, то эта функция выдаёт для него запомненный правильный ответ.
Иначе выдаётся произвольный ответ (например, случайный или всегда один и тот же).
Эмпирический риск алгоритма равен нулю, однако он не восстанавливает зависимость и не обладает никакой способностью к обобщению.

Вывод: для успешного обучения необходимо не только запоминать, но и обобщать.

Утверждение 2.
Переобучение появляется именно вследствие минимизации эмпирического риска.
Пусть задано конечное множество из D алгоритмов, которые допускают ошибки независимо и с одинаковой вероятностью.
Число ошибок любого из этих алгоритмов на заданной обучающей выборке подчиняется одному и тому же биномиальному распределению.
Минимум эмпирического риска — это случайная величина, равная минимуму из D независимых одинаково распределённых биномиальных случайных величин.
Её ожидаемое значение уменьшается с ростом D.
Соотвественно, с ростом D увеличивается переобученность — разность вероятности ошибки и частоты ошибок на обучении.

В данном модельном примере легко построить доверительный интервал переобученности, так как функция распределения минимума известна.
Однако в реальной ситуации алгоритмы имеют различные вероятности ошибок, не являются независимыми,
а множество алгоритмов, из которого выбирается лучший, может быть бесконечным.
По этим причинам вывод количественных оценок переобученности является сложной задачей, которой занимается теория вычислительного обучения.
До сих пор остаётся открытой проблема сильной завышенности верхних оценок вероятности переобучения.

Утверждение 3.
Переобучение связано с избыточной сложностью используемой модели. Всегда существует оптимальное значение сложности модели, при котором переобучение минимально.

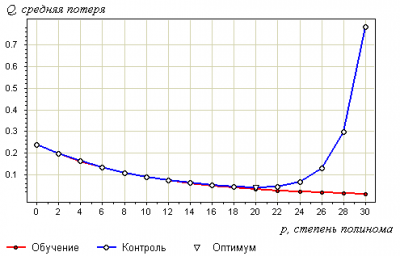
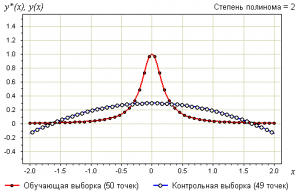
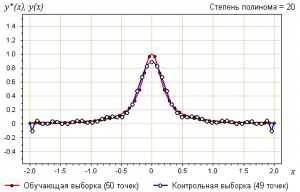
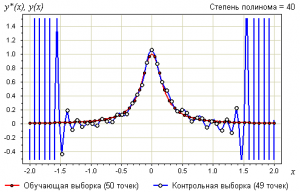
График зависимости средней потери на обучении и на контроле от степени полинома.

График зависимости средней потери на обучении Q(a,X^m) и на контроле Q(a,X^k) от степени полинома.

Пример.
Рассмотрим задачу аппроксимации вещественной функции y(x) = frac1{1+25x^2} по обучающей выборке из 50 точек X^m = left{ x_i = 4frac{i-1}{m-1}-2 right}. Это равномерная сетка на отрезке [-2,2].

В качестве модели рассмотрим полиномы заданной степени p:

a(x,w) = w_0 + w_1 x + cdots + w_p x^p.

В качестве метода обучения возьмём метод наименьших квадратов:

sum_{i=1}^m bigl( y(x_i) - a(x_i,w) bigr)^2 to min_w.

Таким образом, функция потерь квадратична:
mathcal{L}(a,x) = bigl( y(x) - a(x) bigr)^2.

Возьмём контрольную выборку — также равномерную сетку на отрезке [-2,2], узлы которой находятся в точности между узлами первой сетки: X^k = Bigl{ x'_i = 4frac{i-0.5}{m-1}-2 Bigr}.

Зададимся вопросом:
что будет на контрольной выборке при увеличении степени полинома p?
Степень связана с числом свободных параметров модели, то есть играет роль сложности модели.

Ниже показаны графики самой выборки и аппроксимирующей функции:



Определения

Основные обозначения:

X^m={x_1,ldots,x_m} — подмножество (выборка) объектов из множества объктов mathbb{X},
A — множество алгоритмов,
mathcal{L}:: Atimes mathbb{X} to mathbb{R} — функция потерь, значение mathcal{L}(a,x) есть величина потерь, возникающих при применении алгоритма a к объекту x.

Средней потерей алгоритма a на выборке X^m называется величина

Q(a,X^m) = frac1m sum_{i=1}^m mathcal{L}(a,x_i).

Пусть mathbb{X} — вероятностное пространство.
Ожидаемой потерей алгоритма a называется величина

P(a) = mathbb{E}mathcal{L}(a,x).

Если функция mathcal{L} бинарная (возвращяет либо 0, либо 1), то Q(a,X^m) называется частотой ошибок, а P(a) — вероятностью ошибки алгоритма a.

Не столь важно, что скрывается за термином «алгоритм».
Это могут быть в частности, решающие правила в задачах классификации и распознавания образов, функции регрессии в задачах восстановления регрессии илипрогнозирования, и т. п.

Определение.
Методом обучения (или алгоритмом обучения) называется отображение mu:: mathbb{X}^m to A, которое произвольной обучающей выборке X^m ставит в соответствие некоторый алгоритм a = mu(X^m).

Вероятность переобучения (частотное определение)

Определение.
Переобученностью алгоритма a = mu(X^m) относительно контрольной выборки X^k называется разность

delta(a,X^m,X^k) = Q(a,X^k)-Q(a,X^m).

Определение.
Вероятностью переобучения называется вероятность того, что величина переобученности превысит заданный порог varepsilon:

Q_eps(mu,X^{m+k}) = mathbb{P} bigl[ delta(a,X^m,X^k) geq varepsilon bigr],

где вероятность mathbb{P} можно понимать в смысле равномерного распределения на множестве всех C_{m+k}^m разбиений выборки X^L = X^m sqcup X^k на наблюдаемую обучающую X^m и скрытую контрольную X^k.

Вероятность переобучения может быть измерена эмпирически методом Монте-Карло,
см. также скользящий контроль:

hat Q_eps(mu,X^{m+k}) = frac1Nsum_{n=1}^N bigl[ delta(a,X_n^m,X_n^k) geq varepsilon bigr],

где X^L = X_n^m sqcup X_n^k — N случайных разбиений заданной выборки X^L на обучающую подвыборку X_n^m и контрольную подвыборку X_n^k,; n=1,ldots,N.

Вероятность переобучения (вероятностное определение)

Определение.
Переобученностью алгоритма a = mu(X^m) называется разность

delta(a,X^m) = P(a)-Q(a,X^m).

Определение.
Вероятностью переобучения называется вероятность того, что величина переобученности превысит заданный порог varepsilon:

P_eps(mu,X^m) = mathbb{P} bigl[ delta(a,X^m) geq varepsilon bigr],

где mathbb{P} — вероятность в пространстве случайных незавичимых выборок X^m, взятых из одного и того же неизвестного распределения.

Недостатки вероятностного определения:

Теоретические верхние оценки переобученности

Сложность

Оценки Вапника-Червоненкиса, размерность Вапника-Червоненкиса

Критерий Акаике

Оценки, основанные на самоограничении (self-bounding)

Оценки, основанные на последовательности выборов (microchoice bounds)

Оценки, основанные на расслоении семейства алгоритмов (shell bounds)

Разделимость

Оценки, основанные на отступах (margin-based bounds)

Устойчивость

Устойчивость алгоритма обучения (algorithmic stability)

Эмпирическое измерение переобучения

Скользящий контроль

См. также

  • Расслоение и сходство алгоритмов (виртуальный семинар)
  • Слабая вероятностная аксиоматика
  • Полигон алгоритмов
  • Радемахеровская сложность

Ссылки

Overfitting — статья о переобучении в англоязычной Википедии.

Литература

  1. Hastie, T., Tibshirani, R., Friedman, J. The Elements of Statistical Learning, 2nd edition. — Springer, 2009. — 533 p.  (подробнее)
  2. Vapnik V.N. Statistical learning theory. — N.Y.: John Wiley & Sons, Inc., 1998. [1]
  3. Воронцов, К. В. Комбинаторная теория надёжности обучения по прецедентам: Дис. док. физ.-мат. наук: 05-13-17. — Вычислительный центр РАН, 2010. — 271 с.  (подробнее)
Источник

Глава 4

Вероятностные алгоритмы и их анализ

4.1Вероятностная проверка тождеств

Один из первых примеров вероятностных алгоритмов, более эффективных, чем детерминированные, был предложен Фрейвалдом для задачи проверки матричного равенства AB = C (см. [Fre77]).

Обычный детерминированный алгоритм заключается в перемножении матриц A и B и сравнении результата с C. Сложность такого алгоритма есть O(n3) при использовании стандартного алгоритма умножения матриц размера n n и O(n2:376) при использовании лучшего из известных быстрых алгоритмов матричного умножения [CW90].

Вероятностный алгоритм Фрейвалда для этой задачи имеет сложность O(n2) и заключается в умножении левой и правой частей на случайный булев вектор x = (x1; : : : ; xn) с последующим сравнением полученных векторов. Алгоритм выдает ответ, что AB = C, если ABx = Cx, и является алгоритмом с од-

157

158

Глава 4. ВЕРОЯТНОСТНЫЕ АЛГОРИТМЫ И ИХ АНАЛИЗ

носторонней ошибкой, т. е. ошибается только для случаев неравенства — легко видеть, что если алгоритм сообщает, что тождество не выполнено, то всегда AB ≠ C.

При этом ABx вычисляется как A(Bx), что и обеспечивает оценку сложности алгоритма O(n2). Следующая теорема обеспечивает корректность алгоритма.

Теорема 13. Пусть A, B, и C — n n матрицы, элементы которых принадлежат некоторому полю F, причем AB ≠ C. Тогда для вектора x, выбранного случайно и равномерно из f0; 1gn,

P fABx = Cxg 1/2:

Доказательство. Пусть D = AB C. Мы знаем, что D — не полностью нулевая матрица и хотим оценить вероятность того, что Dx = 0. Без ограничения общности можно считать, что ненулевые элементы имеются в первой строке и они располагаются перед нулевыми. Пусть d — вектор, равный первой строке матрицы D, и предположим, что первые k элементов в d — ненулевые. Имеем

PfDx = 0g PfdT x = 0g:

Но dT x = 0 тогда и только тогда, когда

Для каждого выбора x2; : : : ; xk правая часть этого равенства фиксирована и равна некоторому элементу v поля F. Вероятность того, что x1 равно v, не превосходит 12 , поскольку x1 равномерно распределено на двухэлементном множестве f0; 1g, а вероятность события dT x = 0 либо равна 12 , если правая часть принадлежит множеству f0; 1g, либо равна нулю в противном случае.

4.1. ВЕРОЯТНОСТНАЯ ПРОВЕРКА ТОЖДЕСТВ

159

Классическим примером задачи, где вероятностные алгоритмы традиционно успешно применяются, является задача проверки тождеств для многочлена от многих переменных.

Задача 17. Проверить для заданного полинома P (x1; : : : ; xn) выполнение тождества P (x1; : : : ; xn)

0:

Следующая лемма (см. [MR95]), по сути, описывает вероятностный алгоритм Монте–Карло с односторонней ошибкой.

Лемма 14. Пусть Q(x1; : : : ; xn) — многочлен от многих переменных степени d над полем F и пусть

SF — произвольное подмножество. Если r1; : : : ; rn выбраны случайно, независимо и равномерно из

S, то

d P (Q(r1; : : : ; rn) = 0 j Q(x1; : : : ; xn) ̸0) jSj:

Доказательство. По индукции по n.

Базисный случай n = 1 включает полиномы от одной переменной Q(x1) степени d. Поскольку каждый такой полином имеет не более d корней, вероятность того, что Q(r1) = 0 не превосходит jdSj .

Пусть теперь предположение индукции верно для всех полиномов, зависящих от не более n 1 переменной.

Рассмотрим полином Q(x1; : : : ; xn) и разложим его по переменной x1:

∑k

Q(x1; : : : ; xn) = xi1Qi(x2; : : : ; xn);

i=0

где k d — наибольшая степень x1 в Q.

160

Глава 4. ВЕРОЯТНОСТНЫЕ АЛГОРИТМЫ И ИХ АНАЛИЗ

Предполагая, что Q зависит от x1, имеем k > 0, и коэффициент при xk1, Qk(x2; : : : ; xn) не равен тождественно нулю. Рассмотрим две возможности.

Первая — Qk(r2; : : : ; rn) = 0. Заметим, что степень Qk не превосходит d k, и по предположению индукции вероятность этого события не превосходит (djSjk) .

Вторая — Qk(r2; : : : ; rn) ≠ 0. Рассмотрим следующий полином от одной переменной:

∑k

q(x1) = Q(x1; r2; r3; : : : ; rn) = Qi(r2; : : : ; rn)xi1:

i=0

Полином q(x1) имеет степень k и не равен тождественно нулю, т.к. коэффициент при xk1 есть Qk(r2; : : : ; rn). Базовый случай индукции дает, что вероятность события

q(r1) = Q(r1; r2; : : : ; rn) = 0

не превосходит jkSj .

Мы доказали два неравенства:

d k PfQk(r2; : : : ; rn) = 0g jSj ;

k PfQ(r1; r2; : : : ; rn) = 0j Qk(r2; : : : ; rn) ≠ 0g jSj:

Используя результат упражнения 4.1.1, мы получаем, что вероятность события Q(r1; r2; : : : ; rn) = 0 не превосходит суммы двух вероятностей (d k)/jSj и k/jSj, что дает в сумме желаемое d/jSj.

4.1. ВЕРОЯТНОСТНАЯ ПРОВЕРКА ТОЖДЕСТВ

161

Упражнение 4.1.1. Покажите, что для любых двух событий E1, E2,

PfE1g PfE1j E2g + PfE2g:

Упражнение 4.1.2. Имеется n n матрица A, элементами которой являются линейные функции fij(x) = aijx + bij.

Придумайте алгоритм Монте-Карло с односторонней ошибкой для проверки этой матрицы на вырожденность (det A 0).

Одной из многочисленных областей, где широко применяются вероятностные алгоритмы, являются параллельные и распределенные вычисления. Эффективным параллельным алгоритмом (или NCалгоритмом) называется алгоритм, который на многопроцессорной RAM (так называемой PRAM) с числом процессоров, не превосходящим некоторого полинома от длины входа, завершает работу за время, ограниченное полиномом от логарифма длины входа.

Построение эффективного детерминированного параллельного алгоритма (NC-алгоритма) для нахождения максимального паросочетания в двудольном графе является одной из основных открытых проблем в теории параллельных алгоритмов. Удалось, однако, построить эффективный параллельный вероятностный алгоритм нахождения максимального паросочетания в двудольном графе (так называемый RNC-алгоритм) [MR95]. Примеры применения вероятностных алгоритмов для построения эффективных параллельных и распределенных алгоритмов рассматриваются в разделе 4.3.

162

Глава 4. ВЕРОЯТНОСТНЫЕ АЛГОРИТМЫ И ИХ АНАЛИЗ

4.2Вероятностные методы

вперечислительных задачах

Вданном разделе мы рассмотрим перечислительные задачи и изучим, как вероятностные методы могут быть применены для решения таких задач.

Алгоритм для решения перечислительной задачи получает на вход конкретные входные данные рассматриваемой задачи (например, граф) и в качестве выхода выдает неотрицательное целое, являющееся числом решений задачи (например, число гамильтоновых циклов в графе или число совершенных паросочетаний).

Пусть Z — некоторая перечислительная задача, I — вход задачи. Пусть далее #(I) обозначает число различных решений для входа I задачи Z.

Определение 4.2.1. Пусть

Z — перечислительная задача.

I — вход для Z, n = jIj.

#(I) — число различных решений для входа I задачи Z.

» > 0 — параметр точности.

Вероятностный алгоритм A(I; «) — полиномиальная рандомизированная аппроксимационная схема, если время его работы ограничено полиномом от n, и

P[(1 «)#(I) A(I; «) (1 + «)#(I)] 34:

4.2. ВЕРОЯТНОСТНЫЕ МЕТОДЫ

В ПЕРЕЧИСЛИТЕЛЬНЫХ ЗАДАЧАХ

163

Определение 4.2.2. Полностью полиномиальной рандомизированной аппроксимационной схемой (FPRAS)

называется полиномиальная рандомизированная аппроксимационная схема, время работы которой ограничено полиномом от n и 1/«.

Определение 4.2.3. Полностью полиномиальной рандомизированной аппроксимационной схемой с па-

раметрами («; ) (или кратко («; )-FPRAS) для перечислительной задачи Z называется полностью полиномиальная рандомизированная аппроксимационная схема, которая на каждом входе I вычисляет «-аппроксимацию для #(I) с вероятностью не менее 1 за время, полиномиальное от n, 1/«

и log 1/ .

Рассмотрим теперь одну перечислительную задачу.

Задача 18. f(x1; : : : ; xn) = C1_ : : :_Cm — булева формула в дизъюнктивной нормальной форме (ДНФ), где каждая скобка Ci есть конъюнкция L1 ^ : : : ^ Lki ki литералов (см. определение 3.3.1 «Литерал»).

Набор v = (v1; : : : ; vn) — выполняющий для f, если f(v1; : : : ; vn) = 1.

Найти число выполняющих наборов для данной ДНФ.

Пусть

V — множество всех двоичных наборов длины n.

G — множество выполняющих наборов.

Рассмотрим алгоритм, основанный на стандартном методе Монте-Карло, и покажем, что он не является («; )-FPRAS для этой задачи.

1. Проведем N независимых испытаний:

164

Глава 4. ВЕРОЯТНОСТНЫЕ АЛГОРИТМЫ И ИХ АНАЛИЗ

•выбирается случайно v 2 V (в соответствии с равномерным распределением);

•yi = f(vi). Заметим, что Pfyi = 1g = jjVGjj . Обозначим эту вероятность через p.

2.Рассмотрим сумму независимых случайных величин Y = ∑Ni=1 yi. В качестве аппроксимации jGj возьмем величину

~ Y

G = N jV j:

Упражнение 4.2.1. Почему yi независимые случайные величины?

Воспользуемся следующей леммой.

Лемма 15. Пусть x1; : : : ; xn — независимые случайные величины, такие, что xi принимают значения

0; 1, и P fxi = 1g = p, P fxi = 0g = 1 p. Тогда для X =

in=1 xi и для любого 0 < < 1, выполнено

неравенство

∑

2

/3) E Xg:

P fjX

E Xj > E Xg 2 expf

(

Доказательство леммы изложено в [MR95].

Оценим вероятность того, что аппроксимация хорошая:

~

Pf(1 «)jGj G (1 + «)jGjg =

NjGj

NjGj

=

Pf

(1 «)

Y

(1 + «)

g

=

j

V

j

j

V

j

= Pf(1 «)Np Y (1 + «)Npg:

4.2. ВЕРОЯТНОСТНЫЕ МЕТОДЫ

В ПЕРЕЧИСЛИТЕЛЬНЫХ ЗАДАЧАХ

165

Применяя неравенства из леммы, получаем:

~

2

/3)Npg:

Pf(1 «)jGj G (1 + «)jGjg > 1

2 expf («

Потребуем, чтобы эта вероятность хорошей аппроксимации была 1 , тогда получим

«

2Np

2 exp {

} < ;

3

2

< exp {

«2Np

} ;

3

N >

1 3

ln

2

:

p «2

Почему полученная оценка не столь хороша? Потому что p может быть экспоненциально мало (например, если функция равна 1 лишь в одной точке), и тогда число требуемых шагов будет экспоненциально велико.

Покажем, как использовать этот же метод не напрямую, а после некоторой модификации задачи ([KLM89]). Рассмотрим более общую (по сравнению с задачей о числе выполняющих наборов) задачу.

Задача 19. Пусть V — конечное множество, и имеется m его подмножеств H1; : : : ; Hm V , удовлетворяющих следующим условиям:

1. 8i jHij вычислимо за полиномиальное время.

2. 8i возможно выбрать случайно и равномерно элемент из Hi.

166

Глава 4. ВЕРОЯТНОСТНЫЕ АЛГОРИТМЫ И ИХ АНАЛИЗ

?

3. 8v 2 V за полиномиальное время проверяемо «v 2 Hi».

Рассмотрим объединение H = H1 [ : : : [ Hm. Надо оценить его мощность jHj.

Связь с исходной задачей 18:

«V »: базовое множество V состоит из всех двоичных наборов длины n.

«Hi»: Hi = fv 2 V : Ci(v) = 1g, т. е. состоит из всех наборов, на которых скобка Ci равна 1 (выполнена).

Условие (1): Пусть ri — число литералов в Ci, тогда:

{

Ci 0 ) jHij = 0; Ci ̸ 0 ) jHij = 2n ri :

Условие (2): Cлучайная выборка элемента из Hi — зафиксировать переменные из Ci, а остальные переменные выбрать случайно.

Условие (3): вычислить Ci(v), т. е. проверка, что некоторое v 2 V принадлежит Hi, эквивалентно проверке выполнимости скобки (конъюнкции) на данном наборе.

Идея, позволяющая предложить для рассматриваемой задачи FPRAS, проста. Мы определим относительно небольшой универсум, подмножеством которого будет H = H1 [ : : : [ Hm. Универсум U образуется из точек H, причем точка берется с кратностью, равной числу множеств Hi, которым она принадлежит. Тогда

∑

∑i

m

1

m

1

jUj =

jHij jHj

m

=1

jHij =

m

jUj;

i=1

4.2. ВЕРОЯТНОСТНЫЕ МЕТОДЫ

В ПЕРЕЧИСЛИТЕЛЬНЫХ ЗАДАЧАХ

167

DNF = (x3 x4 x1) _ (x1 x4) _ (x4 x2) _ (x3 x4 x2) _ (x3 x2)

x1

x2

x3

x4

C1

C2

C3

C4

C5

ДНФ

0

0

0

0

1

0

0

0

0

1

0

0

1

1

0

0

0

0

1

0

■

□

1

1

0

1

0

■

1

0

1

1

0

■

1

1

1

1

0

0

0

0

1

■

1

1

0

0

1

■

□

1

0

1

0

1

1

1

0

1

■

1

0

0

1

1

■

□

□

1

1

0

1

1

■

□

□

□

1

0

1

1

1

1

1

1

1

■

1

•По вертикали — бинарные наборы v.

•U = f(v; i)j v 2 Hig, элементы соответствуют квадратикам на рисунке. jUj = ∑mi=1 jHij jHj.

•cov(v) = f(v; i)j (v; i) 2 Ug (квадратики на строчке v), cov(v) m.

∑

• U = [v2H cov(v), jUj = v2H jcov(v)j.

168 Глава 4. ВЕРОЯТНОСТНЫЕ АЛГОРИТМЫ И ИХ АНАЛИЗ

и к U можно применять стандартный алгоритм Монте-Карло.

Конкретно для нашей задачи 18 «DNF#» определения и иллюстрация множеств U и H показаны на рис. 4.1. Наша цель теперь заключается в оценке мощности G U, для чего мы применяем метод МонтеКарло к множеству U:

1. Выбираем случайно и равномерно u = (v; i) 2 U:

(a) выберем i, 1 i m с вероятностью

jHij

=

mjHij

;

jUj

∑i=1 jHij

(b)выбирается случайно и равномерно v 2 Hi.

2.yi = 1 при v 2 G, иначе yi = 0.

3.Y = ∑Ni=1 yi.

Теорема 14. Метод Монте-Карло дает («; )-FPRAS для оценки jGj при условии

N 3«m2 ln 2:

Время полиномиально по N.

Доказательство. Выбор случайного элемента (v; i) из U происходит равномерно из U — для доказательства достаточно перемножить соответствующие вероятности.

?

Проверка (v; i) 2 G — полиномиальна: 8j < i : Cj(v) = 0.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Понравилась статья? Поделить с друзьями:

Не пропустите эти материалы по теме:

  • Яндекс еда ошибка привязки карты
  • Вероятность отсутствия ошибок отбора единиц исследования это
  • Вероятность определения ожидаемой ошибки
  • Вероятность необнаруженной ошибки
  • Вероятность неисправленной ошибки

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии