Вероятность ошибки crc32

Вначале хочу заметить, если вы задаетесь таким вопросом, то скорее всего вы используйте функцию чек-суммы не по прямому назначению. А значит, вы делаете что-то неправильно.

Насколько я понял, вам интересно, одинаков ли шанс получить коллизию, если на входе строка из букв, или строка из цифр. Хочу заметить, что если у вас откуда-то приходят случайные строки длиной 5 символов (для примера), то шанс что у вас появятся одинаковые строки из цифр на много-много порядков выше, чем когда приходят строки из букв.

Что бы показать, что шансы получить коллизию одинаковы, я сгенерировал 100 млн чек-сумм для строк длиной 20 (я взял 20, что бы не создавались одинаковые строки из чисел), и посчитал коллизии внутри строк из чисел, внутри строк из букв, и взаимные коллизии между строками из чисел и букв. Вот мой код на C#:

private static uint crc32(byte[] data)
{
    uint crc = 0xffffffff;
    uint poly = 0xedb88320;
    for (int i = 0; i < data.Length; i++)
    {
        uint c = (crc ^ data[i]) & 0xff;
        for (int k = 0; k < 8; k++)
            c = (c & 1) != 0 ? poly ^ (c >> 1) : c >> 1;
        crc = c ^ (crc >> 8);
    }
    return crc ^ 0xffffffff;
}

static void Main(string[] args)
{
    byte[][] digits = new byte[0x10000][];
    for (int i = 0; i < 0x10000; i++)
        digits[i] = new byte[0x10000];

    byte[][] chars = new byte[0x10000][];
    for (int i = 0; i < 0x10000; i++)
        chars[i] = new byte[0x10000];

    var rnd = new Random(123);
    int iterations = 100000000;

    byte[] buffer = Encoding.ASCII.GetBytes("12345678901234567890");
    for (int i = 0; i < iterations; i++)
    {
        int index = rnd.Next(20);
        buffer[index]++;
        if (buffer[index] > '9')
            buffer[index] = (byte)'0';

        uint crc = crc32(buffer);
        digits[crc >> 16][crc & 0xFFFF]++;
    }

    buffer = Encoding.ASCII.GetBytes("abcdefwxyzabcdefwxyz");
    for (int i = 0; i < iterations; i++)
    {
        int index = rnd.Next(20);
        buffer[index]++;
        if (buffer[index] > 'z')
            buffer[index] = (byte)'a';

        uint crc = crc32(buffer);
        chars[crc >> 16][crc & 0xFFFF]++;
    }

    int digitsCollisions = 0;
    for (int i = 0; i < 0x10000; i++)
        for (int j = 0; j < 0x10000; j++)
            if (digits[i][j] > 1)
                digitsCollisions += digits[i][j];

    int charsCollisions = 0;
    for (int i = 0; i < 0x10000; i++)
        for (int j = 0; j < 0x10000; j++)
            if (chars[i][j] > 1)
                charsCollisions += chars[i][j];

    int digitsCharsCollisions = 0;
    for (int i = 0; i < 0x10000; i++)
        for (int j = 0; j < 0x10000; j++)
            if (chars[i][j] > 0 && digits[i][j] > 0)
                digitsCharsCollisions += chars[i][j] * digits[i][j];

    Console.WriteLine(digitsCollisions);
    Console.WriteLine(charsCollisions);
    Console.WriteLine(digitsCharsCollisions);
}

Результат:

2298490
2304243
2330855

Как видно, вероятность получить коллизию одинаковая.

В другом тесте я брал длину входных данных 10 байт, и вместо случайных чисел просто брал строковое представление числа i. Результат получился другой:

4431872
2301156
2324554

Как видно, коллизий на числах в 2 раза больше, хотя чек-сумма считалась на уникальных входных данных. Это происходит потому, что в случайной строке из букв длиной 10 байт больше энтропии, чем в строке чисел. CRC-32 не является полноценной криптографической хеш-фукнцией, и в ней нет лавинного эффекта. С хорошей хеш-функцией мы бы получили одинаковый результат.

Источник

$begingroup$

I have a table which stores all serial numbers of devices in my system:

|------------------------|--------------------------|
|            #           |  Serial number (4 bytes) |
|------------------------|--------------------------|
|            1           |        0x????????        |
|------------------------|--------------------------|
|            2           |        0x????????        |
|------------------------|--------------------------|
|           ...          |            ...           |
|------------------------|--------------------------|
|           31           |        0x????????        |
|------------------------|--------------------------|

If I add a device to the system the position in the table is not predictable. If something in the system changes (e.g. add one or more devices, remove one or more devices, replace a device) I want to detect with a «high» propability that the system change. Therefor I want to use a CRC-32. In my system I have at least always 2 devices but max. 31 devcies. Meaning that the input of the CRC can vary between $2^{64}$ to $2^{992}$ different input streams.

As far as I understand:

The minimum input should be at least 32 bits
The most important is to use the right generator polynom. E.g.:
- CRC-32
- CRC-32-IEEE
- CRC-32C
The selection of generator polynom depends on:
- Input stream length
- Error-detection-feasability
- Collision probablility
Detection of a single bit error: All CRC’s can do this
Detection of burst errors: All $n$-bit CRC’s can detect burst errors up to $n$ consecutive bits. Also meaning appending new $n$-bit to the end of the input stream.

My concerns are the collision probability of the CRC32 is to high and due to that I don’t detect a change in the configuration. Therefor I want to calcualte this probabilities and my questions are:

Is CRC the right method to use for my use case? If not what would be the best?
What is the «best» generator polynom for my use case?
How to cacluate the error-detection-feasability or collision probability if more then 32 consecutive bits change?
How to cacluate the error-detection-feasability or collision probability if $x$ not consecutive (different locations in the complete input stream) bits change?

Raphael♦

71.7k27 gold badges175 silver badges382 bronze badges

asked Jan 10, 2018 at 17:52

$endgroup$

$begingroup$

There’s nothing in your requirements that forces you to use a CRC32. You could use any checksum. If the collision probability for a CRC32seems too high, use a different checksum.

For instance, if you use SHA256, you will never have to worry about collisions — for all engineering purposes, you can treat them as impossible (something that will never happen in your lifetime). And then you won’t need to worry about selecting generator polynomials or anything like that; someone else has done all that work for you. You just use the standard SHA256 algorithm.

P.S. Using a basic checksum algorithm will require you to recompute the checksum on the entire table any time you insert or delete one row. If that’s too slow, there are a number of schemes to speed that up, such as a Merkle hash tree.

answered Jan 10, 2018 at 22:16

D.W.♦D.W.

152k19 gold badges214 silver badges440 bronze badges

$endgroup$

Источник

Задачка.

1. полное отсутствие ошибок при передаче инфы в пакете(ах) низкоскоростного канала связи (30-200 кб/c);

2. алгоритмы и полиномы восстановления битовых искажений не интересуют;

3. математики и криптоаналитики, судя по гугл-анализу говорят — CRC32 фигня.
Для 100%контроля полной целостности пакетов не годятся, есть реальная вероятность такого искажения бит-потока, пакета, когда CRC32 даст НОРМУ! А это НЕДОПУСТИМО!

4. решение — пакет передается всегда равными блоками, никакой CRC не использовать, он просто шифруется, допустим AES-256 на передаче, ключ известен на приемной и передающей стороне. Сбой=отсутствие дешифрации пакета, для этого внутри пакета, помимо данных закладываем опознавательную сигнатуру, ну и некий сетевой номер, пусть это некий аналог IP.

Совсем неясно, не занаю, как доказать (математически ну очень желательно) невозможность прохождения ложного (сбойного искаженного) пакета на приемной стороне?
Вот про то, как невозможно, проблемно, сложно подобрать ключ, вероятность этого дела к разным криптоалгоритмам читал, находил, а как Вам задачка, так сказать с другой стороны?
Аналогов не видел. Может ссылку дадите или разрулите сходу, что данное решение верно?
737061

New Member

Публикаций:

0

Регистрация:

3 авг 2007

Сообщения:

74

VaStaNi
Я не совсем вкурил в задачу, но чебы не использовать какой-нибудь «сильный» хэш для каждого пакета, и соответственно вероятность «ошибки» будет настолько низка по определению этого алгоритма, что можно считать ее равно 0.
а чем AES-256 не сильный хеш???
допустим у меня 32 байта блок, в нем 24 байта DATA, а отстальное, добавочки, что говорил.
Пропускаем через AES-256, далее «выплюнул» в канал.
КАК ДОКАЗАТь, что приемник НИКОГДА не подхватит ЛОЖЬ?
НУ пусть для злобы дня и темы ,перед глазами Япония и ее АЭС управление представится
Не моделировать годами в подхвате сбоя!? А как вероятность показать?
ЗЫ
тут про AES так пишутhttp://diskcryptor.net/wiki/CryptoUsageRisks
Поэтому стойким считается тот шифр, для которого пока что не придумали практичного метода взлома. Однако если такого метода ещё не придумали, то это не значит что его не придумают никогда, хотя применительно к хорошо изученным шифрам (AES, Twofish, Serpent) вероятность взлома в ближайшие 10 лет пренебрежительно мала.
737061

New Member

Публикаций:

0

Регистрация:

3 авг 2007

Сообщения:

74

VaStaNi
ну смотри. надо просто посмотреть какова вероятность что при сбое биты изменятся так что хэш получится правильный. Я тебе сразу говорю что вероятность -> 0. Как доказывать мат корректно я не помню, но думаю надо рассмотреть условные вероятности для битов те P(h(1)=x1,…,h(n)=xn | d(z)=L) h хэш d данные, те мы смотрим вероятность что хэш получится правильный для измененных данных (x1,x2,..,xn) при условии что на z позиции произошел сбой, но я еще раз повторяю она стремится к 0, просто следует из «сильности» хэша. Возможно пишу бред, криптографией не когда не занимался делаю прикидки на основе тер вера.
737061

New Member

Публикаций:

0

Регистрация:

3 авг 2007

Сообщения:

74

А вот насчет никогда ответ простой НИКАК. Просто вероятность будет стремится к 0, на самом деле этого достаточно.
Да и я никогда не занимался и тем более настолько математически не покажу…
Ну а показать выкладки хотелось бы, дабы сторонний суперматематический ум там некий, проверочные организации там всякие приняли однозначный вывод да стремится к нулю и на 100000…. лучше чем … … … и CRC32, который вот тут вот …., а ЭТО ДАННОЕ РЕШЕНИЕ — достойная модернизация ….
Ну и самому спать спокойно, тоже нужно, зачем лишнее на себя брать
artkar

New Member

Публикаций:

0

Регистрация:

17 авг 2005

Сообщения:

400

Адрес:

Russia

А што это такое?

Во! Сила 737061
OLS

New Member

Публикаций:

0

Регистрация:

8 янв 2005

Сообщения:

322

Адрес:

Russia

О чем же всё таки вопрос ?

Сколько бит необходимо для гарантии незначимости вероятности ошибки ?

Возьмите суммарную пропускную способность Ваших каналов (например, 16 х 200 кбит/с = 3.2 Мбит/с).
Выберите период, на который Вы сделаете прогноз (например, 5 лет) — на бесконечность Вам никогда не дадут, т.к. есть экспоненциальное
увеличение мощностей и пропускных способностей — даже документы по стойкости шифров рассчитываются на определенный весьма небольшой период.
Рассчитайте, сколько пакетов по 32 байта будет передано, если использовать этот канал этот период времени со 100% загрузкой — (3.200.000/8/32*3600*24*365*5)=2^41 штук.
Задайтесь, приемлемой вероятностью события — например 0,001 — т.е. «это вероятность того, что за 5 лет в используемых каналах связи будет хотя бы однажды не обнаружено повреждение переданных данных».
И получите : 41 бит + 10 бит = 51 бит контрольной суммы необходимы Вам в каждом 32-байтном пакете для решения Вашей задачи.

или

Может ли внутри контейнера, защищенного блочным шифром, использоваться обычная CRC для контроля целостности (без угроз подделки CRC извне) ?

Я считаю, что может, если у Вас есть ограничения по вычислительным мощностям и Вы не можете позволить по-настоящему криптостойкую сумму. Но если ключ шифрования фиксированный, то серьезно подумайте о методе создания цепочек (chaining modes), т.к. на мой взгляд OFB или CFB здесь будут не очень удачным решением. CBC — наверное, да, а лучше всего сразу искать цепочки со встроенным подтверждением целостности — таких уже разработано за последние годы много.

А если содержимое пакетов однотипно, то защищайтесь еще и от replay attack, иначе Ваши пакеты не дешифруя могут «подкинуть» в канал через определенное нужное злоумышленнику время повторно.
ближе второе. Сейчас попытаюсь изложить и сформулировать еще раз

ну вот тут вижу как бы что это лишнее(в смысле CRC внутри, это же доп.затраты? А эффект?), хотя если это совет, как грамотного криптоаналитика, то прислушаюсь…

можно сказать и ограничения есть, т.к. вторая сторона пусть управляющие контроллеры АСУТП, пусть на AVR контроллерах, хотя и на других можно. Есть уже (нашел) сорцы ассемблерные AES на них в реализации! Режимы там всякие CFB, OFB пока смутно понимаю, вкуривать пытаюсь…
Надеюсь помогут вот тут. Ну хоть ткнуть, конктерно поняв мою задачу(ниже).
Типа тебе вот типа CFB надо, ключ не менее… будет толк и точка.

где то толковое почитать есть? Сориенироваться не могу, что мне лучше в них, какой вот?

в AES это достижимо? Опять же сорцы есть, хочется не заморачиваться. Кто такие, где читать если нет в нем этого?

ну про «подкинуть», как бы не ставится задачка защищаться
Хотя если учитывать всякое там перемешивание бит в крипто, то можно в пакетик данных счетчик времени, даты текущий ставить или некое время жизни пакета, как в TCP… тогда это устраняется, да? Я в нужном русле решаю проблемс этот?
ИТАК.
1. Пусть необходимо максимально достоверно передать блок данных конкретному устройству в некой низкоскоростной сети. Таких устройств пусть их 30 шт. Полудуплекс. Блок данных унифицирован, т.е. известен его формат внутри, длина постоянна, пусть это 32 или 64 или 128 байт, пока решаю, как дробить на фрагменты, так сказать элементарных достоверных передач! Есть там и сетевой номер и сигнатура (будет ли верно это?) по которой собственно + номер этот сетевой — устройство понимает решение(!), что пакет дешифрирован ВЕРНО и ДАННЫЕ — это его данные! Тогда принимаем данные за абсолютную истину и ВЫПОЛНЯЕМ свою функцию по ним!
Ни чужое(другого устройства), ни искаженное типа молниями, облучениями, ни магнитными бурями ни чем другим, не должно быть принято к исполнению!

2. Пусть выбрано, также, что блоки эти шифруются/дешифруются AES-256 с известным ключём по всем сетевым точкам (устройствам, включая хост или комп.)

Понятно, что идеального в нашем несовершенном мире ничего нет, но!
Вопрос тут в максимально достижимости устойчивости данных (ну и системы вцелом, естественно) ПОСРЕДСТВОМ КРИПТОалгоритмики, как более совершенного средства защиты целостности информации и распознания фальши(сбоев)!
Понимаю так, что чем круче крипто, тем более «чувствуется» искажение любого бита в любом месте пакета в данном случае, а значит ЛОЖЬ(сбой) не пройдет, или максимально НЕ пройдет. Понятно и то, что чем лучше базовые принципы — тем лучше итог, но как, насколько не могу оценить, показать, доказать… Чувствовать мало.
Может и так быть, думаю, что длина пакета влияет на результат и длина ключа(это понятно в принципе) и неоднородность данных на выявление ложного случая(сбоя)…
С удовольствием выслушаю взвешенные под задачу советы, замечания, мои заблуждения быть может.
artkar

New Member

Публикаций:

0

Регистрация:

17 авг 2005

Сообщения:

400

Адрес:

Russia

Если у тебя блок из 24 байтов, то тагда количество комбинаций равно 2^(8*24), для ЦРЦ 32 количество элементов в списке коллизий, при условии канешн што твой пакет (24 байта) не меняет размер, равно 160 — это значит в этом блоке возможно столько комбинаций которые дадут одинаковый ЦРЦ, следовательно вероятность пропущения ошибки равна 160/2^(8*24) это колосальное число у меня даже не влазит в калькулятор 2.5489470578119236432462086364286e-56, Но если тебя и эта вероятность не устраивает тагда можно взять для ЦРЦ другой порождающий полином G(x), равный допустим 24 байтам, тогда теоритически вероятность равна нулю, но! нужно учесть что и полином может так измениться что совпадет битый ЦРЦ с битыми данными, но вероятность просто фантастически маленькая, но всё же не ноль!
вот этот математически доказуемый факт очень не нравится. Потенциально. При том, что на тех же аппаратно-программных средствах, можно сделать и лучше, и устойчивее, и жестче. Т.к. доверять будем лишь одному — факту успешной дешифрации принятого пакета.
Вот еще интересный для себя под задачку алгорим присмотрел — ANUBIS. Вики говорит

Тут опять пишут ТОЛЬКО про уязвимость со стороны ключа. Непонятно вот почему про сами данные ни словца. Либо с данными (мутации всякие, перестановки, комбинаторика) все еще более серьезно обстоит и это даже НЕ обсуждается и НЕ доказывается в плане безопасности(и это типа только мне не понятно, а остальным все и так ясно, как Божий день), либо так сложно, что нет смысла этим заниматься… годы нужны для этого?
Ну вот типа инволюции обратимы, написано. Это для аппаратуры типа просто для реализации, я так понял. А как это на устойчивости сказывается неясно. Лучше это скажем AESа или нет? Или это «на пальцах» не покажешь, суровая математика нужна…
Может тут все банально получается. И если для ключа(со стороны ключа) нужно 2^127 комбинаций, допустим, то «автоматически» это означает, что для данных это значение НЕ МЕНЬШЕ? Или не факт?????
asmlamo

Well-Known Member

Публикаций:

0

Регистрация:

18 май 2004

Сообщения:

1.722

>1. полное отсутствие ошибок при передаче инфы в пакете(ах) низкоскоростного канала связи

Любая нормальная хеш функция.

Если задача именно о ошибках а не о злонамеренном вмешательстве.
VaStaNi
В сообщении #9 OLS вроде бы достаточно ясно изложил суть, но вот анекдот по данной теме:
Какова вероятность встретить на улице динозавра?
1/2 — либо встречу, либо нет.
В общем тебе нужно рассуждать точно так же, если от блока данных вычислить хорошую хеш функцию длиной n бит, то все её значения сделует считать равновероятными, а вероятность что у искажённого сообщения окажется такой же хеш — 1/2^n. Если количество переданных сообщений N существенно меньше 2^n, то вероятность незамеченной ошибки можно считать равной N/2^n.
Black_mirror, спасибо за рассуждения

ну вот пытаюсь определиться с понятием «хорошая» следующим образом.
Получается у меня, обобщив посты следующее:
1. чем меньше блок и чем больше ключ тем лучше
2. длина пакета передачи не может быть меньше блока шифрования и очень хорошо если кратна им.
Дополнение данных дописыванием байт до кратности блоку лишь улучшает достижение цели, особенно если дописывание имеет динамику и информационный, справочный смысл функционирования (текущее время передачи пакета, например)
3. по рекомендациям OLS, лучше использовать CBC mode, но при длине пакета = 1-2 блока шифрования его преимущества теряются, глядя сюда
4. при равенстве степеней полиномов в AES и Anubis, Anubis видится более выгодным под задачу, т.к. можно заюзать по п.1 ключ в 320 бит при блоке в 128 бит, возможно при этом будет плюсом, что выбор в пользу tweak для чипов малой мощности даст плюс, как упрощение в реализации программного кода…
Если есть существенные заблуждения, неправильная оценка и ошибки, просьба указать.
PS.
Всмотревшись в блок-схемы по CBC «вижу» сетевой номер и пр. ID устройства типа серийный номер изделия… в таком чудесном блочке как: «вектор инициализации». Если это будет работать, тогда только CBC! Крутой битовый замес, а-ля «белый шум»…
Вижу это, как МегаФичу при решении задачи… несладко придется хосту однако, но все для победы!
OLS

New Member

Публикаций:

0

Регистрация:

8 янв 2005

Сообщения:

322

Адрес:

Russia

Если у Вас есть проблемы с вычислительной сложностью, возьмите
в качестве блочного шифра — ГОСТ 28147-89
в качестве контрольной суммы любые 8 байт от MD2.

В качестве IV в схеме CBC лучше подавать не сырые данные (время, номер пакета, сетевой номер, ID и т.п.), а уже прошедшие один цикл шифрования, чтобы убрать любые корреляции. Учтите, что IV приемная сторона должна иметь возможность узнать/вычислить, т.е. все ее части должны быть несекретными и каким-то образом передаваться на приемную сторону.
Винокуров пишет в сравнительной статье, что и ГОСТ и AES почти равны по всем статьям включая 8 битки для выполнения алгоритма… Конечный выбор видимо будет судя по сложности воплощения в жизнь в железе.

это типа MAC? Или это с «другой песни»? ) Мне уже от аббревиатур этих в глазах рябит и череп сносит, начитался этой пурги…)))
Или тут должен быть иной алгоритм (совсем не «родной») для первичного, так сказать преобразования открытых известных значений типа ID для получение этого вектора инициализации?
В виках:
OLS

New Member

Публикаций:

0

Регистрация:

8 янв 2005

Сообщения:

322

Адрес:

Russia

Я предлагал просто пройтись один раз тем же самым криптоалгоритмом тем же самым ключом по открытым данным, которые Вы планируете использовать в качестве IV, для того, чтобы убрать возможную явную корреляцию между битами IV (ведь с схеме CBC он (IV) накладывается на первый блок обычным XOR-ом).
Вернулся к расчету вероятности. Хотябы ориентировочный, оценочный расчет, опираясь на пост #14 вижу так.

— пусть, например, битовый объем данных = ключу = хешу = 128 бит

— вероятность НЕОБНАРУЖЕННОЙ ошибки НЕ белее чем 128 / 2^128 = 3,76 E-37, что практически ноль.

Учитывая, что в процессе очень ответственных управленческих задач АСУ ТП хост, как правило, не ограничивается одним управляющим пакетом(приказ выполнить управление, регулирование), а требует замыкающего ответного квитирования от подчиненного(как ответ «ЕСТЬ мой генерал!»), то в итоге можно считать цель достигнутой. Т.е. 100% гарантия построения надежной системы идеологически достигнута, сабж можно считать исчерпаным.

Источник

: January 25 2003, 02:16

Category:

Быт
Cancel

Как оценить веротяность того, что хэш, посчитанный по алгоритму CRC32 для двух различных строк ASCII символов, будет одинаковым? Для определенности предположим, что максимально может быть 25000 различных строк, где каждая строка состоит максимум из 32 символов, каждый из которых попадает в диапазон [0x20; 0x5f].

Насколько будет близка к правде величина 25000/(2^32)? Порядок величины будет тот же или может отличаться на, скажем, три порядка?

Источник

2004 г.

2.7. Обнаружение ошибок

Семёнов Ю.А. (ГНЦ ИТЭФ), book.itep.ru

Каналы передачи данных ненадежны, да и само оборудование обработки информации работает со сбоями. По этой причине важную роль приобретают механизмы детектирования ошибок. Ведь если ошибка обнаружена, можно осуществить повторную передачу данных и решить проблему. Если исходный код по своей длине равен полученному коду, обнаружить ошибку передачи не предоставляется возможным.

Простейшим способом обнаружения ошибок является контроль по четности. Обычно контролируется передача блока данных (М бит). Этому блоку ставится в соответствие кодовое слово длиной N бит, причем N>M. Избыточность кода характеризуется величиной 1-M/N. Вероятность обнаружения ошибки определяется отношением M/N (чем меньше это отношение, тем выше вероятность обнаружения ошибки, но и выше избыточность).

При передаче информации она кодируется таким образом, чтобы с одной стороны характеризовать ее минимальным числом символов, а с другой – минимизировать вероятность ошибки при декодировании получателем. Для выбора типа кодирования важную роль играет так называемое расстояние Хэмминга.

Пусть А и Б две двоичные кодовые последовательности равной длины. Расстояние Хэмминга между двумя этими кодовыми последовательностями равно числу символов, которыми они отличаются. Например, расстояние Хэмминга между кодами 00111 и 10101 равно 2.

Можно показать, что для детектирования ошибок в n битах, схема кодирования требует применения кодовых слов с расстоянием Хэмминга не менее N+1. Можно также показать, что для исправления ошибок в N битах необходима схема кодирования с расстоянием Хэмминга между кодами не менее 2N+1. Таким образом, конструируя код, мы пытаемся обеспечить расстояние Хэмминга между возможными кодовыми последовательностями больше, чем оно может возникнуть из-за ошибок.

Широко распространены коды с одиночным битом четности. В этих кодах к каждым М бит добавляется 1 бит, значение которого определяется четностью (или нечетностью) суммы этих М бит. Так, например, для двухбитовых кодов 00, 01, 10, 11 кодами с контролем четности будут 000, 011, 101 и 110. Если в процессе передачи один бит будет передан неверно, четность кода из М+1 бита изменится.

Предположим, что частота ошибок (BER) равна р=10^-4. В этом случае вероятность передачи 8 бит с ошибкой составит 1-(1-p)⁸=7,9х10^-4. Добавление бита четности позволяет детектировать любую ошибку в одном из переданных битах. Здесь вероятность ошибки в одном из 9 бит равна 9p(1-p)⁸. Вероятность же реализации необнаруженной ошибки составит 1-(1-p)⁹ – 9p(1-p)⁸ = 3,6×10^-7. Таким образом, добавление бита четности уменьшает вероятность необнаруженной ошибки почти в 1000 раз. Использование одного бита четности типично для асинхронного метода передачи. В синхронных каналах чаще используется вычисление и передача битов четности как для строк, так и для столбцов передаваемого массива данных. Такая схема позволяет не только регистрировать но и исправлять ошибки в одном из битов переданного блока.

Контроль по четности достаточно эффективен для выявления одиночных и множественных ошибок в условиях, когда они являются независимыми. При возникновении ошибок в кластерах бит метод контроля четности неэффективен и тогда предпочтительнее метод вычисления циклических сумм (CRC). В этом методе передаваемый кадр делится на специально подобранный образующий полином. Дополнение остатка от деления и является контрольной суммой.

В Ethernet Вычисление crc производится аппаратно (см. также ethernet). На рис. 2.7.1. показан пример реализации аппаратного расчета CRC для образующего полинома B(x)= 1 + x² + x³ +x⁵ + x⁷. В этой схеме входной код приходит слева.

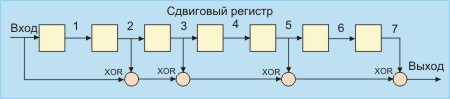
Рис. 2.7.1. Схема реализации расчета CRC

Эффективность CRC для обнаружения ошибок на многие порядки выше простого контроля четности. В настоящее время стандартизовано несколько типов образующих полиномов. Для оценочных целей можно считать, что вероятность невыявления ошибки в случае использования CRC, если ошибка на самом деле имеет место, равна (1/2)^r, где r — степень образующего полинома.

CRC-12	x¹² + x¹¹ + x³ + x² + x¹ + 1
CRC-16	x¹⁶ + x¹⁵ + x² + 1
CRC-CCITT	x¹⁶ + x¹² + x⁵ + 1

Назад: 2.6.5. Статический алгоритм Хафмана
Оглавление: Телекоммуникационные технологии
Вперёд: 2.8. Коррекция ошибок

Источник

737061

New Member

737061

New Member

737061

New Member

artkar

New Member

OLS

New Member

artkar

New Member

asmlamo

Well-Known Member

OLS

New Member

OLS

New Member

2.7. Обнаружение ошибок

Не пропустите эти материалы по теме:

737061 New Member

737061 New Member

737061 New Member

artkar New Member

OLS New Member

artkar New Member

asmlamo Well-Known Member

OLS New Member

OLS New Member

2.7. Обнаружение ошибок

Не пропустите эти материалы по теме:

737061

New Member

737061

New Member

737061

New Member

artkar

New Member

OLS

New Member

artkar

New Member

asmlamo

Well-Known Member

OLS

New Member

OLS

New Member