Введение
Моя сеть приёма сигналов со спутников r2cloud постепенно растёт. Однако уровень приёма оставляет желать лучшего. Несмотря на то, что на спектограмме виден сигнал, демодулятор не может восстановить его. В попытках найти проблему, я понял, что мне не хватает фундаментальных знаний по теории обработки сигналов и некоторой математики. Дело в том, что в интернете зачастую выкладываются демодуляторы без обоснования их работы. Меня это не устраивает, потому что нужны метрики по которым я буду понимать насколько один алгоритм эффективнее другого. И стал ли новый код лучше, если я добавлю какой-нибудь другой блок в обработку.
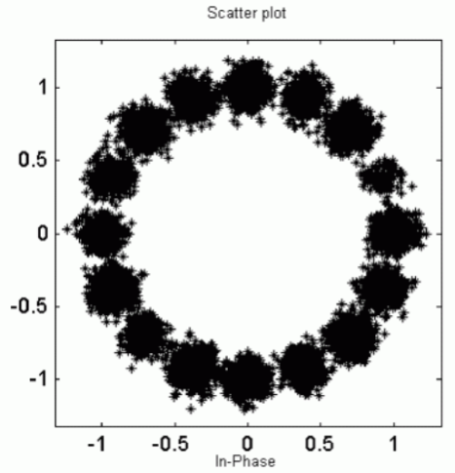
Всё это привело меня к ( E_b / N_0 ). Эта метрика показывает отношение энергии сигнала, приходящейся на 1 бит принимаемого сообщения (( E_b )), к энергетической спектральной плотности шума (( N_0 )). Почему она так важна? Дело в том, что она не зависит от способа модуляции сигнала и пропускной способности канала. Из-за этого её можно использовать, чтобы сравнивать различные модуляции между собой. Обычно строят график отношения ( E_b / N_0 ) к вероятности ошибки (BER). Вот пример графика сравнения BPSK/QPSK/8-PSK/16-PSK:
Что из этого графика можно понять?
- Если увеличивать энергию передаваемого бита, то уменьшается вероятность возникновения ошибки.
- В BPSK/QPSK ошибка возникает значительно реже, чем в 8-PSK и 16-PSK при одинаковых значениях энергии передаваемого бита.
- График, например, читается следующим образом: при ( E_b / N_0 ) равным 4 децибелла и BPSK модуляции можно получить 1 ошибочный бит на каждые 100 полученных.
Мне же график прежде всего нужен:
- Сравнивать теоретические значения с практической реализацией демодулятора. Прямо сейчас я точно знаю, что различия есть из-за ограниченной точности АЦП. Дело в том, что rtl-sdr имеет разрешающую способность 8 бит. А в теории числа могут быть бесконечной точности. Именно эта разница и должна давать ошибку.
- Анализировать улучшится ли демодулятор, если добавить какой-то определённый блок. Как минимум я хочу попробовать различные алгоритмы получения несущего сигнала и компенсации многолучевого распространения.
Ну и для того, чтобы понять математику, я решил проделать выводы сам. Ниже я буду рассчитывать вероятности ошибки для BPSK (см. синий график выше). Вдохновение я черпал у dsplog плюс добавлял свои мысли.
Дано
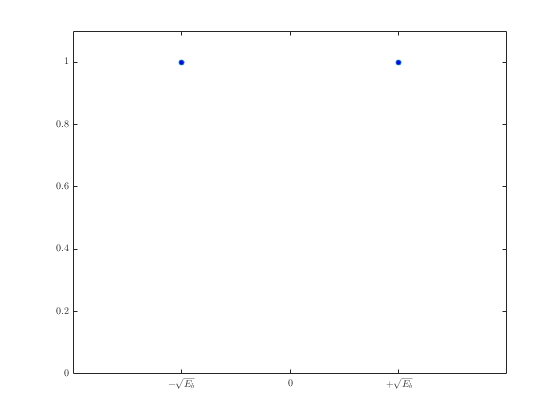
Прежде всего необходимо описать физику процесса. Схема процесса показана ниже:
- Изначальное сообщение кодируется в аналоговый сигнал. “1” кодируется в (+sqrt{E_b}), “0” кодируется в (-sqrt{E_b}). Почему именно как корень из (E_b)? Не знаю. Это единственное место, где я не разобрался.
- После этого сигнал складывается с аддитивным белым гауссовским шумом.
- Далее сигнал демодулируется.
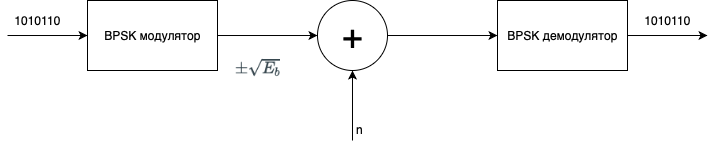
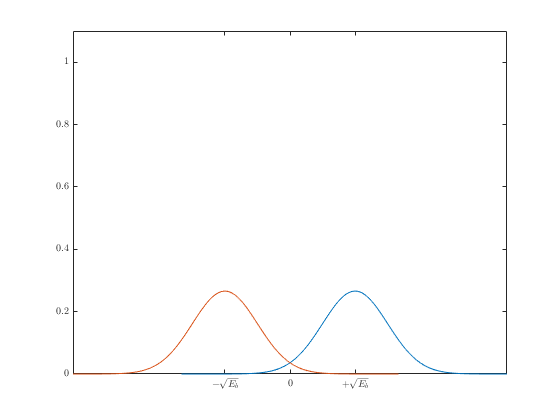
Модулированный BPSK сигнал выглядит следующим образом:
Красными точками обозначается сигнал без шума. Синими — сигнал с добавлением белого гауссовского шума. Как демодулируется этот сигнал? Все точки, которые больше “0” становятся “1”, а те, что меньше “0” становятся “0”. На рисунке выше все синие точки достаточно далеко от “0”, поэтому информацию можно однозначно восстановить. Но что если шум будет сильнее?
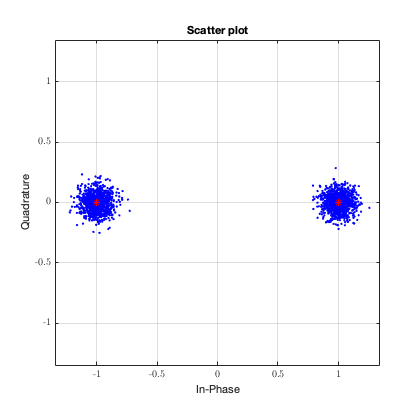
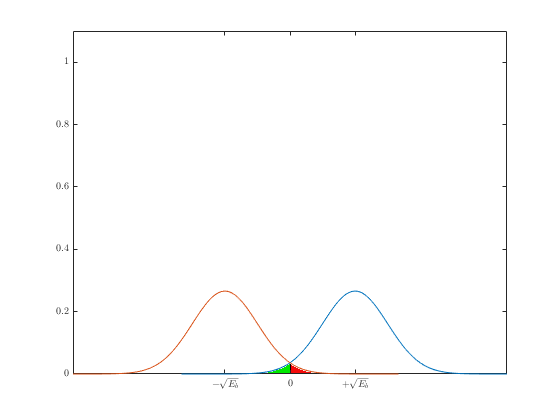
Тут уже не всё так однозначно. Видно, что некоторые точки закодированные как “1” на самом деле оказались меньше “0”. И если бы я попытался их демодулировать, то получил бы неправильную информацию.
Решение
Теперь, когда стало понятно влияние шума на результат демодуляции, можно переходить к графику зависимости вероятности от энергии сигнала. Этот график поможет посчитать вероятность ошибок для различных входных значений. Для начала возьмём сигнал без шума. Вероятность получения “0” или “1” всегда 1.
Частота получения ошибочных битов (Bit error rate) будет 0. Т.е. 0 ошибочных битов на бесконечное количество принятых. В случае наличия гауссовского шума, вероятность получения определяется гауссовской функцией вероятности:
Гауссовский шум определяется следующей формулой:
$$
p(x) = dfrac{1}{sqrt{2pisigma^2}}e^dfrac{-(x-mu)^2}{2sigma^2}
$$
Где:
- (mu=0),
- (sigma^2=N_0/2)
При передаче “1” (mu=+sqrt{E_b}), при “0” (mu=-sqrt{E_b}). Подставляя это в формулу:
$$
begin{align}
P(x|s_0)=dfrac{1}{sqrt{pi N_0}}e^dfrac{-(x+sqrt{E_b})^2}{N_0} newline
P(x|s_1)=dfrac{1}{sqrt{pi N_0}}e^dfrac{-(x-sqrt{E_b})^2}{N_0}
end{align}
$$
Теперь самое интересное.
На этом рисунке показаны области возникновения ошибки. Зелёная область — это место, где возникает ошибка при передаче “1”, красная — при передаче “0”. Общую вероятность ошибки можно записать с помощью формулы полной вероятности:
$$
P(error)=dfrac{1}{2}P(error|s_0) + dfrac{1}{2}P(error|s_1)
$$
После этого необходимо найти каждую из вероятностей:
$$
begin{align}
P(error|s_0) = int_{0}^{infty}P(x|s_0)dx = dfrac{1}{sqrt{pi N_0}}int_{0}^{infty}e^dfrac{-(x+sqrt{E_b})^2}{N_0}dx newline
P(error|s_1) = int_{-infty}^{0}P(x|s_1)dx = dfrac{1}{sqrt{pi N_0}}int_{-infty}^{0}e^dfrac{-(x-sqrt{E_b})^2}{N_0}dx
end{align}
$$
Обычно вероятность ошибки записывают с помощью функции ошибок:
$$
erfc(x)=dfrac{2}{sqrtpi}int_{0}^{x}e^{-t^2}dt
$$
Для этого необходимо сделать следующее:
$$
z=dfrac{y+sqrt{E_b}}{sqrt{N_0}} => zsqrt{N_0} = y + sqrt{E_b}
$$
Заменить пределы интегрирования:
$$
begin{align}
y=0 => z = dfrac{sqrt{E_b}}{sqrt{N_0}} newline
y=infty => z = infty
end{align}
$$
Получившаяся ошибка записывается как:
$$
begin{align}
P(error|s_0)=dfrac{1}{sqrt{pi N_0}}int_limits{sqrt{dfrac{E_b}{N_0}}}^{infty}e^{-z^2}sqrt{N_0}dz
=dfrac{1}{sqrt{pi}}int_limits{sqrt{dfrac{E_b}{N_0}}}^{infty}e^{-z^2}dz
=dfrac{1}{2}erfc(sqrt{dfrac{E_b}{N_0}})
end{align}
$$
Аналогично можно найти ошибку при передаче “1”:
$$
begin{align}
P(error|s_1)=1-P(s_1)=1-dfrac{1}{2}erfc(-sqrt{dfrac{E_b}{N_0}})
end{align}
$$
Можно воспользоваться свойством функции ошибок:
$$
begin{align}
erfc(-x)=2-erfc(x) => P(error|s_1) = dfrac{1}{2}erfc(sqrt{dfrac{E_b}{N_0}})
end{align}
$$
Если подставить в формулу полной вероятности:
$$
P(error)=dfrac{1}{2}(dfrac{1}{2}erfc(sqrt{dfrac{E_b}{N_0}})) + dfrac{1}{2}(dfrac{1}{2}erfc(sqrt{dfrac{E_b}{N_0}}))=dfrac{1}{2}erfc(sqrt{dfrac{E_b}{N_0}})
$$
Ответ
Получившийся график:
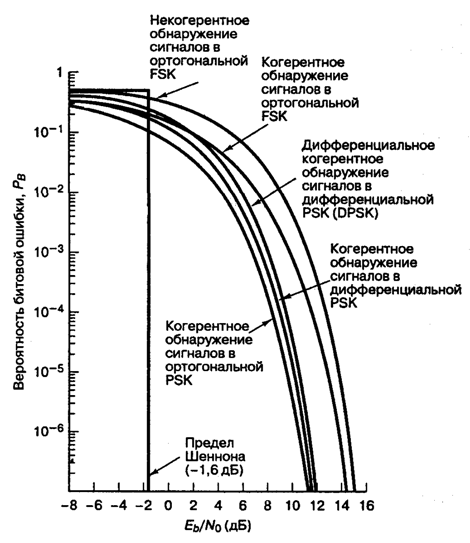
4.7.1. Вероятность появления ошибочного бита при когерентном обнаружении сигнала BPSK
4.7.2. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в дифференциальной модуляции BPSK
4.7.3. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в бинарной ортогональной модуляции FSK
4.7.4. Вероятность появления ошибочного бита при некогерентном обнаружении сигнала в бинарной ортогональной модуляции FSK
4.7.5. Вероятность появления ошибочного бита для бинарной модуляции DPSK
4.7.6. Вероятность ошибки для различных модуляций
4.7.1. Вероятность появления ошибочного бита при когерентном обнаружении сигнала BPSK
Важной мерой производительности, используемой для сравнения цифровых схем модуляции, является вероятность ошибки, РЕ Для коррелятора или согласованного фильтра вычисление РЕ можно представить геометрически (см. рис. 4.6). Расчет РЕ включает нахождение вероятности того, что при данном векторе переданного сигнала, скажем si вектор шума n выведет сигнал из области 1. Вероятность принятия детектором неверного решения называется вероятностью символьной ошибки, рE. Несмотря на то что решения принимаются на символьном уровне, производительность системы часто удобнее задавать через вероятность битовой ошибки (Ps). Связь РВ и РЕ рассмотрена в разделе 4.9.3 для ортогональной передачи сигналов и в разделе 4.9.4 для многофазной передачи сигналов.
Для удобства изложения в данном разделе мы ограничимся когерентным обнаружением сигналов BPSK. В этом случае вероятность символьной ошибки — это то же самое, что и вероятность битовой ошибки. Предположим, что сигналы равновероятны. Допустим также, что при передаче сигнала принятый сигнал r(t) равен
, где n(t) — процесс AWGN; кроме того, мы пренебрегаем ухудшением качества вследствие введенной каналом или схемой межсимвольной интерференции. Как показывалось в разделе 4.4.1, антиподные сигналы
и
можно описать в одномерном сигнальном пространстве, где
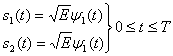
Детектор выбирает с наибольшим выходом коррелятора
; или, в нашем случае антиподных сигналов с равными энергиями, детектор, используя формулу (4.20), принимает решение следующего вида.
(4.74)
Как видно из рис. 4.9, возможны ошибки двух типов: шум так искажает переданный сигнал , что измерения в детекторе дают отрицательную величину z(T), и детектор выбирает гипотезу H2, что был послан сигнал s2(t). Возможна также обратная ситуация: шум искажает переданный сигнал
, измерения в детекторе дают положительную величину z(T), и детектор выбирает гипотезу Н1, соответствующую предположению о передаче сигнала
.
В разделе 3.2.1.1 была выведена формула (3.42), описывающая вероятность битовой ошибки РB для детектора, работающего по принципу минимальной вероятности ошибки.
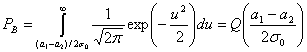
Здесь σ0 — среднеквадратическое отклонение шума вне коррелятора. Функция Q(x), называемая гауссовым интегралом ошибок, определяется следующим образом.
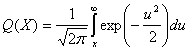
Эта функция подробно описывается в разделах 3.2 и Б.3.2.
Для передачи антиподных сигналов с равными энергиями, таких как сигналы в формате BPSK, приведенные в выражении (4.74), на выход приемника поступают следующие компоненты: , при переданном сигнале
, и
, при переданном сигнале s2(t), где Еь — энергия сигнала, приходящаяся на двоичный символ. Для процесса AWGN дисперсию шума
вне коррелятора можно заменить N0/2 (см. приложение В), так что формулу (4.76) можно переписать следующим образом.
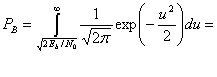
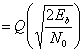
Данный результат для полосовой передачи антиподных сигналов BPSK совпадает с полученными ранее формулами для обнаружения антиподных сигналов с использованием согласованного фильтра (формула (3.70)) и обнаружения узкополосных антиподных сигналов с применением согласованного фильтра (формула (3.76)). Это является примером описанной ранее теоремы эквивалентности. Для линейных систем теорема эквивалентности утверждает, что на математическое описание процесса обнаружения не влияет сдвиг частоты. Как следствие, использование согласованных фильтров или корреляторов для обнаружения полосовых сигналов (рассмотренное в данной главе) дает те же соотношения, что были выведены ранее для сопоставимых узкополосных сигналов.
4.7.2. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в дифференциальной модуляции BPSK
Сигналы в канале иногда инвертируются; например, при использовании когерентного опорного сигнала, генерируемого контуром ФАПЧ, фаза может быть неоднозначной. Если фаза несущей была инвертирована при использовании схемы DPSK, как это скажется на сообщении? Поскольку информация сообщения кодируется подобием или отличием соседних символов, единственным следствием может быть ошибка в бите, который инвертируется, или в бите, непосредственно следующим за инвертированным. Точность определения подобия или отличия символов не меняется при инвертировании несущей. Иногда сообщения (и кодирующие их сигналы) дифференциально кодируются и когерентно обнаруживаются, чтобы просто избежать неопределенности в определении фазы.
Вероятность появления ошибочного бита при когерентном обнаружении сигналов в дифференциальной модуляции PSK (DPSK) дается выражением [5].
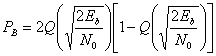
Это соотношение изображено на рис. 4.25. Отметим, что существует незначительное ухудшение достоверности обнаружения по сравнению с когерентным обнаружением сигналов в модуляции PSK. Это вызвано дифференциальным кодированием, поскольку любая отдельная ошибка обнаружения обычно приводит к принятию двух ошибочных решений. Подробно вероятность ошибки при использовании наиболее популярной схемы — когерентного обнаружения сигналов в модуляции DPSK — рассмотрена в разделе 4.7.5.
Рис. 4.25. Вероятность появления ошибочного бита для бинарных систем нескольких типов
4.7.3. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в бинарной ортогональной модуляции FSK
Формулы (4.78) и (4.79) описывают вероятность появления ошибочного бита для когерентного обнаружения антиподных сигналов. Более общую трактовку для когерентного обнаружения бинарных сигналов (не ограничивающихся антиподными сигналами) дает следующее выражение для РВ [6].
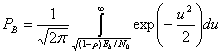
Из формулы (3.64,б) — временной коэффициент взаимной корреляций между
и
, где θ — угол между векторами сигналов
и s2 (см. рис. 4.6). Для антиподных сигналов, таких как сигналы BPSK, θ = π, поэтому ρ = -1.
Для ортогональных сигналов, таких как сигналы бинарной FSK (BFSK), θ = π/2, поскольку векторы и s2 перпендикулярны; следовательно, ρ = 0, что можно доказать с помощью формулы (3.64,а), поэтому выражение (4.81) можно переписать следующим образом.
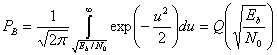
Здесь Q(x) — дополнительная функция ошибок, подробно описанная в разделах 3.2 и Б.3.2. Зависимость (4.82) для когерентного обнаружения ортогональных сигналов BFSK, показанная на рис. 4.25, аналогична зависимости, полученной для обнаружения ортогональных сигналов с помощью согласованного фильтра (формула (3.71)) и узкополосных ортогональных сигналов (униполярных импульсов) с использованием согласованного фильтра (формула (3.73)). В данной книге мы не рассматриваем амплитудную манипуляцию ООК (on-off keying), но соотношение (4.82 применимо к обнаружению с помощью согласованного фильтра сигналов ООК, так же как и к когерентному обнаружению любых ортогональных сигналов.
Справедливость соотношения (4.82) подтверждает и то, что разность энергий между ортогональными векторами сигналов и s2 с амплитудой
, как показано на рис. 3.10, б, равна квадрату расстояния между концами ортогональных векторов Ed = 2Eb. Подстановка этого результата в формулу (3.63) также дает формулу (4.82). Сравнивая формулы (4.82) и (4.79), видим, что, по сравнению со схемой BPSK, схема BFSK требует на 3 дБ большего отношения E/N0 для обеспечения аналогичной достоверности передачи. Этот результат не должен быть неожиданным, поскольку при данной мощности сигнала квадрат расстояния между ортогональными векторами вдвое (на 3 дБ) больше квадрата расстояния между антиподными векторами.
4.7.4. Вероятность появления ошибочного бита при некогерентном обнаружении сигнала в бинарной ортогональной модуляции FSK
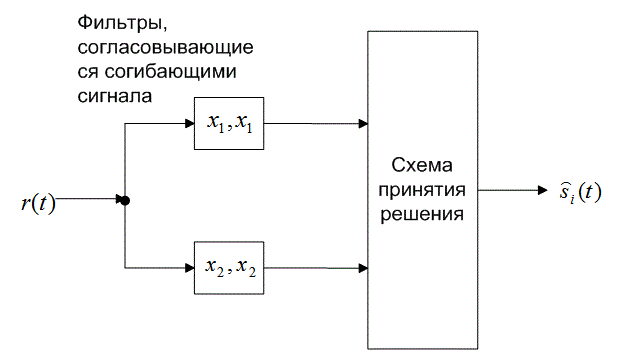
Рассмотрим бинарное ортогональное множество равновероятных сигналов FSK , определенное формулой (4.8).
Фаза φ неизвестна и предполагается постоянной. Детектор описывается М = 2 каналами, состоящими, как показано на рис. 4.19, из полосовых фильтров и детекторов огибающей. На вход детектора поступает принятый сигнал r(t) = si(t) + n(t), где n(i) — гауссов шум с двусторонней спектральной плотностью мощности No/2. Предположим, что и
достаточно разнесены по частоте, чтобы их перекрытием можно было пренебречь. Вычисление вероятности появления ошибочного бита для равновероятных сигналов
и
начнем, как и в случае узкополосной передачи, с уравнения (3.38).
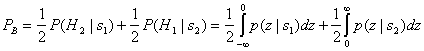
Для бинарного случая тестовая статистика z(T) определена как . Предположим, что полоса фильтра Wf равна 1/T, так что огибающая сигнала FSK (приблизительно) сохраняется на выходе фильтра. При отсутствии шума в приемнике значение z(T) равно
при передаче s1(t) и —
— при передаче s2(t). Вследствие такой симметрии оптимальный порог γ0=0. Плотность вероятности
подобна плотности вероятности
.
(4.84)
Таким образом, можем записать
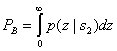
или
(4.86)
где z1 и z2 обозначают выходы z1(T) и z2(T) детекторов огибающей, показанных на рис.4.19. При передаче тона , т.е. когда r(t) = s2(t) + n(t), выход z1(T) состоит исключительно из случайной переменной гауссового шума; он не содержит сигнального компонента. Распределение Гаусса в нелинейном детекторе огибающей дает распределение Релея на выходе [6], так что
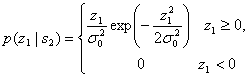
где — шум на выходе фильтра. С другой стороны, z2(T) имеет распределение Раиса, поскольку на вход нижнего детектора огибающей подается синусоида плюс шум [6]. Плотность вероятности p(z2s2) записывается как
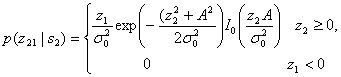
где и, как и ранее,
— шум на выходе фильтра. Функция 10(х), известная как модифицированная функция Бесселя первого рода нулевого порядка [7], определяется следующим образом.
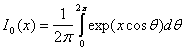
Ошибка при передаче s2(t) происходит, если выборка огибающей z1(T), полученная из верхнего канала (по которому проходит шум), больше выборки огибающей z2(T), полученной из нижнего канала (по которому проходит сигнал и шум). Таким образом, вероятность этой ошибки можно получить, проинтегрировав до бесконечности с последующим усреднением результата по всем возможным z2.
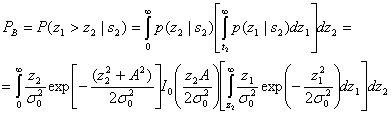
Здесь , внутренний интеграл — условная вероятность ошибки, при фиксированном значении z2, если был передан сигнал s2(1), а внешний интеграл усредняет условную вероятность по всем возможным значениям z2. Данный интеграл можно вычислить аналитически [8], и его значение равно следующему.
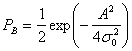
С помощью формулы (1.19) шум на выходе фильтра можно выразить как
(4.93)
где a Wf — ширина полосы фильтра. Таким образом, формула (4.92) приобретает следующий вид.
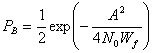
Выражение (4.94) показывает, что вероятность ошибки зависит от ширины полосы полосового фильтра и РB уменьшается при снижении Wf. Результат справедлив только при пренебрежении межсимвольной интерференцией (intersymbol interference — ISI). Минимальная разрешенная Wf (т.е. не дающая межсимвольной интерференции) получается из уравнения (3.81) при коэффициенте сглаживания г = 0. Следовательно, Wf= R бит/с =1/T, и выражение (4.94) можно переписать следующим образом.
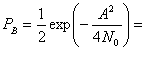
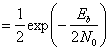
Здесь Еь= (1/2)А2Т — энергия одного бита. Если сравнить вероятность ошибки схем некогерентной и когерентной FSK (см. рис. 4.25), можно заметить, что при равных РB некогерентная FSK требует приблизительно на 1 дБ большего отношения Eb/N0, чем когерентная FSK (для РB < 10-4). При этом некогерентный приемник легче реализуется, поскольку не требуется генерировать когерентные опорные сигналы. По этой причине практически все приемники FSK используют некогерентное обнаружение. В следующем разделе будет показано, что при сравнении когерентной ортогональной схемы FSK с нёкогерентной схемой DPSK имеет место та же разница в 3 дБ, что и при сравнении когерентной ортогональной FSK и когерентной PSK. Как указывалось ранее, в данной книге не рассматривается амплитудная манипуляция ООК (on-off keying). Все же отметим, что вероятность появления ошибочного бита РB, выраженная в формуле (4.96), идентична РB для некогерентного обнаружения сигналов ООК.
4.7.5. Вероятность появления ошибочного бита для бинарной модуляции DPSK
Определим набор сигналов BPSK следующим образом.
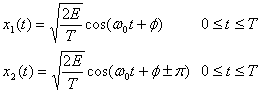
Особенностью схемы DPSK является отсутствие в сигнальном пространстве четко определенных областей решений. В данном случае решение основывается на разности фаз между принятыми сигналами. Таким образом, при передаче сигналов DPSK каждый бит в действительности передается парой двоичных сигналов.
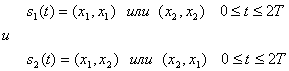
Здесь обозначает сигнал
, за которым следует сигнал
. Первые Т секунд каждого сигнала — это в действительности последние Т секунд предыдущего. Отметим, что оба сигнала s1(t) и s2(t) могут принимать любую из возможных форм и что
и
— это антиподные сигналы. Таким образом, корреляцию между
и s2(t) для любой комбинации сигналов можно записать следующим образом.
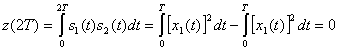
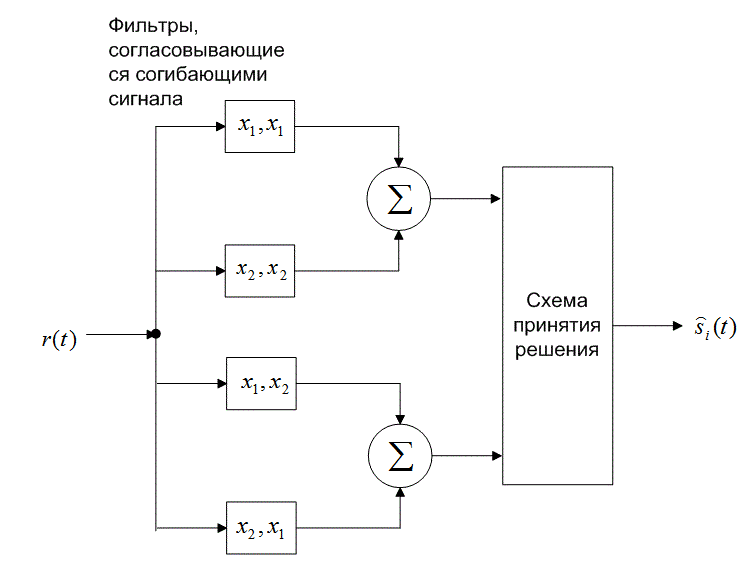
Следовательно, каждую пару сигналов DPSK можно представить как ортогональный сигнал длительностью 2Т секунд. Обнаружение может соответствовать некогерентному обнаружению огибающей с помощью четырех каналов, согласованных с каждым возможным выходом огибающей, как показано на рис. 4.26. Поскольку два детектора огибающей, представляющих каждый символ, обратны друг другу, выборки их огибающих будут совпадать. Значит, мы можем реализовать детектор как один канал для , согласовывающегося с
или
, и один канал для
, согласовывающегося с
или
, как показано на рис. 4.26. Следовательно, детектор DPSK сокращается до стандартного двухканального некогерентного детектора. В действительности фильтр может согласовываться с разностным сигналом; так что необходимым является всего один канал. На рис. 4.26 показаны фильтры, которые согласовываются с огибающими сигнала (в течение двух периодов передачи символа). Что это означает, если вспомнить, что DPSK — это схема передачи сигналов с постоянной огибающей? Это означает, что нам требуется реализовать детектор энергии, подобный квадратурному приемнику на рис. 4.18, где каждый сигнал в течение периода
представляется синфазным и квадратурным опорными сигналами.
синфазный опорный сигнал квадратурный опорный сигнал
синфазный опорный сигнал
квадратурный опорный сигнал
Поскольку пары сигналов DPSK ортогональны, вероятность ошибки при подобном некогерентном обнаружении дается выражением (4.96). Впрочем, поскольку сигналы DPSK длятся 2Т секунд, энергия сигналов , определенных в формуле (4.98), равна удвоенной энергии сигнала, определенного в течение одного периода передачи символа.
а)
б)
Рис. 4.26. Обнаружение в схеме DPSK: а) четырехканальное дифференциально-когерентное обнаружение сигналов в бинарной модуляции DPSK; б) эквивалентный двухканальный детектор сигналов в бинарной модуляции DPSK
Таким образом, РВможно записать в следующем виде.
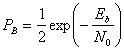
Зависимость (4.100), изображенная на рис. 4.25, представляет собой дифференциальное когерентное обнаружение сигналов в дифференциальной модуляции PSK, или просто DPSK. Выражение справедливо для оптимального детектора DPSK (рис. 4.17, в). Для детектора, показанного на рис. 4.17, б, вероятность ошибки будет несколько выше приведенной в выражении (4.100) [3]. Если сравнить вероятность ошибки, приведенную в формуле (4.100), с вероятностью ошибки когерентной схемы PSK (см. рис. 4.25), видно, что при равных РB схема DPSK требует приблизительно на 1 дБ большего отношения E^N0, чем схема BPSK (для ). Систему DPSK реализовать легче, чем систему PSK, поскольку приемник DPSK не требует фазовой синхронизации. По этой причине иногда предпочтительнее использовать менее эффективную схему DPSK, чем более сложную схему PSK.
4.7.6. Вероятность ошибки для различных модуляций
В табл. 4.1 и на рис. 4.25 приведены аналитические выражения и графики РB для наиболее распространенных схем модуляции, описанных выше. Для РB = 10-4 можно видеть, что разница между лучшей (когерентной PSK) и худшей (некогерентной ортогональной FSK) из рассмотренных схем равна приблизительно 4 дБ. В некоторых случаях 4 дБ — это небольшая цена за простоту реализации, увеличивающуюся от когерентной схемы PSK до некогерентной FSK (рис. 4.25); впрочем, в других случаях ценным является даже выигрыш в 1 дБ. Помимо сложности реализации и вероятности РB существуют и другие факторы, влияющие на выбор модуляции; например, в некоторых случаях (в каналах со случайным затуханием) желательными являются некогерентные системы, поскольку иногда когерентные опорные сигналы затруднительно определять и использовать. В военных и космических приложениях весьма желательны сигналы, которые могут противостоять значительному ухудшению качества, сохраняя возможность обнаружения.
Таблица 4.1. Вероятность ошибки для различных бинарных модуляций
|
Модуляция |
PB |
|
PSK (когерентное обнаружение) |
|
|
DPSK (дифференциальное когерентное обнаружение) |
|
|
Ортогональная FSK (когерентное обнаружение) |
|
|
Ортогональная FSK (некогерентное обнаружение) |
|
Pв
– вероятность ошибки зависит от
соотношения «сигнал/шум».
Pв=f(ОСШ)
Д
бинарного случая
ОСШ=Eb/No
Eb
– энергия
бита
No
– спектральная
плотность мощности шума
ОСШ=Eb/No=(PS/PN)*(ΔF/C)
PS
– мощность
сигнала
No
– мощность
шума
PS/PN
= 2С/ΔF-1
C=log2(PS/PN+1)
– формула Шеннона.
Для m-мерной
ES=Eblog2M
M-
разрядность системы (сколько уровней
может принимать единичный импульс). ES
– энергия
символа.
В большинстве
формул для определения вероятности
используется функция Крампа
18 Кодирование
Суть
линейного кодирования заключается в
преобразовании последовательности
передаваемых импульсов с целью
уменьшения мощности передатчика и
сужения требуемой полосы частот.
1)
Потенциальный код без возращения к 0
«+»
– простота реализации; хорошая
распознаваемость ошибок (благодоря
наличию 2-х однозначно отличающихся
потенциалов); сравнительно узкий спектр
«-»
– метод не обладает свойством
самосинхронизации; при высоких скоростях
обмена данными или длинных последовательностей
1 или 0 не большое рассогласование
тактовых частот может привести к
некоторому считыванию битов; наличие
низкочастотной составляющей, кот.
приближается к постоянному сигналу
при передачи длинных последовательностей
нулей или единиц.
2)
Биполярное кодирование. бипол-й код
явл. модификацией потенциального с
альтернат-й инверсией. В этом методе
использ-ся 3 уровня потенциала: «0» лог
кодируется 0, «1 лог» код-ся либо
положительным потенц-ом либо отрицат-м
в зависимости от предыдущего значения
1, т.е. каждый послед. потенциал 1
противополож. предыдущему. Этот код
частично решает проблему постоян-й
составл-ей. Длинные последов-ти нулей
характ-ся наличием постоян-й составляющей.
При равномерном потоке 0 и 1 спектр
сигнала более узкий по сравнению с
потенц-м кодом.
3)
Потенциальный код с инверсией используется
2 уровня сигнала при передаче нуля
перед-ся потенциал установ-й в педыдущем
такте. При передаче 1 сигнал инверт-ся
на противоположный. Этот код удобен в
случае если наличие 3-го уровня сигнала
нежел-но. Например в оптич-х системах.
Для улучшения потенц-х кодов испол-ся
2 метода: 1. Основан на добавл-нии в исход-й
код исбыточ-х битов, содерж-х лог. «1». В
этом случае длинные послед-ти 0 прерываются,
исчезает постоя-я составляющ-я, сужает-ся
спектр, однако снижается полезная
пропуск-я способ-ть. 2-й метод основан
на предварительном перемешивании
битового потока, след-но вероят-ть
появл-я 0 и 1 стан-ся практич-ки одинаковой.
4) Биполярный
импульсный код. Данные представлены
фронтом сигнала. «1» — импульс одной
полярности; «0» — другой. «+» — хорошая
самосинхронизирующая способность; «-»
– широкий спектр; наличие постоянной
составляющей при передаче длительной
последовательности импульсов 0 и 1.
19 Сравнение кодов, используемых в каналообразующих устройствах
Основными кодами,
используемыми в коу, являются: NRZ,
AMI,
NRZI,
биполярный импульсный, манчестерский,
2B1Q.
Код NRZ
обладает узким спектром, хорошей
распознаваемостью ошибок и простотой
реализации.
AMI-код
обладает хорошими синхронизирующими
свойствами при передаче серий единиц
и сравнительно прост в реализации.
Недостатком кода является ограничение
на плотность нулей в потоке данных,
поскольку длинные последовательности
нулей ведут к потере синхронизации.
Код NRZI
удобен в тех случаях, когда наличие
третьего уровня сигнала весьма
нежелательно, например в оптических
кабелях, где устройство распознаются
только два сигнала – свет и темнота.
Биполярный
импульсный код обладает отличными
самосинхронизирующими свойствами, но
постоянная составляющая, может
присутствовать, например, при передаче
длинной последовательности единиц или
нулей. Кроме того, спектр у него шире,
чем у потенциальных кодов.
Полоса пропускания
манчестерского
кода уже,
чем у биполярного импульсного. У него
также нет постоянной составляющей, а
основная гармоника в худшем случае (при
передаче последовательности единиц
или нулей) имеет частоту N Гц, а в лучшем
(при передаче чередующихся единиц и
нулей) она равна N/2 Гц, как и у кодов AMI
или NRZ. В среднем ширина полосы
манчестерского кода в полтора раза уже,
чем у биполярного импульсного кода, а
основная гармоника колеблется вблизи
значения 3N/4. Манчестерский код имеет
еще одно преимущество перед биполярным
импульсным кодом. В последнем для
передачи данных используются три уровня
сигнала, а в манчестерском — два.
Сигнальная скорость
у кода 2B1Q
в два раза ниже, чем у кодов NRZ
и AMI,
а спектр сигнала в два раза уже.
Следовательно с помощью 2B1Q-кода
можно по одной и той же линии передавать
данные в два раза быстрее, однако для
его реализации мощность передатчика
должна быть выше, чтобы четыре уровня
четко различались приемником на фоне
помех.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тип кодирования данных
Фазовая манипуляция (PSK ) — это цифровая модуляция процесс, который передает данные путем изменения (модуляции) фазы постоянного частоты эталонного сигнала ( несущая ). Модуляция осуществляется путем изменения входных сигналов синус и косинус в точное время. Он широко используется для беспроводных локальных сетей, RFID и Bluetooth связи.
Любая схема цифровой модуляции использует конечное количество различных сигналов для представления цифровых данных. PSK использует конечное количество фаз, каждой из которых назначен уникальный шаблон из двоичных цифр. Обычно каждая фаза кодирует равное количество битов. Каждый набор битов образует символ , который представлен конкретной фазой. Демодулятор , который разработан специально для набора символов, используемого модулятором, определяет фазу принятого сигнала и отображает ее обратно в символ, который он представляет, таким образом восстанавливая исходные данные. Для этого приемник должен иметь возможность сравнивать фазу принятого сигнала с опорным сигналом — такая система называется когерентной (и упоминается как CPSK).
CPSK требует сложного демодулятора, поскольку он должен извлекать опорную волну из принятого сигнала и отслеживать ее, чтобы сравнивать каждую выборку. В качестве альтернативы, фазовый сдвиг каждого отправленного символа можно измерить относительно фазы предыдущего отправленного символа. Поскольку символы кодируются с разностью фаз между последовательными выборками, это называется дифференциальной фазовой манипуляцией (DPSK) . DPSK может быть значительно проще в реализации, чем обычный PSK, поскольку это «некогерентная» схема, то есть демодулятору не нужно отслеживать опорную волну. Компромисс в том, что он имеет больше ошибок демодуляции.
Содержание
- 1 Введение
- 1.1 Определения
- 2 Приложения
- 3 Двоичная фазовая манипуляция (BPSK)
- 3.1 Реализация
- 3.2 Частота битовых ошибок
- 4 Квадратурная фаза- Shift-манипуляция (QPSK)
- 4.1 Реализация
- 4.2 Вероятность ошибки
- 4.3 Варианты
- 4.3.1 Смещение QPSK (OQPSK)
- 4.3.2 SOQPSK
- 4.3.3 π / 4- QPSK
- 4.3.4 DPQPSK
- 5 PSK высшего порядка
- 5.1 Частота битовых ошибок
- 5.2 Спектральная эффективность
- 6 Дифференциальная фазовая манипуляция (DPSK)
- 6.1 Дифференциальное кодирование
- 6.2 Демодуляция
- 6.3 Пример: дифференциально-кодированная BPSK
- 7 Взаимная информация с аддитивным белым гауссовским шумом
- 8 См. Также
- 9 Примечания
- 10 Ссылки
Введение
Есть три основных класса методов цифровой модуляции, используемых для передачи представленных в цифровом виде данных:
Все передают данные, изменяя какой-либо аспект основного знака al, несущая (обычно синусоида ) в ответ на сигнал данных. В случае PSK фаза изменяется для представления сигнала данных. Существует два основных способа использования фазы сигнала таким образом:
- путем рассмотрения самой фазы как передачи информации, и в этом случае демодулятор должен иметь опорный сигнал. сигнал для сравнения фазы принятого сигнала; или
- При просмотре изменения в фазе, как транспортирующая информация -. дифференциального схема, некоторые из которых не нужен опорный носителя (в определенную степень)
Удобный способ представления схем PSK — это диаграмма созвездия . Здесь показаны точки на комплексной плоскости , где в данном контексте оси действительная и мнимая называются синфазной и квадратурной осями соответственно из-за их Разделение на 90 °. Такое представление на перпендикулярных осях легко реализуется. Амплитуда каждой точки вдоль синфазной оси используется для модуляции косинусной (или синусоидальной) волны, а амплитуда вдоль квадратурной оси — для модуляции синусоидальной (или косинусной) волны. По соглашению синфазная модуляция модулирует косинус, а квадратурная модуляция синуса.
В PSK выбранные точки созвездия обычно располагаются с равномерным угловым интервалом вокруг окружности. Это обеспечивает максимальное разделение фаз между соседними точками и, следовательно, лучшую защиту от повреждений. Они расположены по кругу, поэтому все они могут передаваться с одинаковой энергией. Таким образом, модули комплексных чисел, которые они представляют, будут такими же, как и амплитуды, необходимые для косинусной и синусоидальной волн. Двумя распространенными примерами являются «двоичная фазовая манипуляция» (BPSK), которая использует две фазы, и «квадратурная фазовая манипуляция» (QPSK), которая использует четыре фазы, хотя любое количество фаз могут быть использованы. Поскольку данные, которые должны быть переданы, обычно являются двоичными, схема PSK обычно разрабатывается с количеством точек совокупности, равным степени двух.
Определения
Для математического определения частоты ошибок потребуются некоторые определения:
Q (x) { displaystyle Q (x)}

- Q (x) = 1 2 π ∫ x ∞ e — 1 2 t 2 dt = 1 2 erfc (x 2), x ≥ 0 { displaystyle Q (x) = { frac {1} { sqrt {2 pi}}} int _ {x} ^ { infty} e ^ {- { frac {1} {2}} t ^ { 2}} , dt = { frac {1} {2}} operatorname {erfc} left ({ frac {x} { sqrt {2}}} right), x geq 0}
.
Приведенные здесь коэффициенты ошибок соответствуют аддитивному белому гауссовскому шуму (AWGN). Эти коэффициенты ошибок ниже, чем вычисленные в каналах с замираниями, следовательно, они являются хорошим теоретическим эталоном для сравнения.
Приложения
Благодаря простоте PSK, особенно по сравнению с его конкурентом квадратурной амплитудной модуляцией, он широко используется в существующих технологиях.
Стандарт беспроводной локальной сети, IEEE 802.11b-1999, использует различные PSK в зависимости от требуемой скорости передачи данных. При базовой скорости 1 Мбит / с он использует DBPSK (дифференциальный BPSK). Для обеспечения расширенной скорости 2 Мбит / с используется DQPSK. При достижении 5,5 Мбит / с и полной скорости 11 Мбит / с используется QPSK, но он должен сочетаться с вводом дополнительного кода. Стандарт высокоскоростной беспроводной локальной сети, IEEE 802.11g-2003, имеет восемь скоростей передачи данных: 6, 9, 12, 18, 24, 36, 48 и 54 Мбит / с. В режимах 6 и 9 Мбит / с используется модуляция OFDM, где каждая поднесущая модулируется BPSK. В режимах 12 и 18 Мбит / с используется OFDM с QPSK. Четыре самых быстрых режима используют OFDM с формами квадратурной амплитудной модуляции.
Из-за своей простоты BPSK подходит для недорогих пассивных передатчиков и используется в стандартах RFID, таких как ISO / IEC 14443, который был принят для биометрических паспортов, кредитных карт, таких как American Express, ExpressPay, и многих других приложений.
Bluetooth 2 использует π / 4 { displaystyle pi / 4}
И QPSK, и 8PSK широко используются в спутниковом вещании. QPSK по-прежнему широко используется при потоковой передаче спутниковых каналов SD и некоторых каналов HD. Программы высокого разрешения передаются почти исключительно в 8PSK из-за более высоких битрейтов HD-видео и высокой стоимости спутниковой полосы пропускания. Стандарт DVB-S2 требует поддержки как QPSK, так и 8PSK. Наборы микросхем, используемые в новых спутниковых приставках, таких как серия 7000 компании Broadcom, поддерживают 8PSK и обратно совместимы со старым стандартом.
Исторически сложилось так, что модемы с синхронизацией голосового диапазона , например, Bell 201, 208 и 209 и CCITT V.26, V.27, V.29, V.32 и V.34 использовали PSK.
Двоичная фазовая манипуляция (BPSK)

BPSK (также иногда называемый PRK, фазовой манипуляцией или 2PSK) — это простейшая форма фазовой манипуляции (PSK). В нем используются две фазы, разделенные на 180 °, поэтому их также можно назвать 2-PSK. Не имеет особого значения, где именно расположены точки созвездия, и на этом рисунке они показаны на действительной оси в точках 0 ° и 180 °. Следовательно, он обрабатывает самый высокий уровень шума или искажения до того, как демодулятор примет неверное решение. Это делает его самым надежным из всех PSK. Однако он может модулировать только со скоростью 1 бит / символ (как показано на рисунке) и поэтому не подходит для приложений с высокой скоростью передачи данных.
При наличии произвольного фазового сдвига, вносимого каналом связи, демодулятор (см., Например, цикл Костаса ) не может определить, какая точка совокупности который. В результате данные часто дифференциально кодируются перед модуляцией.
BPSK функционально эквивалентен модуляции 2-QAM.
Реализация
Общая форма для BPSK следует уравнению:
- sn (t) = 2 E b T b cos (2 π ft + π (1 — n)), п = 0, 1. { displaystyle s_ {n} (t) = { sqrt { frac {2E_ {b}} {T_ {b}}}} cos (2 pi ft + pi (1-n)), quad n = 0,1.}
Это дает две фазы, 0 и π. В особой форме двоичные данные часто передаются с помощью следующих сигналов:
- s 0 (t) = 2 E b T b cos (2 π ft + π) = — 2 E b T b cos (2 π фут) { displaystyle s_ {0} (t) = { sqrt { frac {2E_ {b}} {T_ {b}}}} cos (2 pi ft + pi) = — { sqrt { frac {2E_ {b}} {T_ {b}}}} cos (2 pi ft)}
для двоичного «0»
- s 1 (t) = 2 E b T b cos (2 π фут) { displaystyle s_ {1} (t) = { sqrt { frac {2E_ {b}} {T_ {b}}}} cos (2 pi ft)}
для двоичной «1»
, где f — частота основной полосы частот.
Следовательно, пространство сигналов может быть представлено единственной базисной функцией
- ϕ (t) = 2 T b cos (2 π ft) { displaystyle phi (t) = { sqrt { frac {2} {T_ {b}}}} cos (2 pi ft)}
где 1 представлено как E b ϕ (t) { displaystyle { sqrt {E_ {b}}} phi (t)}

Это использование этой базовой функции показано в конце следующего раздела на временной диаграмме сигнала. Самый верхний сигнал — это косинусоидальная волна, модулированная BPSK, которую будет производить модулятор BPSK. Битовый поток, который вызывает этот вывод, показан над сигналом (другие части этого рисунка относятся только к QPSK). После модуляции сигнал основной полосы будет перемещен в полосу высоких частот путем умножения cos (2 π fct) { displaystyle cos (2 pi f_ {c} t)}
Коэффициент битовых ошибок
коэффициент битовых ошибок (BER) BPSK при аддитивном белом гауссовском шуме (AWGN) можно рассчитать как:
- P b = Q (2 E b N 0) { displaystyle P_ {b} = Q left ({ sqrt { frac {2E_ {b}} {N_ {0}}}} right)}
или P е = 1 2 erfc (E b N 0) { displaystyle P_ {e} = { frac {1} {2}} operatorname {erfc} left ({ sqrt { frac {E_ {b}}) {N_ {0}}}} right)}
Поскольку на каждый символ приходится только один бит, это также частота ошибок символа.
Квадратурная фазовая манипуляция (QPSK)

Иногда это называется четырехфазным PSK, 4-PSK или 4- QAM. (Хотя основные концепции QPSK и 4-QAM различны, результирующие модулированные радиоволны точно такие же.) QPSK использует четыре точки на диаграмме созвездия, равномерно распределенные по кругу. С четырьмя фазами QPSK может кодировать два бита на символ, показанные на диаграмме с кодированием Грея, чтобы минимизировать коэффициент ошибок по битам (BER) — иногда ошибочно воспринимается как удвоенный BER, чем BPSK.
Математический анализ показывает, что QPSK может использоваться либо для удвоения скорости передачи данных по сравнению с системой BPSK при сохранении той же полосы пропускания сигнала, либо для поддержания скорости передачи данных BPSK. но необходимо сократить вдвое полосу пропускания. В последнем случае BER QPSK в точности совпадает с BER BPSK — и полагать иначе — это обычная путаница при рассмотрении или описании QPSK. Переданная несущая может претерпевать ряд фазовых изменений.
Учитывая, что каналы радиосвязи распределяются такими агентствами, как Федеральная комиссия по связи, что дает предписанную (максимальную) полосу пропускания, преимущество QPSK над BPSK становится очевидным: QPSK передает в два раза большую скорость передачи данных в заданной полосе пропускания по сравнению с BPSK — при том же BER. Плата за техническое обслуживание состоит в том, что передатчики и приемники QPSK сложнее, чем передатчики для BPSK. Однако с современной технологией электроники снижение стоимости очень умеренное.
Как и в случае с BPSK, на принимающей стороне возникают проблемы с фазовой неоднозначностью, и на практике часто используется дифференциально кодированный QPSK.
Реализация
Реализация QPSK является более общей, чем реализация BPSK, а также указывает на реализацию PSK более высокого порядка. Записывая символы на диаграмме созвездия в виде синусоидальных и косинусоидальных волн, используемых для их передачи:
- sn (t) = 2 E s T s cos (2 π fct + (2 n — 1) π 4), n = 1, 2, 3, 4. { displaystyle s_ {n} (t) = { sqrt { frac {2E_ {s}} {T_ {s}}}} cos left (2 pi f_ {c} t + (2n-1) { frac { pi} {4}} right), quad n = 1,2,3,4.}
Это дает четыре фазы π / 4, 3π / 4, 5π / 4 и 7π / 4 по мере необходимости.
Это приводит к двумерному сигнальному пространству с единицами базисных функций
- ϕ 1 (t) = 2 T s cos (2 π fct) ϕ 2 (t) = 2 T s грех (2 π fct) { displaystyle { begin {align} phi _ {1} (t) = { sqrt { frac {2} {T_ {s}}}} cos left (2 pi f_ {c} t right) \ phi _ {2} (t) = { sqrt { frac {2} {T_ {s}}}} sin left (2 pi f_ { c} t right) end {align}}}
Первая базовая функция используется как синфазная составляющая сигнала, а вторая как квадратурная составляющая сигнала.
Следовательно, совокупность сигналов состоит из 4 точек
- пространства сигнала (± E s 2 ± E s 2). { displaystyle { begin {pmatrix} pm { sqrt { frac {E_ {s}} {2}}} pm { sqrt { frac {E_ {s}} {2}}} end {pmatrix}}.}
Коэффициент 1/2 показывает, что общая мощность поровну делится между двумя несущими.
Сравнение этих базовых функций с функциями для BPSK ясно показывает, как QPSK можно рассматривать как два независимых сигнала BPSK. Обратите внимание, что точки пространства сигнала для BPSK не нуждаются в разделении энергии символа (бита) по двум несущим в схеме, показанной на диаграмме созвездия BPSK.
Системы QPSK могут быть реализованы несколькими способами. Ниже показаны основные компоненты конструкции передатчика и приемника.


Вероятность ошибки
Хотя QPSK можно рассматривать как четвертичную модуляцию, его легче рассматривать как две независимо модулированные квадратурные носители. При такой интерпретации четные (или нечетные) биты используются для модуляции синфазной составляющей несущей, в то время как нечетные (или четные) биты используются для модуляции квадратурной составляющей несущей. BPSK используется на обеих несущих, и их можно независимо демодулировать.
В результате вероятность битовой ошибки для QPSK такая же, как для BPSK:
- P b = Q (2 E b N 0) { displaystyle P_ {b} = Q left ({ sqrt { frac {2E_ {b}} {N_ {0}}}} right)}
Однако для достижения той же вероятности битовой ошибки, что и BPSK, QPSK использует вдвое большую мощность (поскольку два бита передаются одновременно).
Коэффициент ошибок символа определяется следующим образом:
- P s = 1 — (1 — P b) 2 = 2 Q (E s N 0) — [Q (E s N 0)] 2. { displaystyle { begin {align} P_ {s} = 1- left (1-P_ {b} right) ^ {2} \ = 2Q left ({ sqrt { frac {E_ { s}} {N_ {0}}}} right) — left [Q left ({ sqrt { frac {E_ {s}} {N_ {0}}}} right) right] ^ { 2}. End {align}}}
Если отношение сигнал / шум высокое (что необходимо для практических систем QPSK), вероятность ошибки символа может быть приблизительно равна:
- P s ≈ 2 Q (E s N 0) = erfc (E s 2 N 0) = erfc (E b N 0) { displaystyle P_ {s} приблизительно 2Q left ({ sqrt { frac { E_ {s}} {N_ {0}}}} right) = operatorname {erfc} left ({ sqrt { frac {E_ {s}} {2N_ {0}}}} right) = operatorname {erfc} left ({ sqrt { frac {E_ {b}} {N_ {0}}}} right)}
Модулированный сигнал показан ниже для короткого сегмента случайных двоичных данных — поток. Две несущие волны представляют собой косинусоидальную и синусоидальную волну, как показывает анализ пространства сигналов выше. Здесь биты с нечетными номерами назначены синфазному компоненту, а биты с четными номерами — квадратурному компоненту (принимая первый бит за номер 1). Общий сигнал — сумма двух компонентов — показан внизу. Скачки по фазе можно увидеть, поскольку PSK изменяет фазу на каждом компоненте в начале каждого битового периода. Самая верхняя форма волны соответствует описанию, данному для BPSK выше.
.
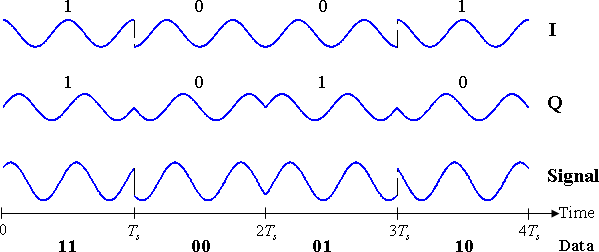
Двоичные данные, которые передаются этим сигналом: 11000110.
- Нечетные биты, выделенные здесь, вносят вклад в синфазную составляющую: 11000110
- Четные биты, выделенные здесь, вносят вклад в квадратурно-фазовую составляющую: 11000110
Варианты
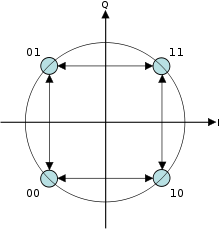
QPSK смещения (OQPSK)
Квадратурная фазовая манипуляция со смещением (OQPSK) — это вариант модуляции с фазовой манипуляцией, использующий четыре различных значения фазы для передачи. Иногда это называют ступенчатой квадратурной фазовой манипуляцией (SQPSK).

Одновременное использование четырех значений фазы (два бита ) для построения символа QPSK может позволить фазе сигнала прыгнуть на столько же как 180 ° за раз. Когда сигнал фильтруется нижними частотами (как это обычно бывает в передатчике), эти фазовые сдвиги приводят к большим колебаниям амплитуды, что является нежелательным качеством в системах связи. При смещении синхронизации нечетных и четных битов на один битовый период или половину периода символа синфазная и квадратурная составляющие никогда не изменятся одновременно. На диаграмме созвездия, показанной справа, можно увидеть, что это ограничит фазовый сдвиг не более чем на 90 ° за раз. Это дает гораздо меньшие колебания амплитуды, чем QPSK без смещения, и иногда это предпочтительнее на практике.
На рисунке справа показана разница в поведении фазы между обычным QPSK и OQPSK. Видно, что на первом графике фаза может измениться сразу на 180 °, а в OQPSK изменения никогда не превышают 90 °.
Модулированный сигнал показан ниже для короткого сегмента случайного потока двоичных данных. Обратите внимание на сдвиг на половину периода символа между двумя составляющими волнами. Внезапные сдвиги фазы происходят примерно в два раза чаще, чем при QPSK (поскольку сигналы больше не изменяются вместе), но они менее серьезны. Другими словами, величина скачков меньше в OQPSK по сравнению с QPSK.

SOQPSK
Безлицензионный сформированный -смещение QPSK (SOQPSK) совместим с Feher- запатентованный QPSK (FQPSK ) в том смысле, что детектор QPSK с интегрированием и сбросом смещения дает одинаковый выходной сигнал независимо от типа используемого передатчика.
Эти модуляции тщательно формируют I и формы волны Q, так что они изменяются очень плавно, и сигнал остается постоянной амплитуды даже во время переходов сигнала. (Вместо мгновенного перехода от одного символа к другому или даже линейного, он плавно перемещается по кругу с постоянной амплитудой от одного символа к другому.) Модуляция SOQPSK может быть представлена как гибрид QPSK и MSK : SOQPSK имеет ту же совокупность сигналов, что и QPSK, однако фаза SOQPSK всегда стационарна.
Стандартное описание SOQPSK-TG включает троичные символы. SOQPSK — одна из наиболее распространенных схем модуляции в применении к спутниковой связи LEO.
π / 4-QPSK

В этом варианте QPSK используются два идентичных созвездия, повернутых на 45 ° (π / 4 { displaystyle pi / 4}

Одно свойство, которым обладает эта схема модуляции, заключается в том, что если модулированный сигнал представлен в комплексной области, переходы между символами никогда не проходят через 0. Другими словами, сигнал не проходит через начало координат. Это снижает динамический диапазон колебаний сигнала, что желательно при разработке сигналов связи.
С другой стороны, π / 4 { displaystyle pi / 4}
Модулированный сигнал показан ниже для короткого сегмента случайного потока двоичных данных. Конструкция такая же, как и для обычного QPSK. Последовательные символы взяты из двух созвездий, показанных на схеме. Таким образом, первый символ (11) взят из «синего» созвездия, а второй символ (0 0) взят из «зеленого» созвездия. Обратите внимание, что величины двух составляющих волн изменяются при переключении между созвездиями, но общая величина сигнала остается постоянной (постоянная огибающая ). Фазовые сдвиги находятся между двумя предыдущими временными диаграммами.

DPQPSK
Квадратурная фазовая манипуляция с двойной поляризацией (DPQPSK) или QPSK с двойной поляризацией — включает поляризационное мультиплексирование двух разных сигналов QPSK, таким образом улучшая спектральную эффективность в 2 раза. Это экономичная альтернатива использованию 16-PSK вместо QPSK для удвоения спектральной эффективности.
PSK высшего порядка
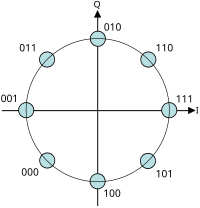
Для построения совокупности PSK можно использовать любое количество фаз, но 8-PSK обычно является развернутой совокупностью PSK высшего порядка. При более чем 8 фазах частота ошибок становится слишком высокой, и доступны более качественные, хотя и более сложные модуляции, такие как квадратурная амплитудная модуляция (QAM). Хотя может использоваться любое количество фаз, тот факт, что совокупность обычно должна иметь дело с двоичными данными, означает, что количество символов обычно является степенью 2, чтобы обеспечить целое число битов на символ.
Коэффициент битовых ошибок
Для общего M-PSK не существует простого выражения для вероятности ошибки символа, если M>4 { displaystyle M>4}
- P s = 1 — ∫ — π / M π / M p θ r (θ r) d θ r, { displaystyle P_ {s} = 1- int _ {- pi / M } ^ { pi / M} p _ { theta _ {r}} left ( theta _ {r} right) d theta _ {r},}
где
- p θ r (θ r) = 1 2 π e — 2 γ s sin 2 θ r ∫ 0 ∞ V e — 1 2 (V — 2 γ s cos θ r) 2 d V, V = r 1 2 + r 2 2, θ р знак равно загар — 1 (р 2 р 1), γ s знак равно Е s N 0 { Displaystyle { begin {align} p _ { theta _ {r}} left ( theta _ {r} right) = { frac {1} {2 pi}} e ^ {- 2 gamma _ {s} sin ^ {2} theta _ {r}} int _ {0} ^ { infty} Ve ^ {- { frac {1} {2}} left (V-2 { sqrt { gamma _ {s}}} cos theta _ {r} right) ^ {2}} , dV, \ V = { sqrt {r_ {1} ^ {2} + r_ {2} ^ {2}}}, \ theta _ {r} = tan ^ {- 1} left ({ frac {r_ {2}} {r_ {1}}} r ight), \ gamma _ {s} = { frac {E_ {s}} {N_ {0}}} end {align}}}
и r 1 ∼ N (E s, 1 2 N 0) { displaystyle r_ {1} sim N left ({ sqrt {E_ {s}}}, { frac {1} {2}} N_ {0} right)}


Это может быть приблизительно для высокого M { displaystyle M}

- P s ≈ 2 Q (2 γ s sin π M). { displaystyle P_ {s} приблизительно 2Q left ({ sqrt {2 gamma _ {s}}} sin { frac { pi} {M}} right).}
Бит- вероятность ошибки для M { displaystyle M}
- P b ≈ 1 k P s. { displaystyle P_ {b} приблизительно { frac {1} {k}} P_ {s}.}
(Использование кодирования Грея позволяет нам приблизить расстояние Ли ошибок как Расстояние Хэмминга ошибок в декодированном потоке битов, которое легче реализовать аппаратно.)
На графике слева сравниваются коэффициенты битовых ошибок BPSK, QPSK (которые являются то же, что и отмечалось выше), 8-PSK и 16-PSK. Видно, что модуляция более высокого порядка демонстрирует более высокие коэффициенты ошибок; однако взамен они обеспечивают более высокую скорость необработанных данных.
Границы частоты ошибок для различных схем цифровой модуляции могут быть вычислены с применением объединения к сигнальной совокупности.
Спектральная эффективность
Ширина полосы (или спектральная) эффективность схем модуляции M-PSK увеличивается с увеличением порядка модуляции M (в отличие, например, от M-FSK ):
- ρ = журнал 2 M 2 [бит / с ⋅ Гц] { displaystyle rho = { frac { log _ {2} M} {2}} quad [{ text {bits}} / { text {s }} cdot { text {Hz}}]}
То же соотношение сохраняется и для M-QAM.
Дифференциальная фазовая манипуляция (DPSK)
Дифференциальное кодирование
Дифференциальная фазовая манипуляция (DPSK) — это распространенная форма фазовой модуляции, которая передает данные путем изменения фазы несущей волны. Как упоминалось для BPSK и QPSK, существует неоднозначность фазы, если совокупность поворачивается некоторым эффектом в канал связи, через который проходит сигнал. Эту проблему можно решить, используя данные для изменения, а не для установки фазы.
Например, в дифференциально-кодированной BPSK двоичной «1» может быть передан путем добавления 180 ° к текущей фазе и двоичного «0» путем добавления 0 ° к текущей фазе. Другой вариант DPSK — это симметричная дифференциальная фазовая манипуляция, SDPSK, где кодирование будет составлять + 90 ° для «1» и -90 ° для «0».
В дифференциально кодированной QPSK (DQPSK) фазовые сдвиги составляют 0 °, 90 °, 180 °, -90 °, что соответствует данным «00», «01», «11», «10». Этот вид кодирования может быть демодулирован таким же образом, как и для недифференциальной PSK, но фазовые неоднозначности можно игнорировать. Таким образом, каждый принятый символ демодулируется в одну из точек M { displaystyle M}
Модулированный сигнал показан ниже как для DBPSK, так и для DQPSK, как описано выше. На рисунке предполагается, что сигнал начинается с нулевой фазы, и поэтому в обоих сигналах есть фазовый сдвиг в t = 0 { displaystyle t = 0}

Анализ показывает, что дифференциальное кодирование примерно вдвое увеличивает количество ошибок по сравнению с обычным M { displaystyle M}

Одно из самых популярных приложений DPSK — это стандарт Bluetooth, где π / 4 { displaystyle pi / 4}
Демодуляция

Для сигнала, который был закодирован дифференциально, существует очевидный альтернативный метод демодуляции. Вместо обычной демодуляции и игнорирования неоднозначности фазы несущей сравнивается фаза между двумя последовательными принятыми символами и используется для определения того, какими должны были быть данные. Когда дифференциальное кодирование используется таким образом, схема известна как дифференциальная фазовая манипуляция (DPSK). Обратите внимание, что это немного отличается от просто дифференциально кодированной PSK, поскольку при приеме принятые символы не декодируются один за другим в точки совокупности, а вместо этого напрямую сравниваются друг с другом.
Вызвать полученный символ в k { displaystyle k}



- r k = E s e j ϕ k + n k. { displaystyle r_ {k} = { sqrt {E_ {s}}} e ^ {j phi _ {k}} + n_ {k}.}
Переменная решения для k — 1 { displaystyle k-1}





- rkrk — 1 ∗ = E sej (φ k — φ k — 1) + E sej φ knk — 1 ∗ + E se — j φ k — 1 nk + nknk — 1 * { displaystyle r_ {k} r_ {k-1} ^ {*} = E_ {s} e ^ {j left ( varphi _ {k} — varphi _ {k-1} right) } + { sqrt {E_ {s}}} e ^ {j varphi _ {k}} n_ {k-1} ^ {*} + { sqrt {E_ {s}}} e ^ {- j varphi _ {k-1}} n_ {k} + n_ {k} n_ {k-1} ^ {*}}
где верхний индекс * обозначает комплексное сопряжение. В отсутствие шума фаза этого сигнала равна ϕ k — ϕ k — 1 { displaystyle phi _ {k} — phi _ {k-1}}
Вероятность ошибки для DPSK в целом трудно вычислить, но в случае DBPSK это:
- P b = 1 2 e — E b N 0, { displaystyle P_ {b } = { frac {1} {2}} e ^ {- { frac {E_ {b}} {N_ {0}}}},}
который при численной оценке лишь немного хуже обычного BPSK, особенно при более высоких значениях E b / N 0 { displaystyle E_ {b} / N_ {0}}
Использование DPSK устраняет необходимость в возможных сложных схемах восстановления несущей для обеспечения точной оценки фазы и может быть привлекательной альтернативой обычному PSK.
В оптической связи данные могут быть модулированы по фазе лазера дифференциальным способом. Модуляция представляет собой лазер, который излучает непрерывную волну, и модулятор Маха – Цендера, который принимает электрические двоичные данные. В случае BPSK лазер передает поле без изменений для двоичной «1» и с обратной полярностью для «0». Демодулятор состоит из интерферометра линии задержки, который задерживает один бит, поэтому два бита можно сравнивать за один раз. При дальнейшей обработке используется фотодиод для преобразования оптического поля в электрический ток, так что информация возвращается в исходное состояние.
Коэффициенты ошибок по битам DBPSK и DQPSK сравниваются с их недифференциальными аналогами на графике справа. Потери при использовании DBPSK достаточно малы по сравнению с уменьшением сложности, которое часто используется в системах связи, которые иначе использовали бы BPSK. Однако для DQPSK потеря производительности по сравнению с обычным QPSK больше, и разработчик системы должен сбалансировать это с уменьшением сложности.
Пример: BPSK с дифференциальным кодированием
Схема системы дифференциального кодирования / декодирования
В k th { displaystyle k ^ { textrm {th}}}



- ek = ek — 1 ⊕ bk { displaystyle , e_ {k} = e_ {k-1} oplus b_ {k}}
где ⊕ { displaystyle oplus {}}

Итак, ek { displaystyle e_ {k}}

Полученный сигнал демодулируется для получения ek = ± 1 { displaystyle e_ {k} = pm 1}
- bk = ek ⊕ ek — 1, { displaystyle b_ {k} = e_ {k} oplus e_ {k-1},}
поскольку двоичное вычитание аналогично двоичному сложению.
Следовательно, bk = 1 { displaystyle b_ {k} = 1}






Дифференциальные схемы для других модуляций PSK могут быть разработаны аналогичным образом. Формы сигналов для DPSK такие же, как для PSK с дифференциальным кодированием, приведенные выше, поскольку единственное изменение между двумя схемами — на приемнике.
Кривая BER для этого примера сравнивается с обычным BPSK справа. Как упоминалось выше, хотя частота ошибок увеличивается примерно вдвое, увеличение E b / N 0 { displaystyle E_ {b} / N_ {0}}

Взаимная информация с аддитивным белым гауссовским шумом

взаимная информация PSK может быть оценена в аддитивном гауссовском шуме посредством численного интегрирования его определения. Кривые взаимной информации насыщаются до количества битов, переносимых каждым символом в пределе бесконечного отношения сигнал / шум E s / N 0 { displaystyle E_ {s} / N_ {0}}
При промежуточных значениях отношения сигнал / шум взаимная информация (MI) хорошо аппроксимируется следующим образом:
- MI ≃ log 2 (4 π e E s N 0). { displaystyle { textrm {MI}} simeq log _ {2} left ({ sqrt {{ frac {4 pi} {e}} { frac {E_ {s}} {N_ {0) }}}}} right).}
Взаимная информация PSK по каналу AWGN обычно находится дальше от пропускной способности канала AWGN, чем форматы модуляции QAM.
См. Также
| Викискладе есть носители, относящиеся к Квантованной фазовой модуляции. |
Примечания
Ссылки
Обозначения и теоретические результаты в этой статье основаны на материалах, представленных в следующих источниках:
- Proakis, John G. (1995). Цифровая связь. Сингапур: Макгроу Хилл. ISBN 0-07-113814-5.
- Диван, Леон В. II (1997). Цифровая и аналоговая связь. Река Аппер Сэдл, Нью-Джерси: Прентис-Холл. ISBN 0-13-081223-4.
- Хайкин, Саймон (1988). Цифровые коммуникации. Торонто, Канада: John Wiley Sons. ISBN 0-471-62947-2.
-
Среды
-
Согласованная
фильтрация и -
фильтрация
по Найквисту -
Полная
система передачи данных -
Вероятности
символьной и битовой -
ошибки
для модуляционных схем -
Синхронизация
элементов сети
Согласованная
фильтрация и фильтрация по Найквисту.
фильтрация
по Найквисту
-
Временной
критерий Найквиста:
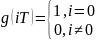
-
Частотный
критерий Найквиста:
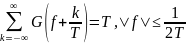
-
Для
простоты реализации, в качестве ФН
применяют т.н. фильтр «с приподнятым
косинусом»
(англ. raised cosine), имеющий полосу пропускания,
полосу задержки и спад между ними по 1
+ cos(f) (отсюда название)
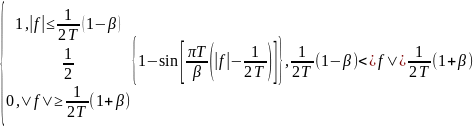
-
Коэффициент
β в диапазоне 0..1 определяет крутизну
перехода от полосы пропускания к полосе
задержки. Для
телефонных
модемов обычно β = 0.75
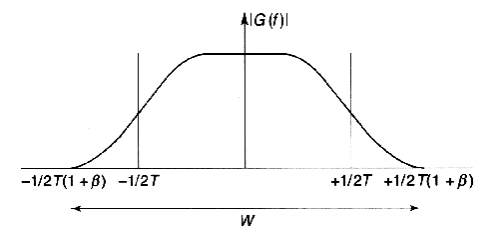
-
Занимаемая
сигналом полоса определяется β и:
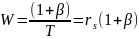
Согласованная
фильтрация
-
Для
верного обнаружения переданного
символа, на приемной стороне необходимо
максимизировать отношение сигнал/шум
для моментов измерения параметров
сигнала t
= i*T
(используем равенство Парсевал)
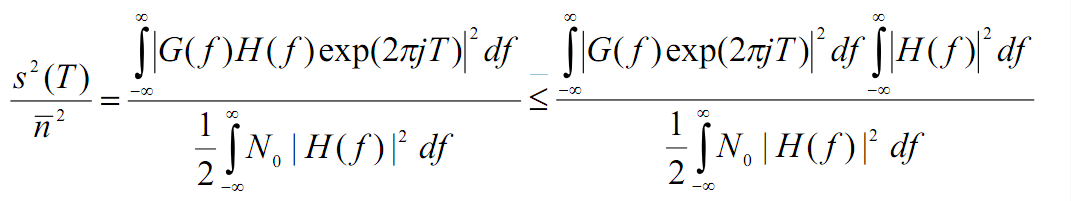
-
Здесь
используется неравенство Коши-Шварца,
которое в нашем случае становится
равенством при условии:
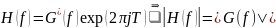
Согласованный
фильтр (СФ)
-
Фильтр
с частотной характеристикой, совпадающей
(согласованной) со спектром входного
сигнала называется СФ. Отношение
сигнал/шум на выходе СФ:
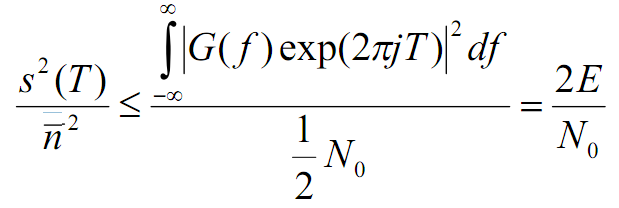
-
Импульсная
характеристика СФ обратна повремени
импульсу сигнала
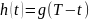
Полная
система передачи
-
Система
передачи данных, состоящая из приемника,
передатчика и линии связи, должна в
целом удовлетворять обоим критериям:
Найквиста и согласованной фильтрации -
Обозначая
частотные характеристики передатчика
и приемника T(f), R(f), и используя фильтр
«с приподнятым косинусом», получим
T(f) и R(f):
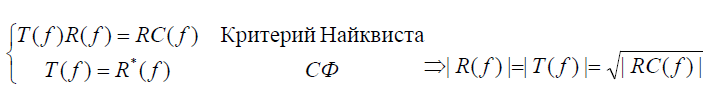
-
Полная
мощность принятого шума при использовании
такого фильтра для rb = 1/T:
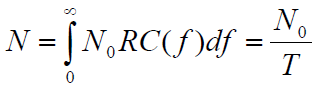
9) Расчет вероятностей символьной и битовой ошибки для модуляционных схем (bpsk, mpsk, qam). Основной подход, примеры.
Вероятность
битовой ошибки для BPSK
модуляции
Ошибка
возникает, когда np
> d/2
(см.созвездие). Тогда вероятность ошибки
определяется как:
n(t)
— гаус. сл. процесс: µ=0, P{n(t)>d/2}=Q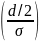
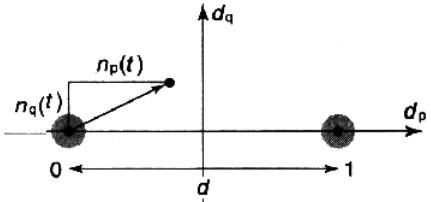
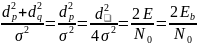
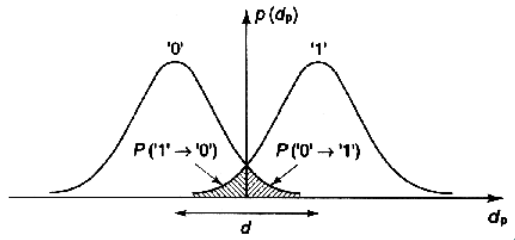
Вероятность
битовой ошибки для QPSK
модуляции
-
Энергетическая
эффективность QPSK аналогична BPSK, а
спектральная эффективность в 2 раза
выше.
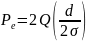
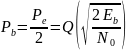
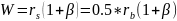
Вероятность
битовой ошибки для МPSK
модуляци
-
MPSK
модуляция определяет более 4-х фазовых
состояний (см. рис). -
Количество
состояний– степени 2, следовательно
символьная скорость в
k=log2M
меньше битовой
-
Определите
Pe
и Pb
для M=16, а также W для маркировки состояний
по Грею
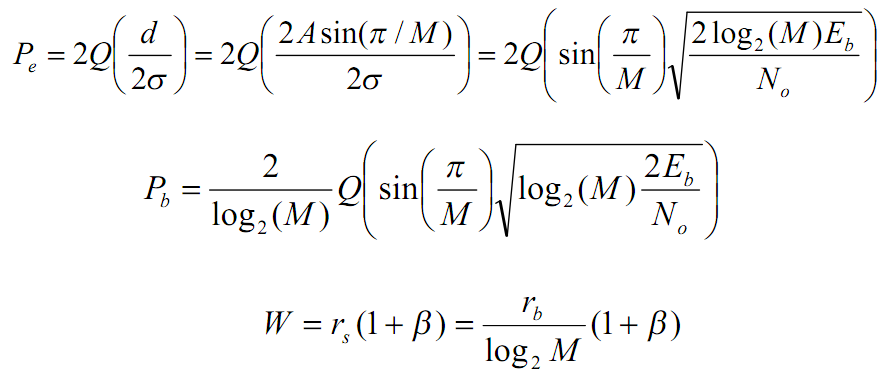
-
Энергетическая
эффективность MPSK
меньше BPSK,QPSK,
а спектральная эффективность выше.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
In digital transmission, the number of bit errors is the numbers of received bits of a data stream over a communication channel that have been altered due to noise, interference, distortion or bit synchronization errors.
The bit error rate (BER) is the number of bit errors per unit time. The bit error ratio (also BER) is the number of bit errors divided by the total number of transferred bits during a studied time interval. Bit error ratio is a unitless performance measure, often expressed as a percentage.[1]
The bit error probability pe is the expected value of the bit error ratio. The bit error ratio can be considered as an approximate estimate of the bit error probability. This estimate is accurate for a long time interval and a high number of bit errors.
Example[edit]
As an example, assume this transmitted bit sequence:
1 1 0 0 0 1 0 1 1
and the following received bit sequence:
0 1 0 1 0 1 0 0 1,
The number of bit errors (the underlined bits) is, in this case, 3. The BER is 3 incorrect bits divided by 9 transferred bits, resulting in a BER of 0.333 or 33.3%.
Packet error ratio[edit]
The packet error ratio (PER) is the number of incorrectly received data packets divided by the total number of received packets. A packet is declared incorrect if at least one bit is erroneous. The expectation value of the PER is denoted packet error probability pp, which for a data packet length of N bits can be expressed as
,
assuming that the bit errors are independent of each other. For small bit error probabilities and large data packets, this is approximately
Similar measurements can be carried out for the transmission of frames, blocks, or symbols.
The above expression can be rearranged to express the corresponding BER (pe) as a function of the PER (pp) and the data packet length N in bits:
Factors affecting the BER[edit]
In a communication system, the receiver side BER may be affected by transmission channel noise, interference, distortion, bit synchronization problems, attenuation, wireless multipath fading, etc.
The BER may be improved by choosing a strong signal strength (unless this causes cross-talk and more bit errors), by choosing a slow and robust modulation scheme or line coding scheme, and by applying channel coding schemes such as redundant forward error correction codes.
The transmission BER is the number of detected bits that are incorrect before error correction, divided by the total number of transferred bits (including redundant error codes). The information BER, approximately equal to the decoding error probability, is the number of decoded bits that remain incorrect after the error correction, divided by the total number of decoded bits (the useful information). Normally the transmission BER is larger than the information BER. The information BER is affected by the strength of the forward error correction code.
Analysis of the BER[edit]
The BER may be evaluated using stochastic (Monte Carlo) computer simulations. If a simple transmission channel model and data source model is assumed, the BER may also be calculated analytically. An example of such a data source model is the Bernoulli source.
Examples of simple channel models used in information theory are:
- Binary symmetric channel (used in analysis of decoding error probability in case of non-bursty bit errors on the transmission channel)
- Additive white Gaussian noise (AWGN) channel without fading.
A worst-case scenario is a completely random channel, where noise totally dominates over the useful signal. This results in a transmission BER of 50% (provided that a Bernoulli binary data source and a binary symmetrical channel are assumed, see below).
Bit-error rate curves for BPSK, QPSK, 8-PSK and 16-PSK, AWGN channel.
In a noisy channel, the BER is often expressed as a function of the normalized carrier-to-noise ratio measure denoted Eb/N0, (energy per bit to noise power spectral density ratio), or Es/N0 (energy per modulation symbol to noise spectral density).
For example, in the case of QPSK modulation and AWGN channel, the BER as function of the Eb/N0 is given by:

People usually plot the BER curves to describe the performance of a digital communication system. In optical communication, BER(dB) vs. Received Power(dBm) is usually used; while in wireless communication, BER(dB) vs. SNR(dB) is used.
Measuring the bit error ratio helps people choose the appropriate forward error correction codes. Since most such codes correct only bit-flips, but not bit-insertions or bit-deletions, the Hamming distance metric is the appropriate way to measure the number of bit errors. Many FEC coders also continuously measure the current BER.
A more general way of measuring the number of bit errors is the Levenshtein distance.
The Levenshtein distance measurement is more appropriate for measuring raw channel performance before frame synchronization, and when using error correction codes designed to correct bit-insertions and bit-deletions, such as Marker Codes and Watermark Codes.[3]
Mathematical draft[edit]
The BER is the likelihood of a bit misinterpretation due to electrical noise 





Knowing that the noise has a bilateral spectral density 


and 

Returning to BER, we have the likelihood of a bit misinterpretation 


where 

We can use the average energy of the signal 
±§
Bit error rate test[edit]
BERT or bit error rate test is a testing method for digital communication circuits that uses predetermined stress patterns consisting of a sequence of logical ones and zeros generated by a test pattern generator.
A BERT typically consists of a test pattern generator and a receiver that can be set to the same pattern. They can be used in pairs, with one at either end of a transmission link, or singularly at one end with a loopback at the remote end. BERTs are typically stand-alone specialised instruments, but can be personal computer–based. In use, the number of errors, if any, are counted and presented as a ratio such as 1 in 1,000,000, or 1 in 1e06.
Common types of BERT stress patterns[edit]
- PRBS (pseudorandom binary sequence) – A pseudorandom binary sequencer of N Bits. These pattern sequences are used to measure jitter and eye mask of TX-Data in electrical and optical data links.
- QRSS (quasi random signal source) – A pseudorandom binary sequencer which generates every combination of a 20-bit word, repeats every 1,048,575 words, and suppresses consecutive zeros to no more than 14. It contains high-density sequences, low-density sequences, and sequences that change from low to high and vice versa. This pattern is also the standard pattern used to measure jitter.
- 3 in 24 – Pattern contains the longest string of consecutive zeros (15) with the lowest ones density (12.5%). This pattern simultaneously stresses minimum ones density and the maximum number of consecutive zeros. The D4 frame format of 3 in 24 may cause a D4 yellow alarm for frame circuits depending on the alignment of one bits to a frame.
- 1:7 – Also referred to as 1 in 8. It has only a single one in an eight-bit repeating sequence. This pattern stresses the minimum ones density of 12.5% and should be used when testing facilities set for B8ZS coding as the 3 in 24 pattern increases to 29.5% when converted to B8ZS.
- Min/max – Pattern rapid sequence changes from low density to high density. Most useful when stressing the repeater’s ALBO feature.
- All ones (or mark) – A pattern composed of ones only. This pattern causes the repeater to consume the maximum amount of power. If DC to the repeater is regulated properly, the repeater will have no trouble transmitting the long ones sequence. This pattern should be used when measuring span power regulation. An unframed all ones pattern is used to indicate an AIS (also known as a blue alarm).
- All zeros – A pattern composed of zeros only. It is effective in finding equipment misoptioned for AMI, such as fiber/radio multiplex low-speed inputs.
- Alternating 0s and 1s — A pattern composed of alternating ones and zeroes.
- 2 in 8 – Pattern contains a maximum of four consecutive zeros. It will not invoke a B8ZS sequence because eight consecutive zeros are required to cause a B8ZS substitution. The pattern is effective in finding equipment misoptioned for B8ZS.
- Bridgetap — Bridge taps within a span can be detected by employing a number of test patterns with a variety of ones and zeros densities. This test generates 21 test patterns and runs for 15 minutes. If a signal error occurs, the span may have one or more bridge taps. This pattern is only effective for T1 spans that transmit the signal raw. Modulation used in HDSL spans negates the bridgetap patterns’ ability to uncover bridge taps.
- Multipat — This test generates five commonly used test patterns to allow DS1 span testing without having to select each test pattern individually. Patterns are: all ones, 1:7, 2 in 8, 3 in 24, and QRSS.
- T1-DALY and 55 OCTET — Each of these patterns contain fifty-five (55), eight bit octets of data in a sequence that changes rapidly between low and high density. These patterns are used primarily to stress the ALBO and equalizer circuitry but they will also stress timing recovery. 55 OCTET has fifteen (15) consecutive zeroes and can only be used unframed without violating one’s density requirements. For framed signals, the T1-DALY pattern should be used. Both patterns will force a B8ZS code in circuits optioned for B8ZS.
Bit error rate tester[edit]
A bit error rate tester (BERT), also known as a «bit error ratio tester»[4] or bit error rate test solution (BERTs) is electronic test equipment used to test the quality of signal transmission of single components or complete systems.
The main building blocks of a BERT are:
- Pattern generator, which transmits a defined test pattern to the DUT or test system
- Error detector connected to the DUT or test system, to count the errors generated by the DUT or test system
- Clock signal generator to synchronize the pattern generator and the error detector
- Digital communication analyser is optional to display the transmitted or received signal
- Electrical-optical converter and optical-electrical converter for testing optical communication signals
See also[edit]
- Burst error
- Error correction code
- Errored second
- Pseudo bit error ratio
- Viterbi Error Rate
References[edit]
- ^ Jit Lim (14 December 2010). «Is BER the bit error ratio or the bit error rate?». EDN. Retrieved 2015-02-16.
- ^
Digital Communications, John Proakis, Massoud Salehi, McGraw-Hill Education, Nov 6, 2007 - ^
«Keyboards and Covert Channels»
by Gaurav Shah, Andres Molina, and Matt Blaze (2006?) - ^ «Bit Error Rate Testing: BER Test BERT » Electronics Notes». www.electronics-notes.com. Retrieved 2020-04-11.
This article incorporates public domain material from Federal Standard 1037C. General Services Administration. (in support of MIL-STD-188).
External links[edit]
- QPSK BER for AWGN channel – online experiment


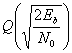
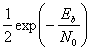
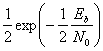



 .
.
 для двоичного «0»
для двоичного «0» для двоичной «1»
для двоичной «1»
 или P е = 1 2 erfc (E b N 0) { displaystyle P_ {e} = { frac {1} {2}} operatorname {erfc} left ({ sqrt { frac {E_ {b}}) {N_ {0}}}} right)}
или P е = 1 2 erfc (E b N 0) { displaystyle P_ {e} = { frac {1} {2}} operatorname {erfc} left ({ sqrt { frac {E_ {b}}) {N_ {0}}}} right)}



![{ displaysty le { begin {align} P_ {s} = 1- left (1-P_ {b} right) ^ {2} \ = 2Q left ({ sqrt { frac {E_ {s}) } {N_ {0}}}} right) - left [Q left ({ sqrt { frac {E_ {s}} {N_ {0}}}} right) right] ^ {2}. end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f83586ff4bc11f3ac6369902becbeba4313b675a)





![{ displaystyle rho = { frac { log _ {2} M} {2}} quad [{ text {bits}} / { text {s}} cdot { текст {Гц}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0750a97fea3020cd5bc401183d6ceb8b35dc51a3)






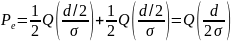
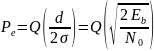


![{displaystyle p_{e}=1-{sqrt[{N}]{(1-p_{p})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5d380e45b0451c45265e199221fae5bd5b84bf9)
