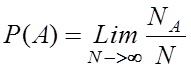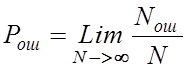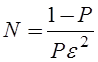При
оценке энергетического выигрыша
кодирования кодов, различающихся длиной
блока и кодовой скоростью, более удобной
оказывается характеристика
помехоустойчивости, выражаемая через
вероятность ошибки на двоичный символ
(бит).
Соотношение
между вероятностями ошибки декодирования
слова и ошибки на бит определяется
структурой порождающей матрицы
конкретного кода. Однако для обобщенного
анализа могут быть получены простые
границы для вероятности ошибки на бит.
Пусть длительность сеанса связи
составляет 1с. Тогда за сеанс связи может
быть передано 1/TW
кодовых слов, которые содержат k/TW
информационных символов. Количество
ошибочно принятых кодовых слов равно
PWk/TW.
Если через k0
обозначить количество ошибочно
принятых информационных символов при
каждом ошибочно принятом кодовом слове,
то вероятность ошибки на бит будет равна
. (3.19)
Проблема
заключается в определении величины k0.
В наихудшем случае ошибочный прием
кодового слова сопровождается ошибочным
приемом всех k
информационных символов. Тогда
получаем верхнюю границу
. (3.20)
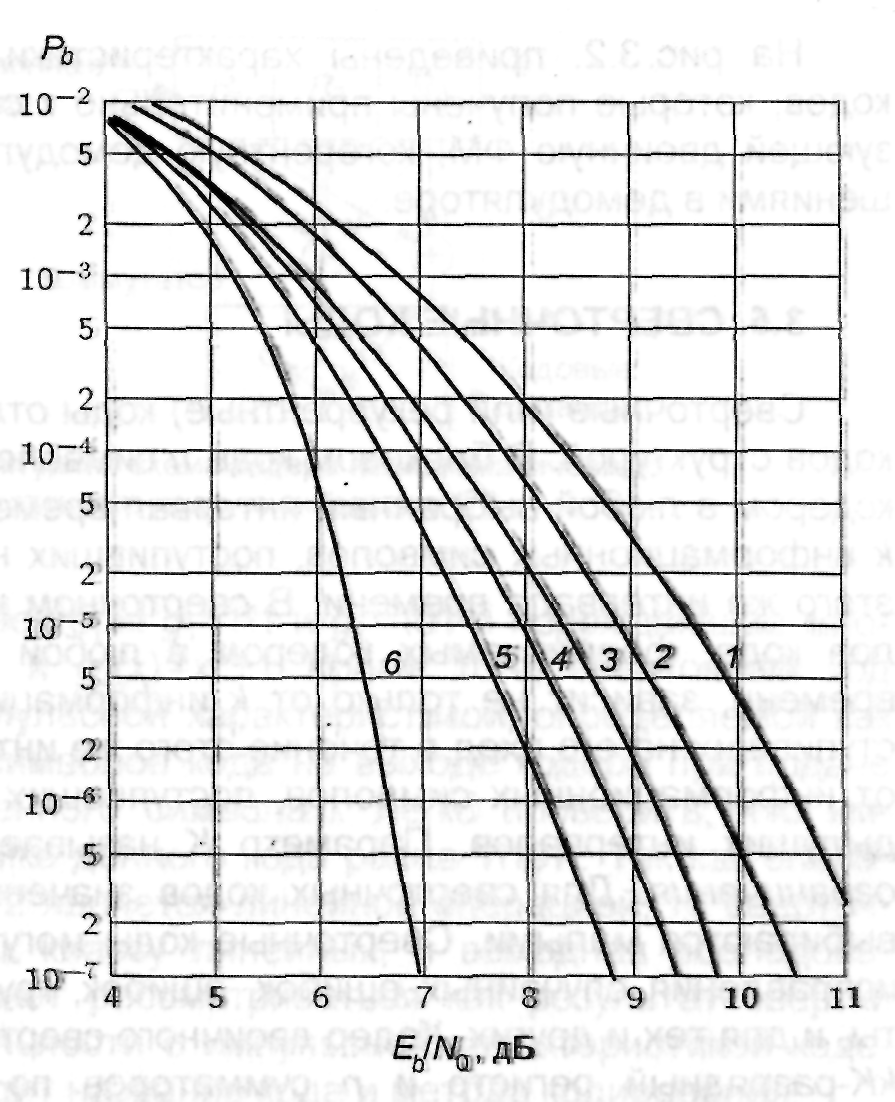
Рис.3.2.
Характеристики помехоустойчивости
блоковых кодов: 1 – без кодирования; 2 –
код Хэмминга (7, 4); 3 – код Хэмминга
(15, 11); 4 – код Хэмминга (31, 26); 5 – код
Голея (24, 12); 6 – код БЧХ (127, 64)
В
лучшем случае ошибочный прием кодового
слова приводит к единственной ошибке
в информационных символах. Поэтому для
нижней границы имеем k0=1
и
. (3.21)
Для
малых значений k
верхняя и нижняя границы становятся
строгими, и для оценки вероятности
ошибки на бит может быть использована
вероятность ошибочного приема слова.
Для высоких значений Eb/N0
вероятность ошибки на символ оказывается
чрезвычайно малой и ошибки при
декодировании кодовых слов с большой
вероятностью возникают при появлении
(t+1) ошибочных символов.
Из этих (t+1) ошибочных
символов в среднем (t+1)/n
относится к информационным. В результате
, (3.22)
. (3.23)
На
рис. 3.2. приведены характеристики
некоторых блоковых кодов, которые
получены применительно к системе связи,
использующей двоичную ФМ, когерентную
демодуляцию с жесткими решениями в
демодуляторе.
3.5. Сверточные коды
Сверточные
(или рекуррентные) коды отличаются от
блоковых кодов структурой. В блоковом
коде n символов кода, формируемых
кодером в любой выбранный интервал
времени, зависят только от k
информационных символов, поступивших
на его вход в течение этого же интервала
времени. В сверточном коде блок из n
символов кода, формируемых кодером
в любой выбранный интервал времени,
зависит не только от k
информационных символов, поступивших
на его вход в течение этого же интервала
времени, но и от информационных символов,
поступивших в течение (K–1)
предыдущих интервалов. Параметр K
называется длиной кодового
ограничения. Для сверточных кодов
значение параметров n и k
выбираются малыми. Сверточные коды
могут использоваться для исправления
случайных ошибок, ошибок, группирующихся
в пакеты, и для тех и других. Кодер
двоичного сверточиого кода содержит
kK-разрядный регистр
и n сумматоров по mod
2. Обобщенная структурная схема кодера
сверточного кода приведена на рис.3.3.
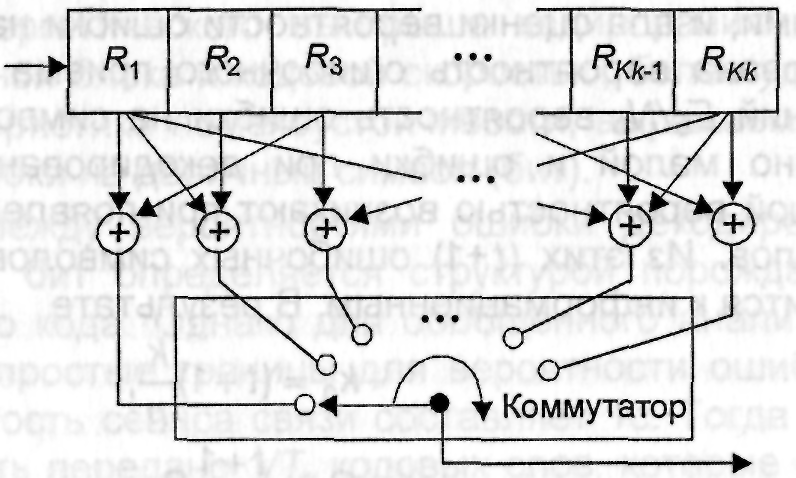
Рис.
3.3. Обобщенная структурная схема
кодера сверточного кода
На
рис. 3.4 приведены пример кодера сверточного
кода с параметрами k =1,
n = 2,
K = 3,
Rk = 1/2.
Информационные символы поступают на
вход регистра, а символы кода формируются
на выходе коммутатора. Коммутатор (КМ)
последовательно опрашивает выходы
сумматоров по mod 2 в течение
интервала времени, равного длительности
информационного символа (бита).
Схема
подключения сумматоров по mod
2, значения k, n и K
полностью описывают сверточный код. Их
можно определить с помощью генераторных
векторов или многочленов. Например,
сверточный код, формируемый кодером,
изображенным на рис.3.4,
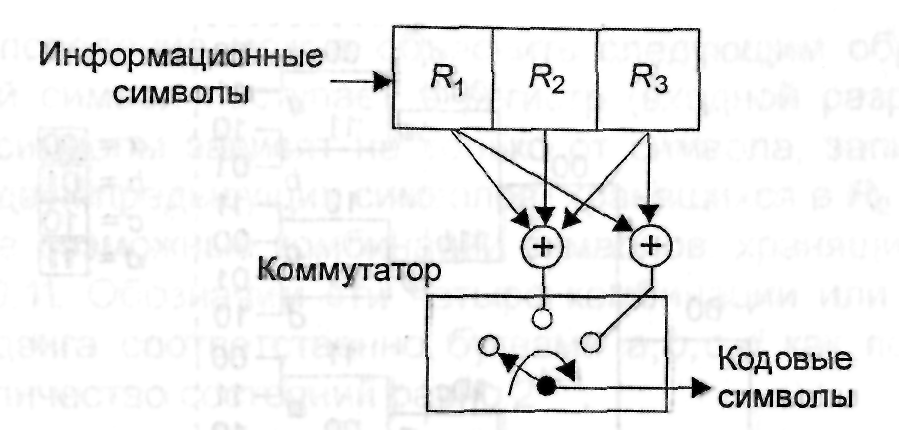
Рис.
3.4. Структурная
схема кодера несистематического
сверточного кода со скоростью 1/2
Информационные
символы имеет порождающие векторы
g1 = 111
и g2 = 101
и порождающие многочлены g1(х) = х2+х+1
и g2(х)=х2+1.
Кроме того, сверточный код может быть
задан импульсной характеристикой,
определяемой как последовательность
символов кода на выходе кодера при
подаче на его вход единственного символа
1. Легко проверить, что импульсная
характеристика данного кода равна
111011. Так как операция сложения по mod
2 является линейной операцией, то
сверточные коды относятся к классу
линейных, и выходная последовательность
кодера может рассматриваться как
результат свертки входной последовательности
с импульсной характеристикой кодера.
Отсюда и происходит название кода и
метода кодирования.
Процедуры
кодирования и декодирования удобно
описывать с помощью так называемого
кодового дерева, которое отображает
последовательности на выходе кодера
для любой возможной входной
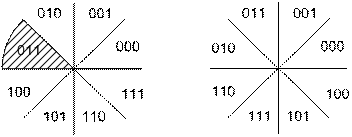
последовательности. На рис. 3.5 приведено
кодовое дерево кодера, изображенного
на рис. 3.4, для блока из пяти информационных
символов. Если первый символ принимает
значение 0, то на выходе кодера формируется
пара символов 00. Если первый символ
принимает значение 1, то на выходе кодера
формируется пара символов 11. Это показано
с помощью двух ветвей, которые выходят
из начального узла. Верхняя ветвь
соответствует 0, нижняя – 1. В каждом из
последующих узлов ветвление происходит
аналогичным образом: из каждого узла
исходит две ветви, причем верхняя ветвь
соответствует 0, а нижняя – 1. Ветвление
будет происходить вплоть до последнего
символа входного блока. Вслед за ним
все входные символы принимают значение
0, и образуется только одна обрывающаяся
ветвь. Таким образом, каждой из возможных
входных комбинаций информационных
символов соответствует своя вершина
на кодовом дереве. В данном случае
имеется 32 вершины. С помощью кодового
дерева легко построить выходную
последовательность символов кода,
соответствующую определенной входной
последовательности. Например, входной
последовательности 11010 соответствует
выходная последовательность, лежащая
на пути, изображенном пунктирной линией.

Рис.3.5.
Кодовое дерево для кодера, изображенного
на рис. 3.4
Анализируя
структуру кодового дерева на рис. 3.5,
можно заметить, что, начиная с узлов
третьего уровня, она носит повторяющийся
характер. Действительно, группа ветвей,
заключенных в прямоугольники, изображенные
пунктирными линиями, полностью совпадают.
Это означает, что при поступлении на
вход четвертого символа выходной символ
кода будет одним и тем же, независимо
от того, каким был первый входной символ:
0 или 1. Другими словами, после первых
трех групп выходных символов кода
входные последовательности 1x1x2x3x4…
и 0x1x2x3x4…
будут порождать один и тот же выходной
символ.
Обозначим
четыре узла третьего уровня, т.е. узлы,
в которых происходит третье ветвление,
буквами a,b,c,d.
Повторяющаяся структура ветвей имеет
место и для узлов четвертого и пятого
уровней, поэтому их также можно обозначить
этими же буквами. Для узлов пятого уровня
любой из четырех комбинаций (11,10,01, 00)
первых двух входных символов будет
соответствовать один и тот же выходной
символ.
Такое
поведение можно объяснить следующим
образом. Когда входной символ поступает
в регистр (входной разряд R1),
то выходные символы зависят не только
от символа, записанного в R1,
но и от двух предыдущих символов,
хранящихся в R2
и R3.
Имеется четыре возможные комбинации
символов, хранящихся в R2
и R3:
00, 01, 10, 11. Обозначим эти четыре комбинации
или состояния регистра сдвига
соответственно буквами a,
b, c,
d как показано на
рис. 3.5. Количество состояний равно 2K–1.
Входные
символы 0 и 1 будут формировать четыре
различные комбинации выходных символов
в зависимости от состояния кодера. Если
входной символ 0, то на выходе декодера
будут формироваться 00, 10, 11 или 01 в
зависимости от того, в каком состоянии
находился кодер: a, b,
c или d.
To же самое правило можно
применить относительно символа 1.
Таким
образом, поведение кодера можно полностью
описать с помощью диаграммы состояний,
изображенной на рис. 3.6, а или
направленного графа с четырьмя состояниями
(рис. 3.6, б) который устанавливает
однозначное соответствие между входными
и выходными символами кодера. На графе
сплошные линии соответствуют входному
символу 0, а пунктирные – символу 1.
Например, если кодер находится в состоянии
а и на вход поступает 1, то на выходе
декодера будет формироваться комбинация
11 (пунктирная линия) и декодер перейдет
в состояние b,
соответствующее R3 = 0
и R2 = 1
– Аналогичным образом при поступлении
0 декодер останется в состоянии а
(сплошная линия) и на выходе будет
формироваться комбинация 00.
Заметим,
что прямой переход из состояния а в
состояние с или d
невозможен, причем из любого состояния
прямой переход возможен только в одно
из двух состояний. Диаграмма состояний
содержит исчерпывающую информацию о
структуре кодового дерева.
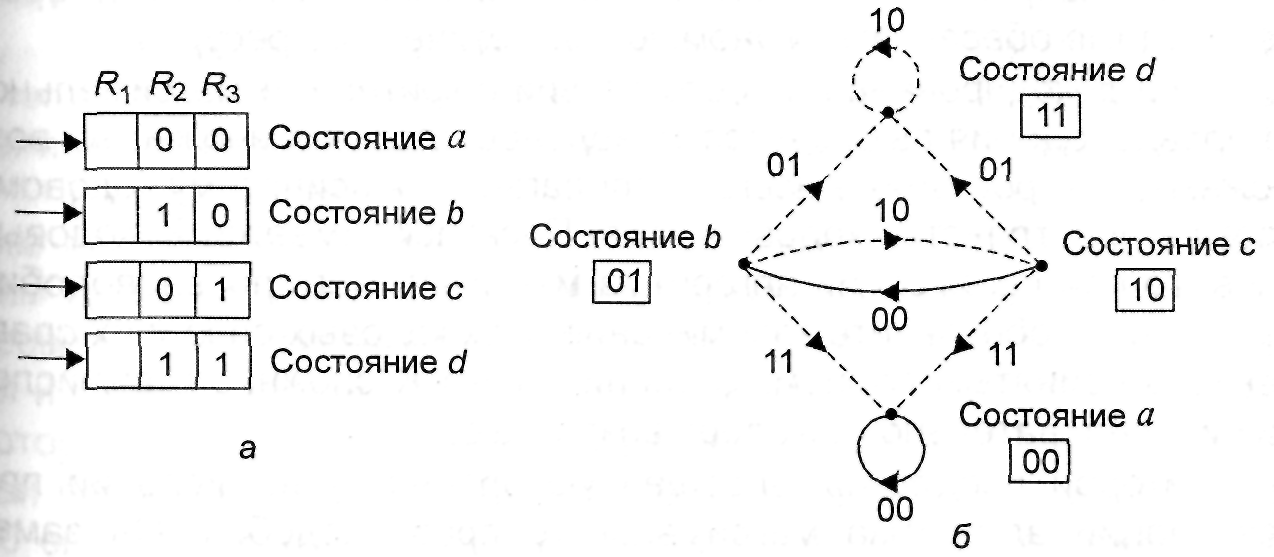
Рис.
3.6. Диаграмма состояний для кодера,
изображенного на рис. 3.4
Другим
полезным способом описания кодового
дерева является решетчатая диаграмма,
изображенная на рис. 3.7. Диаграмма берет
начало из состояния а и на ней
отображаются все возможные переходы
при поступлении на вход очередного
символа. Сплошным линиям соответствуют
переходы, происходящие при поступлении
символа 1 пунктирным – символа 0. При
поступлении на вход двух символов кодер
оказывается в одном из четырех состояний:
a, b,
c или d.
Заметим, что решетчатая диаграмма имеет
повторяющийся характер и может быть
легко построена с помощью диаграммы
состояний.
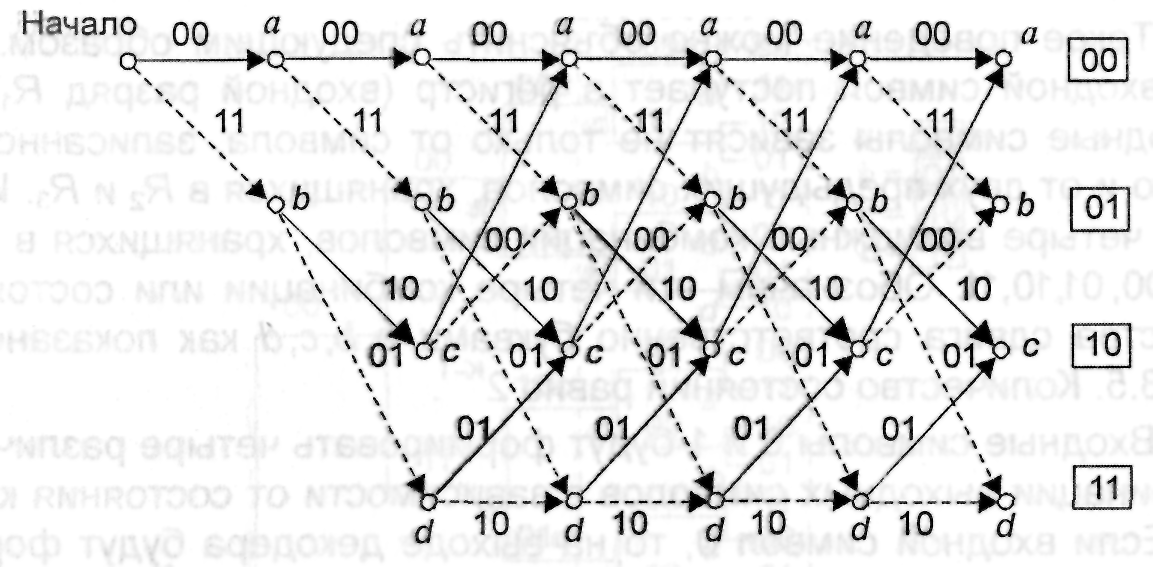
Рис.
3.7. Решетчатая диаграмма для кодера,
изображенного на рис.3.4
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
26.02.2016541.64 Кб17Сертификат Реконструкция жизни.PDF
- #
- #
- #
- #
- #
- #
Кодирование Рида-Соломона для чайников
Время на прочтение
14 мин
Количество просмотров 17K
Есть способ передавать данные, теряя часть по пути, но так, чтобы потерянное можно было вернуть по прибытии. Это третья, завершающая часть моего простого изложения алгоритма избыточного кодирования по Риду-Соломону. Реализовать это в коде не прочитав первую, или хотя бы вторую часть на эту тему будет проблематично, но чтобы понять для себя что можно сделать с использованием кодировки Рида-Соломона, можно ограничиться прочтением этой статьи.
Что может этот код?
Итак, что из себя представляет избыточный код Рида-Соломона с практической точки зрения? Допустим, есть у нас сообщение – «DON’T PANIC». Если добавить к нему несколько избыточных байт, допустим 6 штук: «rrrrrrDON’T PANIC» (каждый r – это рассчитанный по алгоритму байт), а затем передать через какую-нибудь среду с помехами, или сохранить там, где данные могут понемногу портиться, то по окончании передачи или хранения у нас может остаться такое, например: «rrrrrrDON’AAAAAAA» (6 байт оказались с ошибкой). Если мы знаем номера байтов, где вместо букв, которые были при создании кода, вдруг оказались какие-нибудь «A», то мы можем полностью восстановить сообщение в исходное «rrrrrrDON’T PANIC». После этого можно для красоты убрать избыточные символы. Теперь текст можно печатать на обложку.
Вообще, избыточных символов к сообщению мы можем добавить сколько угодно. Количество избыточных символов равно количеству исправляемых ошибок (это верно лишь в том случае, когда нам известны номера позиций ошибок). Как правило, ошибки, положение которых известно, называют erasures. Благозвучного перевода найти не могу («стирание» мне не кажется благозвучным), так что в дальнейшем я буду применять термин «опечатки» и ставить его в кавычки (прекрасно понимаю, что этот термин обычно несёт похожий, но другой смысл). Исправление «опечаток» полезно, например, при восстановлении блоков QR кода, которые по какой-либо причине не удалось прочитать.
Также код Рида-Соломона позволяет исправлять ошибки, положение которых неизвестно, но тогда на каждую одну исправляемую ошибку должно приходиться 2 избыточных символа. «rrrrrrDON’T PANIC», принятые как «rrrrrrDO___ PANIC» легко будут исправлены без дополнительной информации. Неправильно принятый байт, положение которого неизвестно, в дальнейшем я буду называть «ошибкой» и тоже брать в кавычки.
Можно комбинировать исправление «ошибок» и «опечаток». Если, например, есть 3 избыточных символа, то можно исправить одну «ошибку» и одну «опечатку». Ещё раз обращу внимание на то, что чтобы исправить «опечатку», нужно каким-то образом (не связанным с алгоритмом Рида-Соломона) узнать номер байта «опечатки». Что важно, и «ошибки» и «опечатки» могут быть исправлены алгоритмом и в избыточных байтах тоже.
Стоит отметить, что если количество переданных и принятых байт отличается, то здесь код Рида-Соломона практически бессилен. То есть, если на расшифровку попадёт такое: «rrrrrrDO’AIC», то ничего сделать не получится, если, конечно, неизвестно какие позиции у пропавших букв.
Как закодировать сообщение?
Здесь уже не обойтись без понимания арифметики с полиномами в полях Галуа. Ранее мы научились представлять сообщения в виде полиномов и проводить операции сложения, умножения и деления над ними. Уже этого почти достаточно, чтобы создать код Рида-Соломона из сообщения. Единственно, для того, чтобы это сделать понадобится ещё полином-генератор. Это результат такого произведения:
Где – это примитивный член поля (как правило, выбирают 2), а
– это количество избыточных символов. То есть, прежде чем создавать код Рида-Соломона из сообщения, нужно определиться с количеством избыточных символов, которое мы считаем достаточным, затем перемножить биномы вида
в количестве
штук по правилам перемножения полиномов. Для любого сообщения можно использовать один и тот же полином-генератор, и любое сообщение в таком случае будет закодировано с одним и тем же количеством избыточных символов.
Пример: Мы решили использовать 4 избыточных символа, тогда нужно составить такое выражение:
Так как мы работаем с полем Галуа с характеристикой 2, то вместо минуса можно смело писать плюс, не боясь никаких последствий. Жаль, что это не работает с количеством денег после похода в магазин. Итак, возводим в степень, и перемножаем (по правилам поля Галуа GF[256], порождающий полином 285):
Необязательное дополнение
Легко заметить (правда легко – надо лишь взглянуть на произведение биномов), что корнями получившегося полинома будут как раз степени примитивного члена: 2, 4, 8, 16. Что самое интересное, если взять какой-нибудь другой полином, умножить его на (4 – в данном случае это количество избыточных символов), получится тот же самый полином, только с нулями в коэффициентах перед первыми 4 младшими степенями, а затем разделить его на полином-генератор, и прибавить остаток от деления к нашему полиному с 4 нулями, то его корнями также будут эти 4 числа (2, 4, 8, 16).
Выражение выше есть полином-генератор, который необходим для того, чтобы закодировать сообщение любой длины, добавив к нему 4 избыточных символа, которые позволят скорректировать 2 «ошибки» или 4 «опечатки».
Прежде чем приводить пример кодирования, нужно договориться об обозначениях. Полиномы, записанные «по-математически» с иксами и степенями выглядят довольно-таки громоздко. На самом деле, при написании программы достаточно знать коэффициенты полинома, а степени можно узнать из положения этих коэффициентов. Таким образом полученный в примере выше полином-генератор можно записать так: {116, 231, 216, 30, 1}. Также, для ещё большей компактности, можно опустить скобки и запятые и записать всё в шестнадцатеричном представлении: 74 E7 D8 1E 01. Выходит в 2 раза короче. Надо отметить, что если в «математической» записи мы не пишем члены, коэффициенты которых равны нулю, то при принятой здесь шестнадцатеричной записи они обязательны, и, например,
нужно записывать так:
или 00 00 00 00 0A. Там, где «математическая» запись позволит более понятно объяснить суть, я буду прибегать к ней.
Итак, чтобы представить сообщение «DON’T PANIC» в полиномиальной форме, с учётом соглашения выше достаточно просто записать его байты:
44 4F 4E 27 54 20 50 41 4E 49 43.
Чтобы создать код Рида-Соломона с 4 избыточными символами, сдвигаем полином вправо на 4 позиции (что эквивалентно умножению его на ):
00 00 00 00 44 4F 4E 27 54 20 50 41 4E 49 43
Теперь делим полученный полином на полином-генератор (74 E7 D8 1E 01), берём остаток от деления (DB 22 58 5C) и записываем вместо нулей к полиному, который мы делили. (это эквивалентно операции сложения):
DB 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 43
Вот эта строка как раз и будет кодом Рида-Соломона для сообщения «DON’T PANIC» с 4 избыточными символами.
Некоторые пояснения
Порядок записи степеней при представлении сообщения в виде полинома имеет значение, ведь полином не эквивалентен полиному
, поэтому следует определиться с этим порядком один раз и его придерживаться. Ещё раз: когда мы преобразуем:
сообщение -> полином, порядок имеет значение.
Так как избыточные символы подставляются именно в младшие степени при кодировании, то от выбора порядка степеней при представлении сообщения зависит положение избыточных символов – в начале или в конце закодированного сообщения.
Изменение порядка записи никоим образом не влияет на арифметику с полиномами, ведь как полином не запиши другим он не становится. . Это очевидно, но при составлении алгоритма легко запутаться.
В некоторых статьях полином-генератор начинается не с первой степени, как здесь: , а с нулевой:
. Это не эквивалентные записи одного и того же, последующие вычисления будут отличаться в зависимости от этого выбора.
Также при создании кода можно не делить на полином-генератор, получая остаток, а умножать на него. Это слегка другая разновидность кода Рида-Соломона, в которой в закодированном сообщении не содержится в явном виде исходное.
Как раскодировать сообщение?
Здесь всё посложнее будет. Ненамного, но всё же. Вопрос про раскодировать, собственно «не вопрос!» – убираем избыточные символы и остаётся исходное сообщение. Вопрос в том, как узнать, были ли ошибки при передаче, и если были, то как их исправить.
В первую очередь нужно отметить, что при проверке на наличие ошибок нужно знать количество избыточных символов. А во-вторую – надо научиться считать значение полинома при определённом . Про количество избыточных символов нам должен заранее сообщить тот, кто кодировал сообщение, а вот чтобы вычислить значение полинома нужно написать ещё одну функцию для работы с полиномами. Это элементарщина – просто вместо
подставляется нужное значение. Но пример, всё же, никогда не помешает.
Пример: Нужно вычислить полиномпри
. Подставляем, возводим в степень:
, перемножаем,
, складываем и получаем число
. Сложение, умножение и возведение в степень здесь по правилам поля Галуа GF[256] (порождающий полином 285)
Код приводить не буду, оставлю ссылку на гитхаб. Там всё что я описывал в этой и предыдущих статьях реализовано на C#, в виде демо-приложения (собирается под win в VS2019, бинарник тоже выложен). Можно посмотреть как работает арифметика в поле Галуа, а также посмотреть, как работает кодирование Рида-Соломона.
Итак, прежде чем исправлять «ошибки» или «опечатки» нужно узнать есть ли они. Элементарно. Нужно вычислить полином принятого сообщения с избыточными символами при равном степеням примитивного члена. Это те же числа, которые мы использовали при составлении полинома-генератора:
,
– количество избыточных символов,
– примитивный член. Если ошибок нет, то все вычисленные значения будут равны нулю. Закодированное ранее сообщение «DON’T PANIC» с 4 избыточными символами, в виде полинома в шестнадцатеричном представлении:
DB 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 43,
если вычислить этот полином при равном 2, 4, 8, 16, то получатся значения: 0, 0, 0, 0, ведь здесь сообщение точно в таком же виде, в котором оно и было закодировано. Если изменить хотя бы один байт, например, последний символ сделаем более правильным: 42 вместо 43:
DB 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 42,
то результат такого же вычисления станет равным 13, 18, B5, 5D. Эти значения называются синдромами. Их тоже можно принять за полином. Тогда это будет полином синдромов.
Итак, чтобы узнать есть ли ошибки в принятом сообщении, нужно посчитать полином синдромов. Если он состоит из одних нулей (также можно говорить, что он равен нулю), то ошибок нет.
Важное, но совсем занудное дополнение
Может случиться так, что сообщение с ошибками будет иметь синдром равным нулю. Это случится в том случае, когда полином амплитуд ошибок (о нём будет ниже) кратен полиному-генератору. Так что проверку ошибок по полиному синдромов кода Рида-Соломона нельзя считать 100% гарантией отсутствия ошибок. Можно даже посчитать вероятность такого случая.
Допустим мы кодируем сообщение из 4 символов четырьмя же избыточными символами, то есть передаём 8 байт. Также возьмём для примера вероятность ошибки при передаче одного символа в 10%. То есть, в среднем на каждые 10 символов приходится один, который передался как случайное число от 00 до FF. Это, конечно же совсем синтетическая ситуация, которая вряд ли будет в реальности, но здесь можно точно вычислить вероятности.
Для рассчёта я рассуждаю так: Полиномы, кратные полиному-генератору получаются умножением генератора на другие полиномы. Пятизначный кратный полином — получается умножением на константу от 1 до 255. Шестизначный — умножением на бином первой степени а их, без нулей ровно Те же рассуждения для 7 и 8 -значных полиномов, кратных генератору. Затем надо найти вероятности выпадения 5, 6, 7 и 8 ошибок подряд, и для каждой из них вычислить вероятность, что такая случайная последовательность ошибок окажется кратной полиному-генератору. Сложить их, и тогда мы получим вероятность того, что при передаче 4 байт с 4 избыточными символами, при вероятности ошибки при передаче одного символа 10% получится не обнаруживаемая кодом Рида-Соломона ошибочная передача. Рассчёт в маткаде:
Итого, на каждые ~500 Тб при такой передаче окажется один блок из 4 ошибочных символов, которые алгоритм посчитает корректными. Цифры большие, но вероятность не 0. При вероятности ошибки в 1% речь идёт об эксабайтах. Рассчёт, конечно не эталон, может быть даже с ошибками, но даёт понять об порядках чисел.
Что же делать, если синдром не равен нулю? Конечно же исправлять ошибки! Для начала рассмотрим случай с «опечатками», когда мы точно знаем номера позиций некорректно принятых байт. Ошибёмся намеренно в нашем закодированном сообщении 4 раза, столько же, сколько у нас избыточных символов:
DB 22 58 5C 44 4F 4E 27 54 20 41 41 41 41 41
41 – это буква A, поэтому их 5 подряд получилось. Позиции ошибок считаются слева направо, начиная с 0. Для удобства используем шестнадцатеричную систему при нумерации:
00 01 02 03 04 05 06 07 08 09 0A 0B 0C 0D 0E
DB 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 43
DB 22 58 5C 44 4F 4E 27 54 20 41 41 41 41 41
Позиции ошибок: 0A 0C 0D 0E.
Итак, если мы находимся на стороне приёмника, то у нас есть следующая информация:
-
Сообщение с 4 избыточными символами;
-
само сообщение: DB 22 58 5C 44 4F 4E 27 54 20 41 41 41 41 41;
-
В сообщении есть ошибки в позициях 0A 0C 0D 0E.
Этого достаточно, чтобы восстановить сообщение в исходное состояние. Но обо всём по порядку.
Для продолжения необходимо разучить ещё одну операцию с полиномами в полях Галуа — взятие формальной производной от полинома. Формальная производная полинома в поле Галуа похожа на обычную производную. Формальной она называется потому, что в полях вроде GF[256] нет дробных чисел, и соответственно нельзя определить производную, как отношение бесконечно малых величин. Вычисляется похоже на обычную производную, но с особенностями. Если при обычном дифференцировании , то для формальной производной в поле Галуа с основанием 2, формула для дифференцирования члена такая:
. Это значит, что достаточно просто переписать полином, начиная с первой степени (нулевая выкидывается) и у оставшегося убрать (обнулить, извиняюсь) члены с нечётными степенями. Пример:
Необходимо найти производную
(Это рандомный полином, не связан с примером). Производная суммы равна сумме производных, соответственно применяем формулу для производной члена и получаем:
Или, если записывать в шестнадцатеричном виде, то это же самое выглядит так:
(01 2D A5 C6 8C DF )’ = 2D 00 C6 00 DF .
Думаю, что из примера в шестнадцатеричном виде проще всего составить алгоритм нахождения формальной производной.
Теперь можно уже исправить «опечатки»? Как бы не так! Нужно ещё два полинома. Полином-локатор и полином ошибок.
Полином-локатор – это полином, корнями которого являются числа обратные примитивному члену в степени позиции ошибки. Сложно? Можно проще. Полином-локатор это произведение вида
где – это примитивный член,
и так далее – это позиции ошибок.
Пример: у нас есть позиции ошибок 10, 12, 13, 14; примитивный член тогда полином локатор будет таким:
Перемножаем и получаем полином-локатор для позиций ошибок 10, 12, 13, 14:
Или в шестнадцатеричной записи: 01 2D A5 C6 8C.
Про полином-локатор нужно понять следующее: из него можно получить позиции ошибок, и наоборот – из позиций ошибок можно получить полином-локатор. По сути, это две разные записи одного и того же – позиций ошибок.
Полином ошибок – его по-разному называют в разных статьях, он не так уж и сложен. Представляет из себя произведение полинома синдромов и полином-локатора, с отброшенными старшими степенями. Продолжая пример, найдём полином ошибок для искажённого сообщения:
DB 22 58 5C 44 4F 4E 27 54 20 41 41 41 41 41
Полином синдромов: 72 BD 22 5B
Произведение полинома синдромов и полинома-локатора не буду расписывать в «математическом» виде, напишу так:
(72 BD 22 5B)(01 2D A5 C6 8C) = 72 4B 10 22 D9 C0 57 15
У результата оставляем количество младших членов, равное количеству избыточных символов, в нашем случае их 4, старшие степени просто выбрасываем, они не нужны. Остаётся
72 4B 10 22
Это и есть полином ошибок.
Осталось посчитать амплитуды ошибок. Звучит угрожающе, но на деле это просто значения, которые нужно прибавить к искажённым символам сообщения чтобы получились неискажённые символы. Для этого воспользуемся алгоритмом Форни. Здесь придётся привести фрагмент кода, словами расписать так, чтобы было понятно, очень сложно.
Функция принимает на входе
-
полином синдромов (Syndromes),
-
полином, в котором члены – позиции ошибок (ErrPos),
-
количество избыточных символов (NumOfErCorrSymbs).
Класс GF_Byte — это просто байт, для которого переопределены арифметические операции так, чтобы они выполнялись по правилам поля Галуа GF[256], класс GF_Poly – Это полином в поле Галуа. По сути, массив GF_Byte. Для него также переопределны арифметические операции так, чтобы они выполнялись по правилам арифметики с полиномами в полях Галуа.
public static GF_Poly FindMagnitudesFromErrPos(
GF_Poly Syndromes,
GF_Poly ErrPos,
uint NumOfErCorrSymbs)
{
//Вычисление локатора из позиций ошибок
GF_Poly Locator = CalcLocatorPoly(ErrPos);
//Произведение для вычисления полинома ошибок
GF_Poly Product = Syndromes * Locator;
//Полином ошибок. DiscardHiDeg оставляет указаное количество младших степеней
GF_Poly ErrPoly = Product.DiscardHiDeg(NumOfErCorrSymbs);
//Производная локатора
GF_Poly LocatorDer = Locator.FormalDerivative();
//Здесь будут амплитуды ошибок. Количество членов - это самая большая позиция ошибки
GF_Poly Magnitudes = new GF_Poly(ErrPos.GetMaxCoef());
//Перебор каждой заданной позиции ошибки
for (uint i = 0; i < ErrPos.Len; i++) {
//число обратное примитивному члену в степени позиции ошибки
GF_Byte Xi = 1 / GF_Byte.Pow_a(ErrPos[i]);
//значение полинома ошибок при x = Xi
GF_Byte W = ErrPoly.Eval(Xi);
//значение производной локатора при x = Xi
GF_Byte L = LocatorDer.Eval(Xi);
//Это как раз и будет найденное значение ошибки,
//которое надо вычесть из ошибочного символа, чтобы он стал не ошибочным
GF_Byte Magnitude = W / L;
//запоминаем найденную амплитуду в текущей позиции ошибки
Magnitudes[ErrPos[i]] = Magnitude;
}
return Magnitudes;
}Если скормить функции следующие параметры:
-
полином синдромов 72 BD 22 5B
-
полином, в котором члены — позиции ошибок 0A 0C 0D 0E
-
количество символов коррекции ошибок 4,
то на выходе она даст полином амплитуд ошибок:
00 00 00 00 00 00 00 00 00 00 11 00 0F 08 02.
Теперь можно прибавить полученное к искажённому сообщению
DB 22 58 5C 44 4F 4E 27 54 20 41 41 41 41 41
(по правилам сложения полиномов, конечно же), и на выходе получится исходное сообщение:
DB 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 43.
Первые 4 байта — это избыточные символы. Если бы в них оказались «опечатки», то разницы никакой для алгоритма нет, разве что они нам не нужны после исправления. Можно их просто отбросить:
44 4F 4E 27 54 20 50 41 4E 49 43 Это исходное сообщение «DON’T PANIC».
Здесь должно быть понятно, как исправлять ошибки, положение которых известно. Само по себе уже это может нести практическую пользу. В QR кодах на обшарпанных стенах могут стереться некоторые квадратики, и программа, которая их расшифровывает сможет определить в каких именно местах находятся байты, которые не удалось прочитать, которые «стёрлись» – erasures, или как мы договорились писать по-русски «опечатки». Но нам этого, конечно же недостаточно. Мы хотим уметь выявлять испорченные байты без дополнительной информации, чтобы передавать их по радио, или по лазерному лучу, или записывать на диски (кого я обманываю? CD давно мертвы), может быть, захотим реализовать передачу через ультразвук под водой, чтобы управлять моделью подводной лодки, а какие-нибудь неблагодарные дельфины будут портить случайные данные своими песнями. Для всего этого нам понадобится уметь выявлять, в каких именно байтах при передаче попортились биты.
Как найти позиции ошибок?
Вспомним про полином-локатор. Его можно составить из заранее известных позиций ошибок, а ещё его можно вычислить из полинома-синдромов и количества избыточных символов. Есть не один алгоритм, который позволяет это сделать. Здесь будет алгоритм алгоритм Берлекэмпа-Мэсси. Если хочется много математики, то гугл с википедией на неё не скупятся. Я, если честно, не вник до конца в циклические полиномы и прочее-прочее-прочее. Стыдно, немножко, конечно, но я взял реализацию этого алгоритма с сайта Wikiversity переписал его на C#, и постарался сделать его более доходчивым и читаемым:
public static GF_Poly CalcLocatorPoly(GF_Poly Syndromes, uint NumOfErCorrSymbs) {
//Алгоритм Берлекэмпа-Мэсси
GF_Poly Locator;
GF_Poly Locator_old;
//Присваиваем локатору инициализирующее значение (1*X^0)
Locator = new GF_Poly(new byte[] { 1 });
Locator_old = new GF_Poly(Locator);
uint Synd_Shift = 0;
for (uint i = 0; i < NumOfErCorrSymbs; i++) {
uint K = i + Synd_Shift;
GF_Byte Delta = Syndromes[K];
for (uint j = 1; j < Locator.Len; j++) {
Delta += Locator[j] * Syndromes[K - j];
}
//Умножение полинома на икс (эквивалентно сдвигу вправо на 1 байт)
Locator_old = Locator_old.MultiplyByXPower(1);
if (Delta.val != 0) {
if (Locator_old.Len > Locator.Len) {
GF_Poly Locator_new = Locator_old.Scale(Delta);
Locator_old = Locator.Scale(Delta.Inverse());
Locator = Locator_new;
}
//Scale – умножение на константу. Можно было бы
//вместо использования Scale
//умножить на полином нулевой степени. Разницы нет, но так короче:
Locator += Locator_old.Scale(Delta);
}
}
return Locator;
}Пояснения по коду
Класс GF_Poly по сути – обёртка над массивом GF_Byte. Есть ещё одна особенность. Свойство Lenght любого массива — возвращает количество его элементов независимо от значений элементов. Здесь Len — возвращает количество членов полинома. Массив может быть любой длины, но если начиная с какого-то номера все элементы равны нулю, то старшая степень полинома — это последний ненулевой элемент.
Приведённый алгоритм считает локатор. Если количество «ошибок» больше, чем количество избыточных символов, поделённое на 2, то алгоритм не сработает правильно.
Если в сообщении, которое мы используем для примера –
DB 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 43,
ошибиться в нулевом и последнем символе (2 «ошибки», мы притворяемся, что не знаем в каких позициях ошиблись), получится такой полином:
02 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 01,
Полином синдромов для него 4B A7 E8 BD. Если выполнить функцию, приведённую выше с параметрами 4B A7 E8 BD, и 4 (количество избыточных символов), то она вернёт нам такой полином: 01 12 13. Это не похоже на позиции ошибок, которые мы ожидаем, но полином-локатор содержит в себе информацию о позициях ошибок, ведь это «полином, корнями которого являются числа обратные примитивному члену в степени позиции ошибки». Из этого, если немного поскрипеть мозгами или ручкой по бумаге следует, что позиция ошибки – это логарифм числа по основанию примитивного члена, обратного корню полинома.
E – позиция ошибки, a – примитивный член (2, как правило), R – корень полинома.
Что-ж, будем искать корни в поле. Поиск корней полинома в поле Галуа занятие лёгкое и непыльное. В GF[256] может быть 256 чисел всего, так что иксу негде разгуляться. Просто считаем полином 256 раз, подставляя вместо x число, и если полином посчитался как нуль, то записываем к массиву с корнями текущее значение x. Дальше считаем по формуле и получаем позиции ошибок 00 и 0E, именно там где они и были допущены. Теперь эти значения вместе с синдромами и цифрой 4 можно скармливать алгоритму Форни, чтобы он исправил «ошибки» также, как он исправлял «опечатки».
Ещё пара пояснений
-
Существуют более эффективные алгоритмы поиска корней полинома в поле Галуа. Перебор просто самый наглядный.
-
В позиции 00 в текущем примере находится избыточный символ. Алгоритмам Берлекэмпа-Месси и Форни это абсолютно неважно.
Если у нас есть 4 избыточных символа, при этом мы знаем что есть 2 «опечатки» в известных позициях, то алгоритм Берлекэмпа-Мэсси сможет найти ещё одну «ошибку». Но для этого его нужно будет совсем немного модифицировать. Всего то надо там где мы писали
//Присваиваем локатору инициализирующее значение (1*X^0)
Locator = new GF_Poly(new byte[] { 1 });нужно локатор инициализировать не единичным полиномом, а полиномом-локатором, рассчитанным из известных позиций ошибок. И ещё изменить пару строчек. Весь код, напомню, есть на гитхабе.
Надеюсь материал в этой статье поможет тем, кто захочет в каком-нибудь своём проекте реализовать избыточное кодирование без сторонних библиотек. Просьба: Если что-то не понятно, не стесняйтесь комментировать. Постараюсь ответить на вопросы, или внести правки в статью.
4.9.1. Вероятность символьной ошибки для модуляции MPSK
4.9.2. Вероятность символьной ошибки для модуляции MFSK
4.9.3. Зависимость вероятности битовой ошибки от вероятности символьной ошибки для ортогональных сигналов
4.9.4. Зависимость вероятности битовой ошибки от вероятности символьной ошибки для многофазных сигналов
4.9.5. Влияние межсимвольной интерференции
4.9.1. Вероятность символьной ошибки для модуляции MPSK
Для больших отношений сигнал/шум вероятность символьной ошибки для равновероятных сигналов в M-арной модуляции PSK с когерентным обнаружением можно выразить как [7]
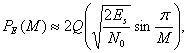
где — вероятность символьной ошибки,
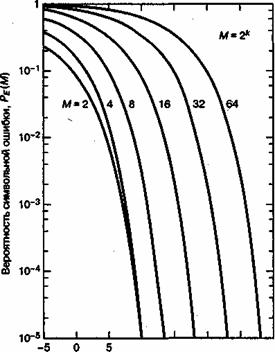
— энергия, приходящаяся на символ, а М = 2k — размер множества символов. Зависимость
от
для передачи сигналов MPSK с когерентным обнаружением показана на рис. 4.35.
Рис. 4.35. Вероятность символьной ошибки для многофазной передачи сигналов с когерентным обнаружением. (Перепечатано с разрешения авторов из W. С. Lindsey and M. К. Simon. Telecommunication Systems Engineering. Prentice-Hall, Inc., Engle-wood Cliffs, N. J., 1973.)
Вероятность символьной ошибки для дифференциального когерентного обнаружения М-арной схемы DPSK (для больших значений ) выражается подобно тому, как это было приведено выше [7].
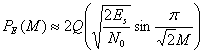
4.9.2. Вероятность символьной ошибки для модуляции MFSK
Вероятность символьной ошибки для равновероятных ортогональных сигналов с когерентным обнаружением можно выразить как [5]
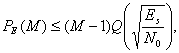
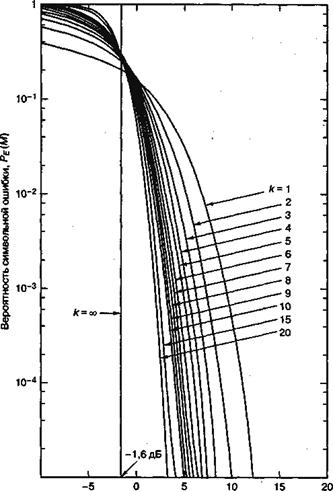
где — энергия, приходящаяся на символ, а M — размер множества символов. Зависимость
от
для М-арных ортогональных сигналов с когерентным обнаружением показана на рис. 4.36.
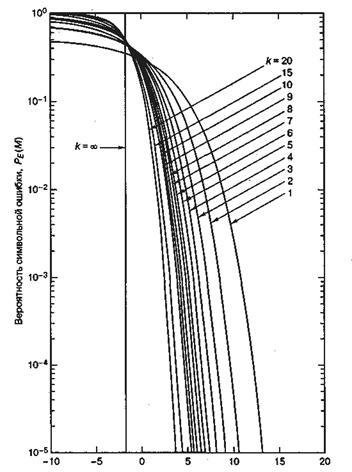
Вероятность символьной ошибки для равновероятных М-арных ортогональных сигналов с некогерентным обнаружением дается следующим выражением [9].
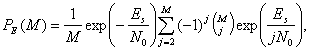
где
(4.109)
является стандартным биномиальным коэффициентом, выражающим число способов выбора j ошибочных символов из М возможных. Отметим, что для бинарного случая формула (4. 108) сокращается до
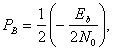
что совпадает с результатом, полученным в выражении (4.96). Кривая зависимости от
для M-арной передачи сигналов с некогерентным обнаружением изображена на рис. 4.37. При сравнении данных графиков с приведенными на рис. 4.6 и соответствующими когерентному обнаружению можно заметить, что для k > 7 различием уже можно пренебрегать. В заключение отметим, что для когерентного и некогерентного приема ортогональных сигналов верхний предел вероятности ошибки дается выражением [9].
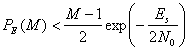
Здесь Es — энергия на символ, а М — размер алфавита символов.
Рис. 4.36. Вероятность символьной ошибки для М-арной ортогональной передачи сигналов с когерентным обнаружением. (Перепечатано с разрешения авторов из W. С. Lindsey and M. К. Simon. Telecommunication Systems Engineering. Prentice-Hall, Inc., Englewood Cliffs, N. J., 1973.)
4.9.3. Зависимость вероятности битовой ошибки от вероятности символьной ошибки для ортогональных сигналов
Можно показать [9], что соотношение между вероятностью битовой ошибки (РВ) и вероятностью символьной ошибки (РЕ) для ортогональных M-арных сигналов дается следующим выражением.
(4.112)
Рис. 4.37. Вероятность символьной ошибки для М-арной ортогональной передачи сигналов с некогерентным обнаружением. (Перепечатано с разрешения авторов из W. С. Lindsey and М. К. Simon, Telecommunication Systems Engineering. Prentice-Hall, Inc., Engtewood Cliffs, N. J., 1973.)
В пределе при увеличении k получаем следующее.
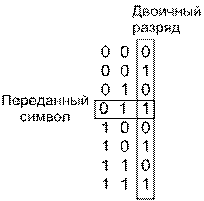
Понять формулу (4.112) позволяет простой пример. На рис. 4.38 показан восьмеричный набор символов сообщения. Эти символы (предполагаемые равновероятными) передаются с помощью ортогональных сигналов, таких как сигналы FSK. При использовании ортогональной передачи ошибка принятия решения равновероятно преобразует верный сигнал в один из (М — 1) неверных. Пример на рисунке демонстрирует передачу символа, состоящего из битов 011. Ошибка с равной вероятностью может перевести данный символ в любой из оставшихся 2k— 1 = 7 символов. Отметим, что наличие ошибки еще не означает, что все биты символа являются ошибочными. Если (рис. 4.38) приемник решит, что переданным символом является нижний из указанных, состоящий из битов 111, два из трех переданных битов будут верными. Должно быть очевидно, что для недвоичной передачи РВвсегда будет меньше РЕ (РB и РЕ — средние частоты появления ошибок).
Рис. 4.38. Пример зависимости рв от ре
Рассмотрим любой из столбцов битов на рис. 4.38. Каждая битовая позиция на 50% заполнена нулями и на 50% — единицами. Рассмотрим первый бит переданного символа (правый столбец). Сколько существует возможностей появления ошибочного бита 1? Всего существует 2k— 1 =4 возможности (нули в столбце появляются в четырех местах) появления битовой ошибки; то же значение получаем для каждого столбца. Окончательное соотношение рв/ре Для ортогональной передачи сигналов в формуле (4.112) получается следующим образом: число возможностей появления битовой ошибки (2k-1) делится на число возможностей появления символьной ошибки (2k— 1). Для случая, изображенного на рис. 4.38, .
4.9.4. Зависимость вероятности битовой ошибки от вероятности символьной ошибки для многофазных сигналов
При передаче сигналов MPSK значение РВменьше или равно РЕ, так же как и при передаче сигналов MFSK. В то же время имеется и существенное отличие. Для ортогональной передачи сигналов выбор одного из (М- 1) ошибочных символов равновероятен. При передаче в модуляции MPSK каждый сигнальный вектор не является равноудаленным от всех остальных. На рис. 4.39, а показано восьмеричное пространство решений, где области решений обозначены 8-ричными символами в двоичной записи. При передаче символа (011) и появлении в нем ошибки наиболее вероятными являются ближайшие соседние символы, (010) и (100). Вероятность превращения символа (011) вследствие ошибки в символ (111) относительно мала. Если биты распределяются по символам согласно двоичной последовательности, показанной на рис. 4.39, а, то некоторые символьные ошибки всегда будут давать две (или более) битовые ошибки, даже при значительном отношении сигнал/шум.
а) б)
Рис. 4.39. Области решения в сигнальном пространстве MPSK: а) в бинарной кодировке; 6) в кодировке Грея
Для неортогональных схем, таких как MPSK, часто используется код преобразования бинарных символов в M-арные, такие, что двоичные последовательности, соответствующие соседним символам (сдвигам фаз), отличаются единственной битовой позицией; таким образом, при появлении ошибки в М-арном символе высока вероятность того, что ошибочным является только один из k прибывших битов. Кодом, обеспечивающим подобное свойство, является код Грея (Gray code) [7]; на рис/4.39, б для восьмеричной схемы PSK показано распределение битов по символам с использованием кода Грея. Можно видеть, что соседние символы отличаются одним двоичным разрядом. Следовательно, вероятность появления многобитовой ошибки при данной символьной ошибке значительно меньше по сравнению с некодированным распределением битов, показанным на рис. 4.39, а. Реализация подобного кода Грея представляет один из редких случаев в цифровой связи, когда определенная выгода может быть получена без сопутствующих недостатков. Код Грея — это просто присвоение, не требующее специальных или дополнительных схем. Можно показать [5], что при использовании кода Грея вероятность ошибки будет следующей.
(4.113)
Напомним из раздела 4.8.4, что передача сигналов BPSK и QPSK имеет одинаковую вероятность битовой ошибки. Формула (4.113) доказывает, что вероятности символьных ошибок этих схем отличаются. Для модуляции BPSK РЕ = РВ, а для QPSK РЕ 2РВ. Точное аналитическое выражение вероятности битовой ошибки РB в восьмеричной схеме PSK, а также довольно точные аппроксимации верхнего и нижнего пределов РB для M-арной PSK при больших М можно найти в работе [10].
4.9.5. Влияние межсимвольной интерференции
Обнаружение сигналов рассматривалось при наличии шума AWGN в предположении, что межсимвольная интерференция (intersymbol interference — ISI) отсутствует. Это упростило анализ, поскольку процесс AWGN с нулевым средним описывается единственным параметром — дисперсией. На практике обычно оказывается, что межсимвольная интерференция — это второй (после теплового шума) источник помех, которому необходимо уделять пристальное внимание. ISI может возникать вследствие использования узкополосных фильтров на выходе передатчика, в канале или на входе приемника. Результатом этой дополнительной интерференции является ухудшение достоверности передачи как для когерентного, так и некогерентного приема. Вычисление вероятности ошибки при ISI (помимо AWGN) является значительно более сложной задачей, поскольку в вычислениях будет фигурировать импульсная характеристика канала. Этот вопрос мы не рассматриваем; впрочем, для читателей, интересующихся данной темой, можно порекомендовать работы [11-16].

80
Любая отдельная ошибка в разряде приведёт к нарушению чётности в одном столбце и в одной из строк матрицы. Прямоугольный код может исправить любую единичную ошибку, поскольку расположение ошибки однозначно определяется пересечением строки и столбца, в которых была нарушена чётность. Вероятность ошибки сообщения для кода, который может исправить ошибочные комбинации, состоящие из t или менее ошибочных битов записывается как
|
n |
n |
)n j . |
|||||||
|
P |
(1 P |
(12.16) |
|||||||
|
P j |
|||||||||
|
M |
ош |
ош |
|||||||
|
j t 1 |
j |
Судить о положительном эффекте от кодирования можно на основе анализа графиков зависимостей вероятности ошибки на бит от отношения сигнал/шум, приведённых на рис. 12.6.
|
Рош |
|||||
|
2 |
1 |
||||
|
10–1 |
|||||
|
3 |
|||||
|
10–2 |
|||||
|
4 |
|||||
|
10–3 |
|||||
|
10–4 |
10 lg(Ec/N0), дБ |
||||
|
–4 |
–2 |
0 |
2 |
||
|
–6 |
кривая 1 – передача сигналами BPSK без помехоустойчивого кодирования; кривые 2–4 – передача сигналами BPSKс помехоустойчивым кодированием со скоростями Vк2 = 1,0; Vк3 = 0,3; Vк4 = 0
Рис. 12.6. Графики зависимостей вероятности ошибки на бит от отношения сигнал/шум для помехоустойчивости пакетов с использованием помехоустойчивых кодов
Анализ показывает, что выигрыш в отношении сигнал/шум при равной Рош на бит может достигать более десяти децибел, что указывает на прямую выгоду от применения.
Рассмотрим выигрыш от применения помехоустойчивого декодирования блоковых кодов при условии, что ошибки в радиоканале при приёме кодовых символов происходят независимо с вероятностью p0. Вероятность появления равно i ошибок в блоке из n символов подчиняется биномиальному закону из (12.13):
|
P |
i |
(1 p |
)n i . |
(12.17) |
||
|
C |
pi |
0 |
||||
|
i |
0 |
|||||
|
n |

81
Если при кодировании исправляются все ошибки кратности t и менее,
n
то вероятность ошибочного приёма кодовой комбинации Pk Pi . При
i t 1
числе ошибок в канале (t+1) и более они возникают случайно и будут в равной степени искажать как информационные, так и проверочные символы. Поэтому среднее значение вероятности ошибки в двоичном символе (бите)
|
n |
i |
1 |
||||
|
P |
P . |
(12.18) |
||||
|
n |
||||||
|
ош |
i t 1 |
i |
При малой вероятности ошибки в канале (p0 << 1), что имеет место на практике, можно ограничиться первым членом ряда и
|
2t 1 |
t 1 |
||||||
|
P |
C |
pt 1. |
|||||
|
ош |
n |
n |
0 |
||||
Вероятность ошибки p0 определяется аналогично вероятности ошибки при приёме сигнала без кодирования, но с учётом скорости используемого кода Vk =k/n. Например, при фазовой модуляции в радиоканале вероятность будет
|
1 |
1 |
(12.19) |
|||||||||
|
2E |
k/N |
n |
|||||||||
|
P |
|||||||||||
|
ош |
2 |
б |
0 |
где Eб – энергия, затрачиваемая на передачу одной двоичной единицы. Наиболее распространёнными типами блочных кодов, применяемых в
системах радиодоступа, являются коды Хэмминга, циклические коды РидаСоломона, редко применяются коды Боуз–Чоудхури–Хоквингема (БЧХ).
Коды Хэмминга имеют структуру
(n,k) = (2m–1, 2m–m–1),
где т = 2,3,… . Минимальное расстояние для кода Хэмминга dmin = 3, поэтому он способен исправлять любую одиночную ошибку или обнаруживать две.
Коды БЧХ относятся к циклическим и имеют структуру
(n,k) = (2m–1, 2m–mt–1),
где т = 3,4,… . Минимальное расстояние dmin 2t+1 позволяет исправлять любые комбинации из t и менее ошибок. Коды БЧХ достаточно разнообразны и допускают при фиксированном значении длины кодовой комбинации n = 2m–1 несколько вариантов исправляющей способности кода. Например, при п = 15 может быть три варианта кода с t = 1,2,3; а при п = 255 – 33 варианта кода с исправляющей способностью t от 1 до 63.
Наиболее часто применяемым в цифровых системах радиодоступа является код Рида–Соломона. Кодом Рида–Соломона называется групповой линейный недвоичный циклический (n,k)-код, построенный над расширенным полем Галуа, исправляющий ошибки кратности t = (n–k)/2. Параметры кода n = m(2m–1), k = m(2m–1)–2mt. Минимальное расстояние
dmin = m(2t+1),
где т – число бит в одном недвоичном символе.

82
Свою популярность коды Рида-Соломона (РС) получили благодаря удобству исправления пакетов ошибок длиной т. На базе классического кода Рида-Соломона формируется большое количество производных: расширенных и укороченных кодов, которые легко адаптируются к конкретной длине сообщения.
На рис. 12.7 приведены графики зависимостей Pош от отношения сиг-
нал/шум h02 для различных типов помехоустойчивых кодов.
Коды Хэмминга (кривые 2,3) обеспечивают выигрыш всего несколько децибел, но при этом являются наиболее простыми в реализации. Наибольший выигрыш в энергетике обеспечивают коды Рида–Соломона (кривые 6,7). Коды БЧХ занимают промежуточное положение.
|
10–2 |
Pош |
|||||
|
1 |
||||||
|
10–3 |
2 |
|||||
|
3 |
||||||
|
10–4 |
||||||
|
6 |
4 |
|||||
|
10–5 |
||||||
|
10–6 |
7 |
5 |
||||
|
4 |
6 |
8 |
10 |
12 |
10 lg h2 |
, дБ |
|
0 |
кривая 1 – сигнал BPSK без кодирования; кривые 2,3 – сигнал BPSK с кодом Хэмминга
(7,4) и (15,11); кривые 4,5 – сигнал BPSK с кодом БЧХ (127,36) и (127,64);
кривые 6,7 – сигнал MFSK (М = 32)с кодом РС n = 31, t = 8 и 4
Рис. 12.7. Зависимость Pош от отношения сигнал/шум h02 для различных типов помехоустойчивых кодов
Перемежение представляет собой эффективный метод борьбы с группирующимися ошибками в канале с замираниями. Идея метода заключается в «рассеянии» символов кодового слова: символы должны находиться друг от друга на таком расстоянии, чтобы быть подверженными независимым замираниям. При независимых замираниях символы, поражённые пакетом ошибок, принадлежат различным кодовым словам. Поэтому влияние пакета ошибок распределяется по всему сообщению, и появляется возможность восстановить данные с помощью исходного кода, исправляющего ошибки.
Известно несколько типов перемежителей, реализующих диагональное, свёрточное, межблоковое и блоковое перемежение. Наиболее простым из четырёх типов перемежителей является блоковый, в котором l кодовых слов исходного кода размещаются в виде l строк прямоугольной матрицы, а их считывание для передачи осуществляется по столбцам, как показано на рис. 12.8. Каждое кодовое слово содержит n символов (k информационных и

83
n–k избыточных символов). Прямоугольная таблица содержит l кодовых слов. Параметр l называется глубиной перемежения. Независимо от начала возникновения пакета ошибок длиной l он будет поражать только один символ каждой строки. Таким образом, если исходный код обладает способностью исправлять одиночные ошибки в пределах кодового слова, то код с перемежением будет исправлять одиночные пакеты ошибок длиной l или менее. Если же исходный код может исправлять одиночные пакеты ошибок длиной t и менее, то код с перемежением будет исправлять одиночные пакеты длиной lt или менее.
l
n–k k
Рис. 12.8. Передача кода с блоковым перемежением
Преимущество свёрточных кодов по отношению к блочным заключается в непрерывном обнаружении и исправлении ошибок. Свёрточный код задаётся тремя параметрами: n, k и K. Код (n, k, K) генерирует n бит выходной последовательности из k входных бит. Для формирования выходной последовательности используется K*k входных бит.
В каждый i-й тактовый момент времени на вход кодирующего устройства поступает (параллельно) k0 символов сообщения, а с выхода снимается n0 символов, соответствующих входным. Выходные символы формируются с помощью рекуррентных соотношений из K информационных символов, поступивших в данный и предшествующие моменты времени. Величина K называется длиной кодового ограничения и играет ту же роль, что и длина блочного кода.
Свёрточный код имеет избыточность R = 1–k0/n0 = 1–Vk, где Vk – скорость кода, и обозначается как (k0/n0). Типичными являются скорости кода
Vk = 1/n0 (например, Vk = 1/2) и Vk = n–1/n (например, Vk = 2/3). При Vk = 2/3 на вход кодирующего устройства одновременно поступают k0 = 2 информационных символа, а снимается n0 = 3 кодовых символа.
Корректирующая способность свёрточного кода зависит от так называемого свободного расстояния, которое по существу содержит ту же информацию о коде, что и кодовое расстояние для блоковых кодов.

84
Свёрточные коды находят применение в системах связи. Для декодирования свёрточного кода при небольших значениях длины кодового ограничения (K = 3, 5, 7) целесообразно использование алгоритма максимального правдоподобия, предложенного А. Витерби. Декодирующее устройство при этом оказывается достаточно простым, реализуя в то же время высокую помехоустойчивость.
Исследования показывают, что применение свёрточных кодов при фиксированной вероятности ошибки p = 10–5 позволяет получить энергетический выигрыш 4…6 дБ по сравнению с системой, использующей фазомодулированные сигналы без кодирования.
На рис. 12.9 приведены графики зависимостей Pош от h02 , позволяющие судить о возможностях свёрточных кодов. В сравнении со случаем без кодирования и использованием сигнала BPSK (кривая 1) выигрыш зависит от схемы принятия решения (жёсткая или мягкая) при приёме, от скорости кодирования Vк и количества блоков K, учитываемых при формировании выходной кодовой комбинации длиной n.
|
10–2 |
Pош |
|||||
|
10–3 |
||||||
|
2 |
1 |
|||||
|
10–4 |
||||||
|
3 |
4 |
|||||
|
10–5 |
||||||
|
10–6 |
||||||
|
2 |
4 |
6 |
8 |
10 10 lg h2 |
, дБ |
|
|
0 |
кривая 1 – сигнал BPSK без кодирования; кривая 2 – Vк = 1/3, К = 41 (жёсткое решение); кривая 3 – Vк = 1/3, К = 7 (мягкое решение); кривая 4 – Vк = 1/2, К = 7 (жёсткое решение)
Рис. 12.9. Зависимость Pош от отношения сигнал/шум h02
Турбокоды (ТК) впервые были введены в 1993 году. С их использованием достигается вероятность появления ошибок 10–5 при скорости кодирования 1/2 и модуляции BPSK в канале с белым аддитивным гауссовым шумом с Eb/N0, равным 0,7 дБ. Коды образуются посредством компоновки двух или более составных кодов, являющихся разными вариантами чередования одной и той же информационной последовательности. Для свёрточных кодов декодер выдаёт жёстко декодированные символы, в каскадной схеме, такой как турбокод, для хорошей работы алгоритм декодирования применяет мягкую схему декодирования, вместо жёсткой. Для систем с турбодекодированием, декодирование заключается в том, чтобы передать мягкую схему при-

85
нятия решений с выхода одного декодера на вход другого и повторять эту процедуру до тех пор, пока не будут получены надёжные решения.
На рис. 12.10 приведены графики зависимостей Pош от h02 , позволяющие оценить эффект от применения турбокодов. В частности, вероятность ошибки Pош = 10–5 достигается при 10 lgh02 = 0,7 дБ (кривая 2). Для сравнения на рис. 12.10 приведён график зависимости Pош от h02 для сигналов BPSK без кодирования.
Pош
10–1
1
10–2
2
10–3
10–4
10–5
|
2,5 |
3 |
4,5 |
6 10 lg h2 |
, дБ |
|
0 |
Рис. 12.10. Зависимость Pош от отношения сигнал/шум h02
Турбокоды являются одним из наиболее мощных средств повышения помехоустойчивости среди методов кодирования.
Компаниями France Telecom и Telediffusionde France запатентован ши-
рокий класс турбокодов. Более того, турбокоды утверждены для помехоустойчивого кодирования несколькими стандартами космической связи, а также мобильной связи третьего поколения.
Схема кодирования с кодерами на 16 состояний (K = 5), максимальной длиной перемежения 16384 и кодовыми скоростями r = 1/2,1/3,1/4,1/6 утвер-
ждена в 1999 г. американским комитетом CCSDS (Consultative Committee for Space Data Systems) в стандарте передачи телеметрической информации с космических аппаратов. В феврале 2000 г. консорциум DVB утвердил ТК в стандарте DVB-RCS для передачи информации по обратному спутниковому каналу (Return Channel for Satellite – RCS), т. е. в направлении от спутника к абоненту. ТК формируются на основе циклического рекурсивного система-
тического свёрточного кодера (Circular Recursive Systematic Convolutional– CRSC). Использование стандарта совместно с вещательным стандартом DVB-S позволяет проектировать полноценную широкополосную систему спутникового интерактивного цифрового телевидения. Компанией TurboConcept в партнёрстве с европейским спутниковым оператором Eutelsat разработан турбо-декодер TC1000 в соответствии со стандартом DVB-RCS.
86
Использование ТК принято также в новом стандарте спутниковой системы связи Inmarsat.
Применение многопозиционной модуляции КАМ и MSPK в чистом виде сопряжено с проблемой недостаточной помехоустойчивости. Поэтому во всех современных высокоскоростных протоколах КАМ используется совместно с решётчатым кодированием – специальным видом свёрточного кодирования. В результате появился новый способ модуляции, называемый треллисмодуляцией (Trellis Coded Modulation – ТСМ). Выбранная определённым образом комбинация конкретной КАМ и помехоустойчивого кода в отечественной технической литературе носит название сигнально-кодовой конструкции (СКК). СКК позволяют повысить помехозащищённость передачи информации наряду со снижением требований к отношению сигнал/шум в канале на 3–6 дБ. При этом число сигнальных точек увеличивается вдвое за счёт добавления к информационным битам одного избыточного, образованного путём свёрточного кодирования. Расширенный таким образом блок битов подвергается всё той же КАМ. В процессе демодуляции производится декодирование принятого сигнала по алгоритму Витерби. Именно этот алгоритм за счёт использования введённой избыточности и знания предыстории процесса приёма позволяет по критерию максимального правдоподобия выбрать из сигнального пространства наиболее достоверную эталонную точку.
Выбор способов модуляции и кодирования сводится к поиску такого заполнения сигнального пространства, при котором обеспечивается высокая скорость и высокая помехоустойчивость. Комбинирование различных ансамблей многопозиционных сигналов и помехоустойчивых кодов порождает множество вариантов сигнальных конструкций. Согласованные определённым образом варианты, обеспечивающие улучшение энергетической и частотной эффективности, и являются сигнально-кодовыми конструкциями. Задача поиска наилучшей СКК является одной из наиболее сложных задач теории связи.
Все применяемые сегодня СКК используют свёрточное кодирование со скоростью (n – 1/n), т. е. при передаче одного сигнального элемента используется только один избыточный двоичный символ.
Типичный кодер, применяемый совместно с модулятором ФМ-8 представлен на рис. 12.11. Он является свёрточным кодером с относительной скоростью кода, равной 2/3. Каждым двум информационным битам на входе кодер сопоставляет трёхсимвольные двоичные блоки на своём выходе, которые и поступают на модулятор ФМ-8.

87
|
элемент задержки |
||
|
на один такт |
||
|
c1 |
||
|
c0 |
||
|
ci |
||
К модулятору ФМ-8
Рис. 12.11. Схема свёрточного 2/3 кодера
Применение сигналов ФМ связано с разрешением проблемы неоднозначности фазы восстановленной на приёме несущей. Данная проблема решается за счёт относительного (дифференциального) кодирования, что в системах без помехоустойчивого кодирования приводит к размножению ошибок. В системах с помехоустойчивым кодированием относительное кодирование также используется. В этом случае имеет значение последовательность включения относительного и помехоустойчивого кодера.
Известно несколько видов СКК, обеспечивающих прозрачность к неопределённости фазы восстановленной несущей. Они также основаны на свёрточном кодировании со скоростью (n–1/n).
Использование методов кодирования совместно с методами модуляции даёт мощный арсенал средств, который способен подобрать оптимальное сочетание кода и вида модуляции, обеспечивающих максимальную эффективность радиолинии.
Для иллюстрации на рис. 12.12 приведены графики зависимостей скорости передачи информации от отношения сигнал/шум на входе приёмника. Анализ приведённых кривых показывает, что при различных отношениях сигнал/шум максимальное значение пропускной способности обеспечивает, например при h02 = 12 дБ, сочетание сигнала QPSK с кодом со скоростью
Vк = 3/4, а при h02 = 16 дБ – сигнала 16QAM и код со скоростью Vк = 1/2.

|
88 |
|||||
|
= V/c |
|||||
|
1 |
4 |
||||
|
0,75 |
|||||
|
3 |
|||||
|
0,5 |
|||||
|
2 |
|||||
|
0,25 |
|||||
|
1 |
10 lg h2 |
, дБ |
|||
|
0 |
0 |
||||
|
12 |
16 |
20 |
24 |
||
|
8 |
кривая 1 – QPSK с кодом Vк = 1/2; кривая 2 – QPSK с кодом Vк = 3/4; кривая 3 – 16QAM
с кодом Vк = 1/2; кривая 4 – 16QAM с кодом Vк = 3/4;
Рис. 12.12. Зависимость эффективности использования пропускной способности канала связи от вида кодирования и способа модуляции
Поэтому в современных системах радиодоступа реализован режим адаптации вида модуляции и способа кодирования с целью максимизации пропускной способности индивидуально для каждой БС и (если это возможно) для каждой АС.

89
Лекция 13 ИНФОРМАЦИОННЫЕ ХАРАКТЕРИСТИКИ КАНАЛОВ СВЯЗИ
Основными информационными характеристиками каналов связи являются скорость передачи информации и пропускная способность каналов связи.
Скорость передачи информации вводится как количество информации, получаемое на выходе канала связи в единицу времени
V VM (H(X ) H(X /Y));
при отсутствии помех
V VM H (X ).
Мы всегда стремимся максимизировать скорость передачи информа-
ции V max.
Рассмотрим для примера задачу Шеннона.
|
p(x ) p(x |
) |
1 |
; p + q = 1; q |
p |
– матрица переходов; |
|||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||
|
1 |
2 |
|||||||||||||||||||||||||||||||||
|
p |
q |
|||||||||||||||||||||||||||||||||
|
I(X,Y) H(X) H(X /Y); |
||||||||||||||||||||||||||||||||||
|
1 |
1 |
1 |
1 |
log2 1. |
||||||||||||||||||||||||||||||
|
H(X) |
log |
log |
||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||
|
2 |
2 |
2 |
||||||||||||||||||||||||||||||||
|
Потерянная информация: |
||||||||||||||||||||||||||||||||||
|
H(X /Y) |
1 |
(plog p plogq) |
1 |
(qlog q qlog p) plog |
1 |
qlog |
1 |
, |
||||||||||||||||||||||||||
|
2 |
2 |
p |
q |
|||||||||||||||||||||||||||||||
|
откуда (рис. 13.1): |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||||||||
|
IY |
(X) 1 plog |
qlog |
1 (1 q)log |
qlog |
, |
|||||||||||||||||||||||||||||
|
тогда получим: |
p |
q |
1 q |
q |
||||||||||||||||||||||||||||||
|
1 |
1 |
|||||||||||||||||||||||||||||||||
|
V |
V |
1 plog |
qlog |
. |
||||||||||||||||||||||||||||||
|
и |
M |
p |
q |
|||||||||||||||||||||||||||||||
IY(X)
1
Рис. 13.1. Зависимость переданной информации от вероятности ошибки
.
Максимальное количество переданной информации, взятое по всевозможным источникам с распределением сигналов p(xi) называется пропускной
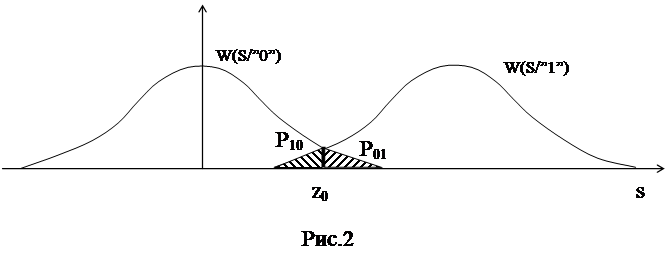
Вероятности
ошибок зависят от отношения сигнал/шум q, а также
от величины порога z0. Для равновероятного источника порог
выставляется симметрично, таким образом, чтобы добиться равных вероятностей
перепутывания . В таком случае вероятность
ошибки равна просто вероятности перепутывания символов .
В
системе с амплитудной модуляцией вероятность ошибки равна
Данная
величина ошибки достигается для равновероятного источника при оптимальной
величине порога z0=Э/2.
 |
При
моделировании системы передачи информации производится экспериментальное
определение вероятности ошибки. По классическому определению вероятностью
события А называется отношение количество экспериментов, в которых событие А
произошло, к общему количеству экспериментов
В
нашем случае отношение ошибочно переданных символов к общему количеству принятых
символов.
При
конечном количестве экспериментов N<¥ мы имеем дело с
оценкой вероятности. При этом оцененная величина вероятности ошибки сама
является случайной величиной. Для уменьшения ошибки измерения необходимо
увеличивать объём эксперимента. Количество испытаний зависит от порядка
вероятности, которую необходимо измерить, и от допустимой величины погрешности:
где
— допустимая погрешность, P –оцениваемая
вероятность. Очевидно, что чем меньшего порядка вероятность мы хотим измерить,
и с чем большей точностью, тем больше необходимый объём эксперимента.
Описание пакета «Математика», и используемых
подпрограмм
Пакет «Математика» является мощным комплексом
для проведения инженерных и научных вычислений. Программирование в
«Математике» осуществляется на Си – подобном языке. Всё поле
программы поделено на ячейки, каждая из которых ограничена скобкой справа.
Запуск ячейки на выполнение производится нажатием клавиш Shift+Enter. Основными
объектами на рабочем поле являются а) текст программы б) результат вычислений в) графики, рисунки, диаграммы и пр.
Система передачи информации смоделирована с помощью набора
подпрограмм, каждая из которых реализует то или иное преобразование сигнала:
1. datasource[ ]
– генератор бинарного равновероятного сообщения длиной 60 бит, длительность
одной информационной посылки 1мсек;
2. modulatorAM[u,f]
– генератор амплитудно – манипулированного сигнала амплитудой 1 вольт, u
– модулирующее сообщение, f – несущая частота, может принимать значения
от 1 до 40 кГц.
3. noise[s,q]
– канал передачи, осуществляет зашумление сигнала s аддитивным
гауссовским шумом, с отношением сигнал/шум равным q на выходе канала;
4. optimfilter[s,f]
–блок оптимальной фильтрации, реализует оптимальный фильтр, согласованный с
сигналом s по форме, и настроенный на частоту f;
5. detector[s]
– амплитудный детектор сигнала s;
6. threshold[s,z]
– пороговое устройство, сравнивает сигнал s с порогом z;
7. signalview[s,t1,t2]
– оператор просмотра сигнала s на промежутке времени от момента t1
до момента t2 миллисекунд;
8. dataview[u,n1,n2] – оператор просмотра бинарного сообщения u от бита n1 до бита n2.
Любая строка в пакете «Математика» должна
заканчиваться точкой с запятой, в противном случае на экран выводится результат
вычисления.
Домашнее задание:
1. определить
необходимый объём эксперимента для измерения вероятности ошибки в пределах 0.1
до 0.9 с погрешностью не более 5%.
2. определить
оптимальную величину порога для равновероятного источника
Лабораторное задание
1. Запустить
программу «Математика» и реализовать когерентную СПИ с помощью
имеющихся подпрограмм.
2. Пронаблюдать и
зарисовать сигнал во всех точках системы передачи информации: а) на выходе источника сообщения б) на выходе модулятора или
на выходе канала в) после согласованного
фильтра при отношении сигнал/шум q=100.
3. Измерить
зависимость вероятности ошибки от величины отношения сигнал/шум при а) оптимальном пороге б) пороге больше оптимального в) пороге ниже оптимального
4. Исследовать
величину ошибки при оптимальном пороге и частотной расстройке согласованного
фильтра.
5. Выполнить пункты
1-5 для некогерентной системы
Контрольные вопросы:
1. Структура и
принцип работы системы передачи информации с амплитудной модуляцией
2. Критерии выбора
оптимального порога z0
3. Основное отличие
когерентной системы передачи информации от некогерентной.
4. От чего зависит вероятность
ошибки в системе, каким образом можно её уменьшить.
5. От чего зависит
точность измерения случайных величин при моделировании СПИ.
6. В каких случаях
возникает необходимость в применении некогерентной системы обработки сигнала.