Вероятность ошибки после декодирования - Не ошибается лишь тот, кто ничего не делает!

Помехоустойчивость
кода можно оценить вероятностью искажения
(ошибки) символов дискретных сообщений,
которые передаются кодовыми комбинациями.
Выше отмечалось, что по мере увеличения
избыточности кода его помехоустойчивость
улучшается. Однако реальная
помехоустойчивость кодов с избыточностью
зависит и от конкретного способа приема
(регистрации) кодовых комбинаций
(символов). Применяется поэлементный
прием и прием в целом кодовых комбинаций.

При поэлементном
приеме осуществляется регистрация
каждого из символов, составляющих
кодовую комбинацию. Последовательность
поочередно принятых сигналов образует
кодовую комбинацию, которая регистрируется
декодером и подается на устройство
преобразования кодовых комбинаций в
символы сообщения.

При приеме в целом
производится регистрация кодовых
сигналов. Под кодовым
сигналом
при этом
принимается вся последовательность
элементарных сигналов, составляющих
кодовую комбинацию.

Предположим, что
вероятность искажения отдельного
сигнала в кодовой комбинации равна
.
Будем полагать, что искажения различных
сигналов в кодовой комбинации статистически
независимые (что является справедливым
для каналов с постоянными параметрами
и флуктуационной помехой). Вероятность
того, что при поэлементном приеме
комбинация изn
элементов содержит равно

ошибок по
биномиальному закону, равна

,
(8.37)

где

— вероятность
искажения одного элемента кодовой
комбинации.

Вероятность
правильной регистрации кодовой комбинации
из n
элементов равна вероятности того, что
в ней содержится не более

ошибок

.

(8.38)

Число ошибок

и менее
исправляется кодом c
.

Тогда вероятность
ошибочного декодирования кодовой
комбинации

.
(8.39)

При оценке
эффективности помехоустойчивых кодов
используют так называемую эквивалентную
вероятность ошибки
,
определяемую по формуле

,
(8.40)

где
— количество информационных разрядов.

Эквивалентная
вероятность ошибки определяет вероятность
ошибки элементарного символа в двоичном
симметричном канале без памяти, в котором
система с примитивным кодированием
обеспечивает при передаче того же
количества информации ту же вероятность
ошибочного декодирования кодовой
комбинации, что и система с избыточным
кодом.

8.5. Блочные линейные коды

8.5.1. Математическое описание процессов кодирования и декодирования

Линейным блочным
— кодом называется множествопоследовательностей длинынад,
называемых кодовыми словами, которое
характеризуется тем, что сумма двух
кодовых слов является кодовым словом,
а произведение любого кодового слова
на элемент поля также является кодовым
словом.

Поле
,
состоящее из конечного числа элементовназываетсяконечным
полем
или полем
Галуа. Для
любого числа
,
являющегося степенью простого числа,
существует поле, насчитывающееэлементов. Поле не может содержать менее
двух элементов. Поле, включающее только
0 и 1, обозначим GF(2). Правила сложения и
умножения в поле с двумя элементами
представлены в табл. 8.11.

Таблица 8.11. Правила
сложения и умножения в поле с двумя
элементами

+	0	1		х	0	1
0	0	1	0	0	0
1	1	0	1	0	1

Двоичные кодовые
комбинации, являющиеся упорядоченными
последовательностями из
элементов поля,
рассматриваются в теории кодирования
как частный случай последовательностей
изn
элементов поля
.

Обычно
,
где— некоторое целое число. Если,
линейные коды называются групповыми,
так как кодовые слова образуют
математическую структуру, называемую
группой. При формировании этого кода
линейной операцией является суммирование
по mod2.

При задании кода
обычно указывают, какие информационные
элементы принимают участие в формировании
каждого из k
проверочных разрядов. Например, для
кода с n=5,
m=3
и k=2
каждый проверочный разряд
определяется суммированием по модулю
2 по правилу

;

где
— информационные разряды. Комбинация
такого кода записывается в видеили в обратном.
При задании кода можно указать все
разрешенные для этого кода комбинации.
Для линейных кодов способ задания можно
значительно упростить. Дляm
информационных разрядов число всех
разрешенных кодовых комбинаций будет
равняться
.

Пусть
(табл.8.12). Так как в каждой кодовой
комбинации такого кода три информационных
элемента, то число возможных комбинаций
кода будет равно.

Проверочные
элементы формируются как сумма по модулю
два информационных элементов, а именно:

(8.41)

Так для кодовой
комбинации №4

в соответствии с
правилами суммирования по модулю 2.

Для задания кода
нет необходимости записывать в таблицу
все используемые комбинации данного
кода. Код может быть задан матрицей,
которая содержит один из возможных
наборов линейно независимых строк. Под
линейно независимыми кодовыми комбинациями
понимают такие, сумма по модулю 2 которых
(в любом сочетании) не равняется нулю.
Выберем из всех кодовых комбинаций
только линейно независимые. Так для
приведенного выше кода линейно
независимыми будут группы комбинаций:

1. 1 0 0 1 0

2. 0 1 0 1 1

3.
0 0 1 0 1

1. 1 0 0 1 0

4. 1 1 0 0 1

5.
0 1 1 1 0

1. 1 0 0 1 0

4. 1 1 0 0 1

7.
1 1 1 0 0

(1)

(2)

(3)

Можно выбрать и
другие группы линейно независимых
комбинаций этого кода. Путем поэлементного
сложения по модулю 2 любого сочетания
из приведенных выше в группах комбинаций
не удается получить нулевой комбинации.
Для первой группы:

1. 1
0 0 1 0



2.
0
1 0 1 1

———————

1
1 0 0 1

1. 1
0 0 1 0



3.
0
0 1 0 1

——————

1
0 1 1 1

2. 0
1 0 1 1



3.
0
0 1 0 1

———————

0
1 1 1 0

1. 1
0 0 1 0



2.
0
1 0 1 1



3.
0
0 1 0 1

————-

1
1 1 0 0.

Обычно линейно
независимые кодовые комбинации записывают
в виде матрицы размером
,
которая называетсяпорождающей
и обозначается
.
Чаще всего порождающие матрицы записывают
в так называемойканоничной
форме. При
этом первые или последние
столбцов этой матрицы образуютединичную
матрицу.

Таким образом,
любая из трех приведенных выше комбинаций
может быть порождающей для систематического
(5,3) кода с
.
В общем виде производящую матрицу из
строк истолбцов записывают так:

.
(8.42)

Здесь первые
столбцов являются информационными, а
последниестолбцов – проверочными. Производящую
матрицуобычно записывают в канонической форме

или
. (8.43)

где

– число
проверочных элементов,
— матрица информационных элементов,
представляет собой единичную матрицу
размерности,
т.е. квадратная матрица, у которой единицы
находятся только на главной диагонали,— матрица проверочных элементов,
размерность которой.

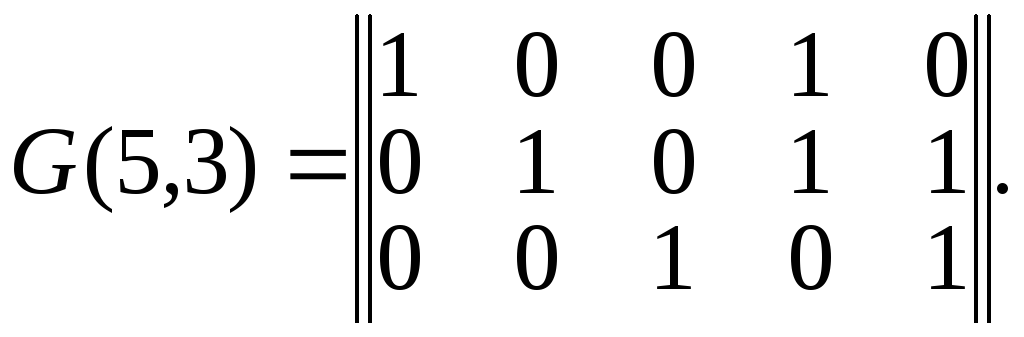
Для рассматриваемого
примера – (5,3) кода каноническая форма
порождающей матрицы имеет вид

Из данного примера
видно, что первые три столбца составляют
единичную матрицу; четвертый столбец
указывает, что при формировании первого
проверочного разряда принимают участие
первый и второй информационные разряды.
Пятый столбец указывает, что при
формировании второго проверочного
разряда принимают участие второй и
третий информационные разряды.

Для

.
(8.44)

Затем выделяется
подматрица
являющаяся транспонированной матрицей:

если
то.
(8.45)

Затем полученной
матрице
справа приписывается единичная матрица
и получается проверочная матрицаН.

.
(8.46)

Проверочная матрица
очень удобна для определения места
ошибки в кодовой комбинации, а следовательно
и исправления ошибки.

Проверочная матрица
однозначно связана с порождающей
соотношением

,
(8.47)

Где умножение и
суммирование соответствующих элементов
матриц производится по модулю 2.

Пример.

Для порождающей
матрицы, G(5,3)
проверочная матрица имеет вид

Тогда

Допустим, что
переданная кодовая комбинация записана
в виде вектора

(8.48)

Процесс декодирования
математически описывают произведением
проверочной матрицы
и вектора – столбца, отображающего
принятую кодовую комбинацию,
где— вектор ошибки

,
(8.49)

где
– результат декодирования (синдром);

— знак транспортирования.

В теории кодирования
синдром, который также называют
опознавателем ошибки, обозначает
совокупность признаков, характерных
для определённой ошибки. Для исправления
ошибки на стороне приёма необходимо
знать не только факт её существования,
но и её местонахождение, которое
определяется по установленному виду
вектора ошибки.

Поскольку связь
между порождающей и проверочной
матрицами, определяется равенством
,
то получим

.
(8.50)

Если обозначить
-й
столбец проверочной матрицы, то

Вектор ошибки
содержит «1» на тех позициях, символы
на которых искажены. Пусть эти позиции
имеют номера,
тогда будет справедливо равенство

.
(8.51)

Следовательно,
если необходимо обнаружить
ошибок, то должно быть выполнено условие

при любом сочетании
искаженных символов.

Если же необходимо
исправить
ошибок, то сумма по модулю 2 для любогоконкретных столбцов проверочной матрицы
должна быть вполне определенной, которая
не совпадает с аналогичной суммой для
другихстолбцов. Так, например, при исправлении
одиночной ошибки все столбцы проверочной
матрицы должны быть разными, то естьпри любыхи;.
Если же необходимо исправить одиночную
ошибку и обнаружить пакет, состоящий
из трех или двух ошибок, то необходимо
выполнить следующие условия:

при
(для исправления одиночной ошибки);

при любых
и(для обнаружения пакета из двух ошибок);

при любых
и(для обнаружения пакета из трех ошибок).

Матрицы
иможно поменять ролями. Тогда матрицабудет порождающей, а— проверочной.

Коды, взаимосвязанные
между собой таким образом, называют
дуэльными (двойственными).

Соседние файлы в папке Пособие ТЕЗ_рус12

Источник

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Ваш е-мэйл

Заполните, если хотите получить ответ

Оцените наш проект

Источник

Ч КОДИРОВАНИЕ И ПЕРЕДАЧА ИНФОРМАЦИИ

удк 621.391 Научные статьи

doi:10.31799/1684-8853-2021-4-71-85 Articles

Вычисление аддитивной границы вероятности ошибки декодирования с использованием характеристических функций

А. Н. Трофимова, канд. техн. наук, доцент, orcid.org/0000-0003-1233-5222, andrei.trofimov@k36.org Ф. А. Таубина, доктор техн. наук, профессор, orcid.org/0000-0002-8781-9531 аСанкт-Петербургский государственный университет аэрокосмического приборостроения, Б. Морская ул., 67, Санкт-Петербург, 190000, РФ

Введение: точное значение вероятности ошибки декодирования обычно не удается вычислить, поэтому стандартный подход при получении верхней границы вероятности ошибки декодирования по максимуму правдоподобия базируется на использовании аддитивной границы и границы Чернова и (или) ее модификаций. Для многих ситуаций этот подход не обеспечивает достаточной точности. Цель: разработка метода точного вычисления аддитивной границы вероятности ошибочного декодирования для широкого класса кодов и моделей каналов без памяти. Методы: использование характеристических функций логарифма отношения правдоподобия для произвольной пары кодовых слов, решетчатого представления кодов и численного интегрирования. Результаты: полученная точная аддитивная граница вероятности ошибочного декодирования основана на сочетании использования характеристических функций и произведения решетчатых диаграмм для рассматриваемого кода, благодаря чему можно получить итоговое выражение в интегральной форме, удобной для численного интегрирования. Важной особенностью предложенной процедуры является то, что она позволяет точно вычислить аддитивную границу с помощью подхода, основанного на использовании передаточных (производящих) функций. При таком подходе метки ветвей в произведении решетчатых диаграмм для рассматриваемого кода заменяются соответствующими характеристическими функциями. Полученное итоговое выражение позволяет с использованием стандартных методов численного интегрирования вычислять значения аддитивной границы вероятности ошибочного декодирования с требуемой точностью. Практическая значимость: по итогам проведенной работы можно заметно улучшить качество оценивания вероятности ошибочного декодирования и тем самым повысить эффективность решений, связанных с применением конкретных схем кодирования для широкого класса каналов связи.

Ключевые слова — декодирование по максимуму правдоподобия, аддитивная граница вероятности ошибки, попарная вероятность ошибки, характеристическая функция, канал с ID-AGN-шумом, канал с аддитивным лапласовым шумом.

Для цитирования: Трофимов А. Н., Таубин Ф. А. Вычисление аддитивной границы вероятности ошибки декодирования с использованием характеристических функций. Информационно-управляющие системы, 2021, № 4, с. 71-85. doi:10.31799/1684-8853-2021-4-71-85

For citation: Trofimov A. N., Taubin F. A. Evaluation of the union bound for the decoding error probability using characteristic functions. Informatsionno-upravliaiushchie sistemy [Information and Control Systems], 2021, no. 4, pp. 71-85 (In Russian). doi:10. 31799/1684-8853-2021-4-71-85

Введение

Широкое использование кодов с исправлением ошибок для хранения, обработки и передачи данных диктует интерес к разработке новых, более точных методов оценки вероятности ошибки, достигаемой при введении помехоустойчивого кодирования. Эффективный метод вычисления вероятности ошибки декодирования может значительно снизить затраты, связанные с анализом и реализацией процедуры кодирования, как за счет рационального выбора параметров схемы кодирования, так и благодаря тому, что не требуется прибегать к компьютерному моделированию.

Поскольку точное значение вероятности ошибки декодирования обычно не удается вычислить, стандартный подход при получении верхней границы вероятности ошибки как для декодирования по максимуму правдоподобия (МП), так и для декодирования по максимуму апостериорной

вероятности (MAB) базируется на использовании аддитивной границы [1, 2]. Хотя эти процедуры декодирования, как правило, являются чрезмерно сложными для длинных кодов, получение подобного рода верхних границ для вероятности ошибки декодирования представляет интерес для коротких и умеренно длинных кодов. При использовании аддитивной границы точная вероятность ошибки декодирования ограничивается сверху суммой попарных вероятностей. Попарная вероятность ошибки представляет собой вероятность такого события для пары кодовых слов, при котором значение правдоподобия (или апостериорная вероятность) для правильного (переданного) кодового слова меньше, чем для неправильного кодового слова. Для канала без памяти и двоичного кода эта вероятность представляет собой вероятность того, что сумма некоторых случайных величин превосходит определенный порог. В ряде ситуаций аддитивная граница позволяет достаточно

точно оценить истинное значение вероятности ошибочного декодирования.

Наряду с аддитивной границей, для оценки вероятности ошибки декодирования могут быть использованы и другие, более точные верхние границы (см., например, обзор [3]), которые обычно подразделяют на две категории (хотя между ними существует весьма тесная связь). К первой категории относятся граница Галлагера — Фано и ее вариации, такие как граница Думана — Салехи (Duman — Salehi bound) и граница Шульмана — Федера (Shulman — Feder bound), а ко второй — так называемые тангенциальные границы (tangential bounds), восходящие к тангенциальной границе Берлекемпа и включающие, в частности, тангенциальную сферическую границу (tangential-sphere bound — TSB) Полтырева, границу Дивсалара (Divsalar bound) и границу Энгдаля — Зигангирова (Engdahl — Zigangirov bound) для сверточных кодов. Однако сфера применения указанных границ довольно ограничена, что связано со следующими факторами. Во-первых, улучшенные верхние границы получены, как правило, для простейших моделей канала (в частности, для канала с аддитивным белым гауссовым шумом) и частных вариантов сигнальных созвездий. Во-вторых, для коротких и умеренно длинных кодов (длиной до 100) улучшенные верхние границы практически совпадают с аддитивной границей при вероятности ошибки декодирования порядка 10-6 и меньше. Заметный же выигрыш в точности наблюдается для турбокодов (с большой величиной перемежения) и длинных низкоплотностных кодов, имеющих достаточно большую сложность декодирования. И, наконец, вычисление улучшенных верхних границ оказывается существенно более сложным, чем аддитивной границы. Поэтому аддитивная граница остается доминирующим инструментом, особенно в плане прикладных исследований для практически значимых моделей каналов, при анализе помехоустойчивости конкретных кодовых схем на основе коротких и умеренно длинных кодов.

Для произвольных кодов и каналов без памяти вычисление как попарных вероятностей, так и аддитивной границы в целом оказывается весьма сложным, поэтому обычно используется следующий подход. Попарная вероятность вначале оценивается сверху с использованием границы Чернова, позволяющей представить ее в виде произведения ряда сомножителей, а затем с помощью передаточной (производящей) функции кода учитываются и суммируются все возможные попарные вероятности, обеспечивая окончательный результат для аддитивной границы в замкнутой форме. Некоторые результаты по уточнению границы Чернова для ряда моделей каналов без памяти можно найти в работе [4].

Точное вычисление попарных вероятностей в замкнутой форме возможно только для относительно простых моделей каналов без памяти. Среди известных подходов к получению в замкнутой форме выражений для попарных вероятностей [5-9] следует выделить подход, предложенный в работе W. Turin: Union Bound on Viterbi Algorithm Performance, AT&T Tech. Journal, 1985, основанный на использовании аппарата характеристических функций. Модификация этого подхода с ориентацией на произвольные модели каналов без памяти и использование компьютерных методов, таких как квадратурные формулы Гаусса — Чебышева и численное интегрирование, оказывается более предпочтительным подходом по сравнению с подходами, основанными на получении аппроксимации аддитивной границы в замкнутой форме.

Также важно, что численное интегрирование, а также квадратурные формулы Гаусса — Чебышева могут применяться для вычисления аддитивной границы, даже если передаточная функция не задана аналитически.

В данной работе предоставлен метод точного вычисления аддитивной границы вероятности ошибочного декодирования для широкого класса кодов и произвольных моделей каналов без памяти. Предложенный метод включает получение точного выражения для попарной вероятности, используемой при получении аддитивной границы. Получение точного выражения для попарной вероятности достигается благодаря использованию характеристических функций (х.ф.) логарифма отношения правдоподобия для рассматриваемой пары кодовых слов.

Представление аддитивной границы с использованием характеристических функций

Решение при декодировании некоторого кода по МП принимается по правилу x = argmaxxPy|x(y|x), где pyx(y| x) — условная вероятность (для канала с дискретным выходом), или n-мерная условная функция плотности вероятности (ф.п.в.), задающая распределение выходных значений y = (y(1), …, y(n)) канала с непрерывным выходом; x — переданное кодовое слово длиной n. Для канала без памяти

Рух(У 1 x) = UPyMl)l ^ (1)

1=1

где pyx(y | x) — одномерная условная вероятность или условная ф.п.в. для канала с дискретным и непрерывным выходом соответственно. Вероятность ошибки при передаче слова x может быть

ограничена сверху с использованием аддитивного неравенства как

Ре (X) Ре (X ^ X’ | X), (2)

где

Ре (X ^ X’ | X) = РГ [р(у | X’) > р(у | X) | X] (3)

— вероятность ошибки декодирования для кода из двух слов x и x’ при условии, что было передано слово x, а суммирование по x’ здесь и далее понимается как суммирование по словам кода. Вероятность (3) с использованием равенства (1) может быть записана в эквивалентной форме Pe(x ^ ^ | x) = Рг[£(у | x, x’) > 0 | x], где я(у|X, X’) = ХГ=!^(у(г)|х(1), х'{1)) и

г(у | х, х’) = 1п

Ру|х(У| х>) Рух(У | х)’

(4)

Вычисление аддитивной границы для вероятности ошибки декодирования pe базируется на использовании следующего результата [10]:

«Утверждение. Пусть Z — вещественная случайная величина и wZ(•) — ее ф.п.в. Пусть С(ю) — х.ф. случайной величины Z, т. е.

Ся (ю) = е]юЯ = | е]юЯшя (х)ах,

(5)

черта сверху здесь и далее обозначает усреднение. Тогда

1 к

Рг[Я > 0] = — [ Ив

77″

Сг (д-/Р) Р+]’а

da, 0< р < р0,

где р0 — максимальное значение 1тю, при котором сходится интеграл (5), который может быть записан в виде

Ся И ю=а-]р = Ся (а — ]’р) =

= е]'(а-]’р)я = | е]ахерхшя (x)dx =

—к

к к

= | ерх сов(ах)шг (x)dx + ] | ерх В1п(ах)шг (x)dx. (6)

Заметим, что обычно х.ф. определяется как функция вещественного аргумента, но здесь рассмотрено ее обобщение как функции комплексного аргумента ю.

Используя это утверждение, а также то обстоятельство, что канал описывается моделью без памяти [см. (1)], можно записать, что

П с, (а-]’р; х(1), х'(1))

Ре (X ^ X’ | X) = — [ Ив

ТТ <1

р + ]а

^а

при 0< р < р0,

где

(ю; х, х’) = вхр( ]’юг(у | х, х’))

с, (ю;

(7)

(8)

— х.ф. случайной величины z(y | x, x’), определенной равенством (4), а верхняя граница р0 следует из условия сходимости интеграла (6).

Вероятность ошибки декодирования pe оценивается сверху с использованием аддитивного неравенства (2)

Ре Ре (X ^ X’ | X)P(X) =

П с, (а-/р; х(1), х'(1))

1 ■ ■

-1 I [ Кв^

лМ

X X ^ 0

р + ]а

-da =

1 к ХХШ (а-/р; х(1), х'(1))

— [ Е^^-^, (9)

л/г 1 » ‘

лМ

р + ]’а

где P(x) — вероятность использования последовательности x. При записи равенства в выражении (9) учтено предположение о равновероятном использовании последовательностей x, т. е. что P(x) = 1/М», где M — объем кода.

Поскольку с2(ю; x, x) = 1 для любого значения аргумента ю, то

ЦПс(ю; х(1), х'(1)) =

X x’^x 1=1

= ХХПс, (ю; х(1), х'(1))-1ППс, (ю; х(1), х(1)) =

X X’ 1=1 X 1=1

= ХХПс, (ю; х(1), х’О) — М.

X X’ 1=1

Поэтому можно записать, что

р КЕвД(а-/р)-М

пМ о р + ]а

da, (10)

где

Я(ю) = ЦП с, (ю; х(1), х'(1)). (11)

X X’ 1=1

Задача вычисления границы (10) состоит из трех этапов: получение выражения для функции D(ю), получение выражений для х.ф. с2(ю; x, x’)

и вычисление интеграла (10). Первые две задачи могут быть решены аналитически, а для решения последней задачи обычно требуется численное интегрирование.

Вывод выражения для функции D(rn)

Функция D(ro), определенная равенством (11), зависит от структуры кода (включающей канальный алфавит) и от вида х.ф. и их значений, определяемых моделью рассматриваемого канала без памяти. В частном случае — для геометрически равномерных кодов (geometrically uniform codes) — функция D(ro) может быть вычислена с использованием спектра кода. Основным примером геометрически равномерных кодов являются линейные коды в совокупности с равномерной фазовой модуляцией. В общем же случае для произвольных кодов (как блоковых, так и сверточных) и произвольных канальных алфавитов функция D(ro) может быть вычислена с использованием подходящей решетчатой диаграммы. Рассмотрим сначала случай блокового кодирования. Для описания структуры кода воспользуемся понятием решетчатой диаграммы, или кодовой решетки блокового кода. При этом описании используются терминология и определения из работы [11].

Решетчатая диаграмма представляет собой размеченный направленный граф Q = (V, E, A), где V, E, A — множество вершин, множество ребер и множество меток ребер (алфавит) соответственно. Множество ребер E состоит из троек e = (v, v’, a), v, v’ e V, a e A. Множество вершин V решетчатой диаграммы (кодовой решетки) разделяется на непересекающиеся подмножества как

V = V(0) U V(1) U…U V(n~1] U V(n),

(12)

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

где каждое множество У^ образует вершины ¿-го уровня диаграммы, I = 0, 1, …, п — 1. При этом каждое ребро е е Е начинается в вершине из У1) и заканчивается в вершине из У^+У, и каждая вершина V е V лежит хотя бы на одном из путей от вершины из множества начальных вершин У° до вершины из множества конечных вершин Уп). Представление (12) множества вершин V приводит к тому, что множество ребер может быть задано как Е = Е(1) и Е(2) и… и Е(п-1) и Е(п), где Е() — непересекающиеся подмножества, содержащие ребра, которые завершаются в вершинах из У^. Аналогично можно записать, что А = А(1) и А(2) и… и А(п-1) и А(п), где подмножества А() образуют множества меток ребер из Е(). Множества А© не обязательно должны быть дизъюнктными, т. е. не имеющими общих элементов, и во многих случаях А(1) = А(2) = … = = А(п) = А. Последовательность меток вдоль пути

в диаграмме, начинающегося в вершине из V(0) и приходящего в вершину из V-n), представляет собой кодовое слово блокового кода. Очевидно, что номер последнего уровня n равен длине блокового кода. В решетчатых диаграммах многих блоковых кодов | V(0) | = | V(n) | = 1. Примерами блоковых кодов, в решетках которых | «И0) | > 1, | Vn) > 1, могут служить циклически усеченные сверточ-ные коды (tail-biting convolutional codes). Обозначим E(i) = {0, 1, …, | У© | — 1}. Будем считать, что зафиксировано некоторое взаимно-однозначное соответствие V(i) ^ E(i), обозначаемое как E(v) = k, v e V(i), 0 < k < | V(i) | — 1. Тогда элементы множества Z(l) могут рассматриваться как индексы вершин i-го уровня. Множество Е = Е(1) U Е(2) U … U E(n-1) U Е(п) образует множество состояний решетчатой диаграммы и SQ = max^ | E(i) | = max; | V(i) | представляет собой максимальное число состояний диаграммы, которое некоторым образом характеризует ее сложность.

Отметим, что в литературе представлены формализованные процедуры построения кодовых решеток для различных блоковых кодов [11]. В частности, для любого линейного двоичного блокового кода кодовая решетка с максимальным числом состояний диаграммы SQ < min(M, 2n/M) легко строится по проверочной матрице кода. Также легко могут быть построены кодовые решетки для каскадных кодов над недвоичным алфавитом, состоящие из двоичных компонентных кодов (некоторые примеры приведены в работах [10, 12]).

Вычисление функции D(ro) базируется на использовании произведения кодовых решеток. Произведение решеток Q1 = (V1, E1, A1) и Q2 = (V2, E2, A2), где V1 = V1(0) U V(1) U…U^(л_1) U V1(n) и

V2 = v(0) U v(1) U…U V(n_1) U V(n), обозначается как Q1 x Q2 и представляет собой решетку вида Ц x ^2 = {V12, E12, A12}, где

у12 = (^(0) х ) и (^ х ^) и… и (^ х ).

Ребро е = ((„, „2), („1 , „2), (а • а2 )) е Е2 для вершин (1^, и2) е х V^ и („, „2) е ^(г+1) х У^1+1) существует в решетке х 02, если существуют ребра е1 = (v1, V!, а1) и е2 = v2, а2) в решетках и соответственно для пар вершин „ е Т^,

„1 е т1(г+1) и и2 е Т2г), и’2 е т2ш). Символ «•» обозначает здесь некоторую композицию символов а1 и а2, а алфавит произведения решеток определяется как А12 = {а1 • а2 | а1 е А1, а2 е А2}. На рис. 1 приведена поясняющая иллюстрация.

Для получения выражения для функции Б(а), определенной равенством (11), применяется ранее использовавшийся подход [10, 12]. Чтобы построить функцию .О(ю), необходимо рассмотреть все пары кодовых слов x, x’ или все

И0)

a) vT/Ob

An) „ тAn)^

а)

О! •-

е — (ui, , aj) е Е^’

б)

х («1, V2) ф-

«1 • а2

, v’2)

((vu v2Ъ (v2, v2 ), a1 ■ а2) е

По

»2

е = (v2, v2 , а1) е

(г)

■ Рис. 1. Вид ребер в исходных решетках (а) и в произведении Q1 х Q2 (б)

■ Fig. 1. The form of edges in the original trellises (а) and in the product Q1 х Q2 (б)

возможные пары путей в решетчатой диаграмме кода О = (V, E, X), E = Е(1) и Е(2) и — и Е(п), X — кодовый алфавит. Суммирование по x и x’ в (11) соответствует суммированию по всем путям в решетке О2 = О х О = {V х V, E2, {с2(ю; x, x’)}}, в которой любое ребро имеет вид ((и1, v2), (v1, v2), оДю; x, x’)), если в решетке О соответствующие ребра на одном уровне решетки имеют вид v2, х) е E(i) и (v’1, v2, x’) е E(i), x, x’ е X. Иными словами, здесь композиция меток ребер задается как x • Х = cz(ю; x, x’).

Рассмотрим сначала простой случай, когда кодовая решетка О имеет одну начальную и одну конечную вершину. В этом случае и решетка О2 имеет одну начальную и одну конечную вершину. Пусть Е— множество ребер решетки О2 на ¿-м уровне, I = 1, 2, …, п. Для уровня I определим величины

ры (ю) = X сг (ю; *’)’

где £ = Е^), I = — индексы вершин V и V’, или состояния решетки О2, т. е. р^ (ю) вычисляется как сумма меток параллельных ребер, связывающих состояния £ и I в решетке О2. Определим матрицы

Р(г)(ю) = [Р^ю)], (13)

£ = 0, 1, …, | У-1) | 2 — 1, I = 0, 1, 2, …, | У© | 2 — 1. Тогда нетрудно заметить, что

Б(ю) = Р(1) (ю)Р(2) (ю).. .Р(л) (ю). (14)

Следующий пример иллюстрирует процесс получения выражения для функции Щю) для простого нелинейного недвоичного блокового кода.

Пример. Пусть решетка О = (V Е, А), задающая некоторый блоковый код, имеет вид, показанный на рис. 2. Этот код, очевидно, имеет длину п = 4, построен над алфавитом А = {х0, х1, х2, х3} и содержит четыре кодовых слова:

(Хо Хо ^с 1 Хо), (Хо Хо Х3 Хо), (Хо Хо ^^2), (х2 Х3 Хо ^^2)’

т. е. для него М = 4. На рис. 3 показана

решетка О2 = О х О.

■ Рис. 2. Пример решетки Q = (V, E, A)

■ Fig. 2. Example of trellis Q = (V, E, A)

XyX]

■ Рис. 3. Решетка Q2 = Q х Q

■ Fig. 3. Trellis Q2 = Q х Q

Далее под композицией х • х’, представляющей собой метку ребра в решетке О2, будем понимать х.ф. с2(ю; х, х’). Поэтому для матриц P(1)(ю), P(2)(ю), P(3)(ю) и P(4)(ю) с учетом того, что с2(ю; х, х) = 1, можно записать следующие выражения:

>(1)

Р( ^ю) = [ 1 сг (ю; х0, Х2) сг (ю; , х0) 1];

Р(2)(ю) =

1 сг (ю; х0, Х1) сг (ю; XI, х0) 1

0 с2 (ю; хо, хз ) 0 с2 (ю; Х1, Х3)

0 0 с2 (ю; хз, х0) с2 (ю; хз, х^

0 0 0 1

Р(3)(ю) =

2 + с2 (ю; х1, хз ) + с2 (ю; хз, х1) 0 0 0

0 сг (ю; х1, х0) + сг (ю; хз, х0) 0 0

0 0 с2 (ю; х0, х1) + с2 (ю; х0, хз) 0

0 0 0 1

Р(4)(ю) = [1 сх (ю; х0, х2 ) сх (ю; х2, х0) 1]Т .

Вычисляя выражение для Д(ю), получаем, что

Б(ю) = Р(1) (ю)Р(2) (ю)Р(з) (ю)Р(4) (ю) = = с2(ю; х1, хз) + с2(ю; хз, х1) + с2(ю; х0, х2)сг(ю; хь хз) + с2(ю; х2, х0)сг(ю; хз, х1) + +сг (ю; х0, х!)сг (ю; х0, х2 )сг (ю; х1, х0) + с2 (ю; х0, х1)сг (ю; хь х0 )сг (ю; х2, х0) + +сг (ю; х0, х1 )сг (ю; х0, х2 )сг (ю; хз, х0) + с2 (ю; х0, хз )сг (ю; х1, х0 )сг (ю; х2, х0) +

2 2 +сг (ю; х0, х2 ) сг (ю; х0, хз )сг (ю; x1, х0 ) + сг (ю; х0, х2 ) сг (ю; х0, хз )сг (ю; x3, х0 ) +

+сг(ю; х0, х1 )сг(ю; х2, х0)2с2(ю; хз, х0) + с2(ю; х0, хз )сг(ю; х2, х0)2с2 (ю; хз, х0) + 4.

Это выражение содержит М2 = 16 слагаемых вида ^ 4=1с(ю; х(1), х'(1)) по числу пар кодовых слов x’), из них М(М — 1) = 12 нетривиальных слагаемых по числу пар x’), x ^ x’ и М = 4 тривиальных слагаемых, равных единице, по числу пар x’), x =

Если решетка О имеет несколько начальных и столько же конечных состояний, т. е. | | = | Vй | = 5, то вычисление функции Д(ю) становится чуть сложнее. Обозначим через о,, подрешетку в решетчатой диаграмме О = (V, Е, X), в которой есть только одно начальное состояние в = Е(ив), е У(0), и только одно конечное состояние в = Ци8), vs е У^, в = 0, 1, …, 5 — 1, т. е. Ов = (V,, Ев, Хв), где Vs = и V(1) и… и ^и-1) и К}. Очевидно, решетчатая диаграмма О может быть представлена как набор из в таких подрешеток О, (малых решеток) с идентичными начальными и конечными состояниями. Обозначим Ов х Ов = {V, х V,,, Е2 вв’, {с2(ю; х, х’)}} решетку, в которой каждое ребро имеет вид v2), (V,, v2), с2(ю; х, х’)), если в решетках Ов и о,,’ соответствующие ребра на одном уровне решетки имеют вид (и^, ^, х) е Е^ и

(и1, и2, х’)еЕ^!:), х,х’ е X, в,в’ = 0, 1, …, в — 1. С учетом такого представления функция Б(ю) может быть построена как

5-15-1

Я(ю) =Х X В88′ (ю),

(15)

э=0 з’=0

где

лзз, (ю) = (ю)Р^2) (ю).. РП (ю), (16)

а матрицы Р^ (ю) строятся для решеток Ов х о, по той же процедуре, по какой были построены матрицы ^(ю), I = 1, 2, …, и, для решетки О х О для случая с одной начальной и одной конечной вершинами. Очевидно, что выражение (14) — это частный случай формул (15) и (16) для случая в = | | = | У(и) | = 1.

Можно показать, что при р = 1/2, т. е. когда ю = а — у/2, выполняется равенство Д,8,(ю) = = Д,,8(ю). Поэтому равенство (15) может быть представлено как

5-1 5-1 5-1

Б(а-/ /2) =Х (а-//2) +2^ X Взз'(а-//2).

8=0 8=0 з’=8+1

Это свойство используется для уменьшения сложности вычисления верхней границы вероятности ре. Окончательное выражение для вероятности ошибки декодирования, в котором используются функции (16), имеет вид

5-1

X Озз (а-//2) +

8=0 5-1 5-1

+ 2X X пзз'(а-//2)-М

з=0 з’=з+1 -¿а. (17)

Ре ^

[ Ив пМ{

1 / 2 + /а

Отметим, что для вычисления правой части (17) нужно вычислить 5(5 + 1)/2 функций а не Б2, как это следует из формулы (15).

Упрощение для линейных кодов и аддитивных каналов

Для линейных кодов и для каналов, для которых выполняется следующее свойство для х.ф.:

, (ю; х, х’) = е2 (ю; 0, х’- х),

(18)

вычисление границы (9) может быть упрощено. Заметим, что определение разности х’ — х в этом выражении зависит от модели канала и может вычисляться по-разному для различных случаев. Примерами каналов, для которых выполняется это равенство, могут служить дискретные и непрерывные каналы с аддитивным шумом, в частности, двоичный симметричный канал и двоичный канал с аддитивным белым гауссовым шумом. Для двоичного симметричного канала разность х’ — х понимается как разность в в^(2), т. е. х’ © х. Для канала с аддитивным белым гауссовым шумом и модуляционного отображения в: в^(2) ^ (А0, А1}, А0, А1 е Ж, эта разность также понимается как х’ © х, а при вычислении значений х.ф. используются условные гауссовы ф.п.в. со средними в(0) и в(х’ © х). В этом случае двойная сумма по словам кода в выражении (9) может быть представлена как

XXП

х х’х 1=1

е,(а;х(1),х'(1)) =

)=XXП>; 0, х’-х(1)) =

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

х х’х 1=1

-X X П^ (ю; 0, х(1) — х'(1)) =

х х’-х* 0 1=1

= М Xffc (ю; 0, х(1)) =

х*0 1=1

( п Л

(19)

= М

XП(ю; 0, х(1)) -1

V х 1=1

(20)

где в переходе от (19) к (20) использовано свойство линейности кода. Для представления суммы по x в (20) рассмотрим решетку вида О, х О, где О» = {{и0}и{^0} и… и{^0}, Е, {0}} — решетка, содержащая лишь одну вершину на каждом уровне и только один путь из начальной вершины в конечную, отмеченный нулевыми символами. Тогда сумму по кодовым словам x в (20) можно представить как

А (ю) = XП(ю; 0, х(1)) =

х 1=1

= Р11)(ю)Р1(2)(ю)…Р1п)(ю),

(21)

где матрицы Р-|1)(ю) строятся на основе решетки О» х О аналогично тому, как были построены матрицы (13) на основе решетки О х О. То есть Р1° (ю) = [Р^ 1 (ю)], где

р1% (ю) =

е(и,и’,сг (ю;0,х))еЕ(1)

ег (ю; 0, х),

к = Е(и), I = Е(и’) — индексы вершин V и V’, или состояния решетки О» х О, а Е() — множество ребер ¿-го уровня в решетке О» х О. Иными словами, Р^Ы(ю) вычисляется как сумма меток параллельных ребер, связывающих состояния к и I в решетке О» х О. Граница для ре в окончательном виде выглядит следующим образом:

Ре

] Ив

Р (а — /р) -1

Р + /а

¿а.

(22)

Граница (22), в которой используется функция Д1(ю), вычисляемая по формуле (21), совпадает с обычной аддитивной границей ошибки декодирования для линейного кода и канала с аддитивным шумом (дискретным или непрерывным). При этом сложность ее вычисления определяется сложностью решетки О, а не решетки О х О, как в общем случае.

Предложенный подход с использованием стандартной техники [2] может быть легко распространен на случай решетчатых и сверточных кодов. Тогда нетрудно показать, что, например, для двоичного сверточного кода со скоростью

И = к/и с функцией нумератора весов Т(Б, Ы) [2] границы для вероятности ошибочного события РЕ и вероятности ошибки на бит Рв принимают вид

PE < — f Re

тг J

T(cz (a-/P; 0, 1), 1)

P + ]’a

к f

PB << f Re -k i

1 dT(Cz (a-]P; 0, 1), N)

P + ]a

da;

N=1

da. (23)

Заметим, что обычная граница вероятностей РЕ и Рв для сверточных кодов имеет вид Ре< Т(Б0, 1),_ Рв < (1/^^, М)/йМ| N = 1, где

£>0 = т1пр>0 еРг(у|х,х) — показатель границы Чернова. В некоторых случаях эти границы могут быть улучшены за счет введения коэффициента К(й)~ 1/>/й; конкретный вид функции К(й) зависит от модели канала [2, 4]. Границы в этом случае принимают вид РЕ < К(й/)Т(Б0, 1), Рв < К/УЩТ^, N)/dN | Ы = ^ где ^ — свободное расстояние сверточного кода.

Примеры применения

В этом разделе приведены примеры применения границы (10) для некоторых каналов. Для простых случаев — двоичный симметричный канал и гауссов канал с дискретным временем — предложенный подход приводит, как и ожидалось, к известным результатам. Для более сложных моделей канала, рассмотренных в примерах 3-5, использование границы (10) позволяет получить новые результаты.

Пример 1. Двоичный симметричный канал (ДСК). В этом случае х, у = 0, 1 и рх | у(х | у) = 1 — е, если у = х, и рх| у(х I у) = е, если у Ф х, где е — вероятность ошибки в ДСК, е < 1/2. Характеристическая функция (8) имеет в этом случае вид

с(ю; х, х) =^(1-е)1-;»е’»+е1-‘»(1-е)’», хФх-. ^

I 1, ^С — ^с .

Граница для вероятности ре вычисляется в общем виде согласно выражению (10). Если выделить и рассмотреть одно слагаемое в сумме по x в (11), то получим выражение для вероятности Ре^ ^ x’ | x) [см. (3)] следующего вида:

Pe (x ^ x’ | x) =1 f Re i=1

ТГ

ПCz (a-]’P; x(l), x'(l))

P + ]a

-da =

1 f Re

IT J

f (s, a -]’P)

— ]P)dH(x,x’)

P + ]’a

-da,

(25)

где /(е, ю) = (1 — е)1->е/® + е1->(1 — еУш; й^, x’) — расстояние Хэмминга между словами x и x’. Обозначим й = йд^, x’) и и = 1п((1 — е)/е); тогда можно записать, что /(е, ю) = (1 — е)е-^ши + ееюи и далее легко показать, что

— т)ан (х,х’) =

f (s, a -]’P)

liu(d-2l)a Bu(d-2l)

Zd nl d-ln sl l=0 Cds (1 -s) e

Отсюда и из (25) следует, что Pe (x ^ x’ | x) = X d=0 Cd sd-l (1 — s)1 ePu(d-2l) I(d — 2 Z),

где обозначение I(m) используется для следующего интеграла:

1 к ]ma 1 к п — к .

,-/ ч 1 Гтт e _ 1 гPcosma _ 1 asinma _ I (m) = — I Re-— da = — I —2-^da + — I ——— da.

ТГ J ft — 1Г/ ТГ J Q2 1 ТГ J

ж0 Р-;а ж0 Р2 ж0 Р2 +«2

Для вычисления этих величин используем табличные тождества

г cos ma

J r2 . 2 0 P +a

da =

г a sin ma

J P2 +a2

da = <

^e»mP, m > 0,

—emP, m < 0;

-e»mP, m > 0, 2

0, m = 0,

—

—emP, m < 0,

где P > 0, и тогда получим, что

I (d — 2l) =

rP(d-2l), d > 2l,

-, d = 2l, 2

0, d < 2l,

и поэтому

Pe (x ^ x’ | x) =

X Cdsl (1 — s)d l, d — нечетное,

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

l=(d+1)/2

1 cd/2sd/2 (1 -s)d/2 + d-

+ X cdsl (1 -s)d-l, d — четное.

l=d/2+1

Последнее равенство означает, что граница (10) для этого случая совпадает с аддитивной границей, в которой каждое слагаемое вычисляется точно.

Для х.ф. (24) выполняется условие (18). Поэтому граница для вероятности pe для линейного кода, которая может быть найдена согласно выражению (22), дает в точности тот же результат, что и граница (10), но вычисляется значительно проще.

Пример 2. Гауссов канал с дискретным временем. Для этого примера выход канала имеет вид у() = 8(х(^) + где 8(х(^) — переданная сигнальная точка, в(х(1)), у(1), е Ж ш, где ш — размерность сигнального пространства, — ш-мерный гауссов случайный вектор с независимыми одинаково распределенными компонентами с параметрами (0, ст2). Условная ф.п.в., определяющая канал, задается поэтому следующим образом:

Py-

. (y s(x)) = (л&Гт exp(-||y — s(x)|I2 / 2a2).

Нетрудно показать, что х.ф. (8) имеет в этом случае вид

cz (ю; x, x’) = exp

С II 1|2

/ю(1 — /ю) s(x) -s(x’)1

2a2

. (26)

Тогда для двух кодовых слов x = (х(1), …, х(п)), x’ = (х'(1), …, х'(га)) и их модуляционных отображений s(x) = (в(х(1)), …, 8(х(га))) и s(x’) = (в(х'(1)), …, в(хг(п))) можно записать, что

Пcz (ю; x(l), x'(l)) = exp l=1

/ 2 л

/ю(1 — /ю)й

ю=а-/р

a2d2 /a(1-2p)d2 P(1-P)d2

= e 2a2

2a2

где

d2 = d2E(s(x), s(x’)) = Xl=1

s(x(l)) — s(x'(l))

(l)

Если выделить и рассмотреть одно слагаемое в сумме по x в (11), то получим выражение для вероятности Р^ ^ x’ | x) [см. (3)] вида

Ре (х ^ х’ | х) =

р(1-р)^2 х 2 2 2 = 1 хИввхр(- (а2 + /а(1 -Р))^2 / 2ст2) ¿а

I, в Р + /а а.

Для сокращения записи введем обозначения а = ¿2 / 2ст2, и = (1 — 2р)й2 / 2ст2. (27)

Тогда для вероятности Ре^ ^ x’ | x) можно записать выражение

Ре (х ^ х’ | х) = е»ар(1-р)1(а, и), (28)

где

1 то e~aa + /au

I(a, u) = — f Re-da =

л 0 P + /а

то -aa2/ • •

1 г e (cos ua-/ sin ua)

=1 f Re

TT J

P + /a

da =

1 то -aa 1 то -aa

1_ re cos ua . 1 r ae sin ua

=^I

-da—f-

TT J

л 0 P2 +a2 л 0 р2 +a2

1 aP2+

d a =

=1 еар +ри ег^(^р + и / (2Та)). (29)

Последнее выражение в (29) получено с использованием табличных интегралов для условий а > 0, р > 0, у > 0:

х —ах

■е ТО8ху ¿х = еар2 (е-ру

0 P2 + x2 4P

fe_Py erfc(i1) +ePy erfc(t2));

f sinxydx =лeaP2 fe-Pyerfc(i1)-ePyerfc(i2)V

0 P2 + x2 4 V >

где ^ = -[йр — у /(2л/а); í2 = л/ар + у /(2л/а). Собирая вместе выражения (28), (29) и (27), получаем в итоге, что

Ре (х ^ х’ | х) = 1 ет*с Г V

2 V )

= Q

dE (s(x), s(x’))

Это значит, что граница (10) для этого случая совпадает с аддитивной границей, в которой каждое слагаемое вычисляется точно.

Если для модуляционного отображения s(x) выполняется свойство ||s(x) — s(x’)||2 = ||s(0) — s(x’ — x)||2, а код обладает свойством линейности, т. е. x — x’ принадлежит коду, то граница для вероятности pe, которая может быть найдена согласно выражению (22), дает в точности тот же результат, что и граница (10), но вычисляется гораздо проще.

Далее рассматриваются примеры, которые не сводятся к ранее известным аддитивным границам.

Пример 3. Канал с гауссовым шумом, дисперсия которого зависит от переданного значения (Input dependent additive Gaussian noise — ID-AGN). Эта модель используется при анализе систем записи/считывания данных в многоуров-

невой флеш-памяти, беспроводных систем связи в видимом оптическом диапазоне, волоконно-оптических систем связи, систем связи с неортогональным множественным доступом [13-21].

Первым среди далее приводимых вариантов мы рассматриваем тот, который использовался для описания модели ячейки многоуровневой флеш-памяти (гауссова аппроксимация [13, 14]).

Входные уровни каждой ячейки принимают некоторые фиксированные значения х

хд-1, а выходные значения представляют собой случайные величины. Распределения этих случайных величин описываются условными ф.п.в. Ру|х(у | х), -<» < у < <», х = х0, хх, …, х^.

В публикациях [13-15] перечисляются факторы, определяющие конкретный вид условных ф.п.в. Ру|х(у| х), -да < у < да, х = х0, хр …, хд-1. Будем полагать далее, что модель ячейки определяется ф.п.в. ру|х(у | х), I = 0, 1, …, q — 1, которые могут быть аппроксимированы гауссовыми плотностями, т. е. будем считать, что

Рух(У 1 х) =

-/2лст(х; )

ехр

( (У — х)2 ^ 2ст2 (х;)

Эта модель известна также как ID-AGN-модель [22]. Пример с q = 4 часто используется для описания канала записи флеш-памяти, который в этом случае представлен как набор одиночных многоуровневых ячеек памяти. Эта модель допускает обобщение на большее число входных уровней, в частности на шесть, восемь и двенадцать уровней [22]. С возрастанием числа циклов перезаписи и увеличением времени хранения записанных данных значения уровней записи х1 (кроме х0) уменьшаются, тогда как значения стандартного отклонения ст(х^) (кроме ст(х0)) увеличиваются. Такое изменение параметров х1 и ст(х), задающих канал, описывает процесс его постепенного ухудшения (деградации) в зависимости от времени и условий эксплуатации. Детали описания зависимости величин х1 и ст(х^), I = 0, 1, …, q — 1, от числа циклов перезаписи и времени хранения записанных данных могут быть найдены в работах [13, 14, 23].

В этом случае можно показать, что при ст(х) Ф ст(х’)

с2 (ю; х, х’) =

ехр

ст(х) Уюст(х’)1->ю ^/юст2 (х) + (1 — /ю)ст2 (х’)

/ю(1 — /ю)(х — х’) 2(/юст2 (х) + (1 — /ю)ст2 (х’))

(30)

при условиях 1тю < ст2(х’)/(ст2(х) — ст2(х’)), если ст(х) > ст(х’), и -1тю < ст2(х’)/(ст2(х) — ст2(х’)), если ст(х) < ст(х’). Граница для вероятности ре вычис-

ляется для этой модели с использованием общего выражения (10). Ряд результатов, относящихся к каналу записи флеш-памяти и полученных на основе описанного здесь подхода, может быть найден в работах [10, 12].

Модель с ID-AGN, используемая для описания взаимосвязи входного сигнала х и выходного сигнала у в беспроводной системе связи в видимом оптическом диапазоне и волоконно-оптической системе связи, имеет следующий вид [16, 17]:

У = ах+л/а0+~%Х + £,

(31)

где g — коэффициент передачи канала; к0, > 0 — коэффициенты, учитывающие вклад ID-AGN; £1 и £ — независимые гауссовы случайные величины с нулевым средним и дисперсиями ст^ и ст соответственно. Первая составляющая

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

I + % х аддитивного шума возникает вследствие случайности механизма эмиссии фотонов светодиодом. Вторая составляющая £ аддитивного шума представляет собой обычный тепловой шум. Передаваемый сигнал х в (31) представляет собой случайную величину, которая в АМ, простейшем варианте модуляции, характеризует интенсивность излучаемого оптического сигнала. Очевидно, при использовании АМ х является неотрицательной случайной величиной, ограниченной сверху максимальной интенсивностью светодиода. Значения х.ф. с2(ю; х, х’) для этой модели вычисляются по формуле (30), в которой зависимость ст(х) имеет вид

I 2 2

ст(х) = (*0 + Щ^х)стI +ст .

Пример 4. Канал с релеевскими замираниями и непрерывным выходом. В этой модели входные величины х е {х0, х1}, а выход канала (выходное значение демодулятора с мягкими решениями) может быть представлен как у = у0 — у1, где

У0 =

|(Сс727 + ^0 )2 + (Сал/ЗТ + £а0) , если х = х0, Й0 +£вю, если х = х1;

У1 =

+ £вй, если х = х0,

(С^л/2у)2 + (С^л/2Т + £а1 )2

если х = х1,

и Сс, Св, £с0, £в0, £с1, £в1 — независимые гауссовы случайные величины с нулевыми средними. Величины £с0, £в0, £с1, £в1 возникают из-за влияния аддитивного белого гауссова шума, а Сс и Св представляют собой квадратурные компоненты релеевского коэффициента передачи канала.

2 2

При соответствующей нормировке Сс = Св = 1 / 2,

2 2 2 2 £с0 =£в0 =£с1 =£й1 = 1, а величина у имеет смысл

среднего значения отношения сигнал/шум. Такая модель возникает при рассмотрении некоге-

рентного приема ортогональных сигналов ЧМ-2, переданных по каналу с релеевскими замираниями. Для условных ф.п.в. в этом случае справедливы выражения

Рух(Ух0) =

2(7 + 2)

exp

2(у + 1)

если y >0,

1 I У

■expI — I, если y < 0;

2(7 + 2) Ч2}’ У ‘

(32)

Pyx(y xl) = Рух(-У x0 ) = -1-exp|-У |, если у > 0,

2(7 + 2) ^ 2J У ‘

exp

2(7 + 2) Ч 2(7 + 1)

если у < 0.

Подстановка выражений (32) и (33) в (8) приводит в итоге к выражению

10°

-2

-3

-5

-6

-8

ДСК, АБГШ, ФМ-2, жесткое квантование, код (13,15)

………………………………. ………………………………………………ii

ЛуЧ, ! 1 s |

L t г 3 :

4 i s

Ё NjN •

: : : : г 4 ::::: i :::: IV ::: i : :

j j j j X i i

10 11 12 13

8 9

V дБ

— без кода, Рв =

— Рв, гр. Чернова + аддитивная граница

— Рв, гр. Чернова (уточненная) + аддитивная граница

— Рв, х.ф. + численное интегрирование

100

-4

-6

-8

АБГШ, ФМ-2, непрерывный выход, код (13,15)

iiiiiiiiiiiiiiiiiiiiiiiiii

Mi ;;;;;;;;;;;

-•V—Y

……………………..l-NqriTrrr . . .

nitirmm ………………i…………—V IT] Till Т1Т1ТГ1Т1Т1Т! Till! ГШ1Т1Т!Т1Т1ТГ1Т]Т1Т!Т1ТГ!|1^Т1Т!Т1ТГТ1Т1

………..

::: ……………………

……………. …………………..

8 10

V дБ

без кода, Рв = ф(^2уь)

Рв, гр. Чернова + аддитивная граница

Рв, гр. Чернова (уточненная) + аддитивная граница

Рв, х.ф. + численное интегрирование

Релей, ЧМ-2, непрерывный выход, код (13,15)

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

13 14 15 16 17 18 19 20 21 22 23

1Ь, дБ

— без кода, Рв = 1/(2 + Уь)

— Рв, гр. Чернова + аддитивная граница

— Рв, гр. Чернова (уточненная) + аддитивная граница

— Рв, х.ф. + численное интегрирование

101

Лаплас, непрерывный выход, код (13,15)

-2

-5

-6

12 13 14

17 18 19

15 16

ь дБ

— без кода, Рв = ехр(-л/2уЬ/2)2

— Рв, гр. Чернова + аддитивная граница

_ Рв, х.ф. + численное интегрирование

■ Рис. 4. Границы вероятности ошибки на бит PB в зависимости от отношения сигнал/шум на бит 7b для рассмотренных моделей каналов

■ Fig. 4. Bounds on the bit error probability PB vs signal-to-noise ratio per bit 7b for the considered channel models

са (ю; Xо, х1) =

у + 1

у + 21 1 + (1 -/ю)у 1 + /юу

, (34)

при этом должны выполняться условия 1/у > 1тю > -(1 + у)/у. В дальнейшем потребуется значение правой части (34) при ю = а — /р. Из условий для 1тю следует, что -1/у < р < (1 + у)/у. Кроме того, имеется ограничение р > 0. Поэтому окончательно имеем границы для параметра р: 0 < р < (1 + у)/у. Тогда для р = 1/2 получаем

г(а-1 / 2; х0, х1) =

4(у + 1)

(у + 2)2 +4а2 у2

(35)

Пример 5. Канал с аддитивным шумом с распределением Лапласа. Эта модель является частным случаем модели канала с аддитивным шумом, имеющим обобщенное гауссово распределение. Аддитивный шум, имеющий распределение Лапласа, широко используется как а) модель интерференционного шума в системах связи миллиметрового диапазона; б) модель интерференционного шума в дуплексных радиосетях при наличии замираний; в) модель шума в оптических линиях [19-21]. В этой модели предполагается, что х е {х0, х1}, х0, х1 е Ж, и условные ф.п.в. задаются равенствами рух(у | х0) = ехр(- | у — х0 | /Ь)/(2Ь) и

Рух(у I хх) = ехр(- | у — хг | /Ь)/(2Ь), где Ь = стД/2, ст — среднеквадратическое отклонение. Подстановка этих выражений для ф.п.в. приводит после ряда преобразований к следующему выражению для х.ф.:

с2 (ю; х0, х1) =

= ((1 -/ю)е~^°1х0-х1/Ь — /юе»(1- 1ю)1 х0-х1 >/Ь ) / (1 — 2/ю).

Более удобным для практических вычислений оказывается функция с2(ю; х, х’)|ю = а-/2, которая может быть приведена к виду

сг (а-;/2; х0, =

-х—1 ^дт(а|х0 -х± /Ь)

2Ь

2а

+ ео8(а(х0 -х^) / Ь)

. (36)

В приведенных ниже численных примерах под значением отношения сигнал/шум понимается величина | х0 — х1 | /Ь.

Численные результаты. В качестве иллюстративного примера рассмотрим применение разработанного подхода для двоичного сверточ-ного кода с Я = 1/2 с многочленной порождающей матрицей С(г) = [1 + г + 23 1 + г2 + г3], или в восьмеричной компактной записи С(г) = [13, 15]. Этот код имеет кодовое ограничение V = 3,

свободное расстояние ^ = 6 и функцию нумератора весов

Т(£, Ы) =

£6 Ыз — £10Ыз + £6 N 1 — 2£2Nз — з£2N + 2£6Nз

На рис. 4 представлены графики границы вероятности Рв, вычисленные согласно выражению (23) для рассмотренных примеров каналов, исключая модель с ГО-ЛОМ [см. (24), (26), (34) и (36)]. Результаты, относящиеся к модели с ГОЛОМ полученные с использованием описанного здесь подхода, могут быть найдены в работах [10, 12].

Из приведенных графиков следует, что предложенный универсальный подход (красная линия) дает существенное улучшение границы вероятности ошибки для конкретных кодов по сравнению с обычной аддитивной границей в комбинации с границей Чернова (синяя линия): так, при вероятности ошибки 10-5 оценка требуемых энергетических затрат снижается на величину от 0,7 до 2,0 дБ в зависимости от модели канала. Что касается уточненных вариантов границы Чернова [4] (черная линия), то предложенный подход тоже улучшает известные границы для этих моделей, хотя и очень незначительно. Заметим, что важнейшая положительная черта предложенного подхода состоит в его универсальности, что позволяет применить его к любому каналу без памяти и обеспечить при этом высокую точность оценивания при малых вычислительных затратах.

Заключение

В данной работе представлен метод точного вычисления аддитивной границы вероятности ошибочного декодирования для широкого класса кодов и моделей каналов без памяти. Разработанный метод базируется на получении точного выражения для попарной вероятности ошибки с использованием аппарата характеристических функций. Получение аддитивной границы вероятности ошибочного декодирования основано на использовании произведения решетчатых диаграмм для рассматриваемого кода, позволяющего получить итоговое выражение в интегральной форме, удобной для численного интегрирования. Важной особенностью предложенной процедуры является то, что она позволяет точно вычислить аддитивную границу с помощью подхода, основанного на использовании передаточных (производящих) функций. При таком подходе метки ветвей в произведении решетчатых диаграмм для рассматриваемого кода заменяются соответствующими характеристи-

ческими функциями. Удобное для численного интегрирования итоговое выражение позволяет вычислять значения аддитивной границы вероятности ошибочного декодирования с желаемой точностью. В целом, как показывают конкретные примеры, вычислительные затраты при использовании предложенного подхода к вычислению аддитивной границы вероятности ошибочного декодирования оказываются вполне приемлемыми для кодов, имеющих сравнительно небольшую длину.

Результаты были частично представлены на XXIV международной конференции «Волновая электроника и инфокоммуникационные систе-

1. Proakis J. G., M. Salehi M. Digital Communications. Fifth Ed. McGraw-Hill, 2008. 1151 p.

2. Gallager R. G. Principles of Digital Communications. Cambridge University Press, 2012. 407 p.

3. I. Sason I., Shamai S. Performance analysis of linear codes under maximum-likelihood decoding: A tutorial. Foundations and Trends in Communications and Information Theory, 2006, vol. 3, no. 1-2, pp. 1-225.

4. Trofimov A. N. Modified Chernoff Bound and Some Applications. In: Modulation and Coding Techniques in Wireless Communications. Ed. E. Krouk and S. Se-menov. Wiley, 2011. Pp. 206-220.

5. Biglieri E. Coding for Wireless Channels. Springer US, 2006. 420 p.

6. Goldsmith A. Wireless Communications. Cambridge University Press, 2012. 644 p.

7. Abedi A., Khandani A. K. An analytical method for approximate performance evaluation of binary linear block codes. IEEE Transactions on Communications, 2004, vol. 52, no. 2, pp. 228-235.

8. Ali S. A., Kambo N. S., Ince E. A. Exact expression and tight bound on pairwise error probability for performance analysis of turbo codes over Nakagami-m fading channels. IEEE Communications Letters, 2007, vol. 11, no. 5, pp. 399-401.

9. Gupta B., Saini D. S. Moment generating function-based pairwise error probability analysis of concatenated low density parity check codes with alam-outi coded multiple iinput multiple output orthogonal frequency division multiplexing systems. Communications IET, 2014, vol. 8, no. 3, pp. 399-412.

10. Таубин Ф. А., Трофимов А. Н. Каскадное кодирование на основе многомерных решеток и кодов Рида — Соломона для многоуровневой флэш-памяти. Труды СПИИРАН, 2018, вып. 2(57), с. 75103. doi:10.15622/sp.57.4

11. Vardy A. Trellis Structures of Codes. In: Handbook of Coding Theory. Ed. V. S. Pless and W. C. Huffman. Elsevier, Amsterdam, 1998. Vol. 2. 1106 p.

мы (WEC0NF-2021)», Санкт-Петербург, ГУАП, 2021 г.

Финансовая поддержка

Работа выполнена при финансовой поддержке Министерства науки и высшего образования Российской Федерации, соглашение № FSRF-2020-0004 «Научные основы построения архитектур и систем связи бортовых информационно-вычислительных комплексов нового поколения для авиационных, космических систем и беспилотных транспортных средств».

12. Таубин Ф. А., Трофимов А. Н. Каскадное кодирование для многоуровневой флэш-памяти с исправлением ошибок малой кратности во внешней ступени. Труды СПИИРАН, 2019, вып. 18(5), с. 11491181. doi:10.15622/sp.2019.18.5.1149-1181

13. Wang X., Dong G., Pan L., Zhou R. Error correction codes and signal processing in flash memory. In: Flash Memories. Ed. Igor Stievano. http://www.in-techopen.com/books/flash-memories/error-correc-tion-codes-and-signal- processing-in-flash-memory (дата обращения: 26.10.2014).

14. Dong G., Pan Y., Xie N., Varanasi C., Zhang T. Estimating information-theoretical NAND flash memory storage capacity and its implication to memory system design space exploration. IEEE Trans. Very Large Scale Integration (VLSI) Systems, 2012, vol. 20, no. 9, pp. 1705-1714.

15. Huang X., Kavcic A., Ma X., Dong G., Zhang T. Multilevel flash memories: Channel modeling, capacities and optimal coding rates. International Journal on Advances in Systems and Measurement, 2013, vol. 6, no. 3, 4, pp. 364-373. http://www.iariajournals.org/ systems_and_measurements/ (дата обращения: 26.10.2014).

16. Moser S. M. Capacity results of an optical intensity channel with input-dependent Gaussian noise. IEEE Transactions on Information Theory, 2012, vol. 58, no. 1, pp. 207-223.

17. Yuan M., Sha X., Liang X., Jiang M., Wang J., Zhao C. Coding performance for signal dependent channels in visible light communication system. Signal and Information Processing (GlobalSIP) 2015 IEEE Global Conference, pp. 1037-1041.

18. Gao Q., Hu S., Gong C., Xu Z. Modulation design for multi-carrier visible light communications with signal-dependent noise. Communication Systems (ICCS) 2016 IEEE International Conference, 2016, pp. 1-6.

19. Dytso A., Bustin R., Poor H. V., Shitz S. S. On additive channels with generalized Gaussian noise. Proceedings of the IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 2017, pp. 426-430.

20. Ding Z., Yang Z., Fan P., Poor H. V. On the performance of non-orthogonal multiple access in 5G systems with randomly deployed users. IEEE Signal Process. Letters, 2014, vol. 21, no. 12, pp. 1501-1505.

21. Bariah L., Muhaidat S., Sofotasios P. C., Gurugopi-nath S., Hamouda W., Yanikomeroglu H. Non-orthogonal multiple access in the presence of additive generalized Gaussian noise. IEEE Communications Letters, 2020, vol. 24, no. 10, pp. 2137-2141.

22. Sun F., Rose K., Zhang T. On the use of strong BCH codes for improving multilevel NAND flash memory

storage capacity. http://www.researchgate.net/publi-cation/254376882_On_the_Use_of_Strong_BCH Codes for Improving_Multilevel NAND Flash_ Memory Storage Capacity (дата обращения: 26.10.2014).

23. Трофимов А. Н., Таубин Ф. А. Теоретико-информационный анализ многоуровневой flash-памяти. Часть 1: Модель канала и границы случайного кодирования. Информационно-управляющие системы, 2016, № 2, с. 56-67. doi.org/10.15217/issn1684-8853.2016.2.56

UDC 621.391

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

doi:10.31799/1684-8853-2021-4-71-85

Evaluation of the union bound for the decoding error probability using characteristic functions

A. N. Trofimova, PhD, Tech., Associate Professor, orcid.org//0000-0003-1233-5222, andrei.trofimov@k36.org F. A. Taubina, Dr. Sc., Tech., Professor, orcid.org/0000-0002-8781-9531

aSaint-Petersburg State University of Aerospace Instrumentation, 67, B. Morskaia St., 190000, Saint-Petersburg, Russian Federation

Introduction: Since the exact value of a decoding error probability cannot usually be calculated, an upper bounding technique is used. The standard approach for obtaining the upper bound on the maximum likelihood decoding error probability is based on the use of the union bound and the Chernoff bound, as well as its modifications. For many situations, this approach is not accurate enough. Purpose: Development of a method for exact calculation of the union bound for a decoding error probability, for a wide class of codes and memoryless channels. Methods: Use of characteristic functions of logarithm of the likelihood ratio for an arbitrary pair of codewords, trellis representation of codes and numerical integration. Results: The resulting exact union bound on the decoding error probability is based on a combination of the use of characteristic functions and the product of trellis diagrams for the code, which allows to obtain the final expression in an integral form convenient for numerical integration. An important feature of the proposed procedure is that it allows one to accurately calculate the union bound using an approach based on the use of transfer (generating) functions. With this approach, the edge labels in the product of trellis diagrams for the code are replaced by their corresponding characteristic functions. The final expression allows, using the standard methods of numerical integration, to calculate the values of the union bound on the decoding error probability with the required accuracy. Practical relevance: The results presented in this article make it possible to significantly improve the accuracy of the bound of the error decoding probability, and thereby increase the efficiency of technical solutions in the design of specific coding schemes for a wide class of communication channels.

Keywords — maximum likelihood decoding, union bound on the error probability, pairwise error probability, characteristic function, ID-AGN channel, additive Laplacian noise channel.

References

1. Proakis J. G., M. Salehi M. Digital Communications. Fifth Ed. McGraw-Hill, 2008. 1151 p.

2. Gallager R. G. Principles of Digital Communications. Cambridge University Press, 2012. 407 p.

4. Trofimov A. N. Modified Chernoff Bound and Some Applications. In: Modulation and Coding Techniques in Wireless Communications. Ed. E. Krouk and S. Semenov. Wiley, 2011. Pp. 206-220.

5. Biglieri E. Coding for Wireless Channels. Springer US, 2006. 420 p.

6. Goldsmith A. Wireless Communications. Cambridge University Press, 2012. 644 p.

7. Abedi A., Khandani A. K. An analytical method for approximate performance evaluation of binary linear block codes. IEEE Transactions on Communications, 2004, vol. 52, no. 2, pp. 228-235.

8. Ali S. A., Kambo N. S., Ince E. A Exact expression and tight bound on pairwise error probability for performance analysis of turbo codes over Nakagami-m fading channels. IEEE Communications Letters, 2007, vol. 11, no. 5, pp. 399-401.

9. Gupta B., Saini D. S. Moment generating function-based pairwise error probability analysis of concatenated low density parity check codes with alamouti coded multiple iinput multiple output orthogonal frequency division multiplexing systems. Communications IET, 2014, vol. 8, no. 3, pp. 399412.

10. Taubin F. A., Trofimov A. N. Concatenated Reed-Solomon/ lattice coding for multilevel flash memory. SPIIRAS Proceedings, 2018, no. 2(57), pp. 75-101 (In Russian). doi: 10.15622/sp.57.4

11. Vardy A. Trellis Structures of Codes. In: Handbook of Coding Theory. Ed. V. S. Pless and W. C. Huffman. Elsevier, Amsterdam, 1998. Vol. 2. 1106 p.

12. Taubin F. A., Trofimov A. N. Concatenated coding for multilevel flash memory with low error correction capabilities in outer stage. SPIIRAS Proceedings, 2019, vol. 18, no. 5, pp. 1149-1181 (In Russian). doi:10.15622/sp.2019.18.5.1149-1181

13. Wang X., Dong G., Pan L., Zhou R. Error correction codes and signal processing in flash memor. In: Flash Memories. Ed. Igor Stievano. Available at: http://www.intechopen. com/books/flash-memories/error-correction-codes-and-signal-processing-in-flash-memory (accessed 26 October 2014).

15. Huang X., Kavcic A., Ma X., Dong G., Zhang T. Multilevel flash memories: Channel modeling, capacities and optimal coding rates. International Journal on Advances in Systems and Measurement, 2013, vol. 6, no. 3, 4, pp. 364-373. Available at: http://www.iariajournals.org/systems_and_meas-urements/ (accessed 26 October 2014).

16. Moser S. M. Capacity results of an optical intensity channel with input-dependent Gaussian noise. IEEE Transactions on Information Theory, 2012, vol. 58, no. 1, pp. 207223.

21. Bariah L., Muhaidat S., Sofotasios P. C., Gurugopinath S., Hamouda W. Yanikomeroglu H. Non-orthogonal multiple access in the presence of additive generalized Gaussian noise. IEEE Communications Letters, 2020, vol. 24, no. 10, pp. 2137-2141.

22. Sun F., Rose K., Zhang T. On the use of strong BCH codes for improving multilevel NAND flash memory storage capacity. Available at: http://www.researchgate.net/publica-tion/254376882_On_the_Use_of_Strong_BCH Codes for Improving_Multilevel NAND Flash_Memory Storage Capacity (accessed 26 October 2014).

23. Trofimov A. N., Taubin F. A. Information theory analysis of multilevel flash memory. Part 1: Channel model and random coding bounds. Informatsionno-upravliaiushchie siste-my [Information and Control Systems], 2016, no. 2, pp. 5667 (In Russian). doi.org/10.15217/issn1684-8853.2016.2.56

ПАМЯТКА ДЛЯ АВТОРОВ

Поступающие в редакцию статьи проходят обязательное рецензирование.

При наличии положительной рецензии статья рассматривается редакционной коллегией. Принятая в печать статья направляется автору для согласования редакторских правок. После согласования автор представляет в редакцию окончательный вариант текста статьи.

Процедуры согласования текста статьи могут осуществляться как непосредственно в редакции, так и по е-таП (ius.spb@gmail.com).

При отклонении статьи редакция представляет автору мотивированное заключение и рецензию, при необходимости доработать статью — рецензию.

Редакция журнала напоминает, что ответственность за достоверность и точность рекламных материалов несут рекламодатели.

Источник

8.5. Блочные линейные коды

8.5.1. Математическое описание процессов кодирования и декодирования

Предложите, как улучшить StudyLib

Не пропустите эти материалы по теме: