Уровень
значимости — это вероятность того, что
мы сочли различия существенными, а они
на самом деле случайны.
Когда
мы указываем, что различия достоверны
на 5%-ом уровне значимости, или при р<0,05,
то мы имеем виду, что вероятность того,
что они все-таки недостоверны, составляет
0,05.
Когда
мы указываем, что различия достоверны
на 1%-ом уровне значимости, или при р<0,01,
то мы имеем в виду, что вероятность того,
что они все-таки недостоверны, составляет
0,01.
Если
перевести все это на более формализованный
язык, то уровень значимости — это
вероятность отклонения нулевой гипотезы,
в то время как она верна.
Ошибка,
состоящая в том, что мы отклонили нулевую
гипотезу, в то время как она верна,
называется ошибкой 1 рода.
Вероятность
такой ошибки обычно обозначается как
а. В сущности, мы должны были бы указывать
в скобках не р<0,05 или р<0,01, а а<0,05
или <Х<0,01. В некоторых руководствах
так и делается (Рунион Р., 1982; Захаров
В.П., 1985 и др.).
Если
вероятность ошибки — это а, то вероятность
правильного решения: 1—а. Чем меньше а,
тем больше вероятность правильного
решения.
Исторически
сложилось так, что в психологии принято
считать низшим уровнем статистической
значимости 5%-ый уровень (р<0,05): достаточным
— 1%-ый уровень (р^О.01) и высшим 0,1% -ый
уровень (р<0,001), поэтому в таблицах
критических значений обычно приводятся
значения критериев, соответствующих
уровням статистической значимости
р<0,05 и р<0,01, иногда — р<0,001. Для
некоторых критериев в таблицах указан
точный уровень значимости их разных
эмпирических значений. Например, для
ф*=1,56 р=0,06.
До
тех пор, однако, пока уровень статистической
значимости не достигнет р=0,05, мы еще не
имеем права отклонить нулевую гипотезу.
Правило
отклонения HQ и принятия Hi
Если
эмпирическое значение критерия равняется
критическому значению, соответствующему
р^0,05 или превышает его, то HQ отклоняется,
но мы еще не можем определенно принять
W.
Если
эмпирическое значение критерия равняется
критическому значению, соответствующему
р<0,01 или превышает его, то HQ отклоняется
и принимается Н^.
Исключения:
критерий
знаков G, критерий Т Вилкоксона и критерий
U Манна-Уитни. Для них устанавливаются
обратные соотношения. Для облегчения
процесса принятия решения можно всякий
раз вычерчивать «ось значимости».
Критические
значения критерия обозначены как Qo,O5 и
Qo,O1> эмпирическое значение критерия
как QaMn. Оно заключено в эллипс.
Вправо
от критического значения Qo.oi простирается
«зона значимости» — сюда попадают
эмпирические значения, превышающие
Qooi и, следовательно, безусловно значимые.
Влево
от критического значения Qo,O5 простирается
«зона незначимое™», — сюда попадают
эмпирические значения Q, которые ниже
Qo,O5′ и≫
следовательно, безусловно незначимы.
Мы видим, что Qo,o5=6; Qo.oi=9; Q9Mn=8.
Эмпирическое
значение критерия попадает в область
между Qo,O5 и Qo.oi- Это зона «неопределенности»:
мы уже можем отклонить гипотезу о
недостоверности различий (HQ), НО еще не
можем принять гипотезы об их достоверности
(Hf).
Практически,
однако, исследователь может считать
достоверными уже те различия, которые
не попадают в зону незначимости, заявив,
что они достоверны при р<0,05, или указав
точный уровень значимости полученного
эмпирического значения критерия,
например: р=0,02. С помощью таблиц Приложения
1 это можно сделать по отношению к
критериям Н Крускала-Уоллиса, у}г
Фридмана,
L Пейджа, ф* Фишера, X
Колмогорова.
Уровень
статистической значимости или критические
значения критериев определяются
по-разному при проверке направленных
и ненаправленных статистических гипотез.
При направленной статистической гипотезе
используется односторонний критерий,
при ненаправленной гипотезе — двусторонний
критерий. Двусторонний критерий более
строг, поскольку он проверяет различия
в обе стороны, и поэтому то эмпирическое
значение критерия, которое ранее
соответствовало уровню значимости
р<0,05, теперь соответствует лишь уровню
р<0,10.
Билет 9 Параметрические
и непараметрические методы. Мощность
критериев
-
Параметрические и непараметрические
методы
Методы обучения, т.е. нахождения достаточно
хорошей распознающей функ-
ции f 2 F, традиционно подразделяются на
параметрические и непарамет-
рические в соответствии с тем, просто
или сложно устроено пространство F.
Параметрические — это те методы, в
которых F = fF(w; ¢)jw 2 Wg для неко-
торого достаточно удобного (например,
евклидова) пространства параметров
W и некоторой функции F: W £ X ! Y, а
непараметрические — это мето-
ды, в которых, якобы, пространство F не
зафиксировано заранее, а зависит
от обучающего набора T. На самом деле
разница между параметрическими и
непараметрическими методами — только
в употребляемых словах.
Полезный пример параметрических методов
— методы обучения линейных
распознавателей, которых даже для
простейшей линейной регрессии (X = Rd,
Y
= R,
W
= R
£ Rd,
F(w;
x)
= w0
+Pdj=1
wjxj) довольно много. Подробнее
эти методы рассматриваются в разделе
2.
[А.Б. Мерков]
непараметрические
методы в
математической статистике, методы
непосредственной оценки теоретического
распределения вероятностей и тех или
иных его общих свойств (симметрии и
т.п.) по результатам наблюдений. Название
Н. м. подчёркивает их отличие от
классических (параметрических)
методов, в которых
предполагается, что неизвестное
теоретическое распределение принадлежит
какому-либо семейству, зависящему от
конечного числа параметров (например,
семейству нормальных распределений, и
которые позволяют по результатам
наблюдений оценивать неизвестные
значения этих параметров и проверять
те или иные гипотезы относительно их
значений. Разработка Н. м. является в
значительной степени заслугой советских
учёных.
-
Мощность критериев
Мощность критерия — это его способность
выявлять различия, если они есть. Иными
словами, это его способность отклонить
нулевую гипотезу об отсутствии различий,
если
она неверна.
Ошибка, состоящая в том, что мы приняли
нулевую гипотезу, в то время как
она неверна, называется ошибкой II рода.
Вероятность такой ошибки обозначается
как β. Мощность критерия — это его
способность не допустить ошибку II рода,
поэтому:
Мощность=1—β
Мощность критерия определяется
эмпирическим путем. Одни и те же задачи
могут
быть решены с помощью разных критериев,
при этом обнаруживается, что некоторые
критерии позволяют выявить различия
там, где другие оказываются неспособными
это
сделать, или выявляют более высокий
уровень значимости различий. Возникает
вопрос: а
зачем же тогда использовать менее
мощные критерии? Дело в том, что
основанием для
выбора критерия может быть не только
мощность, но и другие его характеристики,
а
именно:
а) простота;
б) более широкий диапазон использования
(например, по отношению к данным,
определенным по номинативной шкале,
или по отношению к большим n);
в) применимость по отношению к неравным
по объему выборкам;
г) большая информативность результатов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Маркетинг – та сфера, где больше всего любят работать с большими данными (англ. big data), однако излюбленный инструмент маркетологов – A/B-тестирование – предполагает использование малых данных (англ. small data). При этом какие бы цифры ни были получены по итогам теста, все сводится к анализу статистической выборки и определению статистической значимости результатов эксперимента. Неотъемлемой частью данного исследования является P-значение, о котором мы хотим рассказать в этой статье.
Что такое P-значение
P-value или p-значение – одна из ключевых величин, используемых в статистике при тестировании гипотез. Она показывает вероятность получения наблюдаемых результатов при условии, что нулевая гипотеза верна, или вероятность ошибки в случае отклонения нулевой гипотезы.
Этот термин первым упомянул в своих работах К. А. Браунли в 1960 году. Он описал p-уровень значимости как показатель, который находится в обратной зависимости от истинности результатов. Чем выше р-value, тем ниже степень доверия в выборке зависимости между переменными.
Другими словами, в статистике p-значение – это наименьшее значение уровня значимости, при котором полученная проверочная статистика ведет к отказу от основной (нулевой) гипотезы.
Значение p-уровня чаще всего соответствует статистической значимости, равной 0,05. Если значение р меньше 0,05, нулевую гипотезу отклоняют. При этом чем меньше это значение, тем лучше, т. к. растет предполагаемая значимость альтернативной гипотезы и «сила» отвержения нулевой.
Часто p-значение понимают неправильно. Например, если значение р = 0,05, можно сказать о том, что существует 5% вероятности, что результат получен случайно и не соответствует действительности.

Кратко о главном
- Р-значение показывает вероятность того, что наблюдаемая разница в результатах могла быть случайной.
- Значение p применяется как альтернатива выбранным уровням достоверности для тестирования идей или в дополнение к ним.
- Со снижением p-значения повышается статистическая значимость разницы, полученной в ходе исследования.
Статистическая значимость
Эксперимент начинается с формулирования нулевой гипотезы. Она показывает, что два исследуемых явления никаким образом не связаны друг с другом.
Эксперимент проводится с целью выявить или показать какое-либо влияние или тип взаимодействия рассматриваемых явлений. Если в итоге анализа подтверждается нулевая гипотеза, значит, тест провалился.
Чтобы правильно интерпретировать результаты, рассчитывают показатель статистической значимости.
Статистическая значимость – это критерий, с помощью которого можно определить, необходимо ли отвергнуть или принять ту или иную гипотезу.
Перед началом тестирования следует установить порог значимости (альфа). Если значение р меньше альфа, можно говорить о том, что наш результат является статистически значимым. Это говорит о том, что наблюдаемое явление действительно имело место, и нулевую гипотезу нужно отклонить.
Порог значимости альфа устанавливается обычно на уровне 0,05 или 0,01. Выбор значения определяется поставленной задачей.
Порог значимости равен 0,05, а p-значение – 0,02. Т. к. установленное значение альфа больше p-уровня, делаем вывод, что это статистически значимый результат.
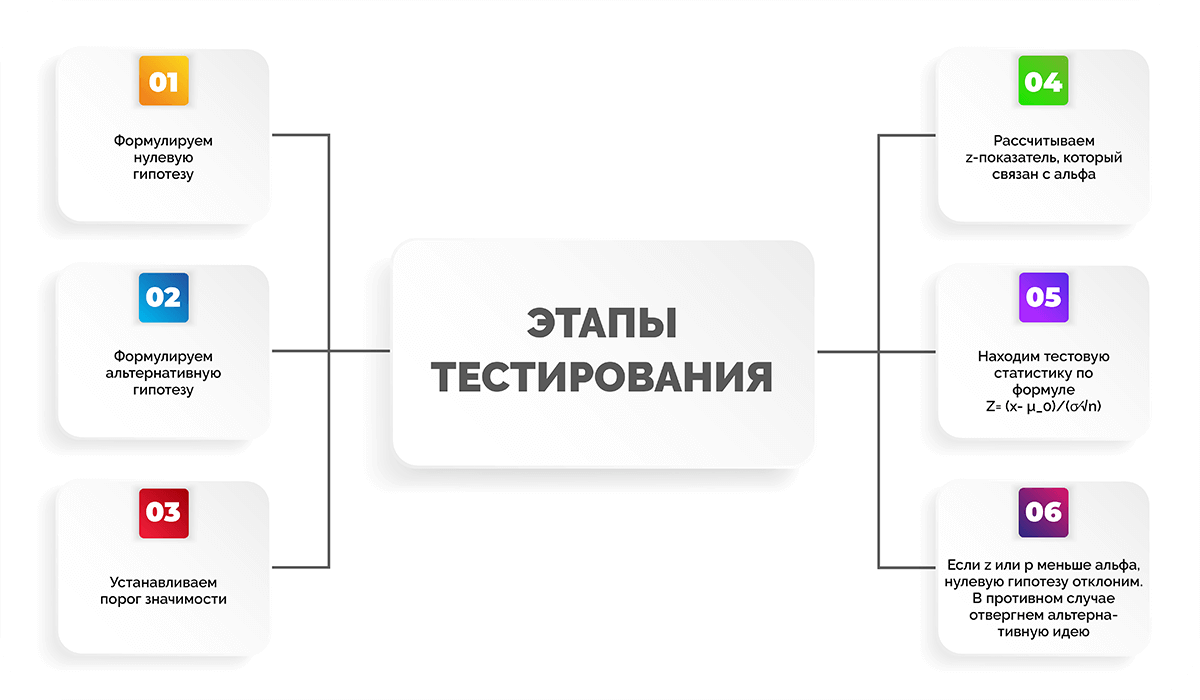
Все тестирование можно разделить на несколько этапов:
- Формулируем нулевую гипотезу.
- Формулируем альтернативную гипотезу.
- Устанавливаем порог значимости.
- Рассчитываем z-показатель, который связан с альфа.
- Находим тестовую статистику по формуле
.
- Если z-показатель или p-значение меньше уровня альфа, нулевую гипотезу отклоним. В противном случае отвергнем альтернативную идею.
Если идет речь о явлениях, которые управляются случайными процессами, обычно это приводит к нормальному распределению значений. В этом случае нулевую гипотезу представляют в виде кривой Гаусса, которая отражает распределение ожидаемых наблюдений. Это распределение актуально в случае, если одна переменная в эксперименте не зависит от другой.
Порог вероятности
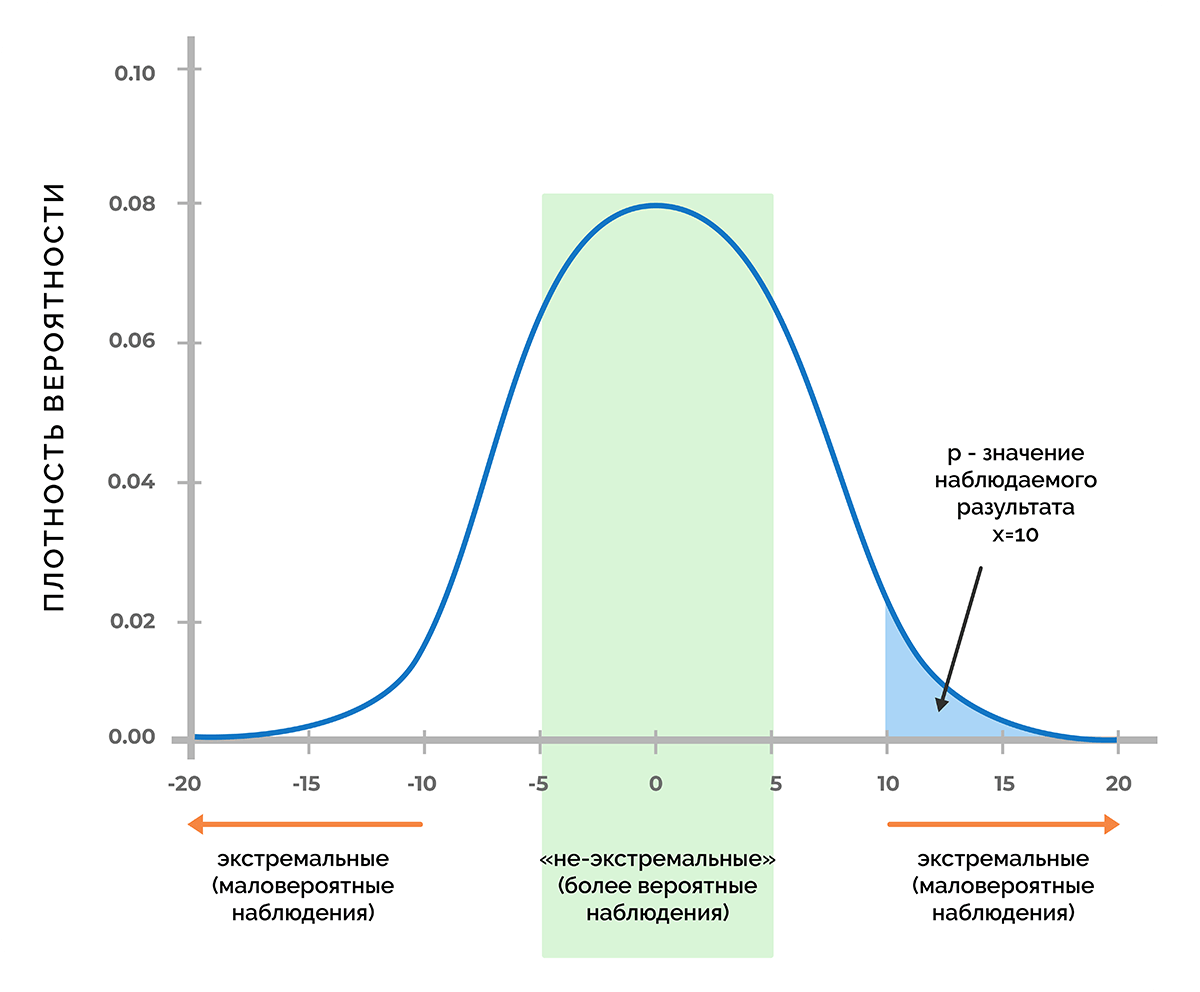
В основе статистической значимости лежит вероятность получения определенного результата при верности нулевой гипотезы. Чтобы разобрать смысл этого определения, предположим, что в процессе тестирования получили некое число х. Это может быть любая метрика, например, прибыль от продаж, величина конверсии, количество довольных покупателей и т. д.
Используя функцию плотности вероятности, которая связана с нулевой гипотезой, можно выяснить, удастся ли получить число х (или любое другое значение, которое маловероятнее, чем х) с вероятностью менее 5% (p < 0,05) или менее 1% (p < 0,01), или другого порога, при котором p меньше заданного уровня значимости.
Таким образом, p-критерий отражает вероятность получения результата, который равен или является более экстремальным, чем фактически наблюдаемый результат, в случае отсутствия взаимосвязи между исследуемыми переменными.
Доверительные уровни
Доверительный уровень значимости выбирается перед запуском статистического эксперимента. Чаще всего используются значения 90%, 95% или 99%.
Ниже в таблице приводим критические p-значения, а также z-оценки для разных доверительных уровней.
|
Доверительный уровень |
Стандартное отклонение (z-оценка) |
Вероятность (p-уровень) |
|
90% |
< -1,65 или > +1,65 |
< 0,10 |
|
95% |
< -1,96 или > +1,96 |
< 0,05 |
|
99% |
< -2,58 или > +2,58 |
< 0,01 |
Значения, которые находятся в пределах области нормального распределения z-оценки (стандартного отклонения), представляют ожидаемый результат.
Проверка статистических гипотез
Проверка гипотезы – это статистическое исследование, которое проводится, чтобы подтвердить или опровергнуть какую-либо гипотезу (простую или сложную).
Можно предположить, что посадочная страница с красной кнопкой CTA даст больше конверсий, чем текущая версия лендинга с синей. Проверить это можно путем тестирования, в котором будут участвовать нулевая и альтернативная гипотезы.
Нулевая гипотеза – первоначальное условие, при котором нет никакой разницы между текущей и новой версиями лендинга в плане конверсии
Альтернативная гипотеза – подразумевает, что изменение цвета кнопки на странице является причиной роста конверсии.
В статистике применяется рандомизация и нормализация нулевой гипотезы.
Рандомизация нулевой гипотезы – пространственная модель данных, которую мы наблюдаем, является одним из многих вариантов пространственных организаций данных. При этом все другие варианты не будут заметно отличаться от наблюдаемых.
Нормализация нулевой гипотезы подразумевает, что наблюдаемые значения являются одним из многих случайных вариантов выборок. При этом ни пространственное расположение данных, ни их значения не установлены.
Благодаря значению p можно увидеть, насколько нулевая гипотеза правдоподобна с учетом данных выборки. Таким образом, если нулевая гипотеза подтвердится, p-значение будет свидетельствовать об отсутствии увеличения конверсии вследствие изменения цвета кнопки.
Подход p-value к проверке гипотез
Значение р может использоваться для выявления доказательства для отклонения нулевой (первоначальной) гипотезы в ходе эксперимента.
Мы уже упоминали выше о том, что уровень значимости обозначается до начала исследования, чтобы определить, насколько малое значение p нужно получить для опровержения нулевой гипотезы. Однако в разных случаях разные люди могут использовать разные уровни значимости, поэтому при интерпретации итогов двух разных тестирований другими людьми могут возникать трудности. Решить эту проблему помогает p-value.
Рассмотрим пример, в котором в компании провели исследование, в ходе него сравнили доходность двух активов. Тест и анализ проводили два специалиста, которые брали за основу одни и те же самые исходные данные, но использовали разные уровни значимости. Есть вероятность, что эти люди сделают противоположные выводы о различии активов. Предположим, что один специалист для отклонения нулевой гипотезы взял уровень достоверности 90%, а другой – 95%. При этом среднее значение p наблюдаемой разницы между результатами равнялось 0,08, что отвечает уровню достоверности 92%. В таком случае первый специалист выявит значимое различие между двумя доходами, а второй статистически значимой разницы не обнаружит.
Чтобы избежать подобной ситуации, можно сообщить значение p-value эксперимента и дать возможность независимым наблюдателям самостоятельно оценивать статистическую значимость итоговых данных. Данный подход к проверке утверждений стали называть «подход p-value».
Как рассчитать P-value
Чаще всего p-значения определяют с помощью таблиц p-value или специализированного статистического ПО. Также помогает в этом калькулятор на тематических сайтах. Подобные расчеты основываются на известном или предполагаемом распределении вероятностей определенной статистики. Определение среднего значения р зависит от отклонения между выбранным эталонным и тестовым значением. При этом учитывается нормальное распределение вероятностей статистики.
Что касается ручного математического расчета значения р, существуют разные способы, которые рассмотрим далее в статье.
Как рассчитать p-значение, используя тестовую статистику
Распределение тестовой статистики происходит с предполагаемым условием, что верна нулевая гипотеза. Чтобы выразить вероятность того, что статистика эксперимента будет такой же экстремальной, как значение x для выборки, используется кумулятивная функция распределения.
Левосторонний эксперимент:
P-value = cdf (x)
Правосторонний эксперимент:
P-value = 1 – cdf (x)
Двусторонний эксперимент:
P-value = 2 × мин {{cdf (x), 1 – cdf (x)}}
Ручной расчет значения p затрудняют распространенные распределения вероятностей, которыми характеризуется проверка гипотез. Для расчета примерных показателей cdf удобнее использовать статистическую таблицу или ПК.
Пошаговый алгоритм расчета p-значения
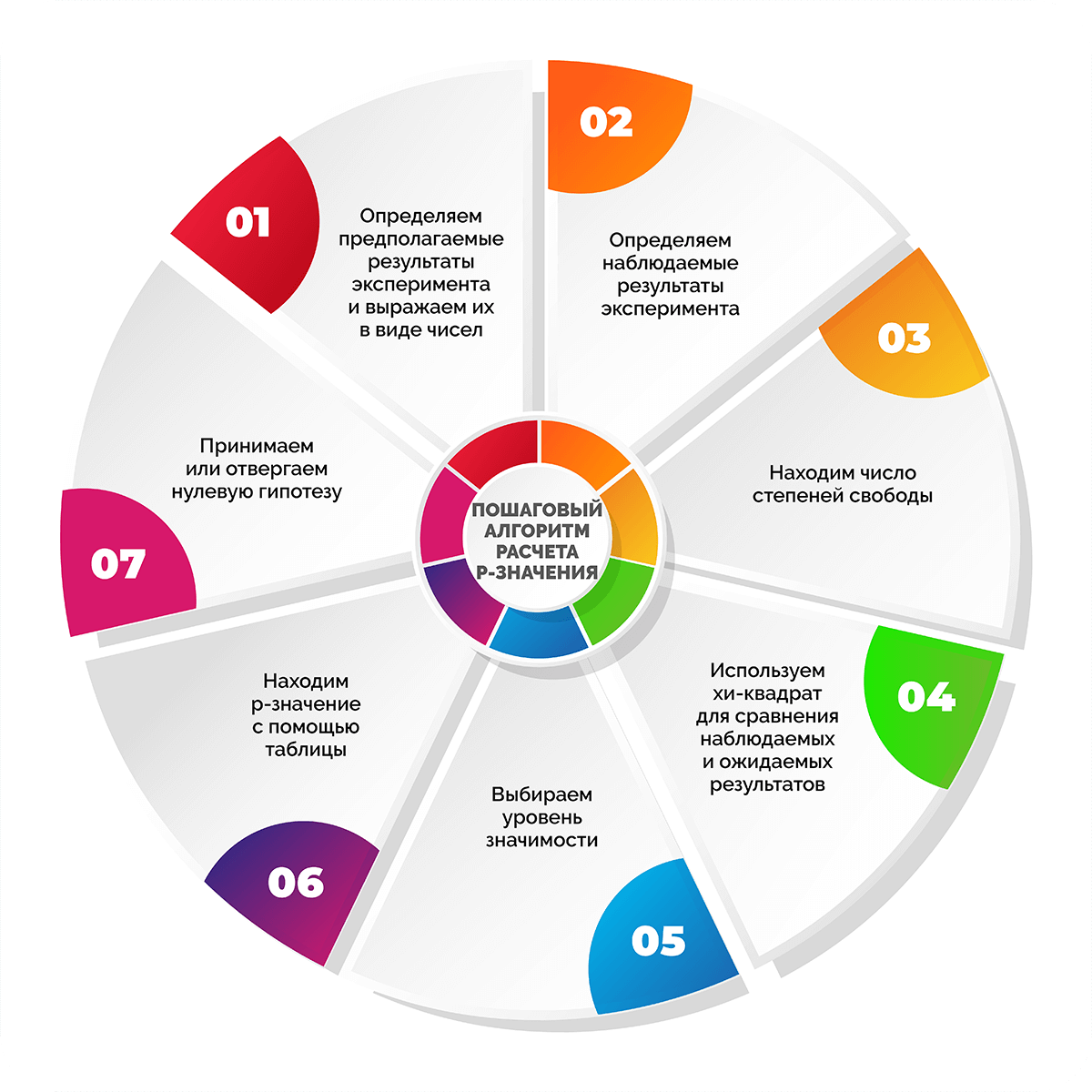
Шаг 1. Определяем предполагаемые результаты эксперимента и выражаем их в виде чисел
Как правило, на начало исследования уже есть видение того, какие числа можно считать приемлемыми. Выводы могут быть основаны на опыте проведения предыдущих экспериментов, наборах достоверных данных или общих сведеньях из научной литературы и других источников.
Опыт работы с лендингами показывает, что посадочные страницы с CTA-кнопкой на первом экране приводят примерно вдвое больше покупателей, чем версии без таких кнопок. Необходимо определить, действительно ли наличие кнопки влияет на посетителей сайта. Для этого будем анализировать конверсии в покупку. Если взять условные 300 конверсий, то предполагается, что 200 из них произойдут благодаря лендингам с CTA-кнопкой, а 100 – сайтам без кнопки при условии, что пользователи требовательны к наличию кнопок.
Шаг 2. Определяем наблюдаемые результаты эксперимента
Теперь нужно провести тест и получить реальные, т. е. наблюдаемые значения, которые таже будут выражаться в числовом формате. Если в экспериментальных условиях реальные цифры не совпадут с ожидаемыми, то будет два варианта – или это обусловлено действиями в ходе эксперимента, или получилось случайно. В данном случае цель определения p-value – понять, действительно ли наблюдаемые значения отличаются от ожидаемых настолько, что нулевая гипотеза не будет опровергнута.
Предположим, что мы выбрали 300 случайных конверсий с наших сайтов, на которых либо была кнопка на первом экране, либо ее не было. Определили, что 220 конверсий произошли благодаря лендингам с кнопкой и 80 – без нее. Результаты отличаются от ожидаемых, которые составляли 200 и 100 соответственно. Теперь предстоит узнать, действительно ли к изменению в значениях привел наш тест (добавление кнопки на первый экран) или это случайное отклонение. Определить это поможет p-значение.
Шаг 3. Находим число степеней свободы
Число степеней свободы показывает, насколько может измениться эксперимент. При этом степень изменяемости зависит от количества исследуемых категорий.
Число степеней свободы = n – 1, где n – количество анализируемых переменных или категорий.
В нашем эксперименте 2 условия и, соответственно, две категории результатов: для лендингов без кнопки на первом экране и для лендингов с ней.
Число степеней свободы = 2 – 1 = 1.
Если бы в эксперименте мы сравнивали посадочные станицы с CTA-кнопкой, без кнопки и с pop-up окном, то получили бы 2 степени свободы и т. д.
Шаг 4. Используем хи-квадрат для сравнения наблюдаемых и ожидаемых результатов
Хи-квадрат (х2) – числовое отражение разницы между наблюдаемыми (фактическими) и ожидаемыми значениями тестирования.
где:
о – наблюдаемое значение;
е – ожидаемое значение.
Подставляем наши цифры в уравнение и учитываем, что 
х2 = ((220 – 200)2/200) + ((80 – 100)2/100) = ((20)2/200)) + ((-20)2/100) = (400/200) + (400/100) = 2 + 4 = 6.
Шаг 5. Выбираем уровень значимости
Уровень значимости отражает степень уверенности в полученных результатах. Если статистическая значимость низкая, это говорит о низкой вероятности случайного получения экспериментальных результатов.
Для большинства тестов достаточно статистической значимости, равной 0,05 или 5%. При этом будет вероятность 95%, что исследователь получил значимый результат вследствие проведенных мероприятий, а не случайно.
В нашем случае примем статистическую значимость, равную 0,05.
Шаг 6. Находим p-значение с помощью таблицы
Для облегчения расчетов статисты применяют специализированные таблицы. Они довольно простые и позволяют легко найти значение р, зная число степеней свободы и хи-значение. Слева по вертикали располагаются значения числа степеней свободы. Вверху по горизонтали находятся p-значения. По данным таблицы сначала находят нужное число степеней свободы, затем в соответствующем ему ряду выбирают первое значение, которое превышает расчетное значение хи-квадрата. Число в верхней горизонтальной строке будет соответствовать p-значению. При этом нужное значение р находится в диапазоне чисел между найденным и следующим за ним слева.
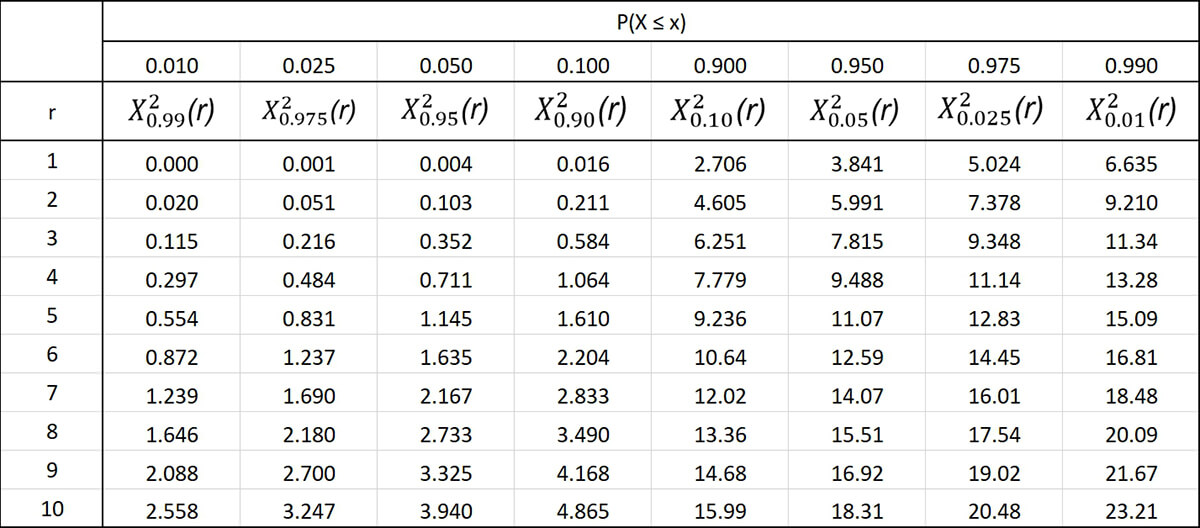
В нашем примере всего одна степень свободы, а хи-квадрат равен 6. Поэтому в таблице выбираем первую строку и движемся по ней слева направо до тех пор, пока не увидим первое значение больше 6 – это число 6,635. Оно соответствует p-значению 0,01, а значит, наше p-значение находится в диапазоне между 0,01 и 0,025.
Шаг 7. Принимаем или отвергаем нулевую гипотезу
Если найденное приблизительное значение p меньше уровня значимости, можно заключить, что вероятна связь между экспериментальными переменными и полученными результатами. В противном случае нельзя утверждать с уверенностью, связаны ли результаты с манипуляцией переменными или стали случайностью.
В нашем эксперименте диапазон значений р 0,01-0,025 определенно меньше установленной статистической значимости 0,05, что позволяет отклонить нулевую гипотезу. А значит, можно сделать вывод, что посадочные страницы с CTA-кнопкой на 1-м экране конвертируют лучше, чем аналогичные версии без такой кнопки. Вероятность того, что рост конверсий на лендингах с кнопкой является случайностью, составляет не больше 1-2,5%.
Как интерпретировать P-значение
P-уровень тесно связан с уровнем статистической значимости. Последний таже определяет исход эксперимента.
- Если p-значение меньше уровня значимости, то нулевую гипотезу можно смело отклонить и считать истинной альтернативную гипотезу.
- Если p-значение больше уровня значимости, это означает, что в ходе эксперимента выявили недостаточно оснований для отклонения нулевой гипотезы.
Отвержение нулевой гипотезы говорит о том, что в процессе исследования была обнаружена закономерная связь между тестируемыми переменными.
P-значение – это…
- вероятность того, что в ходе исследования наблюдения были случайными. То есть, если p = 0,05, есть 5% вероятности того, что наблюдаемое явление случайно и 95% вероятности того, что результат является следствием созданных условий;
- вероятность того, что будет сделан неверный вывод о взаимосвязи переменных. Если р = 0,05, то на каждые 100 экспериментов, где наблюдалась взаимосвязь, 95 их них действительно была, а 5 – нет.
Что нужно помнить о P-значениях
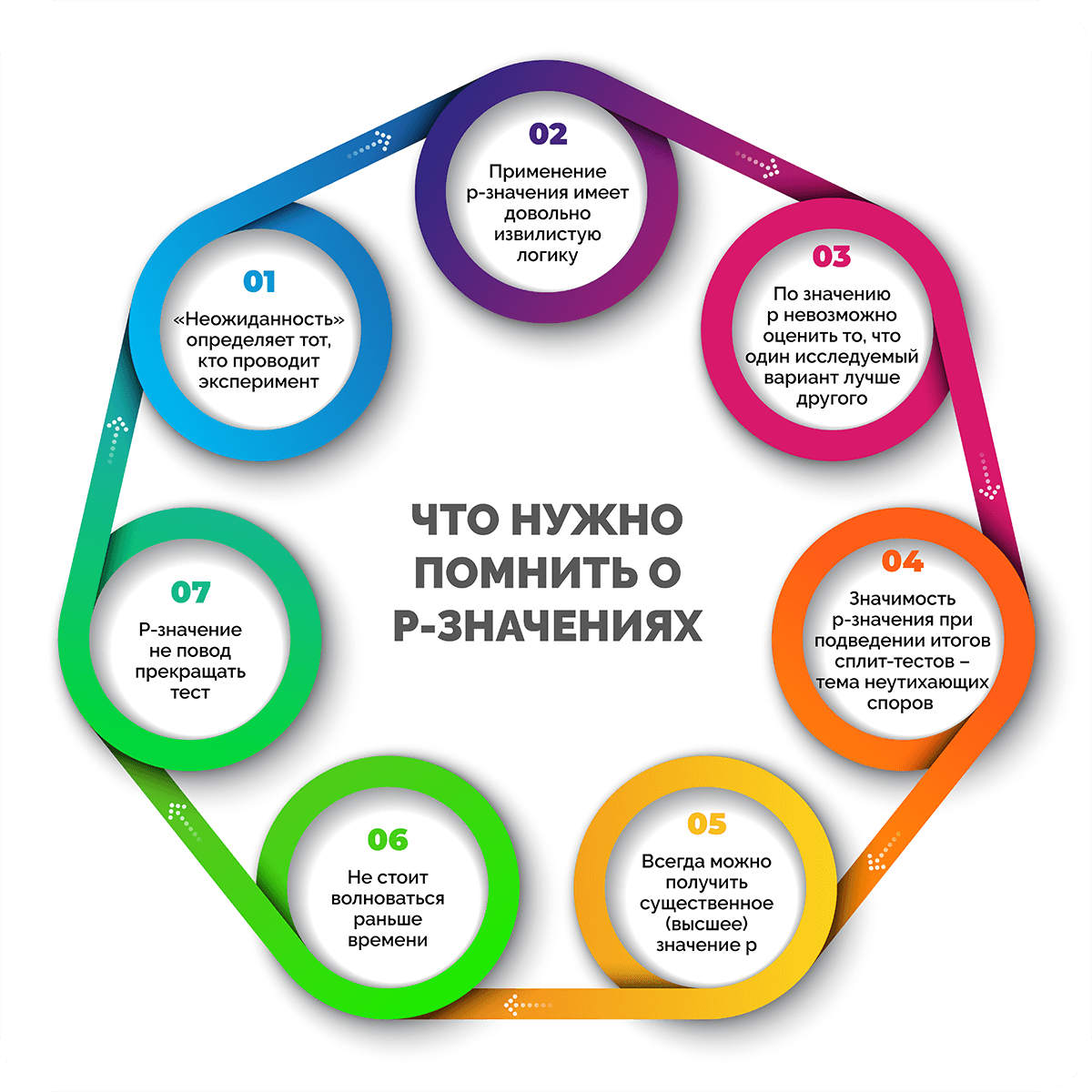
- «Неожиданность» определяет тот, кто проводит эксперимент. Подводит итоги теста по факту тот, кто его проводит. Чем выше значение р, тем чаще вы будете получать неожиданные результаты.
- Применение p-значения имеет довольно извилистую логику. Чтобы оценить аргументы в пользу отклонения нулевой гипотезы, необходимо изначально считать, что она верна. Именно это является причиной путаницы.
- По значению p невозможно оценить вероятность того, что один исследуемый вариант лучше другого. Также по этому показателю нельзя понять, какая вероятность того, что предпочтение одного варианта другому ошибочно. На самом деле, p-значение показывает лишь вероятность того, что при верности нулевой гипотезы удастся вычислить результат, отличный от нуля.
- Значимость p-значения при подведении итогов сплит-тестов – тема неутихающих споров в научном сообществе. Большинство маркетологов остаются приверженцами классической проверки на статистическую значимость и отстаивают ее как «золотой стандарт». При этом специалисты по статистике приводят аргументы в пользу других методов проверки, что провоцирует жаркие дебаты.
- Всегда можно получить существенное (высшее) значение p. Есть типичная ошибка, которая зависит с одной стороны от объема выборки, с другой – от изменений генеральной совокупности данных. Если во втором случае повлиять на изменения никак нельзя, то собирать и накапливать данные ничто не мешает. Но есть ли польза от такого количества сведений? Сам факт того, что у полученного параметра высокое p-значение, практического значения не имеет.
- Не стоит волноваться раньше времени. В первую очередь нужно собрать данные, которые помогут сформировать рабочую идею. Всегда трудно делать выбор между вариантами, которые почти не отличаются друг от друга. Если выделить предпочтительный вариант проблематично из-за похожих результатов, можно просто выбрать один из них и не беспокоиться о том, правильный ли это выбор.
- P-значение не повод прекращать тест. Для получения достоверных результатов, которые позволят интерпретировать p-значение, необходимо вычислить размер выборки, затем провести эксперимент. В процессе тестирования предстоит выбрать время, когда пора его закончить. При этом оно не должно быть связано с достижением статистической значимости или высокого показателя p-значения. Главное – получить реальные результаты в конце теста, например, обеспечить рост прибыли, оптимизировать конверсию и т. д.
Примеры интерпретации P-значений
На нескольких примерах рассмотрим, как правильно интерпретировать p-значения при проверке разных идей.
По мнению интернет-провайдера, 90% пользователей довольны качеством предоставляемых услуг. Чтобы это проверить, была собрана простая выборка, куда вошли 500 случайных абонентов. 85% дали утвердительный ответ на вопрос об удовлетворенности услугами провайдера. По данным выборки удалось вычислить p-значение, равное 0,018.
Если выдвинуть гипотезу о том, что 90% пользователей действительно довольны обслуживанием провайдера, получим реальную наблюдаемую разницу или более экстремальную разницу, которая составит 1,8% потребителей услуг вследствие ошибки случайной выборки.
Ресторан вводит услугу доставки еды и утверждает, что время доставки составляет около 30 минут или меньше. Однако есть мнение, что реальный срок доставки превышает заявленное время. Для проверки этих вариантов были отобраны случайные заказы еды с доставкой и проведены расчеты. По результатам выяснили, что среднее время доставки составляет 40 минут (больше на 10 минут, чем заявляет ресторан), а p-значение равно 0,03.
Результаты показывают, что в случае, когда нулевая гипотеза верна, т. е. доставка еды занимает 30 минут или меньше, есть вероятность 3%, что среднее время доставки будет как минимум на 10 минут больше из-за эффекта случайности.
Отдел маркетинга разрабатывает новый скрипт продаж для менеджеров. Предполагается, что с его помощью компания будет продавать минимум на 30% больше, чем со старым скриптом. Чтобы это проверить, собирается простая случайная выборка из 100 контактов с клиентами по новому скрипту и 100 – по старому. В результате эксперимента новый скрипт привел 60 покупателей, а старый – 45. Вычислили среднее значение p, равное 0,011.
Если взять за основу мнение, что новый скрипт приводит столько же клиентов, сколько и старый, или меньше, будет получена крайняя разница в 1,1% тестирований вследствие случайной ошибки выборки.
Часто задаваемые вопросы
P-значение – вероятность того, что исследуемая статистика удовлетворит конкретным условиям. Поскольку вероятности отрицательными не бывают, отрицательного значения p тоже быть не может.
Если p-значение высокое, это свидетельствует о том, что статистика эксперимента для другой выборки будет иметь столь же экстремальное значение, как и в тестируемой выборке. При высоком p-значении отвергнуть нулевую гипотезу нельзя.
Если получено низкое p-значение, это значит, что вероятность получить такое же критическое значение, как и наблюдаемое в текущей выборке, в тестовой статистике для другой выборки окажется очень низкой. При низком p-значении нулевую гипотезу отвергают и принимают альтернативную.
Некоторые считают, что p-значения показывают вероятность совершить ошибку при отклонении истинной нулевой гипотезы (ошибка первого типа) – это заблуждение. P-значения не свидетельствуют о частоте вероятных ошибок по двум причинам:
- При расчете p-значения в основе утверждение, что верна нулевая гипотеза, а разница в итоговых данных обусловлена случайностью. То есть величина p-значения не отражает вероятность того, что ноль будет ложным или истинным, т. к. с учетом изначального предположения он полностью верен.
- Несмотря на то, что при низком p-значении при условии истинности нулевого значения выборочные данные маловероятны, p-значение все еще не может четко показать, какой из вариантов имеет большую вероятность стать истиной: когда нуль действительно является ложным или когда нуль является верным, но выборка нечеткая.
Заключение
Несмотря на то, что при интерпретации результатов исследований часто допускают ошибки, неправильно используя статистическую значимость, она продолжает оставаться важным методом в экспериментах. P-значение или p-value является одной из обязательных составляющих при оценке результатов тестирования. Именно этот показатель дает возможность понять, с какой вероятностью полученные итоги удовлетворяют определенным значениям.
Олег Вершинин
Специалист по продукту
Все статьи автора
Нашли ошибку в тексте? Выделите нужный фрагмент и нажмите
ctrl
+
enter
| Часть серии по статистике |
| Теория вероятности |
|---|
 |
|
|
|
|
|
|
Попарная вероятность ошибки есть вероятность ошибки , что для передаваемого сигнала ( ) , соответствующая ее , но искаженная версия ( ) будет получена. Этот тип вероятности называется «парной вероятностью ошибки», потому что вероятность существует с парой векторов сигналов в сигнальном созвездии. В основном используется в системах связи.
Расширение определения
Как правило, принятый сигнал представляет собой искаженную версию переданного сигнала. Таким образом, мы вводим вероятность ошибки символа, которая представляет собой вероятность того, что демодулятор сделает неправильную оценку переданного символа на основе принятого символа, которая определяется следующим образом:
где M — размер сигнального созвездия.
Вероятность попарной ошибки определяется как вероятность того, что при передаче будет получено.
-
может быть выражена как вероятность того, что по крайней мере один ближе , чем к .
Используя верхнюю границу вероятности объединения событий, можно записать:
В заключение:
Вычисление в закрытой форме
Для простого случая канала аддитивного белого гауссова шума (AWGN):
В закрытом виде PEP можно рассчитать следующим образом:

Для нулевого среднего, дисперсия гауссовской случайной величины:
Следовательно,
Смотрите также
- Обработка сигналов
- Телекоммуникации
- Электротехника
- Случайная переменная
Ссылки
дальнейшее чтение
- Прасад, 5-й международный симпозиум IEEE по персональной, внутренней и мобильной радиосвязи (PIMRC ’94), Гаага, Нидерланды, 18–22 сентября 1994 г .; Региональное совещание ICCC по беспроводным компьютерным сетям (WCN), Гаага, Нидерланды, 21–23 сентября 1994 г .; под редакцией Джоса Х. Вебера, Йенса К. Арнбака и Рамджи (1994). Беспроводные сети: ловя мобильное будущее: труды . Амстердам: IOS Press. С. 564–575. ISBN 9051991932.
- Саймон, Марвин К .; Алуини, Мохамед-Слим (2005). Цифровая связь по каналам с замиранием (2-е изд.). Хобокен: Джон Уайли и сыновья. ISBN 0471715239.
Статистические символы
Таблица и определения символов вероятности и статистики.
Таблица вероятностных и статистических символов
| Символ | Название символа | Значение / определение | пример |
|---|---|---|---|
| P ( А ) | функция вероятности | вероятность события A | P ( A ) = 0,5 |
| P ( A ∩ B ) | вероятность пересечения событий | вероятность того, что событий A и B | P ( A ∩ B ) = 0,5 |
| P ( A ∪ B ) | вероятность объединения событий | вероятность того, что событий A или B | P ( A ∪ B ) = 0,5 |
| P ( A | B ) | функция условной вероятности | вероятность события A данное событие B произошло | P ( A | B ) = 0,3 |
| f ( x ) | функция плотности вероятности (pdf) | P ( a ≤ x ≤ b ) = ∫ f ( x ) dx | |
| F ( х ) | кумулятивная функция распределения (cdf) | F ( х ) = Р ( Х ≤ х ) | |
| μ | Средняя численность населения | среднее значение совокупности | μ = 10 |
| E ( X ) | ожидаемое значение | ожидаемое значение случайной величины X | E ( X ) = 10 |
| E ( X | Y ) | условное ожидание | ожидаемое значение случайной величины X с учетом Y | E ( X | Y = 2 ) = 5 |
| var ( X ) | отклонение | дисперсия случайной величины X | var ( X ) = 4 |
| σ 2 | отклонение | дисперсия значений совокупности | σ 2 = 4 |
| std ( X ) | стандартное отклонение | стандартное отклонение случайной величины X | std ( X ) = 2 |
| σ X | стандартное отклонение | значение стандартного отклонения случайной величины X | σ X = 2 |
| медиана | среднее значение случайной величины x | ||
| cov ( X , Y ) | ковариация | ковариация случайных величин X и Y | cov ( X, Y ) = 4 |
| корр ( X , Y ) | корреляция | корреляция случайных величин X и Y | корр ( X, Y ) = 0,6 |
| ρ X , Y | корреляция | корреляция случайных величин X и Y | ρ X , Y = 0,6 |
| ∑ | суммирование | суммирование — сумма всех значений в диапазоне ряда | |
| ∑∑ | двойное суммирование | двойное суммирование | |
| Пн | Режим | значение, которое чаще всего встречается в популяции | |
| MR | средний диапазон | MR = ( х макс + х мин ) / 2 | |
| Мкр | медиана выборки | половина населения ниже этого значения | |
| Q 1 | нижний / первый квартиль | 25% населения ниже этого значения | |
| 2 квартал | медиана / второй квартиль | 50% населения ниже этого значения = медиана выборки | |
| 3 квартал | верхний / третий квартиль | 75% населения ниже этого значения | |
| х | выборочное среднее | среднее / среднее арифметическое | х = (2 + 5 + 9) / 3 = 5,333 |
| с 2 | выборочная дисперсия | оценщик дисперсии выборки населения | s 2 = 4 |
| с | стандартное отклонение выборки | Оценка стандартного отклонения выборки населения | s = 2 |
| z x | стандартная оценка | z x = ( x — x ) / s x | |
| X ~ | распределение X | распределение случайной величины X | X ~ N (0,3) |
| N ( μ , σ 2 ) | нормальное распределение | гауссово распределение | X ~ N (0,3) |
| U ( а , б ) | равномерное распределение | равная вероятность в диапазоне a, b | Х ~ U (0,3) |
| ехр (λ) | экспоненциальное распределение | f ( x ) = λe — λx , x ≥0 | |
| гамма ( c , λ) | гамма-распределение | f ( x ) = λ cx c-1 e — λx / Γ ( c ), x ≥0 | |
| χ 2 ( к ) | распределение хи-квадрат | f ( x ) = x k / 2-1 e — x / 2 / (2 k / 2 Γ ( k / 2)) | |
| F ( k 1 , k 2 ) | F распределение | ||
| Корзина ( n , p ) | биномиальное распределение | f ( k ) = n C k p k (1 -p ) nk | |
| Пуассон (λ) | распределение Пуассона | е ( К ) знак равно λ К е — λ / К ! | |
| Геом ( p ) | геометрическое распределение | f ( k ) = p (1 -p ) k | |
| HG ( N , K , n ) | гипергеометрическое распределение | ||
| Берн ( p ) | Распределение Бернулли |
Комбинаторические символы
| Символ | Название символа | Значение / определение | пример |
|---|---|---|---|
| п ! | факториал | п ! = 1⋅2⋅3⋅ … ⋅ n | 5! = 1⋅2⋅3⋅4⋅5 = 120 |
| n P k | перестановка | 5 п 3 = 5! / (5-3)! = 60 | |
| n C k
|
сочетание | 5 C 3 = 5! / [3! (5-3)!] = 10 |
Установить символы ►
Смотрите также
- Математические символы
- Установить символы
- Основные математические символы
- Логические символы
- Символы греческого алфавита
- Распределение вероятностей
- Вероятность и статистика
Тип кодирования данных
Фазовая манипуляция (PSK ) — это цифровая модуляция процесс, который передает данные путем изменения (модуляции) фазы постоянного частоты эталонного сигнала ( несущая ). Модуляция осуществляется путем изменения входных сигналов синус и косинус в точное время. Он широко используется для беспроводных локальных сетей, RFID и Bluetooth связи.
Любая схема цифровой модуляции использует конечное количество различных сигналов для представления цифровых данных. PSK использует конечное количество фаз, каждой из которых назначен уникальный шаблон из двоичных цифр. Обычно каждая фаза кодирует равное количество битов. Каждый набор битов образует символ , который представлен конкретной фазой. Демодулятор , который разработан специально для набора символов, используемого модулятором, определяет фазу принятого сигнала и отображает ее обратно в символ, который он представляет, таким образом восстанавливая исходные данные. Для этого приемник должен иметь возможность сравнивать фазу принятого сигнала с опорным сигналом — такая система называется когерентной (и упоминается как CPSK).
CPSK требует сложного демодулятора, поскольку он должен извлекать опорную волну из принятого сигнала и отслеживать ее, чтобы сравнивать каждую выборку. В качестве альтернативы, фазовый сдвиг каждого отправленного символа можно измерить относительно фазы предыдущего отправленного символа. Поскольку символы кодируются с разностью фаз между последовательными выборками, это называется дифференциальной фазовой манипуляцией (DPSK) . DPSK может быть значительно проще в реализации, чем обычный PSK, поскольку это «некогерентная» схема, то есть демодулятору не нужно отслеживать опорную волну. Компромисс в том, что он имеет больше ошибок демодуляции.
Содержание
- 1 Введение
- 1.1 Определения
- 2 Приложения
- 3 Двоичная фазовая манипуляция (BPSK)
- 3.1 Реализация
- 3.2 Частота битовых ошибок
- 4 Квадратурная фаза- Shift-манипуляция (QPSK)
- 4.1 Реализация
- 4.2 Вероятность ошибки
- 4.3 Варианты
- 4.3.1 Смещение QPSK (OQPSK)
- 4.3.2 SOQPSK
- 4.3.3 π / 4- QPSK
- 4.3.4 DPQPSK
- 5 PSK высшего порядка
- 5.1 Частота битовых ошибок
- 5.2 Спектральная эффективность
- 6 Дифференциальная фазовая манипуляция (DPSK)
- 6.1 Дифференциальное кодирование
- 6.2 Демодуляция
- 6.3 Пример: дифференциально-кодированная BPSK
- 7 Взаимная информация с аддитивным белым гауссовским шумом
- 8 См. Также
- 9 Примечания
- 10 Ссылки
Введение
Есть три основных класса методов цифровой модуляции, используемых для передачи представленных в цифровом виде данных:
Все передают данные, изменяя какой-либо аспект основного знака al, несущая (обычно синусоида ) в ответ на сигнал данных. В случае PSK фаза изменяется для представления сигнала данных. Существует два основных способа использования фазы сигнала таким образом:
- путем рассмотрения самой фазы как передачи информации, и в этом случае демодулятор должен иметь опорный сигнал. сигнал для сравнения фазы принятого сигнала; или
- При просмотре изменения в фазе, как транспортирующая информация -. дифференциального схема, некоторые из которых не нужен опорный носителя (в определенную степень)
Удобный способ представления схем PSK — это диаграмма созвездия . Здесь показаны точки на комплексной плоскости , где в данном контексте оси действительная и мнимая называются синфазной и квадратурной осями соответственно из-за их Разделение на 90 °. Такое представление на перпендикулярных осях легко реализуется. Амплитуда каждой точки вдоль синфазной оси используется для модуляции косинусной (или синусоидальной) волны, а амплитуда вдоль квадратурной оси — для модуляции синусоидальной (или косинусной) волны. По соглашению синфазная модуляция модулирует косинус, а квадратурная модуляция синуса.
В PSK выбранные точки созвездия обычно располагаются с равномерным угловым интервалом вокруг окружности. Это обеспечивает максимальное разделение фаз между соседними точками и, следовательно, лучшую защиту от повреждений. Они расположены по кругу, поэтому все они могут передаваться с одинаковой энергией. Таким образом, модули комплексных чисел, которые они представляют, будут такими же, как и амплитуды, необходимые для косинусной и синусоидальной волн. Двумя распространенными примерами являются «двоичная фазовая манипуляция» (BPSK), которая использует две фазы, и «квадратурная фазовая манипуляция» (QPSK), которая использует четыре фазы, хотя любое количество фаз могут быть использованы. Поскольку данные, которые должны быть переданы, обычно являются двоичными, схема PSK обычно разрабатывается с количеством точек совокупности, равным степени двух.
Определения
Для математического определения частоты ошибок потребуются некоторые определения:
Q (x) { displaystyle Q (x)}

- Q (x) = 1 2 π ∫ x ∞ e — 1 2 t 2 dt = 1 2 erfc (x 2), x ≥ 0 { displaystyle Q (x) = { frac {1} { sqrt {2 pi}}} int _ {x} ^ { infty} e ^ {- { frac {1} {2}} t ^ { 2}} , dt = { frac {1} {2}} operatorname {erfc} left ({ frac {x} { sqrt {2}}} right), x geq 0}
.
Приведенные здесь коэффициенты ошибок соответствуют аддитивному белому гауссовскому шуму (AWGN). Эти коэффициенты ошибок ниже, чем вычисленные в каналах с замираниями, следовательно, они являются хорошим теоретическим эталоном для сравнения.
Приложения
Благодаря простоте PSK, особенно по сравнению с его конкурентом квадратурной амплитудной модуляцией, он широко используется в существующих технологиях.
Стандарт беспроводной локальной сети, IEEE 802.11b-1999, использует различные PSK в зависимости от требуемой скорости передачи данных. При базовой скорости 1 Мбит / с он использует DBPSK (дифференциальный BPSK). Для обеспечения расширенной скорости 2 Мбит / с используется DQPSK. При достижении 5,5 Мбит / с и полной скорости 11 Мбит / с используется QPSK, но он должен сочетаться с вводом дополнительного кода. Стандарт высокоскоростной беспроводной локальной сети, IEEE 802.11g-2003, имеет восемь скоростей передачи данных: 6, 9, 12, 18, 24, 36, 48 и 54 Мбит / с. В режимах 6 и 9 Мбит / с используется модуляция OFDM, где каждая поднесущая модулируется BPSK. В режимах 12 и 18 Мбит / с используется OFDM с QPSK. Четыре самых быстрых режима используют OFDM с формами квадратурной амплитудной модуляции.
Из-за своей простоты BPSK подходит для недорогих пассивных передатчиков и используется в стандартах RFID, таких как ISO / IEC 14443, который был принят для биометрических паспортов, кредитных карт, таких как American Express, ExpressPay, и многих других приложений.
Bluetooth 2 использует π / 4 { displaystyle pi / 4}
И QPSK, и 8PSK широко используются в спутниковом вещании. QPSK по-прежнему широко используется при потоковой передаче спутниковых каналов SD и некоторых каналов HD. Программы высокого разрешения передаются почти исключительно в 8PSK из-за более высоких битрейтов HD-видео и высокой стоимости спутниковой полосы пропускания. Стандарт DVB-S2 требует поддержки как QPSK, так и 8PSK. Наборы микросхем, используемые в новых спутниковых приставках, таких как серия 7000 компании Broadcom, поддерживают 8PSK и обратно совместимы со старым стандартом.
Исторически сложилось так, что модемы с синхронизацией голосового диапазона , например, Bell 201, 208 и 209 и CCITT V.26, V.27, V.29, V.32 и V.34 использовали PSK.
Двоичная фазовая манипуляция (BPSK)

BPSK (также иногда называемый PRK, фазовой манипуляцией или 2PSK) — это простейшая форма фазовой манипуляции (PSK). В нем используются две фазы, разделенные на 180 °, поэтому их также можно назвать 2-PSK. Не имеет особого значения, где именно расположены точки созвездия, и на этом рисунке они показаны на действительной оси в точках 0 ° и 180 °. Следовательно, он обрабатывает самый высокий уровень шума или искажения до того, как демодулятор примет неверное решение. Это делает его самым надежным из всех PSK. Однако он может модулировать только со скоростью 1 бит / символ (как показано на рисунке) и поэтому не подходит для приложений с высокой скоростью передачи данных.
При наличии произвольного фазового сдвига, вносимого каналом связи, демодулятор (см., Например, цикл Костаса ) не может определить, какая точка совокупности который. В результате данные часто дифференциально кодируются перед модуляцией.
BPSK функционально эквивалентен модуляции 2-QAM.
Реализация
Общая форма для BPSK следует уравнению:
- sn (t) = 2 E b T b cos (2 π ft + π (1 — n)), п = 0, 1. { displaystyle s_ {n} (t) = { sqrt { frac {2E_ {b}} {T_ {b}}}} cos (2 pi ft + pi (1-n)), quad n = 0,1.}
Это дает две фазы, 0 и π. В особой форме двоичные данные часто передаются с помощью следующих сигналов:
- s 0 (t) = 2 E b T b cos (2 π ft + π) = — 2 E b T b cos (2 π фут) { displaystyle s_ {0} (t) = { sqrt { frac {2E_ {b}} {T_ {b}}}} cos (2 pi ft + pi) = — { sqrt { frac {2E_ {b}} {T_ {b}}}} cos (2 pi ft)}
для двоичного «0»
- s 1 (t) = 2 E b T b cos (2 π фут) { displaystyle s_ {1} (t) = { sqrt { frac {2E_ {b}} {T_ {b}}}} cos (2 pi ft)}
для двоичной «1»
, где f — частота основной полосы частот.
Следовательно, пространство сигналов может быть представлено единственной базисной функцией
- ϕ (t) = 2 T b cos (2 π ft) { displaystyle phi (t) = { sqrt { frac {2} {T_ {b}}}} cos (2 pi ft)}
где 1 представлено как E b ϕ (t) { displaystyle { sqrt {E_ {b}}} phi (t)}

Это использование этой базовой функции показано в конце следующего раздела на временной диаграмме сигнала. Самый верхний сигнал — это косинусоидальная волна, модулированная BPSK, которую будет производить модулятор BPSK. Битовый поток, который вызывает этот вывод, показан над сигналом (другие части этого рисунка относятся только к QPSK). После модуляции сигнал основной полосы будет перемещен в полосу высоких частот путем умножения cos (2 π fct) { displaystyle cos (2 pi f_ {c} t)}
Коэффициент битовых ошибок
коэффициент битовых ошибок (BER) BPSK при аддитивном белом гауссовском шуме (AWGN) можно рассчитать как:
- P b = Q (2 E b N 0) { displaystyle P_ {b} = Q left ({ sqrt { frac {2E_ {b}} {N_ {0}}}} right)}
или P е = 1 2 erfc (E b N 0) { displaystyle P_ {e} = { frac {1} {2}} operatorname {erfc} left ({ sqrt { frac {E_ {b}}) {N_ {0}}}} right)}
Поскольку на каждый символ приходится только один бит, это также частота ошибок символа.
Квадратурная фазовая манипуляция (QPSK)

Иногда это называется четырехфазным PSK, 4-PSK или 4- QAM. (Хотя основные концепции QPSK и 4-QAM различны, результирующие модулированные радиоволны точно такие же.) QPSK использует четыре точки на диаграмме созвездия, равномерно распределенные по кругу. С четырьмя фазами QPSK может кодировать два бита на символ, показанные на диаграмме с кодированием Грея, чтобы минимизировать коэффициент ошибок по битам (BER) — иногда ошибочно воспринимается как удвоенный BER, чем BPSK.
Математический анализ показывает, что QPSK может использоваться либо для удвоения скорости передачи данных по сравнению с системой BPSK при сохранении той же полосы пропускания сигнала, либо для поддержания скорости передачи данных BPSK. но необходимо сократить вдвое полосу пропускания. В последнем случае BER QPSK в точности совпадает с BER BPSK — и полагать иначе — это обычная путаница при рассмотрении или описании QPSK. Переданная несущая может претерпевать ряд фазовых изменений.
Учитывая, что каналы радиосвязи распределяются такими агентствами, как Федеральная комиссия по связи, что дает предписанную (максимальную) полосу пропускания, преимущество QPSK над BPSK становится очевидным: QPSK передает в два раза большую скорость передачи данных в заданной полосе пропускания по сравнению с BPSK — при том же BER. Плата за техническое обслуживание состоит в том, что передатчики и приемники QPSK сложнее, чем передатчики для BPSK. Однако с современной технологией электроники снижение стоимости очень умеренное.
Как и в случае с BPSK, на принимающей стороне возникают проблемы с фазовой неоднозначностью, и на практике часто используется дифференциально кодированный QPSK.
Реализация
Реализация QPSK является более общей, чем реализация BPSK, а также указывает на реализацию PSK более высокого порядка. Записывая символы на диаграмме созвездия в виде синусоидальных и косинусоидальных волн, используемых для их передачи:
- sn (t) = 2 E s T s cos (2 π fct + (2 n — 1) π 4), n = 1, 2, 3, 4. { displaystyle s_ {n} (t) = { sqrt { frac {2E_ {s}} {T_ {s}}}} cos left (2 pi f_ {c} t + (2n-1) { frac { pi} {4}} right), quad n = 1,2,3,4.}
Это дает четыре фазы π / 4, 3π / 4, 5π / 4 и 7π / 4 по мере необходимости.
Это приводит к двумерному сигнальному пространству с единицами базисных функций
- ϕ 1 (t) = 2 T s cos (2 π fct) ϕ 2 (t) = 2 T s грех (2 π fct) { displaystyle { begin {align} phi _ {1} (t) = { sqrt { frac {2} {T_ {s}}}} cos left (2 pi f_ {c} t right) \ phi _ {2} (t) = { sqrt { frac {2} {T_ {s}}}} sin left (2 pi f_ { c} t right) end {align}}}
Первая базовая функция используется как синфазная составляющая сигнала, а вторая как квадратурная составляющая сигнала.
Следовательно, совокупность сигналов состоит из 4 точек
- пространства сигнала (± E s 2 ± E s 2). { displaystyle { begin {pmatrix} pm { sqrt { frac {E_ {s}} {2}}} pm { sqrt { frac {E_ {s}} {2}}} end {pmatrix}}.}
Коэффициент 1/2 показывает, что общая мощность поровну делится между двумя несущими.
Сравнение этих базовых функций с функциями для BPSK ясно показывает, как QPSK можно рассматривать как два независимых сигнала BPSK. Обратите внимание, что точки пространства сигнала для BPSK не нуждаются в разделении энергии символа (бита) по двум несущим в схеме, показанной на диаграмме созвездия BPSK.
Системы QPSK могут быть реализованы несколькими способами. Ниже показаны основные компоненты конструкции передатчика и приемника.


Вероятность ошибки
Хотя QPSK можно рассматривать как четвертичную модуляцию, его легче рассматривать как две независимо модулированные квадратурные носители. При такой интерпретации четные (или нечетные) биты используются для модуляции синфазной составляющей несущей, в то время как нечетные (или четные) биты используются для модуляции квадратурной составляющей несущей. BPSK используется на обеих несущих, и их можно независимо демодулировать.
В результате вероятность битовой ошибки для QPSK такая же, как для BPSK:
- P b = Q (2 E b N 0) { displaystyle P_ {b} = Q left ({ sqrt { frac {2E_ {b}} {N_ {0}}}} right)}
Однако для достижения той же вероятности битовой ошибки, что и BPSK, QPSK использует вдвое большую мощность (поскольку два бита передаются одновременно).
Коэффициент ошибок символа определяется следующим образом:
- P s = 1 — (1 — P b) 2 = 2 Q (E s N 0) — [Q (E s N 0)] 2. { displaystyle { begin {align} P_ {s} = 1- left (1-P_ {b} right) ^ {2} \ = 2Q left ({ sqrt { frac {E_ { s}} {N_ {0}}}} right) — left [Q left ({ sqrt { frac {E_ {s}} {N_ {0}}}} right) right] ^ { 2}. End {align}}}
Если отношение сигнал / шум высокое (что необходимо для практических систем QPSK), вероятность ошибки символа может быть приблизительно равна:
- P s ≈ 2 Q (E s N 0) = erfc (E s 2 N 0) = erfc (E b N 0) { displaystyle P_ {s} приблизительно 2Q left ({ sqrt { frac { E_ {s}} {N_ {0}}}} right) = operatorname {erfc} left ({ sqrt { frac {E_ {s}} {2N_ {0}}}} right) = operatorname {erfc} left ({ sqrt { frac {E_ {b}} {N_ {0}}}} right)}
Модулированный сигнал показан ниже для короткого сегмента случайных двоичных данных — поток. Две несущие волны представляют собой косинусоидальную и синусоидальную волну, как показывает анализ пространства сигналов выше. Здесь биты с нечетными номерами назначены синфазному компоненту, а биты с четными номерами — квадратурному компоненту (принимая первый бит за номер 1). Общий сигнал — сумма двух компонентов — показан внизу. Скачки по фазе можно увидеть, поскольку PSK изменяет фазу на каждом компоненте в начале каждого битового периода. Самая верхняя форма волны соответствует описанию, данному для BPSK выше.
.
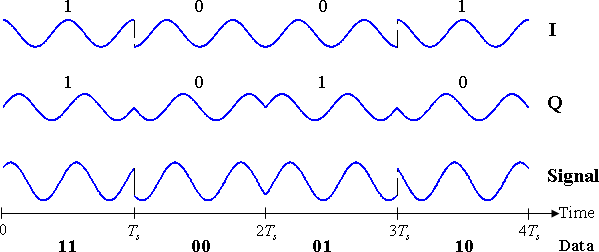
Двоичные данные, которые передаются этим сигналом: 11000110.
- Нечетные биты, выделенные здесь, вносят вклад в синфазную составляющую: 11000110
- Четные биты, выделенные здесь, вносят вклад в квадратурно-фазовую составляющую: 11000110
Варианты
QPSK смещения (OQPSK)
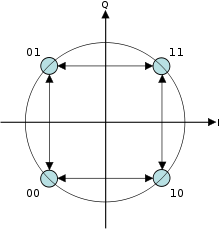
Квадратурная фазовая манипуляция со смещением (OQPSK) — это вариант модуляции с фазовой манипуляцией, использующий четыре различных значения фазы для передачи. Иногда это называют ступенчатой квадратурной фазовой манипуляцией (SQPSK).

Одновременное использование четырех значений фазы (два бита ) для построения символа QPSK может позволить фазе сигнала прыгнуть на столько же как 180 ° за раз. Когда сигнал фильтруется нижними частотами (как это обычно бывает в передатчике), эти фазовые сдвиги приводят к большим колебаниям амплитуды, что является нежелательным качеством в системах связи. При смещении синхронизации нечетных и четных битов на один битовый период или половину периода символа синфазная и квадратурная составляющие никогда не изменятся одновременно. На диаграмме созвездия, показанной справа, можно увидеть, что это ограничит фазовый сдвиг не более чем на 90 ° за раз. Это дает гораздо меньшие колебания амплитуды, чем QPSK без смещения, и иногда это предпочтительнее на практике.
На рисунке справа показана разница в поведении фазы между обычным QPSK и OQPSK. Видно, что на первом графике фаза может измениться сразу на 180 °, а в OQPSK изменения никогда не превышают 90 °.
Модулированный сигнал показан ниже для короткого сегмента случайного потока двоичных данных. Обратите внимание на сдвиг на половину периода символа между двумя составляющими волнами. Внезапные сдвиги фазы происходят примерно в два раза чаще, чем при QPSK (поскольку сигналы больше не изменяются вместе), но они менее серьезны. Другими словами, величина скачков меньше в OQPSK по сравнению с QPSK.

SOQPSK
Безлицензионный сформированный -смещение QPSK (SOQPSK) совместим с Feher- запатентованный QPSK (FQPSK ) в том смысле, что детектор QPSK с интегрированием и сбросом смещения дает одинаковый выходной сигнал независимо от типа используемого передатчика.
Эти модуляции тщательно формируют I и формы волны Q, так что они изменяются очень плавно, и сигнал остается постоянной амплитуды даже во время переходов сигнала. (Вместо мгновенного перехода от одного символа к другому или даже линейного, он плавно перемещается по кругу с постоянной амплитудой от одного символа к другому.) Модуляция SOQPSK может быть представлена как гибрид QPSK и MSK : SOQPSK имеет ту же совокупность сигналов, что и QPSK, однако фаза SOQPSK всегда стационарна.
Стандартное описание SOQPSK-TG включает троичные символы. SOQPSK — одна из наиболее распространенных схем модуляции в применении к спутниковой связи LEO.
π / 4-QPSK

В этом варианте QPSK используются два идентичных созвездия, повернутых на 45 ° (π / 4 { displaystyle pi / 4}

Одно свойство, которым обладает эта схема модуляции, заключается в том, что если модулированный сигнал представлен в комплексной области, переходы между символами никогда не проходят через 0. Другими словами, сигнал не проходит через начало координат. Это снижает динамический диапазон колебаний сигнала, что желательно при разработке сигналов связи.
С другой стороны, π / 4 { displaystyle pi / 4}
Модулированный сигнал показан ниже для короткого сегмента случайного потока двоичных данных. Конструкция такая же, как и для обычного QPSK. Последовательные символы взяты из двух созвездий, показанных на схеме. Таким образом, первый символ (11) взят из «синего» созвездия, а второй символ (0 0) взят из «зеленого» созвездия. Обратите внимание, что величины двух составляющих волн изменяются при переключении между созвездиями, но общая величина сигнала остается постоянной (постоянная огибающая ). Фазовые сдвиги находятся между двумя предыдущими временными диаграммами.

DPQPSK
Квадратурная фазовая манипуляция с двойной поляризацией (DPQPSK) или QPSK с двойной поляризацией — включает поляризационное мультиплексирование двух разных сигналов QPSK, таким образом улучшая спектральную эффективность в 2 раза. Это экономичная альтернатива использованию 16-PSK вместо QPSK для удвоения спектральной эффективности.
PSK высшего порядка
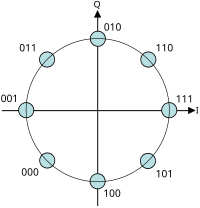
Для построения совокупности PSK можно использовать любое количество фаз, но 8-PSK обычно является развернутой совокупностью PSK высшего порядка. При более чем 8 фазах частота ошибок становится слишком высокой, и доступны более качественные, хотя и более сложные модуляции, такие как квадратурная амплитудная модуляция (QAM). Хотя может использоваться любое количество фаз, тот факт, что совокупность обычно должна иметь дело с двоичными данными, означает, что количество символов обычно является степенью 2, чтобы обеспечить целое число битов на символ.
Коэффициент битовых ошибок
Для общего M-PSK не существует простого выражения для вероятности ошибки символа, если M>4 { displaystyle M>4}
- P s = 1 — ∫ — π / M π / M p θ r (θ r) d θ r, { displaystyle P_ {s} = 1- int _ {- pi / M } ^ { pi / M} p _ { theta _ {r}} left ( theta _ {r} right) d theta _ {r},}
где
- p θ r (θ r) = 1 2 π e — 2 γ s sin 2 θ r ∫ 0 ∞ V e — 1 2 (V — 2 γ s cos θ r) 2 d V, V = r 1 2 + r 2 2, θ р знак равно загар — 1 (р 2 р 1), γ s знак равно Е s N 0 { Displaystyle { begin {align} p _ { theta _ {r}} left ( theta _ {r} right) = { frac {1} {2 pi}} e ^ {- 2 gamma _ {s} sin ^ {2} theta _ {r}} int _ {0} ^ { infty} Ve ^ {- { frac {1} {2}} left (V-2 { sqrt { gamma _ {s}}} cos theta _ {r} right) ^ {2}} , dV, \ V = { sqrt {r_ {1} ^ {2} + r_ {2} ^ {2}}}, \ theta _ {r} = tan ^ {- 1} left ({ frac {r_ {2}} {r_ {1}}} r ight), \ gamma _ {s} = { frac {E_ {s}} {N_ {0}}} end {align}}}
и r 1 ∼ N (E s, 1 2 N 0) { displaystyle r_ {1} sim N left ({ sqrt {E_ {s}}}, { frac {1} {2}} N_ {0} right)}


Это может быть приблизительно для высокого M { displaystyle M}

- P s ≈ 2 Q (2 γ s sin π M). { displaystyle P_ {s} приблизительно 2Q left ({ sqrt {2 gamma _ {s}}} sin { frac { pi} {M}} right).}
Бит- вероятность ошибки для M { displaystyle M}
- P b ≈ 1 k P s. { displaystyle P_ {b} приблизительно { frac {1} {k}} P_ {s}.}
(Использование кодирования Грея позволяет нам приблизить расстояние Ли ошибок как Расстояние Хэмминга ошибок в декодированном потоке битов, которое легче реализовать аппаратно.)
На графике слева сравниваются коэффициенты битовых ошибок BPSK, QPSK (которые являются то же, что и отмечалось выше), 8-PSK и 16-PSK. Видно, что модуляция более высокого порядка демонстрирует более высокие коэффициенты ошибок; однако взамен они обеспечивают более высокую скорость необработанных данных.
Границы частоты ошибок для различных схем цифровой модуляции могут быть вычислены с применением объединения к сигнальной совокупности.
Спектральная эффективность
Ширина полосы (или спектральная) эффективность схем модуляции M-PSK увеличивается с увеличением порядка модуляции M (в отличие, например, от M-FSK ):
- ρ = журнал 2 M 2 [бит / с ⋅ Гц] { displaystyle rho = { frac { log _ {2} M} {2}} quad [{ text {bits}} / { text {s }} cdot { text {Hz}}]}
То же соотношение сохраняется и для M-QAM.
Дифференциальная фазовая манипуляция (DPSK)
Дифференциальное кодирование
Дифференциальная фазовая манипуляция (DPSK) — это распространенная форма фазовой модуляции, которая передает данные путем изменения фазы несущей волны. Как упоминалось для BPSK и QPSK, существует неоднозначность фазы, если совокупность поворачивается некоторым эффектом в канал связи, через который проходит сигнал. Эту проблему можно решить, используя данные для изменения, а не для установки фазы.
Например, в дифференциально-кодированной BPSK двоичной «1» может быть передан путем добавления 180 ° к текущей фазе и двоичного «0» путем добавления 0 ° к текущей фазе. Другой вариант DPSK — это симметричная дифференциальная фазовая манипуляция, SDPSK, где кодирование будет составлять + 90 ° для «1» и -90 ° для «0».
В дифференциально кодированной QPSK (DQPSK) фазовые сдвиги составляют 0 °, 90 °, 180 °, -90 °, что соответствует данным «00», «01», «11», «10». Этот вид кодирования может быть демодулирован таким же образом, как и для недифференциальной PSK, но фазовые неоднозначности можно игнорировать. Таким образом, каждый принятый символ демодулируется в одну из точек M { displaystyle M}
Модулированный сигнал показан ниже как для DBPSK, так и для DQPSK, как описано выше. На рисунке предполагается, что сигнал начинается с нулевой фазы, и поэтому в обоих сигналах есть фазовый сдвиг в t = 0 { displaystyle t = 0}

Анализ показывает, что дифференциальное кодирование примерно вдвое увеличивает количество ошибок по сравнению с обычным M { displaystyle M}

Одно из самых популярных приложений DPSK — это стандарт Bluetooth, где π / 4 { displaystyle pi / 4}
Демодуляция

Для сигнала, который был закодирован дифференциально, существует очевидный альтернативный метод демодуляции. Вместо обычной демодуляции и игнорирования неоднозначности фазы несущей сравнивается фаза между двумя последовательными принятыми символами и используется для определения того, какими должны были быть данные. Когда дифференциальное кодирование используется таким образом, схема известна как дифференциальная фазовая манипуляция (DPSK). Обратите внимание, что это немного отличается от просто дифференциально кодированной PSK, поскольку при приеме принятые символы не декодируются один за другим в точки совокупности, а вместо этого напрямую сравниваются друг с другом.
Вызвать полученный символ в k { displaystyle k}



- r k = E s e j ϕ k + n k. { displaystyle r_ {k} = { sqrt {E_ {s}}} e ^ {j phi _ {k}} + n_ {k}.}
Переменная решения для k — 1 { displaystyle k-1}





- rkrk — 1 ∗ = E sej (φ k — φ k — 1) + E sej φ knk — 1 ∗ + E se — j φ k — 1 nk + nknk — 1 * { displaystyle r_ {k} r_ {k-1} ^ {*} = E_ {s} e ^ {j left ( varphi _ {k} — varphi _ {k-1} right) } + { sqrt {E_ {s}}} e ^ {j varphi _ {k}} n_ {k-1} ^ {*} + { sqrt {E_ {s}}} e ^ {- j varphi _ {k-1}} n_ {k} + n_ {k} n_ {k-1} ^ {*}}
где верхний индекс * обозначает комплексное сопряжение. В отсутствие шума фаза этого сигнала равна ϕ k — ϕ k — 1 { displaystyle phi _ {k} — phi _ {k-1}}
Вероятность ошибки для DPSK в целом трудно вычислить, но в случае DBPSK это:
- P b = 1 2 e — E b N 0, { displaystyle P_ {b } = { frac {1} {2}} e ^ {- { frac {E_ {b}} {N_ {0}}}},}
который при численной оценке лишь немного хуже обычного BPSK, особенно при более высоких значениях E b / N 0 { displaystyle E_ {b} / N_ {0}}
Использование DPSK устраняет необходимость в возможных сложных схемах восстановления несущей для обеспечения точной оценки фазы и может быть привлекательной альтернативой обычному PSK.
В оптической связи данные могут быть модулированы по фазе лазера дифференциальным способом. Модуляция представляет собой лазер, который излучает непрерывную волну, и модулятор Маха – Цендера, который принимает электрические двоичные данные. В случае BPSK лазер передает поле без изменений для двоичной «1» и с обратной полярностью для «0». Демодулятор состоит из интерферометра линии задержки, который задерживает один бит, поэтому два бита можно сравнивать за один раз. При дальнейшей обработке используется фотодиод для преобразования оптического поля в электрический ток, так что информация возвращается в исходное состояние.
Коэффициенты ошибок по битам DBPSK и DQPSK сравниваются с их недифференциальными аналогами на графике справа. Потери при использовании DBPSK достаточно малы по сравнению с уменьшением сложности, которое часто используется в системах связи, которые иначе использовали бы BPSK. Однако для DQPSK потеря производительности по сравнению с обычным QPSK больше, и разработчик системы должен сбалансировать это с уменьшением сложности.
Пример: BPSK с дифференциальным кодированием
Схема системы дифференциального кодирования / декодирования
В k th { displaystyle k ^ { textrm {th}}}



- ek = ek — 1 ⊕ bk { displaystyle , e_ {k} = e_ {k-1} oplus b_ {k}}
где ⊕ { displaystyle oplus {}}

Итак, ek { displaystyle e_ {k}}

Полученный сигнал демодулируется для получения ek = ± 1 { displaystyle e_ {k} = pm 1}
- bk = ek ⊕ ek — 1, { displaystyle b_ {k} = e_ {k} oplus e_ {k-1},}
поскольку двоичное вычитание аналогично двоичному сложению.
Следовательно, bk = 1 { displaystyle b_ {k} = 1}






Дифференциальные схемы для других модуляций PSK могут быть разработаны аналогичным образом. Формы сигналов для DPSK такие же, как для PSK с дифференциальным кодированием, приведенные выше, поскольку единственное изменение между двумя схемами — на приемнике.
Кривая BER для этого примера сравнивается с обычным BPSK справа. Как упоминалось выше, хотя частота ошибок увеличивается примерно вдвое, увеличение E b / N 0 { displaystyle E_ {b} / N_ {0}}

Взаимная информация с аддитивным белым гауссовским шумом

взаимная информация PSK может быть оценена в аддитивном гауссовском шуме посредством численного интегрирования его определения. Кривые взаимной информации насыщаются до количества битов, переносимых каждым символом в пределе бесконечного отношения сигнал / шум E s / N 0 { displaystyle E_ {s} / N_ {0}}
При промежуточных значениях отношения сигнал / шум взаимная информация (MI) хорошо аппроксимируется следующим образом:
- MI ≃ log 2 (4 π e E s N 0). { displaystyle { textrm {MI}} simeq log _ {2} left ({ sqrt {{ frac {4 pi} {e}} { frac {E_ {s}} {N_ {0) }}}}} right).}
Взаимная информация PSK по каналу AWGN обычно находится дальше от пропускной способности канала AWGN, чем форматы модуляции QAM.
См. Также
| Викискладе есть носители, относящиеся к Квантованной фазовой модуляции. |
Примечания
Ссылки
Обозначения и теоретические результаты в этой статье основаны на материалах, представленных в следующих источниках:
- Proakis, John G. (1995). Цифровая связь. Сингапур: Макгроу Хилл. ISBN 0-07-113814-5.
- Диван, Леон В. II (1997). Цифровая и аналоговая связь. Река Аппер Сэдл, Нью-Джерси: Прентис-Холл. ISBN 0-13-081223-4.
- Хайкин, Саймон (1988). Цифровые коммуникации. Торонто, Канада: John Wiley Sons. ISBN 0-471-62947-2.



 .
.





















 .
.
 для двоичного «0»
для двоичного «0» для двоичной «1»
для двоичной «1»
 или P е = 1 2 erfc (E b N 0) { displaystyle P_ {e} = { frac {1} {2}} operatorname {erfc} left ({ sqrt { frac {E_ {b}}) {N_ {0}}}} right)}
или P е = 1 2 erfc (E b N 0) { displaystyle P_ {e} = { frac {1} {2}} operatorname {erfc} left ({ sqrt { frac {E_ {b}}) {N_ {0}}}} right)}



![{ displaysty le { begin {align} P_ {s} = 1- left (1-P_ {b} right) ^ {2} \ = 2Q left ({ sqrt { frac {E_ {s}) } {N_ {0}}}} right) - left [Q left ({ sqrt { frac {E_ {s}} {N_ {0}}}} right) right] ^ {2}. end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f83586ff4bc11f3ac6369902becbeba4313b675a)





![{ displaystyle rho = { frac { log _ {2} M} {2}} quad [{ text {bits}} / { text {s}} cdot { текст {Гц}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0750a97fea3020cd5bc401183d6ceb8b35dc51a3)





