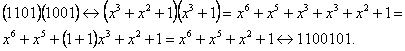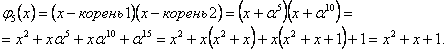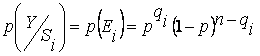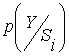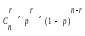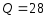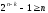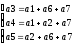Вес вектора ошибки

Если комбинации кода известны и
он используется для исправления ошибок, то способ разбиения множества U на подмножества Ai
определяется статистикой ошибок, возникающих в его комбинациях. Обычно это
разбиение выполняется так, чтобы минимизировать среднюю вероятность появления
ложной комбинации на входе декодера.

В дальнейшем будем рассматривать
только двоичные коды, как получившие наибольшее распространение.

20. Понятие «вектор ошибок»

Для удобства представления
ошибок, возникающих в комбинациях двоичного корректирующего кода, используется
понятие вектор ошибок. Под вектором ошибок понимается комбинация длины N символов с 2-мя возможными значениями 0 и 1, в которой
единицы занимают позиции в комбинациях кода, на которых стоят ошибочные символы.
Все остальные позиции заняты нулями. Вес вектора ошибок ei W(ei)
= ν, где ν – кратность ошибок.

Искаженная комбинация кода V*  при использовании понятия вектор ошибок
может быть представлена как результат суммы по модулю два одноименных символов
неискаженной комбинации V и вектора ошибок ei , то есть

    (7)

Поскольку в комбинации кода может
быть искажено любое число символов в пределах n и эти
символы могут занимать любые позиции в комбинации, то число ненулевых векторов
ошибок:

      (8)

где единица соответствует
нулевому вектору ошибок.

Если известен вектор ошибок, то
процедура исправления ошибок в принятой комбинации состоит в сложении по модулю
два принятой комбинации с вектором ошибок.

Действительно,

21. Методы определения разрядности блокового корректирующего
кода и нахождение его комбинаций.

Говоря ранее о разбиении
множества запрещенных комбинаций U на подмножества   Ai, мы предполагали, что комбинации кода известны,
однако практике это не так.

Известно число комбинаций,
которые должны входить в код, и подлежащие исправлению ошибки в этих
комбинациях исходя из статистики появления ошибок. При этом задача заключается
в том, чтобы найти код, который бы содержал n комбинаций и позволял исправлять известные ошибки.

Источник

Определение
вектора

Вектором
называется упорядоченное множество
из 
 элементов
поля, обозначаемое как 
.
Величины 
 называются
компонентами (координатами) вектора.
Число компонентов вектора 
 называется
длиной вектора. Векторы считаются
равными, если равны их соответствующие
компоненты. Число ненулевых компонентов
вектора называют весом вектора [33].

Сложение
двух векторов длины 
 определяется
следующим образом:


.

Умножение
элемента поля на вектор производится
покомпонентно:


,

причем
сложение и умножение компонентов
векторов происходит по правилам сложения
и умножения в поле 
.

Для
векторов введено понятие нормы [25, 33],
которая для вектора 
 определяется
как 
,
где символ 
 означает
суммирование в поле действительных
чисел. Если компоненты вектора принадлежат
двоичному полю, то норма вектора совпадает
с числом его ненулевых компонентов,
т.е. с его весом.

Вектор 
,
где 
 –
элементы поля, называют линейной
комбинацией векторов 
.
Векторы 
 называются
линейно зависимыми, если в 
 существуют
такие элементы 
,
по крайней мере один из которых не равен
нулю, такие что 
 и
линейно независимыми в противном случае.
Если векторы линейно зависимы, то любой
из них может быть выражен через линейную
комбинацию остальных.

Определение
векторного пространства

Множество 
 называется
векторным пространством, если для него
выполняются следующие аксиомы:

V.
1. Множество 
 является
аддитивной абелевой группой.

V.2.
Для любого вектора 
 и
любого скаляра – элемента 
 поля 
 определено
произведение 
,
являющееся вектором. Это произведение
определено так, что 
,
где 
 –
единичный элемент поля 
.

V.3.
Выполняются законы дистрибутивности


 и 
,

где    
 –
скаляры, а 
 и 
 –
векторы.

V.4.
Выполняется закон ассоциативности


,

где    
 –
скаляры, а 
 –
вектор.

Свойства
векторного пространства

1.
Максимальное число линейно независимых
векторов в 
 называется
размерностью пространства 
 над
полем 
.

2.
Совокупность 
 любых
линейно независимых векторов называется
базисом и-мерного пространства, если
каждый из векторов пространства может
быть представлен в виде линейной
комбинации этих векторов. Векторы
совокупности называются базисными.

3.
Подмножество 
 векторного
пространства 
 такое,
что любая линейная комбинация векторов
этого подмножества снова принадлежит 
,
называется подпространством пространства 
.
Легко проверить, что все векторы
подпространства удовлетворяют аксиомам
V.1 – V.4. Очевидно, что размерность
подпространства не превышает размерности
пространства, т.к. во всем пространстве
содержится не более 
 линейно
независимых векторов. Каждое подпространство
можно рассматривать как самостоятельное
пространство. Следовательно, каждое
подпространство имеет свой базис.

4.
Скалярным произведением двух векторов
одинаковой длины 
: 
 и 
 называется
скаляр, определяемый как


.

Можно
показать, что 
 и 
.

Если
скалярное произведение двух векторов
равно нулю, то говорят, что эти векторы
ортогональны. Два пространства называются
взаимно ортогональными, если каждый
вектор одного пространства ортогонален
любому вектору другого пространства.

Множество
всех векторов пространства 
,
ортогональных подпространству 
,
образуют подпространство 
 пространства 
.
Подпространство 
 часто
называют нулевым пространством для 
.

Можно
показать, что если 
 –
подпространство размерности 
 
-мерного
векторного пространства 
,
то размерность нулевого пространства
равна 
.

5.
Для векторного пространства определено
понятие расстояния между двумя векторами,
которое совпадает с нормой разности
этих векторов


,

где
суммирование производится в поле
действительных чисел.

5.3.5.
Конечные поля

Определение
конечного поля

Ранее
в 1.3.2 дано определение поля 
 как
коммутативного кольца с единицей, в
котором каждый ненулевой элемент имеет
мультипликативный обратный элемент. В
теории помехоустойчивых кодов весьма
важное значение имеют поля, образованные
конечным множеством элементов – так
называемые конечные поля Галуа (Galois
Field), обозначаемые 
.
В связи с этим дадим их развернутое
определение.

Конечным
полем 
 называется
конечное множество элементов, замкнутое
по отношению к двум заданным в нем
операциям комбинирования элементов.
Под замкнутостью понимается тот факт,
что результаты операций не выходят за
пределы конечного множества введенных
элементов. Для конечных полей выполняются
следующие аксиомы.

  1. GF.1.
    Из введенных операций над элементами
    поля одна называется сложением и
    обозначается как 
    ,
    а другая — умножением и обозначается
    как 
    .

  2. GF.2.
    Для любого элемента 
     существует
    обратный элемент по сложению 
     и
    обратный элемент по умножению 
     (если 
    )
    такие, что 
     и 
    .
    Наличие обратных элементов позволяет
    наряду с операциями сложения и умножения
    выполнять также вычитание и деление: 
    , 
    .
    Поэтому иногда просто говорят, что в
    поле определены все четыре арифметические
    операции (кроме деления на 0).

  3. GF.3.
    Поле всегда содержит мультипликативную
    единицу 1 и аддитивную единицу 0, такие
    что 
    ,
    и 
     для
    любого элемента поля.

  4. GF.4.
    Для введенных операций выполняются
    обычные правила ассоциативности 
    , 
    ,
    коммутативности 
    , 
     и
    дистрибутивности 
    .

  5. GF.5.
    Результатом сложения или умножения
    двух элементов поля является третий
    элемент из того же конечного множества.

Аксиомы
GF.1 – GF.5 являются общими для полей как
с конечным, так и с бесконечным числом
элементов. Специфику же конечного поля
определяет аксиома GF.5, где ключевыми
являются слова «из того же конечного
множества».

Требование
конечности множества определяет ряд
ограничений как на количество элементов
поля 
,
так и на понятия «сложение» и «умножение».

Конечные
поля существуют не при любом числе
элементов, а только в том случае, если
их количество – простое число 
 или
его степень 
,
где 
 –
целое. В первом случае поле 
 называется
простым, а во втором – расширением 
 простого
поля.

Очевидно,
операции комбинирования элементов
конечного поля не могут быть обычными
сложением и умножением. Выполнение
аксиомы GF.5 для простого конечного поля
обеспечивается совершением арифметических
операций по модулю числа 
,
которое носит название характеристики
конечного поля. Можно убедиться, что в
кольце вычетов по модулю 
 (см. 5.3.1)
каждый ненулевой элемент имеет обратный
элемент тогда и только тогда, когда 
 –
простое число [25, 26, 33]. Следовательно,
кольцо вычетов по модулю простого
числа 
 является
простым полем 
.
Элементами этого поля являются целые
числа 
.
Операции сложения и умножения в таком
поле производятся по модулю 
.
Пример простейшего двоичного
поля 
 приведен
в 5.3.3.

Элементами 
 расширенного
поля 
 могут
быть, например, все многочлены степени 
 или
меньше, коэффициенты которых лежат в
простом поле 
.
Число 
 называется
порядком расширенного поля и определяет
количество различных многочленов.

Правила
сложения и умножения полиномов –
элементов расширенного конечного поля
получаются из обычных правил сложения
и умножения полиномов с последующим
приведением результата по модулю
некоторого специального многочлена 
 степени 
.
Такое приведение эквивалентно делению
многочлена результата на 
 и
использованию только остатка.

Очевидно,
любые результаты вычислений в поле
после приведения по модулю 
 должны
оставаться обратимыми – только в этом
случае наша система образует поле. Для
этого используемый полином 
 должен
быть неприводимым в поле 
,
т.е. его нельзя разложить на множители,
используя только многочлены с
коэффициентами из 
.
Это означает также, что 
 не
имеет корней в поле 
.
Аналогом неприводимого полинома является
простое число в поле вещественных чисел.

К
сожалению, регулярных методов поиска
неприводимых полиномов не существует,
они обычно определяются перебором. К
настоящему времени имеются подробные
таблицы неприводимых полиномов [30, 33].

Особым
свойством конечных полей является связь
между собой всех ненулевых элементов 
 и
возможность выражения каждого из них
через один элемент 
,
называемый примитивным, как некоторую
целую степень этого элемента.
Множество 
 ненулевых
элементов расширения 
 образует
циклическую мультипликативную группу
(см. 5.3.2), т.е. элементы находятся между
собой в соотношении 
.
Примитивных элементов в 
 может
быть несколько.

Построение
конечного поля

Построим
конечное поле 
 и
его расширение 
.
Пусть элементами 
 являются
0 и 1, а элементами 
 –
16 всевозможных полиномов степени 3 и
менее с коэффициентами из 
:


.

Теперь
необходимо определить операции над
элементами таким образом, чтобы их
результаты не давали новых элементов,
кроме уже введенных.

В
поле 
 обычные
операции умножения (на 0 и 1) и деления
(на 1) не выводят результат за пределы
множества 0; 1. Однако при сложении и
вычитании элементов это требование
может уже не выполняться: 
; 
 и
т. д. Свойства конечного поля будут,
очевидно, соблюдаться, если в качестве
операции сложения использовать
суммирование по модулю 2 
:


; 
; 
; 
.

(5.9)

причем
операции сложения и вычитания в
поле 
 совпадают.
Этим мы будем пользоваться в дальнейшем,
заменяя, например, полином вида 
 на 
 в
тех случаях, когда полиномы заданы над
полем характеристики 2. Если, однако,
характеристика поля 
,
такая замена неправомерна, и полиномы
каждого вида нужно рассматривать
самостоятельно.

В
поле 
 операцией,
которая может вывести результат за
пределы поля, является умножение
многочленов. Обычное перемножение может
дать полином степени больше 3, не
принадлежащий множеству элементов 
.
Действительно, используя представление
полиномов через векторы их коэффициентов
[26], а также учитывая (5.9), получим

Поэтому
введем дополнительное условие,
чтобы 
 удовлетворял
некоторому уравнению степени 
,
например, 
 или 
.
Тогда 
; 
; 
 и
т.д., а 
,
т.е. не выходит за пределы поля 
.

Нетрудно
видеть, что результат проделанного
преобразования полинома 
 эквивалентен
вычислению остатка от его деления на
полином 
,
т.е. приведению произведения многочленов
по модулю 
:


 –
частное


 –
остаток.

Или 
.
Делением на полиномы первой степени 
 и 
,
и второй степени 
, 
 и
 можно
убедиться, что рассматриваемый
многочлен 
 неприводим
над 
,
а следовательно, не имеет в нем корней.
В противном случае 
 раскладывался
бы на сомножители 
 и 
,
ибо корнями в поле 
 могут
быть только 0 или 1.

Для
нахождения примитивных элементов поля,
как и неприводимых полиномов, приходится
прибегать к таблицам. В нашем примере
поля 
,
задаваемого многочленом 
,
примитивным элементом является 
.
Последовательно применяя равенства 
 и 
 (или,
что эквивалентно, 
),
получим упорядоченное по степеням
примитивного элемента 
 множество
элементов 
,
составляющее конечное поле 
.

В
табл. 5.2 даны различные представления
элементов 
 поля 
,
заданного полиномом 
,
а также полиномом 
.

Представление
элементов поля по степеням примитивного
элемента 
 удобно,
в частности, при умножении элементов
друг на друга. Для этого достаточно
сложить их степени по модулю 
 (применительно
к табл. 5.2 – по модулю 15). Например,


.

Прямые
вычисления дают то же, но более трудоемко:

Таблица
5.2. Различные представления элементов
поля 

Ненулевые
элементы поля

Представление
элементов поля через

Представление
через

полином

вектор

степень 

вектор

степень 

1

1

Ненулевые
элементы 
 расположены
в порядке нарастания степени примитивного
элемента и образуют циклическую группу
порядка 15. При этом 
, 
, 
,
… , 
 и
т.д.

Нетрудно
убедиться, что примитивным в поле 
 является
не только один элемент 
,
но и 
, 
, 
 и
ряд других (предлагается их отыскать
самостоятельно), а 
 и 
 таковыми
не являются.

Основные
свойства конечных полей и полиномов

Связь
между элементами конечного поля

Все
ненулевые элементы 
 конечного
поля 
 являются
степенями одного примитивного элемента:


,  
;  
.

Порядок
элемента поля

Порядком 
 элемента 
 конечного
поля называется наименьшее значение 
,
для которого 
.
Пусть 
.
Поскольку ненулевые элементы 
 образуют
циклическую группу, порядок элемента 
 может
быть определен из равенства


,

где    
 –
наибольший общий делитель. Порядки
элементов 
 лежат
в пределах от 1 (элемент 
)
до 
 (примитивные
элементы), но 
 всегда
кратно порядку элемента.

Возведение
многочлена над полем 
 в
степень 

Если 
 –
произвольный многочлен, коэффициенты
которого лежат в 
,
то 
.
Справедливость этого утверждения
вытекает из того, что все по парные или
многократные произведения в 
 появляются
с коэффициентами, которые делятся на 
,
и значит, равны 0 в 
.

Так
для многочлена над полем
характеристики 
 справедливо 
,
в чем можно убедиться на примере:


,

Корни
полиномов

Ключевым
при построении кодов и их декодировании
является вопрос о корнях полиномов,
соответствующих кодовым комбинациям.
Напомним, что из теории полиномов над
полем вещественных чисел (не конечных!)
известно, что полином степени 
 всегда
имеет 
 корней,
только не все они обязательно лежат в
поле вещественных чисел (на вещественной
оси). Часть корней может находиться в
поле комплексных чисел как некотором
расширении поля вещественных чисел.

Известная
аналогия этому имеется и в конечных
полях. Любой многочлен степени 
,
в том числе и неприводимый над полем 
 (не
имеющий корней среди элементов этого
поля), всегда имеет 
 корней
в расширении 
,
и этими корнями является часть элементов
поля 
.
Как элементы конечного поля, корни
находятся между собой в определенном
соотношении. Если 
 –
неприводимый полином с коэффициентами
из 
 и 
 –
его корень, то 
 также
являются его корнями. В поле 
 корнями
неприводимого полинома степени 
 будут 
.

Полиномы 

Для
дальнейшего обсуждения процедур
кодирования и декодирования полезно
иметь в виду следующие свойства многочлена
вида 
.
Для любого элемента 
 как
циклической группы справедливо
равенство 
.
Это означает, что любой из элементов 
 является
корнем уравнения 
 или,
что то же самое, корнем полинома 
 или 
.
Нулевой элемент 
 –
корень полинома 
,
а каждый из ненулевых элементов поля 
 –
один из корней полинома 
.
Таким образом,


.

(5.10)

Пусть 
 –
порядок элемента поля 
,
т.е. 
.
Следовательно, 
 –
корень полинома 
.
Если 
 является
также и корнем неприводимого многочлена 
,
то 
 делится
без остатка на 
.

В
более общем случае минимальное значение 
,
для которого произвольный многочлен 
 без
кратных корней делит 
,
совпадает с наименьшим общим кратным
(НОК) порядков корней 
.

Многочлен 
 делится
на 
 только
в том случае, если 
 делится
на 
.
Действительно, если корни 
 являются
также корнями 
,
то 
 должно
делиться на 
.

Циклотомические
классы

Каждый
из корней 
 полинома 
 в
поле 
 есть
степень примитивного элемента 
.
Показатели степеней, соответствующие
корням


, 
, 
, 
,…,

образуют
циклотомический класс чисел 
 по
модулю 
,
а весь набор показателей степеней
примитивного элемента в поле 
 распадается
на не перекрывающиеся циклотомические
классы 
.
Индекс 
 равен
наименьшему из чисел в классе и называется
представителем класса по модулю 
.

С
другой стороны, как отмечалось в 5.3.5,
каждый из 
 ненулевых
элементов 
 поля 
 является
одним из корней полинома 
,
который, в свою очередь, раскладывается
на произведение неприводимых
полиномов
 меньшей
степени. Каждый из циклотомических
классов содержит набор показателей
степеней примитивного элемента,
соответствующих корням одного из
полиномов 
.

Убедимся
в этом на примере полинома 
 над
полем 
.
Поскольку сложение и вычитание по модулю
2 здесь неразличимы, то записи 
 и 
 эквивалентны.
Разложение 
 на
неприводимые полиномы 
 выглядит
следующим образом [30]:


.

В
табл. 5.3 приведено распределение элементов
поля 
,
представленных степенями примитивного
элемента 
,
по циклотомическим классам 
 с
указанием соответствующих им неприводимых
полиномов 
.

Класс 
 содержит
один элемент, 
 –
два элемента, а классы 
, 
 и 
 –
по четыре элемента. Это значит, что
неприводимый над полем 
 полином,
имеющий в качестве корня элемент 
 поля 
,
должен быть полиномом первой степени,
т.е. 
.
Корни 
 и 
 принадлежат
неприводимому полиному 2-й степени,
который определяется по известному
правилу:

Остальные
ненулевые элементы поля 
 являются
корнями неприводимых полиномов 
, 
, 
 четвертой
степени, вычисляемых аналогичным
образом.

Имея
в виду связь между корнями одного
полинома, часто об его корнях говорят
в единственном числе: «неприводимый
полином имеет корень…», понимая под
корнем один элемент поля, соответствующий,
как правило, младшему из чисел
циклотомического ряда, называемому его
представителем.

Таблица
5.3. Распределение элементов поля 
 по
циклотомическим классам

Корни 

Циклотомические
классы 

Полиномы 

Минимальные
многочлены

Рассмотренное
распределение элементов конечного поля
по циклотомическим классам позволяет
лучше понять следующее важное в теории
кодирования понятие. Минимальным
многочленом или минимальной функцией
элемента 
 поля 
 называется
многочлен 
 с
коэффициентами из 
 наименьшей
степени, для которого 
 является
корнем, т.е. 
.
Обсудим его основные свойства.

Прежде
всего, очевидно, что минимальный многочлен
должен быть неприводимым, иначе он
раскладывался бы на полиномы меньшей
степени.

Любой
другой полином, имеющий тот же корень 
,
что и минимальный, делится на 
.
На 
 делится
и полином 
,
т.к. корнями последнего в соответствии
с (5.10) будут все ненулевые элементы
поля 
.
Степень минимального многочлена
определяется количеством компонентов
циклотомического класса, которому
соответствует его корень (табл. 5.3).
Действительно, минимальный многочлен,
показатели корней которого принадлежат
циклотомическому классу 
,
может быть записан в виде


.

(5.11)

Для 
 (см.
5.3.5):


.

Аналогично
для 
:


.

С
учетом (5.10) справедливо равенство


,

где    
 пробегает
все множество классов по модулю 
,
т.е. многочлен 
 раскладывается
на произведение минимальных многочленов
элементов, показатели которых принадлежат
каждому из циклотомических классов по
модулю 
.

Минимальные
многочлены элементов 
 и 
 равны.
В частности, в поле 
 равны
минимальные многочлены элементов 
 и 
.
В этом можно убедиться, обратив внимание
на тот факт, что элементы 
 и 
 всегда
соответствуют одному циклотомическому
классу (табл. 5.3), а следовательно,
принадлежат набору корней одного
неприводимого полинома. Более того,
между собой равны минимальные многочлены
всех элементов, соответствующих одному
циклотомическому классу, т.к. любые два
соседние из таких элементов находятся
в соотношении 
 и 
.

И
еще об одном свойстве минимального
многочлена, имеющем отношение к нахождению
примитивных элементов поля. Минимальный
многочлен, корнем которого является
примитивный элемент поля, называется
примитивным многочленом. Его степень
всегда равна 
.
Для практических приложений важно иметь
в виду следующее. В тех случаях, когда
неприводимый многочлен 
,
задающий операции в поле, является также
и примитивным многочленом, примитивным
элементом поля будет элемент 
.

Таблицы
неприводимых многочленов [33] обычно
содержат сведения о том, какие из
многочленов являются примитивными, что
позволяет избежать возможных затруднений
в определении примитивных элементов
поля. В табл. 5.4 приведены примитивные
многочлены над 
 для 
 от
1 до 20 [3, 30].

Помимо
представленных в таблице примитивными
являются также полиномы, векторы
коэффициентов которых написаны в
обратном порядке. Такие полиномы
называются двойственными, или взаимными
исходным.

Таблица
5.4. Примитивные многочлены до степени 

Это
пары 
 и 
; 
 и 
 и
т.д. Использовавшийся ранее при
построении 
 полином 
 примитивен,
на основании чего в качестве примитивного
элемента поля был взят 
.

Изоморфизм
конечных полей

Расширение
конечного поля 
 может
быть задано разными полиномами одинаковых
степеней 
.
В каком соотношении находятся эти поля?
Прежде всего, очевидно, ненулевыми
элементами любого поля порядка 
 является
тот же полный набор всевозможных
многочленов степени 
 и
ниже, отличающийся для разных
полиномов 
 лишь
порядком следования элементов 
 по
степеням примитивного элемента.

В
теории конечных полей доказывается,
что все поля 
 одного
порядка 
 изоморфны
(«подобны по форме»), т.е. между 
 и 
 существует
взаимнооднозначное отображение 
 друг
на друга, сохраняющее операции сложения
и умножения. Это означает, что для любых
двух элементов 
 и 
 из 
 справедливы
соотношения


,

(5.12)


.

(5.13)

Нетрудно
убедиться, что между полями, построенными
на основе неприводимых полиномов 
 и 
 (табл.
5.2), существует взаимнооднозначное
отображение: 
.
Простой подстановкой можно убедиться,
что при таком отображении сохраняются
операции сложения и умножения (5.12) и
(5.13). Например, для сложения


,


.

Аналогично
для умножения


,


.

5.4.
Линейные блочные коды

5.4.1.
Система передачи дискретных сообщений

При
передаче информации по каналам связи
возможны ошибки вследствие помех и
искажений сигналов. Для обнаружения и
исправления возникающих ошибок
используются помехоустойчивые коды.
Упрощенная схема системы передачи
информации при помехоустойчивом
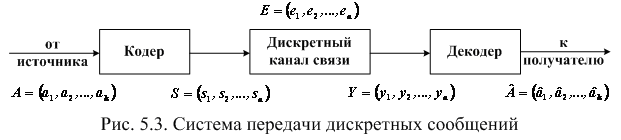
кодировании показана на рис. 5.3.

Кодер
служит для преобразования поступающей
от источника сообщений последовательности
из 
 информационных
символов в последовательность
из 
 символов
кодовых комбинаций (или кодовых слов).
Совокупность кодовых слов образует
код.

Множество
символов, из которых составляется
кодовое слово, называется алфавитом
кода, а число различных символов в
алфавите – основанием кода. В дальнейшем
вследствие их простоты и наибольшего
распространения рассматриваются главным
образом двоичные коды, алфавит которых
содержит два символа: 0 и 1.

Правило,
по которому информационной последовательности
сопоставляется кодовое слово, называется
правилом кодирования. Если при кодировании
каждый раз формируется блок 
 из 
 информационных
символов, превращаемый затем в 
-символьную
кодовую комбинацию 
,
то код называется блочным. При другом
способе кодирования информационная
последовательность на блоки не
разбивается, и код называется непрерывным.

С
математической точки зрения кодер
осуществляет отображение множества
из 
 элементов
(двоичных информационных последовательностей)
в множество, состоящее из 
 элементов
(двоичных последовательностей длины 
).
Для практики интересны такие отображения,
в результате которых получаются коды,
обладающие способностью исправлять
часть ошибок и допускающие простую
техническую реализацию кодирующих и
декодирующих устройств.

Дискретный
канал связи – это совокупность технических
средств вместе со средой распространения
радиосигналов, включенных между кодером
и декодером для передачи сигналов,
принимающих конечное число разных
видов. Для описания реальных каналов
предложено много математических моделей,
с разной степенью детализации отражающих
реальные процессы. Ограничимся
рассмотрением простейшей модели
двоичного канала, входные и выходные
сигналы которого могут принимать
значения 0 и 1.

Наиболее
распространено предположение о действии
в канале аддитивной помехи.
Пусть 
 и 
 соответственно
входная и выходная последовательности
двоичных символов. Помехой или вектором
ошибки называется последовательность
из 
 символов 
,
которую надо поразрядно сложить с
переданной последовательностью, чтобы
получить принятую:


.

(5.14)

Таким
образом, компонента вектора
ошибки 
 указывает
на то, что 2-й символ принят правильно
(
),
а компонента 
 указывает
на ошибку при приеме (
).Поэтому
важной характеристикой вектора ошибки
является число 
 ненулевых
компонентов, которое называется весом
или кратностью ошибки. Кратность ошибки
– дискретная случайная величина,
принимающая целочисленные значения от
0 до 
.

Классификация
двоичных каналов ведется по виду
распределения случайного вектора 
.
Основные результаты теории кодирования
получены в предположении, что вероятность
ошибки в одном символе не зависит ни от
его номера в последовательности, ни от
его значения. Такой канал называется
стационарным и симметричным. В этом
канале передаваемые символы искажаются
с одинаковой вероятностью 
,
т.е. 
, 
.

Для
симметричного стационарного канала
распределение вероятностей векторов
ошибки кратности 
 является
биноминальным:


,

где    
 –
число сочетаний из 
 элементов
по 
.

Вероятность
искажения конкретных 
 символов
(или вероятность появления одной
конфигурации 
 вектора
ошибки веса 
)
определяется по формуле


,

которая
показывает, что при 
 вероятность 
 является
убывающей функцией 
,
т.е. в симметричном стационарном канале
более вероятны ошибки меньшей кратности.
Этот важный факт используется при
построении помехоустойчивых кодов,
т.к. позволяет обосновать тактику
обнаружения и исправления в первую
очередь ошибок малой кратности. Конечно,
для других моделей канала такая тактика
может и не быть оптимальной.

Декодирующее
устройство (декодер) предназначено
оценить по принятой последовательности 
 значения
информационных символов 
.
Из-за действия помех возможны неправильные
решения. Процедура декодирования
включает решение двух задач: оценивание
переданного кодового слова и формирование
оценок информационных символов.

Вторая
задача решается относительно просто.
При наиболее часто используемых
систематических кодах, кодовые слова
которых содержат информационные символы
на известных позициях, все сводится к
простому их стробированию. Очевидно
также, что расположение информационных
символов внутри кодового слова не имеет
существенного значения. Удобно считать,
что они занимают первые 
 позиций
кодового слова.

Наибольшую
трудность представляет первая задача
декодирования. При равновероятных
информационных последовательностях
ее оптимальное решение дает метод
максимального правдоподобия. Функция
правдоподобия как вероятность получения
данного вектора 
 при
передаче кодовых слов 
, 
 на
основании (5.14) определяется вероятностями
появления векторов ошибок:


,

где    
 –
вес вектора 

Очевидно,
вероятность 
 максимальна
при минимальном 
.
На основании принципа максимального
правдоподобия оценкой 
 является
кодовое слово, искажение которого для
превращения его в принятое слово 
 имеет
минимальный вес, т. е. в симметричном
канале является наиболее вероятным
(НВ):


.

Если
несколько векторов ошибок 
 имеют
равные минимальные веса, то наивероятнейшая
ошибка 
 определяется
случайным выбором среди них.

В
качестве расстояния между двумя кодовыми
комбинациями принимают так называемое
расстояние Хэмминга, которое численно
равно количеству символов, в которых
одна комбинация отлична от другой, т.е.
весу (числу ненулевых компонентов)
разностного вектора. Расстояние Хэмминга
между принятой последовательностью 
 и
всеми возможными кодовыми словами 5,
есть функция весов векторов ошибок 
:


.

Поэтому
декодирование по минимуму расстояния,
когда в качестве оценки берется слово,
ближайшее к принятой последовательности,
является декодированием по максимуму
правдоподобия.

Таким
образом, оптимальная процедура
декодирования для симметричного канала
может быть описана следующей
последовательностью операций. По
принятому вектору 
 определяется
вектор ошибки с минимальным весом 
,
который затем вычитается (в двоичном
канале — складывается по модулю 2) из 
:


.

Наиболее
трудоемкой операцией в этой схеме
является определение наи-вероятнейшего
вектора ошибки, сложность которой
существенно возрастает при увеличении
длины кодовых комбинаций. Правила
кодирования, которые нацелены на
упрощение процедур декодирования,
предполагают придание всем кодовым
словам технически легко проверяемых
признаков.

Широко
распространены линейные коды, называемые
так потому, что их кодовые слова образуют
линейное подпространство над конечным
полем. Для двоичных кодов естественно
использовать поле характеристики 
.
Принадлежность принятой комбинации 
 известному
подпространству является тем признаком,
по которому выносится решение об
отсутствии ошибок (
).

Так
как по данному коду все пространство
последовательностей длины 
 разбивается
на смежные классы (см. 5.3.2), то для каждого
смежного класса можно заранее определить
вектор ошибки минимального веса,
называемый лидером смежного класса.
Тогда задача декодера состоит в
определении номера смежного класса,
которому принадлежит 
,
и формировании лидера этого класса.

Источник

Вектор
ош. – двоичн.
кодовое слово такой же длины как исходное,
содержащее ед-цы в тех разрядах, где
произошло искажение содержимого код.
слова. (код. слово и вектор ош. — абстракция).
Воздействие помехи на слово заменяется
слож-ем по mod2
исходн. слова с вектором ош.

Ошибки
различают на некорректируемые и
корректируемые.

Некорректир
– при которых изменение содержимого в
каком-то разряде слова не влияет на
искажение содержимого в других словах.

При
корректир – изменение содержимого под
влиянием помех влечёт искажение
содержимого некоторых других разрядах.

Различают
ош. разной кратности:

1)однократные,

2)двукратные,

3)r-кратные
(одновременное искажение содержимого
в r-
разрядах).

Однократная
ошибка вызывает искажение содержимого
только 1 разряда слова и т.д.

Вероятность
r-кратной
ошибки в n-разрядном
слове:

-кол-во
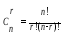
таких ошибок

Вероятность
такого события – вероятность сложного
события и определяется произведение
следующих множителей: вероятности, что
искажение произойдет в этом разряде p,
т.к. таких разрядов r
и события независимые, то — pr
, вероятности,
что в остальных (n-r)
разрядах искажения не будет определяется
как (1-p)(n—r)
, умноженных на количество возможных
r-кратных
ошибок. Т.о.

P=

17. Формулы для определения числа избыточных разрядов и границы Хэмминга для оптимальных корректирующих кодов; их суть и связь, примеры использования.

Пусть
имеем n-разр.
слова, требуется исправлять ошибкки
вплоть до кратности S.
Определим, какое мн-во разреш-х код. слов
можно выделить на мн-ве всех n-разр-х
слов. Для каждой исправляемой ош-ки.
соотв-щее ей запрещ. код. слово. Поэтому
«вокруг» каждого разреш. слова должны
сгруппироваться те запрещ. слова, ош-ки
кот-х подлежат исправлению. Поэтому
кол-во запрещ. слов. не <, чем число
исправл-ых ошибок.

2k-1>=Q
– определяется число информационных
разрядов; 2n—k-1>=n
– определяется число разрядов
помехоустойчивого слова; n-k=m
— определяется число избыточных разрядов;
– определяется граница Хемминга.
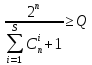
Дополнительных разрядов в кодовом слове
должно быть столько, чтобы породить
нужное число запрещенных слов или
классов смежности, а именно 2n—k-1.
Число классов смежности должно быть не
меньше, чем число исправляемых ошибок,
поэтому – 2n—k-1>=n

Пример:
 Пусть для
построения кода, корректирующего все
однократные ошибки, используются
однобайтовые слова. Требуется определить
максимальное число разрешенных слов,
выбираемых из всего множества однобайтовых
слов.

Число
однократных ошибок
,
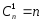
т.е.
.

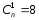
Максимальное
число разрешенных слов
,т.е.

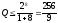
18. Построение группового корректирующего кода (на примере).

Пример:

тип
исправляемых ошибок — некоррелированные;

кратность
— S
= 1,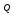=15.

Процедура
состоит из четырех этапов.

1.
Расчет числа информационных и избыточных
разрядов:

;

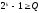
k
= 4;

n
= 7;

n
— k
=3;

где
k
— число информационных разрядов;

n
— число
избыточных разрядов;

2.
Построение таблицы опознавателей
ошибок.

Каждой
ошибке соответствует собственный
опознаватель.

Векторы
ошибок

а7
а6 а5 а4 а3 а2 а1

опознаватели

(данный
код) код Хемминга

1
0 0 0 0 0 0

111

0
1 0 0 0 0 0

110

0
0 1 0 0 0 0

101

0
0 0 1 0 0 0

100

0
0 0 0 1 0 0

011

0
0 0 0 0 1 0

010

0
0 0 0 0 0 1

001

n
= 7 n
— k
=3

3.
Определение проверочных равенств.

1
— й (младший) — а1
а3 
а6 
а7 ;

2
— й — а2 
а5 
а6 
а7 ;

3
— й — а1 
а2 
а4 
а7 ;

При
отсутствии однократных ошибок в слове
дешифратор вычислит нулевой
— опознаватель
(состоящий из одних нулей — 000). Поэтому
можно записать проверочные
равенства
дешифратора в виде следующей системы
уравнений.

—
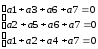
уравнения, формирующие 1-ый, 2-ой и 3-ий
разряды опознавателя.

4.
Построение алгоритма кодирования.

Имея
данную систему уравнений на роль
избыточных разрядов следует выбирать
те, которые встречаются в проверочных
равенствах по одному разу, т.е.
.
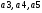
Выделение избыточных разрядов
сопровождается определением информационных
разрядов помехоустойчивого кодового
слова. При этом для данного кода будут
помечены правила кодирования в виде:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #

From Wikipedia, the free encyclopedia

The error vector magnitude or EVM (sometimes also called relative constellation error or RCE) is a measure used to quantify the performance of a digital radio transmitter or receiver. A signal sent by an ideal transmitter or received by a receiver would have all constellation points precisely at the ideal locations, however various imperfections in the implementation (such as carrier leakage, low image rejection ratio, phase noise etc.) cause the actual constellation points to deviate from the ideal locations. Informally, EVM is a measure of how far the points are from the ideal locations.

Noise, distortion, spurious signals, and phase noise all degrade EVM, and therefore EVM provides a comprehensive measure of the quality of the radio receiver or transmitter for use in digital communications. Transmitter EVM can be measured by specialized equipment, which demodulates the received signal in a similar way to how a real radio demodulator does it. One of the stages in a typical phase-shift keying demodulation process produces a stream of I-Q points which can be used as a reasonably reliable estimate for the ideal transmitted signal in EVM calculation.

Definition[edit]

Constellation diagram and EVM

An error vector is a vector in the I-Q plane between the ideal constellation point and the point received by the receiver. In other words, it is the difference between actual received symbols and ideal symbols. The root mean square (RMS) average amplitude of the error vector, normalized to ideal signal amplitude reference, is the EVM. EVM is generally expressed in percent by multiplying the ratio by 100. [1]

The ideal signal amplitude reference can either be the maximum ideal signal amplitude of the constellation, or it can be the root mean square (RMS) average amplitude of all possible ideal signal amplitude values in the constellation. For many common constellations including BPSK, QPSK, and 8PSK, these two methods for finding the reference give the same result, but for higher-order QAM constellations including 16QAM, Star 32QAM, 32APSK, and 64QAM the RMS average and the maximum produce different reference values. [2]

The error vector magnitude is sometimes expressed in dB. This is related to the value of EVM in percent as follows:

{displaystyle mathrm {EVM} _{text{dB}}=20log _{10}left({mathrm {EVM} _{%} over 100}right).}

The definition of EVM depends heavily on the standard that is being used, for example in 3GPP LTE the relevant documents will define exactly how EVM is to be measured. There are discussions ongoing by academics as to some of the problems around EVM measurement.[3]

Dynamic EVM[edit]

Battery life and power consumption are important considerations for a system-level RF transmitter design. Because the transmit power amplifier (PA) consumes a significant portion of the total system DC power, a number of techniques are employed to reduce PA power usage. Many PAs offer an adjustable DC supply voltage to optimize the maximum RF output power level versus its DC power consumption. Also, most PAs can be powered-down or disabled when not in use to conserve power, such as while receiving or between packets during transmission. In order to maximize power efficiency, the PA must have fast turn-on and turn-off switching times. The highest DC power efficiency occurs when the time delta between PA Enable and the RF signal is minimized, but a short delay can exacerbate transient effects on the RF signal.

Because the power-up/power-down operation of the PA can cause transient and thermal effects that degrade transmitter performance, another metric called Dynamic EVM is often tested. Dynamic EVM is measured with a square wave pulse applied to PA Enable to emulate the actual dynamic operation conditions of the transmitter. The degradation in dynamic EVM is due to the PA transient response affecting the preamble at the start of the packet and causing an imperfect channel estimate. Studies have shown that dynamic EVM with a 50% duty cycle square wave applied to PA Enable to be worse than the static EVM (PA Enable with 100% duty cycle).[4]

See also[edit]

  • Modulation error ratio
  • Carrier to Noise Ratio
  • Signal-to-noise ratio

References[edit]

  1. ^ «Error Vector Magnitude (Digital Demodulation)».
  2. ^ «EVM Normalization Reference (Digital Demod)».
  3. ^ Vigilante, McCune, Reynaert. «To EVM or Two EVMs?». doi:10.1109/MSSC.2017.2714398. S2CID 6849707. CS1 maint: multiple names: authors list (link)
  4. ^ Power Amplifier Testing For 802.11ac

From Wikipedia, the free encyclopedia

The error vector magnitude or EVM (sometimes also called relative constellation error or RCE) is a measure used to quantify the performance of a digital radio transmitter or receiver. A signal sent by an ideal transmitter or received by a receiver would have all constellation points precisely at the ideal locations, however various imperfections in the implementation (such as carrier leakage, low image rejection ratio, phase noise etc.) cause the actual constellation points to deviate from the ideal locations. Informally, EVM is a measure of how far the points are from the ideal locations.

Noise, distortion, spurious signals, and phase noise all degrade EVM, and therefore EVM provides a comprehensive measure of the quality of the radio receiver or transmitter for use in digital communications. Transmitter EVM can be measured by specialized equipment, which demodulates the received signal in a similar way to how a real radio demodulator does it. One of the stages in a typical phase-shift keying demodulation process produces a stream of I-Q points which can be used as a reasonably reliable estimate for the ideal transmitted signal in EVM calculation.

Definition[edit]

Constellation diagram and EVM

An error vector is a vector in the I-Q plane between the ideal constellation point and the point received by the receiver. In other words, it is the difference between actual received symbols and ideal symbols. The root mean square (RMS) average amplitude of the error vector, normalized to ideal signal amplitude reference, is the EVM. EVM is generally expressed in percent by multiplying the ratio by 100. [1]

The ideal signal amplitude reference can either be the maximum ideal signal amplitude of the constellation, or it can be the root mean square (RMS) average amplitude of all possible ideal signal amplitude values in the constellation. For many common constellations including BPSK, QPSK, and 8PSK, these two methods for finding the reference give the same result, but for higher-order QAM constellations including 16QAM, Star 32QAM, 32APSK, and 64QAM the RMS average and the maximum produce different reference values. [2]

The error vector magnitude is sometimes expressed in dB. This is related to the value of EVM in percent as follows:

{displaystyle mathrm {EVM} _{text{dB}}=20log _{10}left({mathrm {EVM} _{%} over 100}right).}

The definition of EVM depends heavily on the standard that is being used, for example in 3GPP LTE the relevant documents will define exactly how EVM is to be measured. There are discussions ongoing by academics as to some of the problems around EVM measurement.[3]

Dynamic EVM[edit]

Battery life and power consumption are important considerations for a system-level RF transmitter design. Because the transmit power amplifier (PA) consumes a significant portion of the total system DC power, a number of techniques are employed to reduce PA power usage. Many PAs offer an adjustable DC supply voltage to optimize the maximum RF output power level versus its DC power consumption. Also, most PAs can be powered-down or disabled when not in use to conserve power, such as while receiving or between packets during transmission. In order to maximize power efficiency, the PA must have fast turn-on and turn-off switching times. The highest DC power efficiency occurs when the time delta between PA Enable and the RF signal is minimized, but a short delay can exacerbate transient effects on the RF signal.

Because the power-up/power-down operation of the PA can cause transient and thermal effects that degrade transmitter performance, another metric called Dynamic EVM is often tested. Dynamic EVM is measured with a square wave pulse applied to PA Enable to emulate the actual dynamic operation conditions of the transmitter. The degradation in dynamic EVM is due to the PA transient response affecting the preamble at the start of the packet and causing an imperfect channel estimate. Studies have shown that dynamic EVM with a 50% duty cycle square wave applied to PA Enable to be worse than the static EVM (PA Enable with 100% duty cycle).[4]

See also[edit]

  • Modulation error ratio
  • Carrier to Noise Ratio
  • Signal-to-noise ratio

References[edit]

  1. ^ «Error Vector Magnitude (Digital Demodulation)».
  2. ^ «EVM Normalization Reference (Digital Demod)».
  3. ^ Vigilante, McCune, Reynaert. «To EVM or Two EVMs?». doi:10.1109/MSSC.2017.2714398. S2CID 6849707. CS1 maint: multiple names: authors list (link)
  4. ^ Power Amplifier Testing For 802.11ac

Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.

Давайте же разберёмся, что это такое.

Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.

Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.

Каналы с ошибкой

Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.

Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем $k$ ошибок. Это будет характеристикой канала связи.

Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами ($A$, $B$, $C$, …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.

Кодирование и декодирование будем обозначать прямой стрелкой ($rightarrow$), а передачу по каналу связи — волнистой стрелкой ($rightsquigarrow$). Ошибки при передаче будем подчёркивать.

Например, пусть мы хотим передавать только сообщения $A=0$ и $B=1$. В простейшем случае их можно закодировать нулём и единицей (сюрприз!):

$ begin{aligned} A &to 0, B &to 1. end{aligned} $

Передача по каналу, в котором возникла ошибка будет записана так:

$ A to 0 rightsquigarrow underline{1} to B. $

Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это $0$ и $1$.

Код с утроением

Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:

$ begin{aligned} A &to 00, B &to 11. end{aligned} $

Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:

$ A to 00 rightsquigarrow 0underline{1} to ?. $

Какие выводы мы можем сделать, когда получили $01$? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква $B$. А может, во втором, и была передана $A$.

То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.

$ begin{aligned} A &to 000, B &to 111. end{aligned} $

Проверим в деле:

$ A to 000 rightsquigarrow 0underline{1}0 to A?. $

Получили $010$. Тут у нас есть две возможности: либо это $B$ и было две ошибки (в крайних цифрах), либо это $A$ и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква $A$. Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.

Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква $A$.

Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.

Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.

Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.

Расстояния между кодами

Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.

И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.

Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.

Пусть мы передавали $000$, а получили $001$. Видно, что эта цепочка больше похожа на исходные $000$, чем на $111$. А так как других кодовых слов у нас нет, то и выбор очевиден.

Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.

Можно ввести некоторую величину $d(alpha, beta)$, равную количеству различающихся цифр в соответствующих разрядах цепочек $alpha$ и $beta$. Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.

Например, $d(010, 010) = 0$, так как все цифры в соответствующих позициях равны, а вот $d(010101, 011011) = 3$.

Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:

  1. Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
  2. Расстояние в обе стороны одинаково.
  3. Путь через третью точку не короче, чем прямой путь.

Достаточно разумные требования.

Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):

  1. $d(x, y) geqslant 0,quad d(x, y) = 0 Leftrightarrow x = y;$
  2. $d(x, y) = d(y, x);$
  3. $d(x, z) + d(z, y) geqslant d(x, y)$.

Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.

Окрестности

Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.

Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.

Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.

Так, скажем, окрестность кодового слова $000$ радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:

$ {000, 100, 010, 001}. $

Да, вот так странно выглядят шары в пространстве кодов.

А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим $000$! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.

Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение $x$, мы получим один из кодов, который принадлежит окрестности $x$ радиусом 2.

Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.

Сколько ошибок может исправить код?

Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.

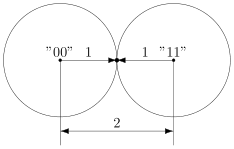
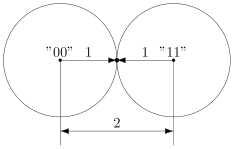
В коде с удвоением между кодовыми словами $00$ и $11$ расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.

Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.

Что интересно, точек касания в нашем странном пространстве у шаров две — это коды $01$ и $10$. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.

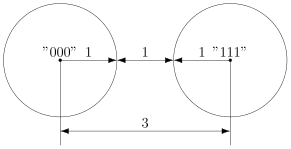
В случае кода с утроением, между шарами будет зазор.

Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).

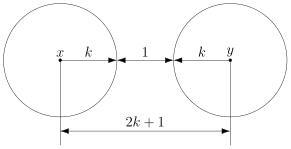
В общем случае получаем следующее.

Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием $d_{min}$ будет успешно работать в канале с $k$ ошибками, если выполняется соотношение

$ d_{min} geqslant 2k+1. $

Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает $k$ ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса $k$ других кодовых слов. Математически это записывается так:

$d_{min}geqslant k + 1.$

Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.

$ begin{aligned} A to 10100, B to 01000, C to 00111, D to 11011. end{aligned} $

Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.

A B C D
A — 3 3 4
B 3 — 4 3
C 3 4 — 3
D 4 3 3 —

Минимальное расстояние $d_{min}=3$, а значит $3geqslant2k+1$, откуда получаем, что такой код может исправить до $k=1$ ошибок. Обнаруживает же он две ошибки.

Рассмотрим пример:

$ A to 10100 rightsquigarrow 101underline{1}0. $

Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.

$ begin{aligned} A:, d(10110, 10100) &= 1, B:, d(10110, 01000) &= 4, C:, d(10110, 00111) &= 2, D:, d(10110, 11011) &= 3. end{aligned} $

Минимальное расстояние получилось для символа $A$, значит вероятнее всего передавался именно он:

$ A to 10100 rightsquigarrow 101underline{1}0 to A?. $

Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.

Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.

Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы $2^5 = 32$ варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.

Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.

Интерлюдия: поле GF(2)

Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.

Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):

$ begin{aligned} 0 + 0 &= 0, 0 + 1 &= 1, 1 + 0 &= 1, 1 + 1 &= 0. end{aligned} $

Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.

Множество из двух элементов ${0, 1}$ с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.

У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.

$ x + x = 0. $

Это свойство прямо следует из определения.

$ x + y = x - y. $

А в этом можно убедиться, прибавив $y$ к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.

Проверяем корректность

Вернёмся к коду с утроением.

$ begin{aligned} A &to 000, B &to 111. end{aligned} $

Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.

Пусть мы приняли вектор-строку $x$ из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)

$dots rightsquigarrow x = (x_1, x_2, x_3). $

Математически равенство всех трёх цифр можно записать как систему:

$ left{ begin{aligned} x_1 &= x_2, x_2 &= x_3. end{aligned} right. $

Или, если воспользоваться свойствами сложения в GF(2), получаем

$ left{ begin{aligned} x_1 + x_2 &= 0, x_2 + x_3 &= 0. end{aligned} right. $

Или

$ left{ begin{aligned} 1cdot x_1 + 1cdot x_2 + 0cdot x_3 &= 0, 0cdot x_1 + 1cdot x_2 + 1cdot x_3 &= 0. end{aligned} right. $

В матричном виде эта система будет иметь вид

$ Hx^T = 0, $

где

$ H = begin{pmatrix} 1 & 1 & 0 0 & 1 & 1 end{pmatrix}. $

Транспонирование здесь нужно потому, что $x$ — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.

Будем называть матрицу $H$ проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.

Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.

Кодирование

Итак, у нас есть система для проверки

$ left{ begin{aligned} x_1 + x_2 &= 0, x_2 + x_3 &= 0. end{aligned} right. $

Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице $H$) найдём кодовые слова.

Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:

$ H = begin{pmatrix} 1 & 0 & 1 & 0 & 0 0 & 1 & 1 & 0 & 1 0 & 0 & 0 & 1 & 1 end{pmatrix}. $

Соответствующая система имеет вид:

$ left{ begin{aligned} x_1 + x_3 &= 0, x_2 + x_3 + x_5 &= 0, x_4 + x_5 &= 0. end{aligned} right. $

Чтобы найти кодовые слова соответствующего кода нужно её решить.

В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если $a$ и $b$ — решения системы, то для их суммы верно

$H(a+b)^T=Ha^T+Hb^T=0+0=0,$

что означает, что она тоже — решение.

Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.

Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить $x_1, x_2, x_4$.

Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.

Итак, получаем:

$ left{ begin{aligned} x_1 &= x_3, x_2 &= x_3 + x_5, x_4 &= x_5. end{aligned} right. $

Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.

$ begin{aligned} x_3=1, x_5=0:quad x_1=1, x_2=1, x_4=0 Rightarrow x^{(1)} = (1, 1, 1, 0, 0), x_3=0, x_5=1:quad x_1=0, x_2=1, x_4=1 Rightarrow x^{(2)} = (0, 1, 0, 1, 1). end{aligned} $

Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:

$ a_1 x^{(1)}+a_2 x^{(2)}, $

где $a_1, a_2$ равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно $2^2=4$ сочетания.

Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.

$ (a_1, a_2)cdot begin{pmatrix} 1 & 1 & 1 & 0 & 0 0 & 1 & 0 & 1 & 1 end{pmatrix} = aG. $

Строчки здесь — линейно независимые решения, которые мы получили. Матрица $G$ называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:

$ a to aG. $

Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)

$ begin{aligned} 00 &to 00000, 01 &to 01011, 10 &to 11100, 11 &to 10111. end{aligned} $

Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?

$ a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to Hx^T = (110)^T neq 0. $

А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!

Для кода с утроением, кстати, порождающая матрица выглядит очень просто:

$G=begin{pmatrix}1&1&1end{pmatrix}.$

Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.

Ошибка по синдрому

Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!

Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение $x$, а было отправлено кодовое слово $v$. Тогда вектор ошибки по определению

$ e = x - v. $

Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:

$ begin{aligned} v &= x + e, x &= v + e. end{aligned} $

В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.

Как мы уже говорили раньше, если мы получили сообщение $x$ с ошибкой, то $Hx^Tneq 0$. Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?

Назовём результат умножения на проверочную матрицу синдромом:

$ s(x)=Hx^T.$

И заметим следующее

$ s(x) = Hx^T = H(v+e)^T = He^T = s(e). $

Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.

Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?

А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.

Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.

$s(x)$ $x$
$000$ $underline{00000}, 11100, 01011, 10111$
$001$ $underline{00010}, 11110, 01001, 10101$
$010$ $underline{01000}, 10100, 00011, 11111$
$011$ $01010, 10110, underline{00001}, 11101$
$100$ $underline{10000}, 01100, 11011, 00111$
$101$ $underline{10010}, 01110, 11001, underline{00101}$
$110$ $11000, underline{00100}, 10011, 01111$
$111$ $11010, underline{00110}, underline{10001}, 01101$

В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.

Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.

Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.

$ a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to s(x)=Hx^T = (110)^T to e=(00100). $

Вектор ошибки равен $(00100)$, а значит ошибка в третьем разряде. Как мы и загадали.

Ура, всё работает!

Что же дальше?

Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.

Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.

Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.

Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.

Э. Акар, Analog Devices, специалист по измерениям радиочастотных систем

Как измерение модуля вектора ошибки помогает оптимизировать общие характеристики системы

Статья опубликована в журнале Электроника НТБ № 8 2021

Модуль вектора ошибки (Error Vector Magnitude, EVM) — широко применяемый показатель системного уровня, который регламентируется различными стандартами в области связи для испытаний на соответствие в таких приложениях, как беспроводные локальные сети (WLAN 802.11), мобильная связь (4G LTE, 5G) и многие другие. Кроме того, это чрезвычайно важная системная характеристика, позволяющая количественно оценить совокупное влияние всех возможных проблем в системе с помощью одного, простого для понимания параметра. В статье проанализировано, как характеристики более низкого уровня влияют на EVM, рассмотрен ряд практических примеров использования EVM для оптимизации характеристик устройства на уровне системы, показано, как добиться снижения EVM на 15 дБ по сравнению с требованиями большинства стандартов связи.

Большинство инженеров, работающих в области радиочастотных систем, оперируют такими характеристиками, как коэффициент шума, точка пересечения третьего порядка и отношение сигнал — шум. Понимание совокупного влияния этих параметров на общие рабочие характеристики системы может быть сложной задачей. Модуль вектора ошибки позволяет быстро получить представление о работе системы в целом, вместо того, чтобы оценивать несколько разных показателей.

Что такое модуль вектора ошибки?
EVM — это простой показатель для количественной оценки комбинации всех искажений сигнала в системе. Он часто определяется для устройств, использующих цифровую модуляцию, которая может быть представлена в виде графика синфазных (I) и квадратурных (Q) векторов, известного также как «диаграмма созвездия» (constellation diagram) (рис. 1a). Как правило, EVM вычисляется путем нахождения идеального местоположения созвездия для каждого принятого символа, как показано на рис. 1б. Среднеквадратичное значение всех модулей вектора ошибки между местоположениями принятых символов и их ближайшими идеальными местоположениями в созвездии определяет величину EVM устройства [1].

Рис. 1. а — диаграмма созвездия и граница принятия решения; б — вектор ошибки между принятым символом и идеальным местоположением символа

В стандарте IEEE 802.11 приведена формула для вычисления EVM [2]:

где: Lp — количество кадров, Nc — количество несущих, Ri, j — принятый символ, а Si, j — идеальное местоположение символа.
EVM тесно связан с частотой битовых ошибок (BER) данной системы. Когда принятые символы располагаются далеко от целевой точки созвездия, вероятность их попадания в границу принятия решения другой точки созвездия увеличивается. Это приводит к увеличению BER. Важное различие между BER и EVM состоит в том, что BER для переданного сигнала вычисляется на основе переданной битовой комбинации, в то время как EVM вычисляется на основе расстояния от ближайшей точки созвездия символов до местоположения символа. В некоторых случаях символы могут пересекать границу принятия решения, и им присваивается неправильная битовая комбинация. Если символ попадает ближе к другому идеальному местоположению символа, это может улучшить EVM для этого символа. Таким образом, хотя EVM и BER тесно связаны, эта связь может быть нарушена при очень высоких уровнях искажения сигнала.
Современные стандарты в области связи устанавливают минимально допустимый уровень EVM на основе характеристик передаваемого или принятого сигнала, таких как скорость передачи данных и полоса пропускания. Устройства, которые достигают целевого уровня EVM, соответствуют стандарту, в то время как устройства, которые не достигают целевого уровня EVM, не соответствуют его требованиям. Испытательное и измерительное оборудование, предназначенное для проверки на соответствие стандартам, обычно ориентировано на более строгие целевые значения EVM, которые могут быть на порядок ниже требуемых в стандарте. Это позволяет оборудованию определять EVM тестируемого устройства без значительных искажений сигнала.

Что влияет на EVM?
Как показатель ошибки, EVM тесно связан со всеми источниками искажений в системе. Мы можем количественно оценить влияние всех отклонений в системе на EVM, вычислив, как они искажают принимаемые и передаваемые сигналы. Проанализируем влияние нескольких ключевых видов помех, таких как тепловой шум, фазовый шум и нелинейности, на EVM.

Белый шум
Белый шум присутствует во всех радиочастотных системах. Когда шум является единственным искажением в системе, результирующий EVM можно рассчитать по следующей формуле:

где SNR — отношение сигнал — шум системы в дБ, а PAPR — отношение пиковой мощности к средней мощности данного сигнала в дБ.
Обратите внимание, что SNR обычно определяется для однотонального сигнала. Для модулированного сигнала необходимо учитывать PAPR сигнала. Поскольку PAPR однотонального сигнала составляет 3 дБ, это число необходимо вычесть из значения SNR для сигнала с произвольным значением PAPR.
Для высокоскоростных АЦП и ЦАП, уравнение 2 может быть выражено через спектральную плотность шума (NSD):

где NSD — спектральная плотность шума в дБ ПШ / Гц, BW — ширина полосы сигнала в Гц, PAPR — отношение пиковой мощности к средней, а Pbackoff — разница между пиковой мощностью сигнала и полным диапазоном измерений преобразователя.
Эта формула может быть очень удобна для прямого расчета ожидаемого значения EVM устройства с использованием значения NSD, которое обычно указывается для современных высокоскоростных преобразователей. Обратите внимание, что для высокоскоростных преобразователей необходимо учитывать также шум квантования. Величина NSD большинства высокоскоростных преобразователей также включает шум квантования. Следовательно, для этих устройств уравнение 3 отражает не только тепловой шум, но также шум квантования.
Как показывают эти два уравнения, EVM сигнала напрямую зависит от общей полосы пропускания сигнала, отношения пиковой мощности к средней и теплового шума системы.

Как фазовый шум влияет на EVM
Другим видом шума, который влияет на EVM системы, является фазовый шум, который представляет собой случайные флуктуации фазы и частоты сигнала [3]. Все нелинейные элементы схемы вносят фазовый шум. Основные источники фазового шума в данной системе могут быть прослежены вплоть до генераторов. Генератор частоты дискретизации преобразователя данных, используемый для преобразования частоты гетеродин и генератор опорной частоты — все эти устройства могут вносить вклад в общий фазовый шум системы.
Ухудшение характеристик из-за фазового шума зависит от частоты. Для типичного генератора большая часть энергии несущей приходится на его основную частоту генерации, которая называется центральной частотой. Часть энергии сигнала будет распределяться около этой центральной частоты. Отношение амплитуды сигнала в полосе частот 1 Гц при определенном сдвиге частоты к его амплитуде на центральной частоте определяется как фазовый шум при этом конкретном частотном сдвиге, как показано на рис. 2.

Фазовый шум системы напрямую влияет на ее EVM. EVM из-за фазового шума системы можно рассчитать путем интегрирования фазового шума в полосе пропускания. Для большинства современных стандартов связи, в которых используется ортогональная частотная модуляция (OFDM), фазовый шум должен быть интегрирован в диапазоне от примерно 10% разнесения поднесущих до полной ширины полосы сигнала:

где L — плотность фазового шума в одиночной боковой полосе, fsc — разнесение поднесущих, BW — ширина полосы сигнала.
Большинство устройств, генерирующих частоту, имеют низкий фазовый шум на частотах <2 ГГц с типичными уровнями интегрированного джиттера на несколько порядков ниже предельных значений EVM, устанавливаемых в стандартах. Однако для более высокочастотных и более широкополосных сигналов интегрированные уровни фазового шума могут быть значительно выше, что может привести к гораздо более высоким значениям EVM. Обычно это относится к устройствам миллиметрового диапазона, которые работают на частотах выше 20 ГГц. Как мы подробнее обсудим в разделе, посвящен ном описанию примеров проектов, фазовый шум следует рассчитывать для всей системы, чтобы достичь наименьшего общего EVM.

Расчет влияния нелинейностей на EVM
Нелинейности системного уровня приводят к появлению интермодуляционных составляющих, которые могут попадать в полосу пропускания сигнала. Эти помехи могут перекрываться с поднесущими, воздействуя на их амплитуду и фазу. Можно вычислить вектор ошибки, возникающий из-за интермодуляционных помех. Выведем простую формулу для расчета EVM системы из-за интермодуляционных составляющих третьего порядка.

Рис. 3. Интермодуляционные составляющие OFDM-сигнала

Как показано на рис. 3a, двухтональный сигнал создает две интермодуляционные составляющие. Мощность интермодуляционных составляющих можно рассчитать следующим образом:

где Ptone — мощность тестового сигнала, OIP3 — точка пересечения третьего порядка на выходе, Pe — сигнал ошибки, представляющий собой разность мощностей основной частоты и интермодуляционной составляющей.
Для OFDM-сигнала с N тонами, как показано на рис. 3б, уравнение 6 принимает следующий вид:

где Pe, i — ошибка для каждой пары тонов.
Поскольку в каждом местоположении поднесущей имеется N / 2 интермодуляционных составляющих, которые перекрываются, уравнение можно переписать как:

Общая ошибка, включая все местоположения поднесущих, становится равной:

Подставляя уравнение 6 в уравнение 8, EVM можно выразить следующим образом:

где PRMS — среднеквадратичное значение сигнала, C — константа, которая находится в диапазоне от 0 до 3 дБ в зависимости от схемы модуляции.
Как показывает уравнение 11, EVM уменьшается по мере увеличения OIP3 системы. Это ожидаемо, поскольку более высокое значение OIP3 обычно указывает на более линейную систему. Кроме того, когда среднеквадратичная мощность сигнала уменьшается, EVM уменьшается по мере уменьшения мощности нелинейных составляющих.

Оптимизация системных характеристик с помощью EVM
Обычно проектирование на уровне системы начинается с каскадного анализа, при котором низкоуровневые параметры функциональных блоков используются для определения общих характеристик системы, построенной на базе этих блоков. Существуют хорошо зарекомендовавшие себя аналитические формулы и инструменты, которые можно использовать для расчета этих параметров. Однако многие инженеры не знают, как правильно использовать инструменты каскадного анализа для проектирования полностью оптимизированных систем.
В качестве системной характеристики EVM предоставляет инженерам-разработчикам ценную информацию для оптимизации системы. Вместо того, чтобы рассматривать несколько параметров, разработчики получают возможность выбрать оптимальное среднеквадратичное
значение EVM и, тем самым, найти наилучшее проектное решение.

U-образная кривая EVM
Мы можем объединить все параметры системы в один график, учитывая вклад EVM каждого искажения в системе и уровень выходной мощности. На рис. 4 показана типичная U-образная кривая EVM для системы в зависимости от уровня рабочей мощности. При низких уровнях рабочей мощности EVM определяется шумовыми характеристиками системы. На высоких уровнях мощности на EVM влияют нелинейности в системе. Самый низкий уровень EVM для системы обычно определяется комбинацией всех источников ошибок, включая фазовый шум.
Мы можем найти суммарный EVM с помощью уравнения 12:

где EVMWN — вклад EVM, возникающий из-за белого шума, EVMPhN — вклад фазового шума, EVMlinearity — EVM, возникающий из-за нелинейных искажений. Для заданного уровня мощности сумма мощностей всех этих ошибок определяет общий уровень EVM в системе.

Рис. 4. U-образная кривая зависимости EVM от рабочей мощности

Наряду с уравнением 12, U-образная кривая может быть очень полезной для системной оптимизации, когда можно визуализировать комбинацию всех ошибок данной системы.

Пример проекта
Рассмотрим пример проектирования сигнальной цепочки, используя EVM в качестве системного показателя. В этом примере мы спроектируем передатчик миллиметрового диапазона с использованием РЧ ЦАП с дискретизацией, модулятора и генераторов частоты миллиметрового диапазона, а также других устройств формирования сигнала (рис. 5).

Рис. 5. Сигнальная цепь передатчика миллиметрового диапазона

В этой сигнальной цепи используется микросхема AD9082, которая содержит четыре ЦАП и два АЦП с частотой выборки 12 и 6 ГГц соответственно. Эти преобразователи с прямым РЧ-преобразованием обеспечивают гибкость проектного решения для сигнальной цепи миллиметрового диапазона и непревзойденную производительность. На рис. 6 показаны результаты измерения значения EVM для типовой микросхемы AD9082 с помощью 12‑разрядного АЦП AD9213, который обеспечивает скорость выборки 10 Гвыб / с. Кольцевой тест для этой схемы показал уровень EVM всего -62 дБ, что на 27 дБ ниже предельной допустимой величины, определяемой стандартом.

Рис. 6. Результаты измерения EVM для микросхемы AD9082 на промежуточной частоте 400 МГц для сигнала IEEE 802.11ax с полосой пропускания 80 МГц с модуляцией QAM‑1024

В этой схеме также используется интегрированный миллиметровый модулятор ADMV1013, который содержит ряд традиционных блоков сигнальной цепи, таких как умножители частоты, квадратурные смесители и усилители. Чтобы упростить фильтрацию, в этом проекте используется довольно сложная топология цепи промежуточной частоты, в которой на квадратурные смесители модуляторов подаются сигналы с фазой 90°. Это устраняет одну из боковых полос сигнала, преобразованного с повышением частоты, тем самым уменьшается сложность фильтрации по сравнению с преобразованием сигнала с двумя боковыми полосами.
Чтобы оптимизировать эту сигнальную цепь для получения наименьшего значения EVM, сначала проанализируем фазовый шум на уровне системы, затем найдем оптимальное соотношение шума и линейности и, наконец, соберем все функциональные блоки в одну систему.

Улучшение EVM путем оптимизации фазового шума
Как мы обсуждали ранее, фазовый шум всей системы может ограничивать возможность минимизации EVM на частотах миллиметрового диапазона. Проанализируем вклад фазового шума каждого каскада, чтобы убедиться, что выбраны наилучшие компоненты для данной сигнальной цепи. Компоненты, формирующие частоты в этой сигнальной цепи, — это ЦАП, который синхронизируется с помощью синтезатора, и гетеродин. Общий фазовый шум можно выразить следующим образом:

где LTx – общий фазовый шум передатчика, lIF – фазовый шум на выходе ЦАП, lLO – фазовый шум сигнала гетеродина.
Используемый в этом примере ЦАП AD9082 имеет исключительно низкий аддитивный фазовый шум. Общий фазовый шум на выходе, который представляет собой сигнал ПЧ, можно рассчитать по простой формуле:

где LCLK – интегрированный фазовый шум тактового сигнала, fIF – ПЧ-частота на выходе ЦАП, fCLK – частота выборки для ЦАП.
Чтобы выбрать компоненты минимальной сложности и с наименьшим фазовым шумом, проанализируем характеристики двух микросхем, рассматриваемых в качестве кандидатов на роль генератора тактовой частоты и источника сигнала гетеродина.

Рис. 7. Фазовый шум тактового сигнала и сигнала гетеродина для ADF4372 и ADF4401A

На рис. 7 показана характеристика фазового шума сигнала с одной боковой полосой для двух микросхем, наилучшим образом подходящих для использования в качестве синтезаторов частоты для этой сигнальной цепи. Интегрированный фазовый шум для сигнала 5G NR может быть рассчитан путем интегрирования фазового шума источников сигнала в полосе от 6 кГц до 100 МГц (табл. 1).

На типичных для этой сигнальной цепи промежуточных частотах как ADF4372, так и ADF4401A демонстрируют чрезвычайно низкие уровни интегрированного шума. Поскольку для ADF4372 требуется гораздо меньшая площадь печатной платы, это хороший выбор для формирования
частоты выборки для РЧ-преобразователя, который создает ПЧ-сигнал. Микросхема ADF4401A становится выбором для генератора сигнала гетеродина из-за присущего ей низкого начального фазового шума. На частоте 30 ГГц он примерно на 20 дБ ниже интегрированного шума для ADF4372. Такой низкий уровень шума гарантирует, что фазовый шум сигнала гетеродина не станет ограничивать общие показатели EVM для всей системы.
Используя уравнение 13, можно рассчитать общий EVMPhN из-за фазового шума:

Такой уровень модуля вектора ошибка из-за фазового шума более чем достаточен для измерения сигналов с EVM порядка -30 дБ, как определено стандартом для 5G NR.

Оптимизация соотношения шума и линейности
Одна из основных проблем при проектировании РЧ-систем — поиск оптимального соотношения шума и линейности. Улучшение одного из этих двух параметров обычно приводит к неоптимальной величине другого. Анализ EVM на уровне системы может быть очень полезным инструментом для улучшения характеристик системы в целом.

Рис. 8. Оптимизация соотношения шума и линейности системы

Рис. 8 иллюстрирует поиск оптимального соотношения шума и линейности для созданной нами сигнальной цепи. Каждая из кривых получена путем регулировки управляющего напряжения интегрированного усилителя. Для каждой кривой изменялся уровень выходной мощности ЦАП. Заметим, что по мере увеличения уровня мощности EVM уменьшается из-за увеличения общего отношения сигнал – шум системы. После определенного уровня мощности нелинейности всего тракта прохождения сигнала начинают ухудшать показатель EVM. Результирующая U-образная кривая EVM для данной конфигурации усилителя очень узкая.
Регулируя управляющее напряжение усилителя, мы можем перейти к другой кривой, на которой система имеет более низкий EVM. Пунктирная линия на рис. 8 отражает оптимизацию на уровне системы, которая может быть достигнута с помощью интегрированных усилителей микросхемы ADMV1013. Результирующая U-образная кривая после этой оптимизации становится намного шире, что обеспечивает сверхнизкий EVM в широком диапазоне уровней выходной мощности.

Заключение
В статье мы рассмотрели EVM в качестве системного показателя и обсудили, как с помощью EVM можно оптимизировать характеристики системы. Как мы показали, EVM – хороший индикатор многих проблем системного уровня. Все источники ошибок приводят к возникновению поддающегося измерению EVM, который можно использовать для оптимизации общих показателей системы. Мы продемонстрировали также, что с помощью новейших высокоскоростных преобразователей и интегрированных модуляторов миллиметрового диапазона можно достичь характеристик системы приборного уровня и значений EVM на порядки величин более низких по сравнению с требованиями стандартов в области связи.

ЛИТЕРАТУРА
1. Voelker K. M. Apply Error Vector Measurements in Communication Design. – Microwaves & RF, December 1995.
2. IEEE 802.11a‑1999. IEEE Standard for Telecommunications and Information Exchange Between Systems. LAN / MAN Specific Requirements. Part 11: Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications: High Speed Physical Layer in the 5 GHz Band. – IEEE Standard
Association, September 1999.
3. Kester W. MT‑008 Tutorial: Converting Oscillator Phase Noise to Time Jitter. – Analog Devices, Inc., 2009.

Если комбинации кода известны и
он используется для исправления ошибок, то способ разбиения множества U на подмножества Ai
определяется статистикой ошибок, возникающих в его комбинациях. Обычно это
разбиение выполняется так, чтобы минимизировать среднюю вероятность появления
ложной комбинации на входе декодера.

В дальнейшем будем рассматривать
только двоичные коды, как получившие наибольшее распространение.

20. Понятие «вектор ошибок»

Для удобства представления
ошибок, возникающих в комбинациях двоичного корректирующего кода, используется
понятие вектор ошибок. Под вектором ошибок понимается комбинация длины N символов с 2-мя возможными значениями 0 и 1, в которой
единицы занимают позиции в комбинациях кода, на которых стоят ошибочные символы.
Все остальные позиции заняты нулями. Вес вектора ошибок ei W(ei)
= ν, где ν – кратность ошибок.

Искаженная комбинация кода V*  при использовании понятия вектор ошибок
может быть представлена как результат суммы по модулю два одноименных символов
неискаженной комбинации V и вектора ошибок ei , то есть

    (7)

Поскольку в комбинации кода может
быть искажено любое число символов в пределах n и эти
символы могут занимать любые позиции в комбинации, то число ненулевых векторов
ошибок:

      (8)

где единица соответствует
нулевому вектору ошибок.

Если известен вектор ошибок, то
процедура исправления ошибок в принятой комбинации состоит в сложении по модулю
два принятой комбинации с вектором ошибок.

Действительно,

21. Методы определения разрядности блокового корректирующего
кода и нахождение его комбинаций.

Говоря ранее о разбиении
множества запрещенных комбинаций U на подмножества   Ai, мы предполагали, что комбинации кода известны,
однако практике это не так.

Известно число комбинаций,
которые должны входить в код, и подлежащие исправлению ошибки в этих
комбинациях исходя из статистики появления ошибок. При этом задача заключается
в том, чтобы найти код, который бы содержал n комбинаций и позволял исправлять известные ошибки.

Корректирующие коды «на пальцах» +54

Алгоритмы, Математика

Рекомендация: подборка платных и бесплатных курсов Java — https://katalog-kursov.ru/

Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.

Давайте же разберёмся, что это такое.

Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.

Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.

Каналы с ошибкой

Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.

Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем $k$ ошибок. Это будет характеристикой канала связи.

Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами ($A$, $B$, $C$, …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.

Кодирование и декодирование будем обозначать прямой стрелкой ($rightarrow$), а передачу по каналу связи — волнистой стрелкой ($rightsquigarrow$). Ошибки при передаче будем подчёркивать.

Например, пусть мы хотим передавать только сообщения $A=0$ и $B=1$. В простейшем случае их можно закодировать нулём и единицей (сюрприз!):

$ begin{aligned} A &to 0, B &to 1. end{aligned} $

Передача по каналу, в котором возникла ошибка будет записана так:

$ A to 0 rightsquigarrow underline{1} to B. $

Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это $0$ и $1$.

Код с утроением

Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:

$ begin{aligned} A &to 00, B &to 11. end{aligned} $

Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:

$ A to 00 rightsquigarrow 0underline{1} to ?. $

Какие выводы мы можем сделать, когда получили $01$? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква $B$. А может, во втором, и была передана $A$.

То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.

$ begin{aligned} A &to 000, B &to 111. end{aligned} $

Проверим в деле:

$ A to 000 rightsquigarrow 0underline{1}0 to A?. $

Получили $010$. Тут у нас есть две возможности: либо это $B$ и было две ошибки (в крайних цифрах), либо это $A$ и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква $A$. Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.

Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква $A$.

Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.

Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.

Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.

Расстояния между кодами

Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.

И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.

Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.

Пусть мы передавали $000$, а получили $001$. Видно, что эта цепочка больше похожа на исходные $000$, чем на $111$. А так как других кодовых слов у нас нет, то и выбор очевиден.

Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.

Можно ввести некоторую величину $d(alpha, beta)$, равную количеству различающихся цифр в соответствующих разрядах цепочек $alpha$ и $beta$. Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.

Например, $d(010, 010) = 0$, так как все цифры в соответствующих позициях равны, а вот $d(010101, 011011) = 3$.

Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:

  1. Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
  2. Расстояние в обе стороны одинаково.
  3. Путь через третью точку не короче, чем прямой путь.

Достаточно разумные требования.

Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):

  1. $d(x, y) geqslant 0,quad d(x, y) = 0 Leftrightarrow x = y;$
  2. $d(x, y) = d(y, x);$
  3. $d(x, z) + d(z, y) geqslant d(x, y)$.

Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.

Окрестности

Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.

Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.

Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.

Так, скажем, окрестность кодового слова $000$ радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:

$ {000, 100, 010, 001}. $

Да, вот так странно выглядят шары в пространстве кодов.

А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим $000$! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.

Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение $x$, мы получим один из кодов, который принадлежит окрестности $x$ радиусом 2.

Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.

Сколько ошибок может исправить код?

Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.

В коде с удвоением между кодовыми словами $00$ и $11$ расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.

Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.

Что интересно, точек касания в нашем странном пространстве у шаров две — это коды $01$ и $10$. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.

В случае кода с утроением, между шарами будет зазор.

Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).

В общем случае получаем следующее.

Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием $d_{min}$ будет успешно работать в канале с $k$ ошибками, если выполняется соотношение

$ d_{min} geqslant 2k+1. $

Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает $k$ ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса $k$ других кодовых слов. Математически это записывается так:

$d_{min}geqslant k + 1.$

Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.

$ begin{aligned} A to 10100, B to 01000, C to 00111, D to 11011. end{aligned} $

Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.

A B C D
A — 3 3 4
B 3 — 4 3
C 3 4 — 3
D 4 3 3 —

Минимальное расстояние $d_{min}=3$, а значит $3geqslant2k+1$, откуда получаем, что такой код может исправить до $k=1$ ошибок. Обнаруживает же он две ошибки.

Рассмотрим пример:

$ A to 10100 rightsquigarrow 101underline{1}0. $

Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.

$ begin{aligned} A:, d(10110, 10100) &= 1, B:, d(10110, 01000) &= 4, C:, d(10110, 00111) &= 2, D:, d(10110, 11011) &= 3. end{aligned} $

Минимальное расстояние получилось для символа $A$, значит вероятнее всего передавался именно он:

$ A to 10100 rightsquigarrow 101underline{1}0 to A?. $

Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.

Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.

Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы $2^5 = 32$ варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.

Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.

Интерлюдия: поле GF(2)

Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.

Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):

$ begin{aligned} 0 + 0 &= 0, 0 + 1 &= 1, 1 + 0 &= 1, 1 + 1 &= 0. end{aligned} $

Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.

Множество из двух элементов ${0, 1}$ с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.

У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.

$ x + x = 0. $

Это свойство прямо следует из определения.

$ x + y = x - y. $

А в этом можно убедиться, прибавив $y$ к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.

Проверяем корректность

Вернёмся к коду с утроением.

$ begin{aligned} A &to 000, B &to 111. end{aligned} $

Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.

Пусть мы приняли вектор-строку $x$ из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)

$dots rightsquigarrow x = (x_1, x_2, x_3). $

Математически равенство всех трёх цифр можно записать как систему:

$ left{ begin{aligned} x_1 &= x_2, x_2 &= x_3. end{aligned} right. $

Или, если воспользоваться свойствами сложения в GF(2), получаем

$ left{ begin{aligned} x_1 + x_2 &= 0, x_2 + x_3 &= 0. end{aligned} right. $

Или

$ left{ begin{aligned} 1cdot x_1 + 1cdot x_2 + 0cdot x_3 &= 0, 0cdot x_1 + 1cdot x_2 + 1cdot x_3 &= 0. end{aligned} right. $

В матричном виде эта система будет иметь вид

$ Hx^T = 0, $

где

$ H = begin{pmatrix} 1 & 1 & 0 0 & 1 & 1 end{pmatrix}. $

Транспонирование здесь нужно потому, что $x$ — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.

Будем называть матрицу $H$ проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.

Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.

Кодирование

Итак, у нас есть система для проверки

$ left{ begin{aligned} x_1 + x_2 &= 0, x_2 + x_3 &= 0. end{aligned} right. $

Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице $H$) найдём кодовые слова.

Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:

$ H = begin{pmatrix} 1 & 0 & 1 & 0 & 0 0 & 1 & 1 & 0 & 1 0 & 0 & 0 & 1 & 1 end{pmatrix}. $

Соответствующая система имеет вид:

$ left{ begin{aligned} x_1 + x_3 &= 0, x_2 + x_3 + x_5 &= 0, x_4 + x_5 &= 0. end{aligned} right. $

Чтобы найти кодовые слова соответствующего кода нужно её решить.

В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если $a$ и $b$ — решения системы, то для их суммы верно

$H(a+b)^T=Ha^T+Hb^T=0+0=0,$

что означает, что она тоже — решение.

Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.

Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить $x_1, x_2, x_4$.

Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.

Итак, получаем:

$ left{ begin{aligned} x_1 &= x_3, x_2 &= x_3 + x_5, x_4 &= x_5. end{aligned} right. $

Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.

$ begin{aligned} x_3=1, x_5=0:quad x_1=1, x_2=1, x_4=0 Rightarrow x^{(1)} = (1, 1, 1, 0, 0), x_3=0, x_5=1:quad x_1=0, x_2=1, x_4=1 Rightarrow x^{(2)} = (0, 1, 0, 1, 1). end{aligned} $

Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:

$ a_1 x^{(1)}+a_2 x^{(2)}, $

где $a_1, a_2$ равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно $2^2=4$ сочетания.

Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.

$ (a_1, a_2)cdot begin{pmatrix} 1 & 1 & 1 & 0 & 0 0 & 1 & 0 & 1 & 1 end{pmatrix} = aG. $

Строчки здесь — линейно независимые решения, которые мы получили. Матрица $G$ называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:

$ a to aG. $

Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)

$ begin{aligned} 00 &to 00000, 01 &to 01011, 10 &to 11100, 11 &to 10111. end{aligned} $

Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?

$ a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to Hx^T = (110)^T neq 0. $

А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!

Для кода с утроением, кстати, порождающая матрица выглядит очень просто:

$G=begin{pmatrix}1&1&1end{pmatrix}.$

Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.

Ошибка по синдрому

Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!

Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение $x$, а было отправлено кодовое слово $v$. Тогда вектор ошибки по определению

$ e = x - v. $

Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:

$ begin{aligned} v &= x + e, x &= v + e. end{aligned} $

В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.

Как мы уже говорили раньше, если мы получили сообщение $x$ с ошибкой, то $Hx^Tneq 0$. Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?

Назовём результат умножения на проверочную матрицу синдромом:

$ s(x)=Hx^T.$

И заметим следующее

$ s(x) = Hx^T = H(v+e)^T = He^T = s(e). $

Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.

Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?

А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.

Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.

$s(x)$ $x$
$000$ $underline{00000}, 11100, 01011, 10111$
$001$ $underline{00010}, 11110, 01001, 10101$
$010$ $underline{01000}, 10100, 00011, 11111$
$011$ $01010, 10110, underline{00001}, 11101$
$100$ $underline{10000}, 01100, 11011, 00111$
$101$ $underline{10010}, 01110, 11001, underline{00101}$
$110$ $11000, underline{00100}, 10011, 01111$
$111$ $11010, underline{00110}, underline{10001}, 01101$

В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.

Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.

Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.

$ a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to s(x)=Hx^T = (110)^T to e=(00100). $

Вектор ошибки равен $(00100)$, а значит ошибка в третьем разряде. Как мы и загадали.

Ура, всё работает!

Что же дальше?

Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.

Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.

Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.

Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.

Источник

Что такое величина вектора ошибки

Модуль вектора ошибки (Error Vector Magnitude, EVM) — широко применяемый показатель системного уровня, который регламентируется различными стандартами в области связи для испытаний на соответствие в таких приложениях, как беспроводные локальные сети (WLAN 802.11), мобильная связь (4G LTE, 5G) и многие другие. Кроме того, это чрезвычайно важная системная характеристика, позволяющая количественно оценить совокупное влияние всех возможных проблем в системе с помощью одного, простого для понимания параметра. В статье проанализировано, как характеристики более низкого уровня влияют на EVM, рассмотрен ряд практических примеров использования EVM для оптимизации характеристик устройства на уровне системы, показано, как добиться снижения EVM на 15 дБ по сравнению с требованиями большинства стандартов связи.

Большинство инженеров, работающих в области радиочастотных систем, оперируют такими характеристиками, как коэффициент шума, точка пересечения третьего порядка и отношение сигнал — шум. Понимание совокупного влияния этих параметров на общие рабочие характеристики системы может быть сложной задачей. Модуль вектора ошибки позволяет быстро получить представление о работе системы в целом, вместо того, чтобы оценивать несколько разных показателей.

Что такое модуль вектора ошибки?
EVM — это простой показатель для количественной оценки комбинации всех искажений сигнала в системе. Он часто определяется для устройств, использующих цифровую модуляцию, которая может быть представлена в виде графика синфазных (I) и квадратурных (Q) векторов, известного также как «диаграмма созвездия» (constellation diagram) (рис. 1a). Как правило, EVM вычисляется путем нахождения идеального местоположения созвездия для каждого принятого символа, как показано на рис. 1б. Среднеквадратичное значение всех модулей вектора ошибки между местоположениями принятых символов и их ближайшими идеальными местоположениями в созвездии определяет величину EVM устройства [1].

где: Lp — количество кадров, Nc — количество несущих, Ri, j — принятый символ, а Si, j — идеальное местоположение символа.
EVM тесно связан с частотой битовых ошибок (BER) данной системы. Когда принятые символы располагаются далеко от целевой точки созвездия, вероятность их попадания в границу принятия решения другой точки созвездия увеличивается. Это приводит к увеличению BER. Важное различие между BER и EVM состоит в том, что BER для переданного сигнала вычисляется на основе переданной битовой комбинации, в то время как EVM вычисляется на основе расстояния от ближайшей точки созвездия символов до местоположения символа. В некоторых случаях символы могут пересекать границу принятия решения, и им присваивается неправильная битовая комбинация. Если символ попадает ближе к другому идеальному местоположению символа, это может улучшить EVM для этого символа. Таким образом, хотя EVM и BER тесно связаны, эта связь может быть нарушена при очень высоких уровнях искажения сигнала.
Современные стандарты в области связи устанавливают минимально допустимый уровень EVM на основе характеристик передаваемого или принятого сигнала, таких как скорость передачи данных и полоса пропускания. Устройства, которые достигают целевого уровня EVM, соответствуют стандарту, в то время как устройства, которые не достигают целевого уровня EVM, не соответствуют его требованиям. Испытательное и измерительное оборудование, предназначенное для проверки на соответствие стандартам, обычно ориентировано на более строгие целевые значения EVM, которые могут быть на порядок ниже требуемых в стандарте. Это позволяет оборудованию определять EVM тестируемого устройства без значительных искажений сигнала.

Что влияет на EVM?
Как показатель ошибки, EVM тесно связан со всеми источниками искажений в системе. Мы можем количественно оценить влияние всех отклонений в системе на EVM, вычислив, как они искажают принимаемые и передаваемые сигналы. Проанализируем влияние нескольких ключевых видов помех, таких как тепловой шум, фазовый шум и нелинейности, на EVM.

Белый шум
Белый шум присутствует во всех радиочастотных системах. Когда шум является единственным искажением в системе, результирующий EVM можно рассчитать по следующей формуле:

где NSD — спектральная плотность шума в дБ ПШ / Гц, BW — ширина полосы сигнала в Гц, PAPR — отношение пиковой мощности к средней, а Pbackoff — разница между пиковой мощностью сигнала и полным диапазоном измерений преобразователя.
Эта формула может быть очень удобна для прямого расчета ожидаемого значения EVM устройства с использованием значения NSD, которое обычно указывается для современных высокоскоростных преобразователей. Обратите внимание, что для высокоскоростных преобразователей необходимо учитывать также шум квантования. Величина NSD большинства высокоскоростных преобразователей также включает шум квантования. Следовательно, для этих устройств уравнение 3 отражает не только тепловой шум, но также шум квантования.
Как показывают эти два уравнения, EVM сигнала напрямую зависит от общей полосы пропускания сигнала, отношения пиковой мощности к средней и теплового шума системы.

Как фазовый шум влияет на EVM
Другим видом шума, который влияет на EVM системы, является фазовый шум, который представляет собой случайные флуктуации фазы и частоты сигнала [3]. Все нелинейные элементы схемы вносят фазовый шум. Основные источники фазового шума в данной системе могут быть прослежены вплоть до генераторов. Генератор частоты дискретизации преобразователя данных, используемый для преобразования частоты гетеродин и генератор опорной частоты — все эти устройства могут вносить вклад в общий фазовый шум системы.
Ухудшение характеристик из-за фазового шума зависит от частоты. Для типичного генератора большая часть энергии несущей приходится на его основную частоту генерации, которая называется центральной частотой. Часть энергии сигнала будет распределяться около этой центральной частоты. Отношение амплитуды сигнала в полосе частот 1 Гц при определенном сдвиге частоты к его амплитуде на центральной частоте определяется как фазовый шум при этом конкретном частотном сдвиге, как показано на рис. 2.

Описание критериев оценки качества сигналов

В этой главе будет рассказывается о существующих критериях оценки качества модулированных сигналов. Будет сделан выбор в пользу одного из них.

Частота ошибочных бит

BER (Bit Error Ratio), или Коэффициент битовых ошибок. Он характеризует частоту появления ошибочно восстановленных битов в демодулированном потоке данных. Он равен отношению числа ошибочных битов к общему числу битов, переданных за время проведения теста.

Коэффициент ошибок модуляции

MER (Modulation Error Ratio) — это ошибка модуляции, характеризующая, отклонение реального символа от местоположения символа идеального на векторной диаграмме. Величина MER соответствует размеру кластера (скопления) вокруг заданных точек на точечной диаграмме (рис. 1.1). Большое значение MER будет указывать на меньший размер кластеров.

Рис. 1.1 Точечная диаграмма для 64 QAM

Модуль вектора ошибок(EVM)

В процессе модуляции могут изменяться как амплитуда, так и фаза/частота колебаний. Максимальный объём передаваемой информации достигается при одновременном изменении амплитуды и фазы сигнала. Однако сгенерировать или декодировать такой сигнал непосредственно (с помощью амплитудного и фазового модуляторов) тяжело. На практике данное решение осуществляют и описывают с помощью квадратурных модуляторов и полярных координат, образованных парой ортогональных векторов напряжений: синфазного с несущим колебанием I и сдвинутого на 90° Q. Такое представление позволяет рассматривать любую точку в полярных координатах в виде набора координат напряжений (I, Q) либо в виде вектора, определяемого амплитудой и фазой (рис. 1.2). Соответственно, реализованная и описанная таким образом модуляция называется векторной, а полярные координаты — диаграммой состояний.

При этом погрешность векторной модуляции определяется отличием реальной траектории или положения точки, соответствующей заданной модуляции, от идеальной.

Для цифровой векторной модуляции наиболее распространённой величиной, описывающей погрешность модуляции, является модуль вектора ошибки EVM.

Рис.1.2 Диаграмма состояний векторной модуляции

На рисунке 1.3 изображена векторная диаграмма, на которой показаны два вектора — опорный вектор, s(k), и реальный измеренный вектор, z(k), который соответствует принятого символа. Опорный вектор определяет координаты идеальной траектории символа при отсутствии ошибок. Разность между опорным вектором и вектором реально измеренного символа называется вектором ошибки, e(k).

Модуль вектора ошибки(EVM, error vector magnitude) представляет собой евклидово расстояние между координатами идеального и реально измеренного символов. В общем случае, EVM усредняется по ансамблю траекторий символов и описывается следующим выражением.

Таким образом, параметр EVM является мерой отношения вектора ошибки к опорному вектору. В совершенной системе, в которой отсутствуют шумы и нелинейности, способные внести искажения в сигнал, измеренный и опорный векторы совпадали бы, и EVM был бы равен нулю.

Рис. 1.3. Иллюстрация сигнала ошибки с помощью векторной диаграммы

Оптимизация приемника при помощи анализа модуля вектора ошибки

Теоретические основы анализа модуля вектора ошибки

На рис. 1 изображена векторная диаграмма, на которой показаны два вектора — опорный вектор, R (k), и реальный измеренный вектор, Z (k), который соответствует траектории принятого символа. Опорный вектор определяет координаты идеальной траектории символа при отсутствии ошибок. Разность между опорным вектором и вектором реально измеренного символа называется вектором ошибки.

Модуль вектора ошибки (EVM, error vector magnitude) представляет собой евклидово расстояние между координатами идеального и реально измеренного символов. В общем случае, EVM усредняется по ансамблю траекторий символов и описывается следующим выражением:

Таким образом, параметр EVM является мерой отношения вектора ошибки к опорному вектору. В совершенной системе, в которой отсутствуют шумы и нелинейности, способные внести искажения в сигнал, измеренный и опорный векторы совпадали бы, и EVM был бы равен нулю. Рассмотрим влияние отношения «сигнал — шум» (ОСШ) для принимаемого символа. При очень большом ОСШ разница между измеренным и опорным векторами, обусловленная шумом и искажениями, очень мала, а EVM стремится к нулю. И, наоборот, большое значение EVM подразумевает, что вектор измеренного символа значительно отличается от идеального опорного вектора, что может быть вызвано только шумом и искажениями (при условии, что при задании опорного вектора не была допущена ошибка). Таким образом, ОСШ и EVM модулированного сигнала связаны друг с другом обратной зависимостью, которая описывается уравнением:

где L — это выигрыш за счет кодирования.

Параметр L учитывает выигрыш, который достигается за счет схемы кодирования сигнала. Информативное сообщение может кодироваться различными способами. Например, в системах с расширением спектра прямой последовательностью информационное сообщение подвергается расширению спектра путем умножения каждого передаваемого бита на прямую (псевдослучайную) последовательность, представляющую собой случайную последовательность нулей и единиц. Последовательность подбирается таким образом, чтобы она была уникальной и слабо коррелированной с последовательностями, которые применяются для кодирования других потоков, передаваемых на той же частоте несущей. Для систем с расширением спектра усиление за счет кодирования равно количеству элементов, или «чипов», в последовательности, используемой для кодирования каждого бита. В децибелах эта величина выражается как 10log10 (частота следования элементов последовательности / скорость данных). Например, для передачи потока данных со скоростью 12,2 кбит/с в трансивере стандарта UMTS используется последовательность со скоростью 3,84 Мчип/с; при этом выигрыш за счет кодирования равен 3,84×10 6 /12,2×10 3 = 314,75, или 25 дБ.

Для нахождения зависимости между EVM и BER необходимо определить, как связаны друг с другом ОСШ и вероятность ошибки на символ для конкретной схемы модуляции. Вероятность ошибки на символ для сигналов с квадратурной амплитудной модуляцией (QAM) описывается выражением (3):

где M — порядок модуляции (например, 64 для 64-QAM), γb — среднее значение ОСШ на бит, k — число битов на символ (например, 6 битов на комплексный символ для 64-QAM).

Используя выражения (2) и (3), можно построить зависимости частоты ошибки на символ (SER, symbol error rate) и EVM от ОСШ. Зависимость SER от ОСШ показана на рис. 2а. Для форматов QAM с различным порядком она имеет классический вид типа «водопад». Для тех же схем модуляции на рис. 2б изображены зависимости EVM от ОСШ. С помощью этих зависимостей разработчики могут оценить значение частоты ошибок на бит для конкретного приемника. Например, если измеренное значение EVM для некодированного сигнала с модуляцией 256-QAM равно 3%, то ожидаемая частота ошибок на символ составит 600 млн –1 . Другими словами, в последовательности из 10 000 символов в среднем 6 символов будут ошибочными, что соответствует 75 ошибочным битам в последовательности из 1 миллиона битов (BER = 7,5×10 -5 ).

Используя зависимости, показанные на рис. 2, а также подходящий векторный анализатор сигналов, разработчик может достаточно быстро оптимизировать производительность системы. Это достигается путем контроля значения EVM при изменении таких характеристик сигнального тракта, как тип фильтра, межкаскадное согласование и усиление преобразования. Рис. 3 иллюстрирует некоторые распространенные искажения сигнальных созвездий, которые могут возникать в реальной системе. На основании формы сигнального созвездия можно сделать определенные выводы о природе шумов или искажений, являющихся потенциальной причиной ухудшения EVM.

Пример оптимизации: подсистема трактов ПЧ и модулирующих частот AD8348/AD8362

На рис. 4 показана приемная подсистема для переноса сигнала из области ПЧ в область модулирующих частот с замкнутым контуром автоматической регулировки уровня (automatic level control — ALC), основанная на квадратурном демодуляторе и детекторе среднеквадратической мощности. Микросхема AD8348 обеспечивает точную квадратурную демодуляцию сигналов с частотой от 50 МГц до 1 ГГц. Внутренний делитель частоты гетеродина позволяет работать с частотой гетеродина, равной удвоенной частоте несущей, что облегчает решение проблемы, связанной с паразитным захватом частоты гетеродина (LO-pulling) в полнодуплексных трансиверах. В рассматриваемом примере входной сигнал имеет частоту (ПЧ), равную 190 МГц, а сигнал гетеродина имеет уровень, равный 10 дБм, и частоту, равную 380 МГц. Интегрированный входной усилитель с переменным коэффициентом усиления (variable gain amplifier — VGA), состоящий из резистивного переменного аттенюатора и пост-усилителя с высоким значением IP, обеспечивает переменный коэффициент усиления при сохранении постоянного динамического диапазона, свободного от побочных составляющих. Микросхема AD8362 — это прецизионный измеритель мощности, способный измерять среднеквадратическое значение мощности сигналов в диапазоне от произвольных низких частот до 2,7 ГГц. Данная микросхема не чувствительна к изменению пик-фактора сигнала, что делает ее подходящим решением для измерения истинной среднеквадратической мощности сигналов с цифровой модуляцией.

В схеме на рис. 4 обеспечивается измерение среднеквадратической мощности сигнала в полосе модулирующих частот, поступающего с синфазного канала. Выбор синфазного или квадратурного канала для детектирования произволен, если вектора I и Q имеют псевдослучайный характер, что соответствует истине для большинства схем цифровой модуляции. На основании результата измерения среднеквадратической мощности интегрированный усилитель ошибки формирует управляющий сигнал, подаваемый на вход управления усилением квадратурного демодулятора. Замкнутый контур регулировки адаптивно подстраивает усиление преобразования демодулятора для поддержания постоянного среднеквадратического уровня мощности модулирующего сигнала независимо от его формы. Выходной уровень задается подачей соответствующего напряжения контрольной точки на вывод VSET. Для нахождения оптимальной контрольной точки в схеме ALC и определения подходящего фильтра для цифровой модуляции 256-QAM со скоростью 1 Мсимвол/с использовался метод анализа вектора ошибки.

Несимметричные сигналы с выхода демодулятора подаются на фильтр нижних частот. Для минимизации широкополосного шума и подавления мешающих смежных каналов приема в обоих каналах, I и Q, использовались фильтры Бесселя четвертого порядка. Выбор в пользу фильтра Бесселя обусловлен его малой групповой задержкой, что является необходимым требованием для минимизации межсимвольных помех. На этапе тестирования сначала использовались фильтры Баттерворта и Чебышева, но из-за большей групповой задержки в полосе пропускания значения EVM в системе были хуже. С помощью анализатора сигналов можно очень быстро измерить показатели системы, что позволяет подобрать оптимальную схему фильтра за короткий промежуток времени.

Для измерения EVM в полосе модулирующих частот использовался векторный анализатор сигналов FSQ8 производства Rohde&Schwarz. Оптимальное значение напряжения контрольной точки было найдено путем изменения этого напряжения и наблюдения соответствующего значения EVM. Как показано на рис. 5, при правильном выборе контрольной точки EVM составляет не более 2% в диапазоне входных уровней, превышающем 40 дБ. На рис. 6 показано экспериментально полученное сигнальное созвездие для модуляции 256-QAM. Переменное усиление преобразования демодулятора позволяет создавать схемы, обладающие оптимальными характеристиками BER в более широком динамическом диапазоне, чем при использовании модуляторов с фиксированным коэффициентом усиления.

Рис. 7 иллюстрирует показатели EVM для модуляции QAM меньших порядков при той же ширине полосы сигнала. Для достижения адекватных значений BER при использовании схем модуляции более низкого порядка требуется меньшее ОСШ. Поэтому неудивительно, что для таких схем модуляции показатели EVM еще лучше, а динамический диапазон — немного больше.

Значение EVM можно оценить по напряжению RSSI (Received Signal Strength Indication, индикация уровня принимаемого сигнала) микросхемы AD8362. На рис. 8 показаны результаты измерений напряжения RSSI для нескольких схем модуляции. Зная напряжение RSSI, можно определить уровень мощности сигнала на входе демодулятора с приемлемой погрешностью, который затем может быть использован для предсказания значения EVM при этом уровне входной мощности.

Заключение

Измерение EVM и связанных с ним величин позволяет оценить качество цифрового радиоприемника. Кроме того, при правильном применении методы анализа EVM позволяют идентифицировать вид искажений сигнала и, следовательно, конкретное место возникновения ошибок. Таким образом, анализ EVM представляет собой удобный инструмент для оптимизации сигнального тракта и предсказания динамических характеристик системы.

источники:

http://vuzlit.ru/2225102/opisanie_kriteriev_otsenki_kachestva_signalov

Оптимизация приемника при помощи анализа модуля вектора ошибки

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите эти материалы по теме:

  • Яндекс еда ошибка привязки карты
  • Вертикальная стиральная машина электролюкс выдает ошибку
  • Верстка печатного издания основные ошибки верстки
  • Вероятность ошибки второго рода это
  • Вероятность ошибки второго рода формула

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии