Нормально распределенные непрерывные случайные величины.
Вентцель Е. С. Гл.
6.
Гмурман В. Е. Гл.
12.
Роднищев Н.Е. Гл.4.
Среди распределений
непрерывных случайных величин центральное
место занимает нормальный закон
распределения (закон Гаусса). Этот закон
распределения наиболее широко
распространен в тех случаях, когда
случайная величина является ре зультатом
действия большого числа различных
факторов, причем каждый фактор в
отдельности на случайную величину
влияет незначительно. Так случайными
величинами, имеющими нормальное
распределение, могут быть: отклонение
действительных размеров деталей,
выпускаемых станком-автоматом, ошибки
измерения и т.п. Основная особенность
нормального распределения, которая
выделяет его из других распределений,
заключается в том, что оно является
предельным законом распределения, к
которому приближаются другие распределения.
В дальнейшем будет рассмотрена так
называемая центральная предельная
теорема теории вероятностей, в которой
доказывается, что при достаточно большом
числе независимых случайных величин,
подчиненных некоторым законам
распределения, их сумма будет иметь
закон распределения сколь угодно близкий
к нормальному.
При изучении этого
раздела обратить внимание на ряд формул,
имеющих большое практическое значение:
на формулу для вероятности попадания
нормально распределенной случайной
величины на заданный интервал, на формулу
для вероятности отклонения случайной
величины от своего математического
ожидания, по абсолютной величине не
превышающего заданного значения.
Вопросы для
самопроверки: Роднищев Н.Е. стр. 70.
Вопросы для
самопроверки.
-
Какое распределение
непрерывной случайной величины
называется нормальным распределением? -
Изобразить график
плотности распределения вероятности
нормального распределения и пояснить:
как будет изменяться форма этого графика
при изменении математического ожидания
и среднего квадратичного отклонения? -
Написать и пояснить
формулу для определения вероятности
попадания нормально распределенной
случайной величины в заданный интервал.
Что называется функцией Лапласа или
интегралом вероятности, и каковы ее
свойства? -
Записать формулу
для вероятности отклонения нормльно
распределенной случайной величины от
своего математического ожидания, по
абсолютной величине не превышающего
заданного значения. -
В чем заключается
правило «трех сигм»? -
Чем объясняется
широкое распространение на практике
нормального распределения?
Примеры решения
задач к части
2.Случайные величины
Задача 1. Испытывается
устройство, состоящее из двух независимо
работающих приборов. Вероятности отказа
приборов таковы: 0,2; 0,1. Найти математическое
ожидание и дисперсию случайного числа
отказавших приборов.
Решение. Случайная
величина Х – число отказавших приборов
– в данной задаче может принимать
случайно значения: 0, 1, 2 соответствующими
веро ятностями. Определим эти вероятности.
Значение
,
равное нулю, соответствует случаю, когда
не откажет ни первый, ни второй прибор.
Очевидно,.
Значение,
равное 1, отвечает случаю, когда первый
прибор откажет, а второй нет, или второй
прибор откажет, а первый нет. В этом
случае.
Наконец, значение,
равное 2, соответствует случаю, когда
откажут оба прибора совместно. Естественно,
что.
Легко убедится, что.
Математическое
ожидание случайной дискретной величины
определяется по формуле
.
Для вычисления
дисперсии удобно воспользоваться
формулой
.
В результате вычислений получим
.
Задача 2. Изделия
независимо испытываются на надежность.
вероятность для каждого изделия выйти
из строя p.
Испытания
заканчиваются после первого же изделия,
не выдержавшего испытания. Найти формулу
для ряда распределения, определить
математическое ожидание случайного
числа испытаний.
Решение. Отметим,
что в данной задаче испытания заканчиваются
на i-м
изделии (i=1,2,3,…),
если первые i-1
изделия пройдут испытания, а i-е
выйдет из строя.
Обозначим
— случайное число испытаний. Очевидно,
что для ряда распределения можно записать
следующую аналитическую формулу
особенностью
данной задачи является то, что i
– число
испытаний — представляет бесконечное
счетное множество значений, причем
вероятность
при неограниченном ростеi
стремится к нулю. В силу свойства ряда
распределения сумма всех вероятностей
должна равняться единице, т.е.
.
Убедимся в этом.
Ряд
представляет собой бесконечную убывающую
геометрическую прогрессию со знаменателем
1-p
и поэтому
.
Следовательно,.
В соответствии с
общей формулой, математическое ожидание
дискретной случайной величины Х
запишется следующим образом
Вычислим ряд
.
Для удобства введем величинуq
= 1-p.
Тогда последний ряд запишется в виде,
для вычисления которого воспользуемся
следующим приемом.
Рассмотрим ряд,
представляющий бесконечную убывающую
геометрическую прогрессию:
.
Продифференцировав последнее поq,
будем иметь
.
Левая часть этого равенства представляет
ряд.
Возвращаясь к величинеp,
можем записать
.
Таким образом,.
Задача 3. Цилиндрические
валики, изготовляемые автоматом,
считаются стандартными, если отклонение
диаметра валика от проектного размера
не превышает 3 мкм. Случайные отклонения
диаметра валика от проектного подчиняются
нормальному распределению с параметрами
m
= 0, σ
= 1,6 мкм. Сколько процентов стандартных
валиков будет изготовлять автомат?
Решение. Обозначим
через Х
– случайные отклонения диаметра валика
от проектного размера. Равенство
математического ожидания нулю (m
= 0) означает, что случайные отклонения
будут группироваться около проектного
размера (систематическая ошибка
отклонения отсутствует).
Для определения
вероятности события
мкм воспользуемся формулой теории
вероятностей
где

– допустимое отклонение по абсолютной
величине Х
от своего математического ожидания (в
данной задаче δ
= 2 мкм, т
= 0), σ
– среднее квадратичное отклонение Х.
Искомая вероятность
Р(|Х|
< 2 мкм) = 2Ф(2/1,6) = 2Ф(1,25). По таблице функции
Лапласа находим Р(|Х|
< 2) = 0,789 = 78,9%.
Задача 4. Высотомер
самолета имеет случайную и систематическую
ошибки. Систематическая ошибка равна
20м. Случайная ошибка распределена
нормально. Какое среднее квадратичное
отклонение должна иметь случайная
ошибка высотомера, чтобы с вероятностью
0.9 ошибка измерения высоты была меньше
100м.
Решение. Обозначим
Нист
— истинная
высота полета самолета, Н
– случайная величина – показание
высотомера. По условию задачи задано,
что вероятность события
Нист-100<Н<Нист+100
равна 0,9.
Для решения задачи
воспользуемся формулой теории вероятностей
для вероятности попадания случайной
величины в заданный интервал
,
где Ф(t), как и в
предыдущей задаче, функция Лапласа. В
данной задаче a=Hист-100
м, b=
Hист+100
м. В результате можно записать
.
Систематическая
ошибка представляет собой неслучайную
величину mH
— Hист,
которая по условию задачи равна 20м. С
учетом этого приходи к следующему
уравнению относительно Н
:
.
Учитывая, что
функция Лапласа – нечетная функция
(Ф(-t)=-Ф(t)),
окончательно запишем 0,9=Ф(80/Н)+Ф(120/Н).
Последнее уравнение является
трансцендентным, решение которого можно
найти приближенно путем проб: Н58
м.
Задачи к части
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сообщения без ответов | Активные темы | Избранное
|
|
Задача на параметр сигма в нормальном распределении
|
|
29/11/16 |
Здравствуйте, Пытаюсь решить задачу из учебника по теории вероятностей МГТУ им. Баумана (задача 4.39). Вот условие задачи. Высотомер имеет случайную и систематическую погрешности. Систематическая погрешность равна 20 м. Случайная погрешность распределена по нормальному закону. Какую среднюю квадратичную погрешность должен иметь прибор, чтобы с вероятностью 0.9452 погрешность измерения высоты была меньше 10 м? Если я правильно понимаю, то систематическая погрешность не имеет отношения к распределению случайной погрешности, т. е. параметр где Буду очень благодарен, если кто-то сможет сориентировать меня в нужном направлении.
|
|
|
|
|
Brukvalub |
Re: Задача на параметр сигма в нормальном распределении
|
||
01/03/06 |
параметр Первое не согласуется со вторым.
|
||
|
|
|||
|
JSBach |
Re: Задача на параметр сигма в нормальном распределении
|
|
29/11/16 |
|
|
|
|
|
AV_77 |
Re: Задача на параметр сигма в нормальном распределении
|
||
11/11/07 |
Систематическая погрешность фиксирована — если намеряли
|
||
|
|
|||
|
JSBach |
Re: Задача на параметр сигма в нормальном распределении
|
|
29/11/16 |
Систематическая погрешность фиксирована — если намеряли Я так и думал. Правда, остается сомнение относительно понимания термина «случайная погрешность». Я так понял, что это «добавочная» погрешность — которая приплюсовывается к систематической. Т. е. общая погрешность измерения равна Если же под случайной погрешностью следует понимать общую погрешность, то что тогда выходит… Нужно ли тогда принять Где же собака зарыта?…
|
|
|
|
|
ewert |
Re: Задача на параметр сигма в нормальном распределении
|
||
11/05/08 |
К этому надо просто привыкнуть. Систематическая погрешность — это матожидание (т.е. погрешность калибровки прибора), случайная — это сигма (дополнительная погрешность за счёт неизвоиспроизводимости измерений из-за неизвестности того, какая утка и когда и на какое крыло ляжет). Ну это просто такой физический жаргон.
|
||
|
|
|||
|
JSBach |
Re: Задача на параметр сигма в нормальном распределении
|
|
29/11/16 |
|
|
|
|
|
JSBach |
Re: Задача на параметр сигма в нормальном распределении
|
|
29/11/16 |
После некоторого перерыва решил вернуться к этому учебнику и опять наткнулся на трудности с данной задачей. Поиск в интернете дал ссылку на ресурс с решением практически такой же задачи (только значения в условии немного отличаются). https://studfiles.net/preview/2015038/page:6/ Прочитав и проанализировав решение на указанном ресурсе, пришел к выводу, что мои рассуждения были все-таки верными в целом. Были некоторые нюансы, но все равно в конечном итоги все приходит к вычислению выражения Из этого выражения очевидно, что искомая вероятность не может быть больше К сожалению, из этого приходится сделать вывод, что никто из ответивших, по всей видимости, не удосужился попытаться решить задачу. То, что данные в условии не сходятся, стало бы очевидным для специалиста, попытавшегося эту задачу решить, и следовало бы указать в первую очередь именно на это (я на месте помогающего так и сделал бы). Кроме того, несколько удивило то, что искомое значение действительно (как я и предполагал) приходится искать подбором. Видимо, это характерно для некоторых задач из некоторых разделов математики — теории вероятностей в частности.
|
|
|
|
|
Евгений Машеров |
Re: Задача на параметр сигма в нормальном распределении
|
||
11/03/08 |
При измерениях систематическую погрешность (определённую при поверке и занесённую в паспорт прибора) вычитают. То есть учитывать её в данной задаче вообще не надо. Для чего она приведена — возможно, имитируется реальный расчёт, при котором она задана, и расчётчик должен понимать, какие данные нужны для расчёта, а какие нет.
|
||
|
|
|||
|
Someone |
Re: Задача на параметр сигма в нормальном распределении
|
||
23/07/05 |
Перебор — один из способов решения, но не лучший. Вообще-то надо применить какой-то способ решения нелинейных уравнений, например, Ньютона. Но в частном случае может хватить и перебора. А в данном случае наверняка нужно воспользоваться таблицей значений функции
|
||
|
|
|||
|
novichok2018 |
Re: Задача на параметр сигма в нормальном распределении
|
||
16/04/18 |
Ф — нечётная? Можно упростить уравнение?
|
||
|
|
|||
|
Евгений Машеров |
Re: Задача на параметр сигма в нормальном распределении
|
||
11/03/08 |
Она не нечётная, но может быть представлена суммой константы и нечётной функции. Так что для данных значений аргумента расчёт, как тут подсказывают, сведётся к заглядыванию в имеющуюся в большинстве учебников таблицу.
|
||
|
|
|||
|
Someone |
Re: Задача на параметр сигма в нормальном распределении
|
||
23/07/05 |
Судя по некоторым косвенным признакам, у топикстартера нечётная:
|
||
|
|
|||
|
Евгений Машеров |
Re: Задача на параметр сигма в нормальном распределении
|
||
11/03/08 |
Такая — нечётная. Я о функции распределения, которая в минус бесконечности ноль, в плюс бесконечности один.
|
||
|
|
|||
|
JSBach |
Re: Задача на параметр сигма в нормальном распределении
|
|
29/11/16 |
То есть учитывать её в данной задаче вообще не надо. Не согласен. Такой вариант я уже пробовал еще при первом подходе к решению задачи. Если подставить в формулу Судя по некоторым косвенным признакам, у топикстартера нечётная: Совершенно верно.
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: Xo4y3HaTb |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,667 -
гуманитарные
33,655 -
юридические
17,917 -
школьный раздел
612,004 -
разное
16,907
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Его решение имеет вид ш Ьг аг 2(1пЬ вЂ” 1па) 158 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Нетрудно проверить, что при фиксированных значениях а и Ь, в силу условия О < а < Ь < +со справедливы соотношения Р(а < Х < Ь) = Фо( ) Фо(-) — +О Ь а Р1а <Х <Ь) =Фо( — ) Фо( ) — + О. Позтому вероятность Р(а < Х < Ь) при (Ь2 2) 2(1п Ь вЂ” 1па) принимает максимальное значение. Вопросы и задачи 4.1. Дайте определение случайной величины. 4.2. Что называют законом распределения (вероятностей) случайной величины? 4.3.
Дайте определение функции распределения (вероятностей). Перечислите и докажите свойства функции распределе- 4.4. Как, зная функцию распределения, найти вероятность попадания случайной величины в заданный интервал? 4.5. Какие свойства должна иметь некоторая функция для того, чтобы она могла быть функцией распределения? 4.6. Какую случайную величину называют дискретной? Приведите примеры дискретных случайных величин.
4.7. Что называют рядом распределения дискретной случайной величины? Как еще можно задать закон распределения дискретной случайной величины? Волросм иэалачя 159 4.8. Какой вид имеет функция распределения дискретной случайной величины? 4.9. Какое распределение называют биномиальным? 4.10. Какое распределение называют распределением Пуассона? 4.11.
Какое распределение называют геометрическим распределением? 4.12. Какую случайную величину называют непрерывной? Приведите примеры непрерывный случайных величин. 4.13. Дайте определение плотности распределения (вероятностей). Перечислите и докажите свойства плотности распределения. Существует ли плотность распределения у дискретной случайной величины? 4.14. Как, зная плотность распределения, найти вероятность попадания случайной величины в заданный интервал? 4.15. Чем различаются графики функций распределения дискретной и непрерывной случайных величин? 4.18. Какое распределение называют равномерным? 4.17.
Какое распределение называют экспоненциальным (показательным)? 4.18. Какое распределение называют нормальным? 4.19. Как выглядит график плотности нормального распределения? 4.20. Что называют интегралом Лапласа? Как, пользуясь таблицей значений интеграла Лапласа, вычислить вероятность попадания нормально распределенной случайной величины в некоторый интервал? 4.21. Какое распределение называют распределением Вейбулла? 160 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 4.22.
Какое распределение называют гамма-распределением? 4.23. Из партии в 10 деталей, среди которых две бракованные, наудачу выбирают три детали. Найдите закон распределения числа бракованных деталей среди выбранных. Постройте функцию распределения. Ответ: 4.24. Вероятность приема самолетом радиосигнала при каждой передаче равна 0,7. Найдите ряд распределения и функцию распределения числа Х принятых сигналов при шестикратной передаче. Ответ: Ряд распределения и функцию распределения случайной величины Х легко построить, зная, что Р(Х = з) = =Со1(0,7)'(0,3)о ‘, 4 =0,6. 4.25.
Найдите закон распределения случайной величины Х вЂ” числа таких бросаний трех игральных костей, в каждом из которых ровно на двух костях появится по 2 очка, если общее число бросаний равно 15. Ответ: Р(Х=з)=С11зр’Чы ‘, 4=0,15, где р=Сз(1/6)~(5/6) = = 5/72 я~ 0,0694. 4.26. В течение часа на станцию скорой помощи поступает случайное число Х вызовов, распределенное по закону Пуассона с параметром Л = 5. Найдите вероятность того, что в течение часа поступит: а) ровно два вызова; б) не более двух вызовов; в) не менее двух вызовов. О, С.Сз-с 7/15 Р(Х з) зз 4=0,1,2; Р(х) = С1зо 14/15 1, х<0; х Е (О, 1]; х Е (1, 2]; х > 2.
161 Вопросы и задачи Ответ: а) Р1Х =2) =5эе ~/2! 0,086; б) Р(Х < 2) = (5о/О! + 51/1! + 5э/2!)е а — 0,127; в) Р1Х ) 2) = 1 — Р1Х < 2) = 1 — (5е/О!+ 51/1!)е ~ 0,041. 4.27. Число вызовов, поступающих на АТС (автоматическая телефонная ставция) каждую минуту, распределено по закону Пуассона с параметром Л = 1,5. Найдите вероятность того, что за минуту поступит: а) ровно три вызова; б) хотя бы один вызов; в) менее пяти вызовов. Ответ: а) 0,12551; б) 0,77687; в) 0,98143.
4.28. В приборный отсек космического корабля за время полета попадает случайное число частиц, распределенное по закону Пуассона с параметром Л, причем вероятность попасть в блок управления, расположенный в отсеке космического корабля, для каждой иэ этих частиц равна р. Определите вероятность попадания в блок: а) ровно й частиц; б) хотя бы одной частицы. Ответ: а) (Лр)»е «и/й!; 6) 1 — е ~’з. 4.29. По цели производят серию независимых выстрелов до первого попадания.
Даны вероятность р попадания в цель при одном выстреле и запас патронов и. Найдите ряд распределения и функцию распределения числа Х израсходованньп~ патронов. рд’ ‘, з’=б;и:Т (9=1-р); Ответ: Р1Х =з) = ! 9 ~ Ф=п. 4.30. Летательный аппарат, по которому ведется стрельба, состоит из двух различных по уязвимости частей. Аппарат выходит из строя при одном попадании в первую часть или трех попаданиях во вторую.
Стрельба ведется до поражения летательного аппарата. Постройте ряд распределения и функцию 6 — той 162 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ распределения числа попаданий Х в летательный аппарат, которое понадобится для его поражения, если каждый попаюпий в аппарат снаряд с вероятностью 0,3 поражает первую часть и с вероятностью 0,7 — вторую. О т в е т: Р(Х = 1) = 0,3; Р [Х = 21 = 0,21; Р(Х = 3) = 0,49.
4.31. Непрерывная случайная величина Х распределена по экспоненцизльному закону с параметром А = 0,2. Найдите вероятность попадания этой случайной величины в интервал (О, 2). Ответ: 1 — е е4 я~ 0 33. 4.32. Длительность времени Х безотказной работы элемента имеет экспоненцизльное распределение с параметром Л = = 0,02 ч 1. Вычислите вероятность того, что за время $ = 100 ч элемент: а) выйдет из строя; б) будет исправно работать. Ответ: а) 1 — е з ж0,865; б) е з 0,135. 4.33. Случайная величина Х имеет нормальное распределение с параметрами гп = 2 и и = 1. Определите вероятность попадания случайной величины в интервал (1, 5).
Ответ: 0,83999. 4.34. Случайная величина Х распределена по нормальному закону с параметрами т = 4 и и = 1. Определите вероятность попадания случайной величины Х в интервал (6, 8). Ответ: 0,0227. 4.35. Случайная величина Х имеет нормальное распределение с параметрами т и и. Вычислите вероятность попадания случайной величины в интервал (пз — 4о’, т). Ответ: 0,499971. 4.36.
Случайная величина Х подчинена нормальному закону распределения с тп = О. Вероятность попадания случайной величины в интервал (-0,3, 0,3) равна 0,5. Найдите среднее квадратичное отклонение и. Ответ: о 0,44. 153 Воиросьг и задачи 4.3Т. Измерительный прибор имеет систематическую погрешность 5 м. Случайные погрепности подчиняются нормальному закону со средним квадратическим отклонением, равным 10 м. Какова вероятность того, что погрешность измерения не превзойдет по абсолютному значению 5 м? Ответ: 0,3413.
4.38. Измерение дальности до объекта сопровождается случайными погрешностями, подчиняющимися нормальному закону со средним квадратичным отклонением, равным 50 м. Систематическая погрешность отсутствует. Найдите: а) вероятность измерения дальности с погрешностью, не превосходящей по абсолютному значению 100 м; б) вероятность того, что измеренная дальность не превзойдет истинной. Ответ: а) 0,9545; б) 0,5. 4.39.
Высотомер имеет случайную и систематическую погрешности. Систематическы погрешность равна 20 м. Случайная погрешность распределена по нормальному закону. Какую среднюю квадратичную погрешность должен иметь прибор, чтобы с вероятностью 0,9452 погр~пность измерения высоты бь|ла меньше 10 му Ответ: 50 м. 4.40. Случайны величина Х распределена по нормальному закону с математическим ожиданием пз и средним квадратичным отклонением о. Определите абсциссы и ординаты точек перегиба кривой плотности распределения. Ответ: шло; е 1~з/(а~(2~г). 4.41. Нормально распределенная случайная величина Х имеет математическое ожидание, равное нулю.
Найдите среднее квадратичное отклонение а,при котором вероятность попадания случайной величины в интервал (5, 10) была бы наибольшей. О: = ~/75Д2) 2). 164 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 4.42. Время Х (в часах) безотказной работы электрической лампочки имеет распределение Вейбулла с параматрами а = = 0,02 и ~3 = 0,5. Определите вероятность того, что лампочка проработает не менее 10000 ч. Ответ: Р(Х ) 100001 =е ~Ли~сесе -0,14. 4.43. Время Х (в месяцах) безотказной работы некоторой системы, состоящей из одного основного и двух резервных элементов, имеет гамма-распределение с параматрами у = 3 и А = 0,05. Найдите вероятность того, что система проработает не менее 5 лет.
О т в е т: Р 1Х ) 60) = е з(1+ 3 = Зз/2) и 0,42, 5. МНОГОМЕРНЫЕ СЛ’У ЧАЙНЫЕ ВЕЛИЧИНЫ В прикладных задачах обычно приходится рассматривать не одну случайную величину, а несколько случайных величин, одновременно измеряемых (наблюдаемых) в эксперименте. При этом с каждым элементпарным всходом ат е Й бывает связан набор числовых значений некоторых количественных параметров. В этой главе мы обобщим ранее полученные результаты на совокупность из нескольких случайных величин, задзвных на одном и том же веролптностпном простпранстпве. 5.1. Многомерная случайная величина.
Совместная функция распределения Определение 5.1. Совокупность случайныя величин Хт = Хт(от), …, Х„= Х„(ы), заданных на одном и том же веролтпностпном простпранстпве (Й,З,Р), называют многомерной (и-мерной) случайной величиной или тт-мерным случайным еектпором. При этом сами случайные величины Хт, Хт,, Х„называют коордннатптьнн случайного вектпора. В частности, при и = 1 говорят об одномерной, при и = 2 — двумерной с.аучайной еелнчнне (или двумерном случайном вектпоре). Для и-мерного случайного вектора воспользуемся обозначе. пнями (Хм …, Х„) и Х = (Хт, …, Х„). В случае двумерных и трехмерных случайных векторов наряду с обозначениями (Хм Хз) и (Хы Хг, Хз) будем испольэовать также обозначения (Х, У) и (Х, У, Я).

 в формуле
в формуле  нормального распределения нулевой. Кроме того, чтобы погрешность измерения по модулю не превышала 10 м, случайная погрешность должна принадлежать интервалу (-30, -10). Тогда, как следует из учебника, вероятность попадания случайной погрешности в этот интервал равна
нормального распределения нулевой. Кроме того, чтобы погрешность измерения по модулю не превышала 10 м, случайная погрешность должна принадлежать интервалу (-30, -10). Тогда, как следует из учебника, вероятность попадания случайной погрешности в этот интервал равна
 — интеграл Лапласа. А тогда, поскольку интеграл не берущийся, приходится, используя таблицы, искать методом перебора такое значение
— интеграл Лапласа. А тогда, поскольку интеграл не берущийся, приходится, используя таблицы, искать методом перебора такое значение  , при котором данная разность будет равна 0.9452. Но я не уверен, что авторы имели в виду такой метод решения. Значит, какая-то деталь в этой задаче ускользает от моего внимания.
, при котором данная разность будет равна 0.9452. Но я не уверен, что авторы имели в виду такой метод решения. Значит, какая-то деталь в этой задаче ускользает от моего внимания. метров, то высота
метров, то высота 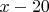 .
. , где
, где  — действительная высота, а
— действительная высота, а  и это значение не должно по модулю превышать 10, откуда и следует что
и это значение не должно по модулю превышать 10, откуда и следует что  .
. ?. Но это все равно приводит к вычислению того же интеграла (т. е. с теми же пределами). Если же при этом
?. Но это все равно приводит к вычислению того же интеграла (т. е. с теми же пределами). Если же при этом  , то вообще какая-то бессмыслица выходит. Но, даже если сделать такое предположение, то вычисления дают
, то вообще какая-то бессмыслица выходит. Но, даже если сделать такое предположение, то вычисления дают  , а в ответе — 50 метров.
, а в ответе — 50 метров.
 . Однако в условии требуется
. Однако в условии требуется  . Значит, какие-то из данных в условии не верны. В варианте задачи на приведенном выше ресурсе дано
. Значит, какие-то из данных в условии не верны. В варианте задачи на приведенном выше ресурсе дано  метров вместо
метров вместо  .
.
 , имеющейся в учебнике.
, имеющейся в учебнике.
 приведенный в учебнике ответ
приведенный в учебнике ответ  метров, то вероятность получается очень далекой от требуемой. Кроме того, авторы все-таки пишут не «случайная погрешность», а просто «погрешность», когда требуют, чтобы она была меньше
метров, то вероятность получается очень далекой от требуемой. Кроме того, авторы все-таки пишут не «случайная погрешность», а просто «погрешность», когда требуют, чтобы она была меньше